Решение рациональных уравнений методом разложения на множители

Видео:Решение квадратных уравнений. Метод разложения на множители. 8 класс.Скачать

Решение уравнений методом разложения на множители

Решение уравнений разложения на множители (метод расщепления) – это способ решения уравнений при котором мы стремимся уравнение свести их к виду:

а затем каждую скобку приравнять к нулю и решить как отдельное уравнение.

Вынесем за скобку икс.

Разобьем уравнение на два простейших.

В первом корень уравнения уже понятен, во втором надо перенести (5) в правую сторону.

Решение методом разложения на множители основывается на простой идее:

В результате умножения ноль можно получить, только если один из множителей равен нулю.

Попробуйте придумать два числа, которые при умножении дают ноль. Вы убедитесь, что хотя бы одно из них обязательно должно быть нулем.

Этот метод решения уравнений один из самых популярных, поэтому освоить его очень важно для тех, кто планирует иметь четверки и пятерки. А для освоения этого метода, конечно, надо уметь раскладывать на множители как Бог: знать все формулы сокращенного умножения, легко выносить множители за скобки, уметь применять метод группировки и т.д. Подробнее о всех способах разложения на множители смотри здесь .

Пример(задание из ОГЭ). Решите уравнение (x^3+4x^2-4x-16=0).
Решение:

Перед нами кубическое уравнение.
Применим метод группировки: из первой пары слагаемых вынесем (x^2), а из второй – минус четверку.

Видео:Дробно-рациональные уравнения. 8 класс.Скачать

Алгебра и начала математического анализа. 10 класс

Конспект урока

Алгебра и начала математического анализа, 10 класс

Урок №12. Решение алгебраических уравнений разложением на множители.

Перечень вопросов, рассматриваемых в теме

1) типы алгебраических уравнений;

2) решение алгебраические уравнения методом разложения на множители;

3) методы решения алгебраических уравнений.

Глоссарий по теме

Алгебраическое уравнение (полиномиальное уравнение) — уравнение вида P(x₁, x₂, …, x_n)=0, где P — многочлен от переменных x₁, x₂, …, x_n, которые называются неизвестными.

Коэффициенты многочлена P обычно берутся из некоторого множества F, и тогда уравнение P(x₁, x₂, …, x_n)=0 называется алгебраическим уравнение над множеством F.

Степенью алгебраического уравнения называют степень многочлена P.

Значения переменных x₁, x₂, …, x_n, которые при подстановке в алгебраическое уравнение обращают его в тождество, называются корнями этого алгебраического уравнения.

Биквадратными называются уравнения вида ах 4 + bх 2 + с = 0, где а, b, с – заданные числа, причем, а ≠ 0.

Симметрическим уравнением 3-ей степени называют уравнение вида: ax 3 + bx 2 + bx + a = 0, где a, b – заданные числа.

Уравнение вида a n x n ₊a n-1 x n-1 +…+a 1 x+a 0 =0 называется возвратным, если его коэффициенты, стоящие на симметричных позициях, равны, т.е. a n-1 =a k , при k=0, 1, …, n.

Колягин Ю.М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 10 кл. – М.: Просвещение, 2014.

Шабунин М.И., Ткачева М.В., Федорова Н.Е. Дидактические материалы Алгебра и начала математического анализа (базовый и профильный уровни) 10 кл. – М.: Просвещение, 2017.

Теоретический материал для самостоятельного изучения

Давайте вспомним, что такое алгебраическое уравнение?

Алгебраическое уравнение (полиномиальное уравнение) — уравнение вида P(x₁, x₂, …, x_n)=0, где P — многочлен от переменных x₁, x₂, …, x_n, которые называются неизвестными.

Коэффициенты многочлена P обычно берутся из некоторого поля F, и тогда уравнение P(x₁, x₂, …, x_n)=0 называется алгебраическим уравнение над полем F.

Степенью алгебраического уравнения называют степень многочлена P.

является алгебраическим уравнением седьмой степени от трёх переменных (с тремя неизвестными) над полем вещественных чисел.

Связанные определения. Значения переменных x₁, x₂, …, x_n, которые при подстановке в алгебраическое уравнение обращают его в тождество, называются корнями этого алгебраического уравнения.

Примеры и разбор решения заданий тренировочного модуля

1. Алгебраические уравнения, решаемые разложением на множители:

D(–2) : ,

Можно догадаться, что число х₁ = –1 является корнем этого уравнения, так как –1 + 3 – 2 = 0.

х + 1 = 0 или х 2 –х–2 = 0;

х₁ = –1 х_2,3 = ;

х_2,3 = ;

x 3 + х 2 – х 2 – х – 2x – 2 = 0;

(x 3 + х 2 ) – (х 2 + х) – 2(x + 1) = 0;

х 2 (х + 1) – х(х + 1) – 2(х + 1) = 0;

(х + 1) (х + 1) (х –2) = 0;

(х –2) = 0;

1. Уравнения, сводящиеся к алгебраическим
   1. Биквадратные уравнения

На прошлом уроке мы познакомились с данным видом уравнений

Определение. Биквадратными называются уравнения вида ах 4 + bх 2 + с = 0, где а, b, с – заданные числа, причем, а ≠ 0.

Метод решения

Биквадратное уравнение приводится к квадратному уравнению при помощи подстановки у=х 2 .

Новое квадратное уравнение относительно переменной у: ay 2 +by+c=0.

Решая это уравнение, мы получаем корни квадратного уравнения

Решая эти два уравнения (y₁=x₁ 2 и y₂=x₁ 2 ) относительно переменной x, мы получаем корни данного биквадратного уравнения.

Порядок действий при решении биквадратных уравнений

1. Ввести новую переменную у=х 2
2. Подставить данную переменную в исходное уравнение
3. Решить квадратное уравнение относительно новой переменной
4. После нахождения корней (y₁; y₂) подставить их в нашу переменную у=х 2 и найти исходные корни биквадратного уравнения

х 4 – 8х 2 – 9 = 0.

Решение: Пусть у = х 2 , где у 0; у 2 – 8у – 9 = 0;

По формулам Виета:

Первое решение отбрасываем ( у 0),

а из второго находим х₁ = –3; х₂ = 3.

2 Симметрические уравнения

Решение симметрических уравнений рассмотрим на примере симметрических уравнений третьей степени.

Симметрическим уравнением 3-ей степени называют уравнение вида ax 3 + bx 2 + bx + a = 0, где a, b – заданные числа.

Для того, чтобы успешно решать уравнения такого вида, полезно знать и уметь использовать следующие простейшие свойства симметрических уравнений:

1 0 . У любого симметрического уравнения нечетной степени всегда есть корень, равный -1.

Действительно, если сгруппировать в левой части слагаемые следующим образом: а(х 3 + 1) + bx(х + 1) = 0, то есть возможность вынести общий множитель, т.е.

(х + 1)(ах 2 + (b – а)x + а) = 0, поэтому,
х + 1 = 0 или ах 2 + (b – а)x + а = 0,

первое уравнение и доказывает интересующее нас утверждение.

2 0 . У симметрического уравнения корней, равных нулю, нет.

3 0 . При делении многочлена нечетной степени на (х + 1) частное является снова симметрическим многочленом.

х 3 + 2x 2 + 2х + 1 = 0.

Решение: У исходного уравнения обязательно есть корень х = –1.

Разлагая далее левую часть на множители, получим

(х + 1)(x 2 + х + 1) = 0.

x 2 + х + 1 = 0 не имеет корней.

2 Возвратные уравнения

Уравнение вида a n x n ₊a n-1 x n-1 +…+a 1 x+a 0 =0 называется возвратным, если его коэффициенты, стоящие на симметричных позициях, равны, т.е. a n-1 =a k , при k=0, 1, …, n.

Рассмотрим возвратное уравнение четвёртой степени вида

ax⁴ + bx³ + cx² + bx + a = 0, где a, b и c — некоторые числа, причём a ≠ 0. Оно является частным случаем уравнения ax⁴ + bx³ + cx² + kbx + k²a = 0 при k = 1.

Порядок действий при решении возвратных уравнений вида ax 4 + bx 3 + cx 2 + bx + a = 0:

• разделить левую и правую части уравнения на . При этом не происходит потери решения, так как x = 0 не является корнем исходного уравнения;
• группировкой привести полученное уравнение к виду

• ввести новую переменную , тогда выполнено
  , то есть ;

в новых переменных рассматриваемое уравнение является квадратным: at 2 +bt+c–2a=0;

• решить его относительно t, возвратиться к исходной переменной.

Решение: Разделим на x 2 , получим:

Введем замену:
Пусть

Видео:Как решать дробно-рациональные уравнения? | МатематикаСкачать

Рациональные уравнения

В алгебре все рациональные уравнения содержат рациональные выражения. Прежде чем дать определение, нужно выделить понятие рационального выражения.

Это не что иное, как запись, состоящая из переменного значения х и чисел, представленная с помощью арифметических действий: сложения, умножения, вычитания, деления, а также возведения в степень с натуральным показателем.

Видео:Решение уравнений с помощью разложения на множители | Алгебра 7 класс #23 | ИнфоурокСкачать

Что такое рациональные уравнения

Математики дают двоякое объяснение рациональному уравнению:

1. Если обе части уравнения представляют собой рациональные выражения, такое уравнение является рациональным.
2. Уравнение, в левой части которого рациональное выражение, а в правой стоит ноль, являются рациональным.

Например, алгебраическая запись следующего вида является рациональным уравнением:

2x − 12x 2 yz 3 = 0.

Видео:Алгебра 8. Урок 11 - Дробно-рациональные уравненияСкачать

Алгоритм решения рациональных уравнений

Чтобы решить уравнение из рассматриваемой темы, нужно сделать следующие шаги:

1. Для начала потребуется все члены уравнения переместить в одну часть.
2. Определить общий знаменатель.
3. Следующим шагом определяются множители, на которые умножаются члены равенства и выполняется преобразование этой части уравнения к алгебраической дроби.
4. Решается уравнение вида p(x) = 0.
5. Для каждого найденного корня уравнения p(x) = 0 делается проверочное действие. Если выполняется условие q(x) ≠ 0, то это значение является корнем заданного уравнения. В противном случае значение признается посторонним корнем. Оно не включается в ответ.

Рациональные уравнения являются краеугольным камнем всего курса алгебры. Человеку, научившемуся работать с подобными выражениями, умеющему упрощать, раскладывать на множители, под силу решение любой задачи, ведь преобразование выражений — это одна из составляющих частей решения серьёзного уравнения или неравенства.

Видео:Произведение многочленов. Разложение многочлена на множители способом группировки. 7 класс.Скачать

Основные алгебраические формулы

Для решения квадратных уравнений есть формулы и правила сокращённого умножения, которые начинают изучать уже в средних классах общеобразовательных школ:

1. a 2 −b 2 =(a−b)(a+b) — разность квадратов.
2. (a+b) 2 =a 2 +2ab+b 2 — квадрат суммы.
3. (a−b) 2 =a 2 −2ab+b 2 — квадрат разности.
4. a 3 +b 3 =(a+b)(a2−ab+b2) — сумма кубов.
5. a 3 −b 3 =(a−b)(a 2 +ab+b 2 ) — разность кубов.

Видео:Разложение квадратного трехчлена на множители. 8 класс.Скачать

Преобразования, упрощающие решение рациональных уравнений

Преобразования равносильны, если получается новое уравнение, причем корни будут такими же, как в изначальном выражении.

Деление или умножение уравнения на любое, отличное от нуля число, является равносильным преобразованием. Перенос параметров уравнения через знак равенства в ту или иную часть — тоже тождественное преобразование.

Видео:Решение дробных рациональных уравнений. Алгебра, 8 классСкачать

Примеры решений уравнений с дробями

Алгоритм решения следующий: все части приводятся к общему знаменателю. Но после того, как найдены корни при использовании неравносильных преобразований, они проверяются методом подстановки в уравнение.

Приведем дробь к такому виду:

С учетом всего этого получится выражение:

Видео:Решение уравнений с помощью разложения на множители.Скачать

Методы решения

Наиболее часто используемые способы для решения уравнений со степенями:

• метод замены переменной;
• разложение на множители.

Биквадратные уравнения типа ax 4 + bx 2 + c = 0 решаются методом замены множителя: x 2 = y.

Системы линейных уравнений также решаются методом замены.

К примеру, требуется решить систему линейных уравнений:

Принцип решения сводится к тому, что надо избавиться от лишней переменной:

Далее уравнение решается просто.

Видео:РАЗЛОЖЕНИЕ НА МНОЖИТЕЛИ / Алгебра 7 классСкачать

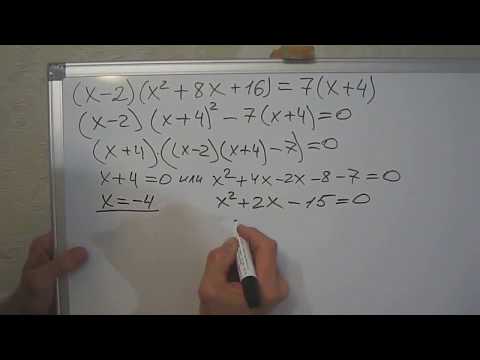
Пример решения с разложением на множители

Любые сложные вычисления нужно выполнять по действиям. Так проще избавиться от ненужных ошибок.

Алгоритм решения такой: вначале выполняется действие, заключённое в скобках, затем выполняется то, что записано во второй скобке и так далее. В конце все части объединяются, и находится результат.

Для самостоятельной работы при решении рациональных уравнений можно использовать онлайн-калькулятор. Он помогает лучше усвоить некоторые методы решения и быстрее справиться с заданиями.

📺 Видео

Разложение кубических выражений на множителиСкачать

2.1. Рациональные уравнения. Разложение на множители.Скачать

Решение уравнений методом разложения на множителиСкачать

3.1. Системы рациональных уравнений. Метод сложения, подстановки и разложения на множителиСкачать

Разложение на множители. 7 класс. Вебинар | МатематикаСкачать

Математика| Разложение квадратного трехчлена на множители.Скачать

ЭТО НУЖНО ЗНАТЬ — Как решать Дробно Рациональные уравнения?Скачать

Решение задач с помощью рациональных уравнений. Алгебра, 8 классСкачать

Алгебра 10 класс (Урок№12 - Решение алгебраических уравнений разложением на множители.)Скачать

Решение Тригонометрических Уравнений Методом Разложения На Множители. 10 классСкачать