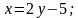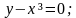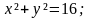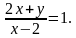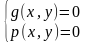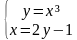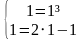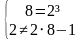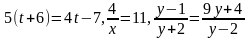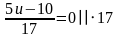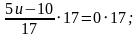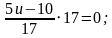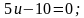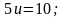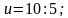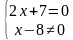Решение рациональных иррациональных показательных тригонометрических уравнений и их систем

Видео:СУПЕР ЛАЙФХАК — Как решать Иррациональные УравненияСкачать

Уравнения и системы уравнений. Рациональные, иррациональные, показательные и тригонометрические уравнения и системы. Равносильность уравнений, неравенств, систем.
презентация к уроку по алгебре (10, 11 класс)

Уравнения и системы уравнений. Рациональные, иррациональные, показательные и тригонометрические уравнения и системы. Равносильность уравнений, неравенств, систем.

Видео:Как решают уравнения в России и СШАСкачать

Скачать:

Видео:Иррациональные уравнения и их системы. 11 класс.Скачать

Предварительный просмотр:

Тема: Уравнения и системы уравнений. Рациональные, иррациональные, показательные и тригонометрические уравнения и системы. Равносильность уравнений, неравенств, систем.

Рассмотреть способы решения рациональных, иррациональных, показательных и тригонометрических уравнений и неравенств.

1. Ознакомьтесь с алгебраическими системами уравнений по ссылке:

1. Ознакомьтесь со способами решения показательных уравнений и систем уравнений

1. Ознакомьтесь со способами решения иррациональных уравнений

1. Ознакомьтесь со способами решения тригонометрических уравнений

1. Ознакомьтесь со способами решения систем уравнений

1. Ознакомьтесь со способами решения систем тригонометрических уравнений

1. Решите графически систему уравнений

1. Решите систему уравнений:

а) б)

1. Площадь прямоугольника равна 36см 2 , а его периметр – 24см. Найдите стороны прямоугольника.

4. Постройте график уравнения (3х+2)(у+х 2 -4)=0

5. Решите систему уравнений

Видео:Решение тригонометрических уравнений. Подготовка к ЕГЭ | Математика TutorOnlineСкачать

По теме: методические разработки, презентации и конспекты

Урок-зачет в 10 классе по теме «Тригонометрические уравнения, неравенства, системы уравнений»

Цель урока: Проверить знания и умение применений формул для решения тригонометрических уравнений.Вид работы: «Смотр знаний», состоящий из 5 этапов, проводится в течение двух уроков. За каждый эт.

Конспект урока по теме: ”Тригонометрические уравнения. Решение простейших тригонометрических уравнений вида sinx = a. “

Разобраны свойства функции sinx. Приведено решение уравнения sinx=a. Разобраны 4 примера.

Тема 17. ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ. Решение простейших тригонометрических уравнений. Общий приём. Метод разложения на множители.

Уважаемые коллеги!Актуальной задачей на сегодняшний день является качественная подготовка учащихся к единому государственному экзамену (ЕГЭ) по математике, а также абитуриентов к вступительным э.

Тест по темам « Решение уравнений и их систем», «Решение неравенств и их систем» и «Решение уравнений, неравенств, систем неравенств с модулем».

Задания теста соответствуют содержанию учебника «Алгебра. 9 класс : учеб. для учащихся общеобразовательных учреждений / Ю. Н. Макарычев , Н. Г. Миндюк , К. И. Нешков , И. Е. Феоктист.

Урок-лекция по алгебре и началам анализа «Решение тригонометрических уравнений, неравенств и систем уравнений»

В данной лекции подробно указаны все способы решения тригонометрических уравнений, неравенств и систем уравнений.

Урок-зачет по теории и практике по теме «Тригонометрические уравнения, неравенства и системы уравнений»

В данном уроке представлены вопросы к зачету и практические задания.

Системы уравнений с двумя переменными. Графический метод решения систем двух линейных уравнений с двумя переменными

Урок объяснения нового материала по учебнику «Алгебра, 7 класс» А.Г. Мерзляк, параграф 26. Презентация составлена для объяснения новой темы в Zoom при дистанционном обучении.

Видео:ПРОСТЕЙШИЙ способ решения Показательных УравненийСкачать

Решение рациональных, иррациональных, показательных, тригонометрических и логарифмических уравнений и систем

Опубликовано 16.09.2020Подготовка к ЕГЭ

Видео:10 класс, 23 урок, Методы решения тригонометрических уравненийСкачать

Решение рациональных, иррациональных, показательных, тригонометрических и логарифмических уравнений и систем

На сегодняшний день ЕГЭ по математике проходит в форме решения заданий, содержащихся в контрольно-измерительных материалах, при этом, ответы на задания выносят на отдельный бланк.

Уравнения могут быть следующих видов:

В данной статье рассмотрена профильная математика, а именно раздел по видам и системам рациональных, иррациональных, показательных, тригонометрических и логарифмических уравнений.

При решении уравнений нужно помнить основные термины:

— Корнем уравнения называют неизвестное число, которое нужно найти;

— Решение уравнения предполагает нахождение его корня;

— Уравнения, у которых совпадают решения называют равносильными;

— ОДЗ – область допустимых значений;

— Если возможно заменить переменные, то нужно это выполнить;

— После решения уравнения необходимо провести проверку на правильность нахождения корня.

Итак, рассмотрим каждый вид уравнений по отдельности, включая примеры решения.

1. Рациональные уравнения – уравнения, у которых, как правило, слева расположено рациональное выражение, а справа – ноль.

Рациональным уравнением называют уравнение вида r(х)=0.

Если обе части уравнения являются рациональными выражениями, то рациональные уравнения называют целыми.

Дробно-рациональным называют уравнение, которое содержит дробное выражение.

Порядок действий при решении данного вида уравнения должен быть следующий:

— Все члены должны быть переведены в левую часть уравнения;

— Данную часть уравнения нужно представить в виде дроби p(x)/q(x);

— Для полученного решения нужно провести проверку, то есть.

При решение этого рационального уравнения понадобится формула (а-в)2=а2-2ав+в2.

Рассмотрим ещё один пример решения рационального уравнения:

На основе примеров показано, что рациональные уравнения могут быть с разным количеством переменных.

Иррациональными уравнениями считают уравнения с переменной под корнем. Для того, чтобы определить является ли уравнение иррациональным нужно просто посмотреть на корень переменной. Следует учитывать, что в некоторых учебниках по математике иррациональное уравнение определяют другим способом.

Способы решения таких уравнений:

— Возвести в степень обе части уравнения;

— Ввести новые переменные;

Пример решения уравнения по первому способу:

Пример решения по второму способу:

1. Показательные уравнения

Показательные уравнения – уравнение, содержащее неизвестный показатель.

В учебниках по математике разных авторов определение показательного уравнения может отличаться. Обычно такие отличия касаются незначительных деталей.

Как правило, это уравнения вида af(x)=ag(x), где а не равно одному и число а больше нуля. Из этого следует, что f(x)=g(x).

— Уравнение с одним основанием;

— Уравнение с равными основаниями.

Существует следующие способы решения таких уравнений:

— Использовать метод логарифмов;

— Привести уравнение к квадратному виду;

— Вынести за скобку общий множитель;

— Ввести новую переменную.

Итак, как решить показательное уравнение? Любое по сложности уравнение нужно привести в простую форму.

Рассмотрим наиболее простой пример решения показательного уравнения:

Для решения данного уравнения следует 2 возвести во вторую степень.

Решение даже простейших показательных уравнений имеет большую значимость. Поэтому далее вам будет легче решать уравнения более сложного уровня.

Данная тема является одной из самых сложных, поэтому следует внимательно подойти к изучению данной темы. Известны три формулы тригонометрических уравнений, запомнить которые не составляет особой сложности.

Наиболее простое тригонометрическое уравнение имеет вид sin x=a, cos x=a, tg x=а, а – число действительное.

Способы решения таких уравнений:

— Решение с помощью форму и приведение к простейшему;

— Ввод других переменных;

— Разложить уравнение по множителям.

Пример решения тригонометрического уравнения:

Здесь нужно рисовать окружность, далее выделить точки с координатой ½, соответственно, это точки 5п/6 и п/6. Если пройти по окружности, исходя из данных точек, то х=п/6+2пk, x=5п/6+2пn. При этом синус и косинус принадлежат промежутку [-1;1]. Если при решении уравнения в его правой части стоит число не принадлежащее промежутку, считается, что уравнение не имеет решения.

Также рассмотрим пример решения уравнения, разложив его по множителям.

Нужно применить формулу sin2x = 2sinxcosx.

2sinxcosx – sinx = 0.

sinx (2cosx – 1) = 0.

Таким образом, если один из множителей равен нулю, то решение уравнения также равно нулю.

Далее, sinx=0, x=пk.

1. Логарифмические уравнения

Особое значение имеет подготовка ЕГЭ по математике логарифмы, это обусловлено тем, что в КИМах чаще всего встречаются именно этого вида уравнения.

Логарифмическое уравнение – это уравнение с неизвестной величиной, находящейся внутри логарифма.

Примерами логарифмических уравнений являются уравнения следующего вида:

Способы решения уравнений данного вида:

— Применять способ уравнивания к единице;

— Применять способ умножать на единицу;

— Применять доступные правила логарифмов;

— Введение другого основания;

— Возвести в степень.

Самым простым логарифмическим уравнением принято считать уравнение вида log a x = b, при этом основание a>0,a≠1.

Пример решения уравнения:

Сначала следует найти значение области, то есть ОДЗ. При этом нужно помнить, что под логарифмом выражение всегда положительное. Воспользуемся логарифмическим определением, представим х степью основания 2 логарифма, степень будет равна 3.

Решение уравнения является ОДЗ, то есть корень уравнения найден.

Таким образом, подобное задание ЕГЭ по математике легко можно решить, зная логарифмы и способы их решения.

Оставить Комментарий Отменить ответ

Для отправки комментария вам необходимо авторизоваться.

Видео:Удалили с экзамена ОГЭ Устное Собеседование shorts #shortsСкачать

Выбери тему

Видео:Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать

Самые популярные записи

• Наука. Основные особенности научного мышления. Естественные и социально гуманитарные науки (3 981)
• Строение растения. Стебель, лист и цветок. (3 201)
• Свобода и необходимость в человеческой деятельности. Свобода и ответственность. (2 851)
• ЕГЭ по обществознанию: мышление и деятельность; потребности и интересы (2 819)

Видео:Задание 5Скачать

StudyWay

Видео:СЛОЖИТЕ ДВА КОРНЯСкачать

Помощь

© 2022 StudyWay. Все права защищены.

Заполни анкету и с тобой свяжется наш менеджер 👍

КУРС «ЧЕЛОВЕК И ОБЩЕСТВО»

КУРС «ЭКОНОМИКА»

КУРС «СОЦИОЛОГИЯ»

КУРС «ПОЛИТИКА»

КУРС «ПРАВО»

Куратор поможет тебе разобраться со всеми темами,
проверит домашки и поддержит.

Занятия строятся самостоятельно.
Открывается доступ ко всем записанным занятиям и курсам.

Ты можешь попробовать 3 наших закрытых занятия из курса «Прорыв».

Записаться можно через Instagram

Для этого напиши в Direct (в личку) кодовое слово «Пробный«

Видео:Решение тригонометрических уравнений и их систем. 10 класс.Скачать

Что за курс и что тебя там будет ждать?

12 мощнейших онлайн занятий по 2 часа в формате вебинаров.
Содержание вебинара: повторение предыдущей темы, теория, перерыв и практика.

Воркбук (рабочая тетрадь)абсолютно к каждому уроку со всей необходимой теорией к этой теме и практикой.

Личный куратор — это твой помощник во всех учебных вопросах.
Они занимаются проверкой твоих домашних заданий, поддерживают и мотивируют двигаться дальше, даже когда хочется сдаться.

На собственной онлайн платформе тебя ждут
Домашние задания, которые необходимо решать после каждого занятия.
Все задания построены на базе создателей ЕГЭ — Котова / Лискова.

К каждому тестовому вопросу будет подробный разбор от главного куратора.
А задания, где необходимо оценить ответ (вторая часть) — будет проверять твой личный куратор и писать подробный комментарий про ошибки

Общий чат единомышленников, поделенный на команды.
Название даете совместно (например «Воробушки»)

Ты будешь двигаться сообща с однокурсниками, поддерживая и мотивируя друг друга.
За лучшую командную успеваемость всей команде будут выделены призы в конце каждого месяца (скидка на обучение, стикерпаки и т.д).

Личный помощник — это твой верный друг и помощник, который поможет тебе со всеми техническими вопросами, ответит на вопросы про поступление, да и просто может обсудить какие-то личные вопросы, поделиться переживаниями.

Доступ к уникальной «Академии косатиков».

Там ты сможешь найти:
Банк теории, банк планов, банк аргументов, курсы по работе со всей второй частью, термины, курсы по саморазвитию, полезные лайфхаки и всю подробную информация о ЕГЭ.

Игровая система на нашей платформе StudyWay👇

За выполнение заданий получаешь баллы (XP).

При достижении нового уровня у тебя открываются новые персонажи из Marvel, DC Comics, Игра престолов и Star Wars, а также на каждом новом уровне тебя ждут призы от нашей школы.

Основная ценность курса
1. Изучение теории и практики с учетом изменений в ЕГЭ 2022
2. Заложение фундамента и основы предмета
3. Прохождение всей теории для первой части
4. Нарешивание всех возможных типов заданий
5. Повышение результата с 0 до 60 баллов

Отличия тарифа «Стандарт от «Профи».

Дополнительные домашние задания
необходимо выполнять. Это значительно повысит твою успеваемость и улучшит показатели.

Дополнительное объяснение
твой личный куратор объяснит тебе тему повторно, если останется что-то не понятным

Групповые зачеты
у тебя будут зачеты с твоим личным куратором в мини группах по 5 человек. Там спрашиваются пройденные темы, термины и так далее.

Карта памяти
будешь восполнять все пройденные в удобной интеллект карте и в конце учебы у тебя выйдет файл с полноценной теорией по всем темам и разделам.

Персональный звонок куратору
1 раз в месяц ты можешь позвонить своему куратору и обсудить все волнующие тебя вопросы в течении 20 минут.

Секретный квест
1 раз в месяц ты будешь созваниваться с другим учеником курса и проводить совместные зачеты, тем самым познакомишься с новыми ребятами из других городов, уберешь страхи знакомства, повторишь и закрепишь пройденные темы.

Видео:Показательные уравнения. 11 класс.Скачать

Рациональные и иррациональные уравнения и системы уравнений

РАЦИОНАЛЬНЫЕ И ИРРАЦИОНАЛЬНЫЕ УРАВНЕНИЯ И СИСТЕМЫ УРАВНЕНИЙ.

(Раздел «Уравнения и неравенства»)

ДЕЯТЕЛЬНОСТНАЯ КАРТА УЧЕБНОГО ЗАНЯТИЯ

Просмотр содержимого документа
«Рациональные и иррациональные уравнения и системы уравнений»

(Раздел «Уравнения и неравенства»)

ДЕЯТЕЛЬНОСТНАЯ КАРТА УЧЕБНОГО ЗАНЯТИЯ

Профессии: 15.01.20 Слесарь по контрольно-измерительным приборам и автоматике, 09.01.03 Мастер по обработке цифровой информации, 23.01.03 Автомеханик, 09.01.01 Наладчик аппаратного и программного обеспечения

Учебные группы: КИП-11, М-11, А-11, Н-11

Учебная дисциплина: ООПу.04 Математика

Тема учебного занятия: Рациональные и иррациональные уравнения и системы уравнений.

Тип урока: урок «открытия» новых знаний

Вид урока: лекция-беседа

технические: мультимедийный проектор, персональный компьютер;

информационно-коммуникационные: электронная презентация.

методическая: использование объяснительно-иллюстративного метода обучения с целью формирования математического мышления студентов;

образовательная: создание условий для овладения знаниями о рациональных и иррациональных уравнениях и систем уравнений;

развивающая: развитие умений планировать, анализировать, выдвигать гипотезы по решению заданий, применять полученные знания для выполнения упражнений;

воспитательная: воспитание интереса к изучению математики, математической культуры студентов.

сформированность знаний о рациональных и иррациональных уравнениях и систем уравнений;

владение умением решать задачи на рациональные и иррациональные уравнения и системы уравнений;

умение ставить перед собой цель, видеть ожидаемый результат работы;

умение рационально распределять рабочее время;

умение объективно оценивать свои возможности, анализировать свои результаты, корректировать свои действия;

владение навыками познавательной рефлексии;

умение осуществлять поиск и отбор необходимой информации;

умение сопоставлять и анализировать, выделять в тексте базовые и вспомогательные концепты, опорные понятия, тезисы, структурировать их взаимосвязь;

умение структурировать полученную информацию;

умение анализировать и обобщать информацию;

умение продуктивно общаться и взаимодействовать в процессе совместной деятельности, учитывать позиции других участников деятельности;

умение выражать свои мысли с достаточной полнотой и точностью.

Образовательные технологии: традиционное обучение.

Формы организации обучения: фронтальная, индивидуальная.

Методы обучения и контроля:

практические: метод сравнения, метод анализа и структурирования.

методы контроля и самоконтроля: устный контроль, самоконтроль.

Федеральный государственный образовательный стандарт среднего общего образования (утв. приказом Министерства образования и науки Российской Федерации (Минобрнауки России) от 17 мая 2012 г. № 413 г.). – М.: Министерство образования и науки РФ, – 2012.

Башмаков М. И. Математика: учебник для студ. учреждений сред. проф. образования. − М.: Издательский центр «Академия», 2018. – 256 с.

Башмаков М. И. Математика. Сборник задач профильной направленности: учеб. пособие для студ. учреждений сред. проф. образования. − М.: Издательский центр «Академия», 2014. – 416 с.

Алимов Ш.А., Колягин Ю.М. Алгебра и начала математического анализа (базовый и углубленный уровни).10—11 классы. Учебник. − М.: Просвещение, 2014. – 464 с.

Атанасян Л.С. Геометрия. 10 − 11 классы: учебник для общеобразовательных учреждений: базовый и профильный уровни / Атанасян Л.С., Бутузов В.Ф. и др. – М.: Просвещение, 2013. – 255 с.

Богомолов Н.В. Практические занятия по математике: Учеб. пособие для техникумов / Н.В. Богомолов. – М.: Высш. шк., 2013. – 495 с.

Колягин Ю.М., Луканкин Г.Л., Яковлев Г.Н. Математика (Книга 1): Учебное пособие. – М.: Издательство «Новая волна», 2013. – 656 с.

Колягин Ю.М., Луканкин Г.Л., Яковлев Г.Н. Математика (Книга 2): Учебное пособие. – М.: Издательство «Новая волна», 2013. – 592 с.

Никольский С.М. Алгебра и начала анализа: учебник для 10 класса общеобразоват. учреждений: базовый и профильный уровни / С.М. Никольский, М.К. Потапов. – М.: Просвещение, 2013. – 430 с.

Никольский С.М. Алгебра и начала анализа: учебник для 11 класса общеобразоват. учреждений: базовый и профильный уровни / С.М. Никольский, М.К. Потапов. – М.: Просвещение, 2013. – 464 с.

Федеральный центр информационно-образовательных ресурсов [Электронный ресурс] URL: www. fcior. edu. ru

Единая коллекции цифровых образовательных ресурсов [Электронный ресурс] URL: www. school-collection. edu. ru

Инновационные педагогические технологии: учебное пособие/ Михелькевич В.Н., Нестеренко В.М., Кравцова П.Г. – Самар. гос. тех. ун-т Самара, 2001. – 89 с.

Кульневич С.В., Лакоценина Т.П. Современный урок. Часть 1: Научно-практич. пособие для учителей, методистов, руководителей учебных заведений, студентов пед. заведений, слушателей ИПК. – Ростов н/Д: Учитель, 2005. – 288 с.

Кульневич С.В., Лакоценина Т.П. Современный урок. Часть 3: Научно-практич. пособие для учителей, методистов, руководителей учебных заведений, студентов пед. заведений, слушателей ИПК. – Ростов н/Д: Учитель, 2007. – 288 с.

Махмутов М.И. Проблемное обучение: Основные вопросы теории. – М.: Педагогика, 1975. – 368 с.

Основные термины и понятия: рациональные уравнения, иррациональные уравнения, рациональные системы уравнения, иррациональные системы уравнения.

ПЛАН УЧЕБНОГО ЗАНЯТИЯ

Содержание учебного материала:

1) Сформированность знаний о рациональных и иррациональных уравнениях и систем уравнений.

2) Закрепление теоретического материала по теме с помощью решения упражнений.

Этап мотивации (самоопределения) к учебной деятельности (2 мин)

Преподаватель приветствует студентов, создает деловую обстановку, настраивает на продуктивную мыслительную деятельность.

Этап актуализации опорных знаний. Целеполагание (15 мин)

Преподаватель задает вопросы студентам:

Что такое рациональное уравнение?

Что такое иррациональное уравнение?

Студенты отвечают на эти вопросы, вспоминая знания, полученные на предыдущем занятии.

Формулирование темы и целей учебного занятия.

Работа над новой темой («открытие» нового знания) (48 мин)

Алгоритм работы над «открытием» нового знания:

Формулирование преподавателем определений рациональных и иррациональных уравнений и систем уравнений.

Рациональным уравнением с двумя переменными 𝑥 и 𝑦 называют

уравнение вида 𝑔(𝑥,𝑦)=0, где 𝑔(𝑥,𝑦) — рациональное выражение.

Примеры рациональных уравнений с двумя переменными 𝑥 и 𝑦.

Решением уравнения 𝑔(𝑥,𝑦)=0 называют такую пару чисел (𝑥;𝑦),

которая обращает равенство 𝑔(𝑥,𝑦)=0 в верное числовое равенство.

Если поставлена задача найти пары чисел (𝑥;𝑦), которые одновременно удовлетворяют уравнению 𝑔(𝑥,𝑦)=0 и уравнению 𝑝(𝑥, 𝑦) = 0, то говорят, что уравнения 𝑔(𝑥,𝑦)=0 и 𝑝(𝑥, 𝑦) = 0 образуют систему уравнений:

Пару значений (𝑥;𝑦), которая одновременно является решением и первого, и второго

уравнений системы, называют решением системы уравнений.

Решить систему уравнений — это значит найти все её решения или установить, что решений нет.

a) Пара чисел (1;1) является решением системы уравнений, т. к.

обращает каждое уравнение системы в верное числовое равенство.

б) Пара чисел (2;8) не является решением системы уравнений, т. к.

только первое уравнение системы обращает в верное числовое равенство.

Уравнения, в которых под знаком корня содержится переменная, называются иррациональными.

Решение иррациональных уравнений обычно сводится к переходу от иррационального к рациональному уравнению путём возведения в степень 𝑛 обеих частей уравнения.

При решении иррациональных уравнений необходимо учитывать следующее:
1. если показатель корня — чётное число, то подкоренное выражение и значение корня не должны быть отрицательными;

2. если показатель корня — нечётное число, то подкоренное выражение может быть любым действительным числом;

3. при возведении обеих частей уравнения в чётную степень могут возникать посторонние корни, поэтому при использовании данного метода необходимо делать проверку или находить область допустимых значений.

Включение нового знания в систему имеющихся знаний (20 мин)

Среди рациональных уравнений

5(𝑡+6)=4𝑡−7 является целым уравнением,

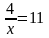
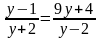
а , — дробные рациональные уравнения.

Чтобы решить дробное рациональное уравнение, надо:

— перенести все слагаемые из правой части в левую (если необходимо), поменяв знаки на противоположные;
— привести дроби к общему знаменателю;
— заменить данное уравнение целым, умножив обе его части на общий знаменатель;

— решить получившееся целое уравнение;

— исключить корни, которые обращают в нуль общий знаменатель.

Дробь обращается в нуль лишь при условиях, что числитель равен нулю, а знаменатель отличен от нуля.

1) решить уравнение .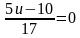
Решение. Умножим обе части уравнения на знаменатель и

решим линейное уравнение:

Ответ: 𝑢=2.

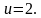
2) Решить уравнение .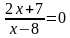
Решение. Дробь обращается в нуль лишь при условиях, что числитель равен нулю,

а знаменатель отличен от нуля. Значит, получаем

Поскольку при 𝑥=−3,5 знаменатель не обращается в нуль, то это значение является корнем уравнения.
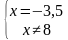
Ответ: 𝑥=−3,5.

Пример иррациональных уравнений:

1. решить уравнение .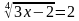

Возведём обе части уравнения в четвёртую степень:

2. Решить уравнение .

Решение: возведём обе части уравнения в квадрат:

Полученное неполное квадратное уравнение имеет два корня: −5 и 5.
Произведём проверку полученных корней, для этого подставим значения переменной 𝑥 в исходное уравнение.

Проверка
При — верно.
При — верно.
Значит, исходное иррациональное уравнение имеет два корня.
Ответ: −5 и 5.

3. Решить уравнение .

Решение: уравнение не имеет корней. Корень чётной степени — неотрицательное число.

Решение: возведём обе части уравнения в куб:

Рефлексия. Подведение итогов учебного занятия (5 мин)

Беседа со студентами по содержанию занятия. Вопросы для беседы:

Какая была тема сегодняшнего занятия?

Что нового вы узнали?

Какая была цель занятия?

Что получилось у вас сегодня?

Что не получилось?

Достигли ли мы поставленной цели?

Инструктирование о выполнении домашнего задания

🌟 Видео

Математика это не ИсламСкачать

ЧТО НАДО ГОВОРИТЬ ЕСЛИ НЕ СДЕЛАЛ ДОМАШКУ!Скачать

«Иррациональное уравнение» #умскул #math #умскул_профильнаяматематика #аделияадамова #mathematicsСкачать

Иррациональные уравнения и их системы. Практическая часть. 1ч. 11 класс.Скачать

8 класс, 38 урок, Иррациональные уравненияСкачать

Как решать неравенства? Математика 10 класс | TutorOnlineСкачать

Дробно-рациональные уравнения. 8 класс.Скачать

Система иррациональных уравнений #3Скачать