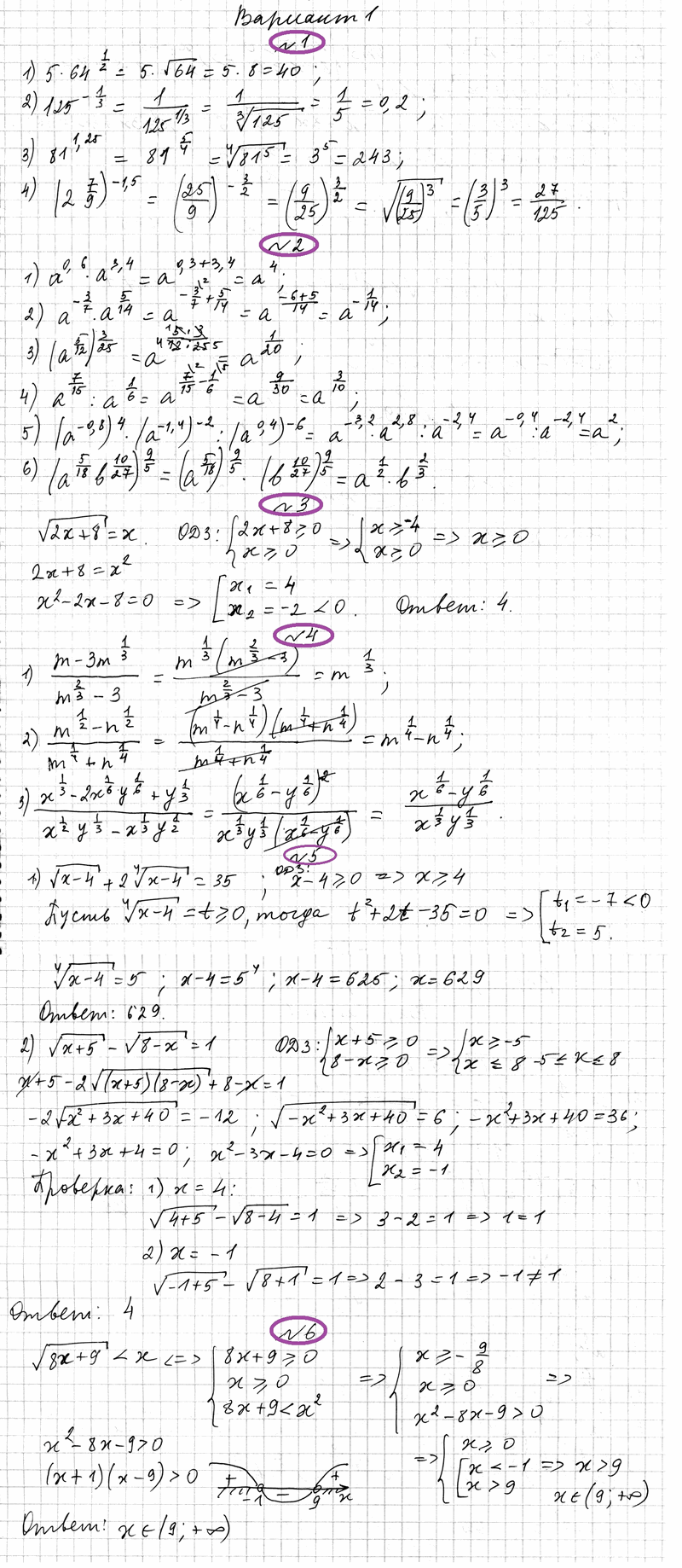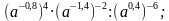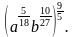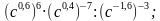Решение рациональных и иррациональных уравнений и неравенств вариант 1

Алгебра. Мерзляк 10 класс Контрольная 3 в четырех вариантах. Контрольная работа по алгебре в 10 классе «Степень с рациональным показателем и её свойства. Иррациональные уравнения и неравенства» для УМК Мерзляк, Полонский, Якир (базовый уровень). Транскрипт заданий. Решения и ответы только на 2 варианта (для родителей).

Алгебра 10 класс (УМК Мерзляк)
Контрольная работа № 3

Тема: Степень с рациональным показателем и её свойства.
Иррациональные уравнения и неравенства

Проверяемые темы (параграфы) учебника: 10) Определение и свойства степени с рациональным показателем. 11) Иррациональные уравнения. 12) Метод равносильных преобразований для решения иррациональных уравнений. 13) Иррациональные неравенства.

Вариант 1

1. Найдите значение выражения:
   1) 5 • 64 1/2 ; 2) 125 –1/3 ; 3) 81 1,25 ; 4) (2 7 /₉) –1,5 .
2. Упростите выражение: 1) а 0,6 • а 3,4 ; 2) а –3/7 а 5/14 ; 3) (a 5/12 ) 3/25 ; 4) а 7/15 : а 1/6 ; 5) (a –0,8 ) 4 • (a –1,4 ) –2 : (a 0,4 ) –6 ; 6) (a 5/18 b 10/27 ) 9/5 .
3. Решите уравнение √[2х + 8] = х.
4. Сократите дробь: 1) (m – 3m 1/3 )/(m 2/3 – 3); 2) (m 1/2 – n 1/2 )/(m 1/4 + n 1/4 ); 3) (x 1/3 – 2x 1/6 y 1/6 + y 1/3 ) / (x 1/2 y 1/3 – x 1/3 y 1/2 ).
5. Решите уравнение: 1) √[х – 4] + 2 4 √[х – 4] = 35; 2) √[х + 5] – √[8 – х] = 1.
6. Решите неравенство √[8х + 9] ОТВЕТЫ на контрольную работу

Ответы на КР-3 Вариант 1

Ответы на КР-3 Вариант 2

Вы смотрели: Алгебра. Мерзляк 10 класс Контрольная 3 в 4-х вариантах. Контрольная работа по математике в 10 классе «Степень с рациональным показателем и её свойства. Иррациональные уравнения и неравенства» по УМК Мерзляк, Полонский, Якир. Транскрипт заданий. Решения и ответы только на 2 варианта (для родителей).

(с) Цитаты из пособия «Алгебра 10 класс. Методическое пособие / Е.В. Буцко и др.» использованы в учебных целях.

Добавить комментарий Отменить ответ

Этот сайт использует Akismet для борьбы со спамом. Узнайте, как обрабатываются ваши данные комментариев.

Видео:Алгебра 10 класс (Урок№20 - Иррациональные уравнения и неравенства.)Скачать

Предметы

Видео:Подготовка к ОГЭ . Рациональные неравенства | Математика | TutorOnlineСкачать

Новые работы

Видео:СУПЕР ЛАЙФХАК — Как решать Иррациональные УравненияСкачать

Найти контрольную:

Видео:Как решать неравенства? Математика 10 класс | TutorOnlineСкачать

Авторы работ и УМК

Видео:Рациональные уравнения. ОГЭ номер 21 | ЕГЭ номер 13 | Математика | TutorOnlineСкачать

Предметы

Видео:Иррациональные неравенства | Математика ЕГЭ | УмскулСкачать

Важные страницы

Соглашение о конфиденциальности

(с) 2020-2022. Дистанционный информационный Центр НПИ (г.Москва). Бесплатная помощь школьникам, находящимся на домашнем или семейном обучении. Цитаты из учебных пособий размещены в учебных целях. Контакты: kip1979@mail.ru

Видео:Иррациональные уравнения и их системы. 11 класс.Скачать

Популярное

Видео:ИРРАЦИОНАЛЬНЫЕ НЕРАВЕНСТВА неравенства с корнемСкачать

Предупреждение

Продолжая использовать наш сайт, вы даете согласие на обработку файлов cookie, пользовательских данных (сведения о местоположении; тип и версия ОС; тип и версия Браузера; тип устройства и разрешение его экрана; источник откуда пришел на сайт пользователь; с какого сайта или по какой рекламе; язык ОС и Браузера; какие страницы открывает и на какие кнопки нажимает пользователь; ip-адрес) в целях функционирования сайта, проведения ретаргетинга и проведения статистических исследований и обзоров. Если вы не хотите, чтобы ваши данные обрабатывались, покиньте сайт.

Видео:Как решать дробно-рациональные уравнения? | МатематикаСкачать

Контрольная работа № 3 по теме «Степень с рациональным показателем и её свойства. Иррациональные уравнения и неравенства» (10 класс, Мерзляк А.Г. и др.)

Даны четыре варианта контрольной работы, удобно вносить изменения и печатать.

Просмотр содержимого документа
«Контрольная работа № 3 по теме «Степень с рациональным показателем и её свойства. Иррациональные уравнения и неравенства» (10 класс, Мерзляк А.Г. и др.)»

Контрольная работа № 3 по теме «Степень с рациональным показателем и её свойства. Иррациональные уравнения и неравенства»

1. Найдите значение выражения:

1) ; 2) ; 3) ; 4) .

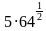
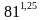
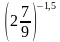
2. Упростите выражение:

1) ; 3) ; 5)

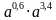
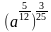
2) ; 4) 6)

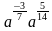
3. Решите уравнение .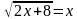

4. Сократите дробь:

1) ; 2) ; 3) .

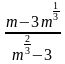
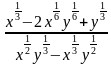
5. Решите уравнение:

1) ; 2) .

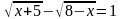
6. Решите неравенство .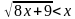

1. Найдите значение выражения:

1) ; 2) ; 3) ; 4) .

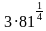
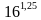
2. Упростите выражение:

1) ; 3) ; 5)

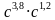
2) ; 4) 6)

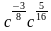
Видео:8 класс, 38 урок, Иррациональные уравненияСкачать

Урок «Решение рациональных, иррациональных уравнений и систем»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Рабочие листы и материалы для учителей и воспитателей

Более 300 дидактических материалов для школьного и домашнего обучения

Тема урока : « Решение рациональных, иррациональных уравнений и систем ».

закрепить основные способы решения рациональных и иррациональных уравнений и систем;

Повторить некоторые приемы решения рациональных и иррациональных уравнений;

формировать приемы логического мышления;

развивать умения анализировать, умения работать с информацией, представленной в различных формах;

развивать коммуникативные умения;

развивать интерес к предмету.

воспитание коммуникативной и информационной культуры студентов;

эстетическое воспитание осуществляется через формирование умения рационально, аккуратно оформлять задание на доске и в тетради.

Вид урока: комбинированный, с работой на ИД, частично – поисковый.

Тип урока: урок совершенствования умений и навыков .

Технологии обучения: информационно – коммуникационная, здоровье сберегающая, коллективная.

ноутбук, интерактивная доска, проектор, презентация.

презентация к учебному занятию в PowerPoint ««Уравнения, неравенства и системы»;электронные ресурсы;

Башмаков М.И. Математика. Учебник для НПО и СПО . Мордкович А.Г. Алгебра и начала математического анализа (профильный уровень). 11. В 2ч. Ч.1. Учебник и задачник.

чертежные принадлежности, тетради студентов.

1.Актуализация ранее усвоенных знаний:

1.1. Проверка домашнего задания ( фронтальная проверка, выборочно проверить в тетрадях ) .

1.2.Фронтальный опрос: по теме «Рациональные и иррациональные уравнения» . Повторить алгоритм решения рациональных и иррациональных уравнений, и их систем, основные методы решения, изучаемые ранее.

Рациональное выражение – это алгебраическое выражение, составленное из чисел и переменной x с помощью операций сложения, вычитания, умножения, деления и возведения в степень с натуральным показателем. Ну а рациональное уравнение – это равенство двух рациональных выражений.

Дробно рациональные уравнения — рациональные (без знака корня) уравнения, в которых левая или правая части являются дробными выражениями.

Какие уравнения называются иррациональными? ( Иррациональными называются уравнения, содержащие переменную под знаком радикала.)

О чем приходится задумывать и помнить при решении иррационального уравнения? ( Надо помнить об области допустимых значений переменной в уравнении – об ОДЗ).

3) Для следующих уравнений назовите ОДЗ:

4) В следующих случаях восстановите запись:

5) Что нам показывают две последние записи? ( Два стандартных способа решения простейших иррациональных уравнений.)

6) Назовите эти способы (- замена уравнения уравнением-следствием путем возведения обеих частей уравнения в квадрат с обязательной последующей проверкой корней уравнения-следствия в исходном уравнении; — замена иррационального уравнения равносильной смешанной системой).

2. Систематизация и закрепление материала : (формы на данном этапе: фронтальная и индивидуальная работа; методы: наглядный, частично — поисковый, проблемный).

2.1. Фронтальная беседа с обучающимися:

Полностью алгоритмизировать процесс преобразования нельзя, однако полезно запомнить некоторые приемы, общие для всех типов уравнений.

1).Уравнение вида А(х)•В(х) = О, где А(х) и В(х) — многочлены относительно х, называют распадающимся уравнением .

Множество всех корней распадающегося уравнения есть объединение множеств всех корней двух уравнений А(х)=0 и В(х)=0. К уравнениям вида А(х)=0 применяется метод разложения на множители. Суть этого метода : нужно решить уравнение А(х)=0, где А(х)=А ₁ (х)А ₂ (х)А ₃ (х). Уравнение А(х)=0 заменяют совокупностью простых уравнений: А ₁ (х)=0,А ₂ (х)=0,А ₃ (х)=0. Находят корни уравнений этой совокупности и делают проверку. Метод разложения на множители используется в основном для рациональных и тригонометрических уравнений (примеры 1-2).

2).Уравнение вида , где А(х) и В(х) — многочлены относительно х (пример3)

где А(х), В(х), С(х) и D(х) — многочлены относительно х, обычно решают по следующему правилу.

Решают уравнение А(х)•D(х) — С(х)·В(х) = 0 и отбирают из его корней те, которые не обращают в нуль знаменатель уравнения (пример 4).

2.2. Решение рациональных уравнений и систем: № 33.1(а,б).

Уравнение распадается на два уравнения.

Значит, уравнение исходное имеет корни х ₁ = 2, х ₂ = 3, х ₃ = -2, х ₄ =1. Ответ. -2; 1; 2; 3.

ПРИМЕР 2 . Решим уравнение х 3 -7х+6=0.

Сначала решим уравнение

Подставив эти числа в знаменатель левой части исходного уравнения, получим

х ₂ 2 — х ₂ — 6 = 49 + 7 — 6 = 50 ≠0.

Это показывает, что число х ₁ = 3 не является корнем исходного уравнения, а число х ₂ =- 7 — корень этого уравнения. Ответ. -7.

х 2 — 5х + 6 — (2х + 3) (х — 3) = 0.

Число х ₁ не обращает в нуль знаменатель х — 3, а число х ₂ обращает. Следовательно, уравнение имеет единственный корень = -5. Ответ. -5.

Найти корни рационального уравнения часто помогает замена неизвестного. Умение удачно ввести новую переменную- важный элемент математической культуры. Удачный выбор новой переменной делает структуру уравнения более прозрачной.

Решим уравнение х 8 + 4х 6 -10х 4 + 4х 2 + 1 = 0.

Число х ₀ = 0 не является корнем уравнения, поэтому уравнение равносильно уравнению

х 4 + 4х 2 — 10 + + =0

Обозначим t = ,тогда х 4 += t 2 -2 ,

получаем t 2 + 4t — 12 = 0, х ₁ = 2 и х ₂ = -6.

Следовательно, корни уравнения найдем, объединив все корни двух уравнений: =2, и =-6,

Первое уравнение имеет два корня -1 и 1, а второе уравнение не имеет действительных корней, поэтому уравнение имеет только два корня: -1 и 1. Ответ. -1; 1.

2.3. Решение иррациональных уравнений и систем:№ 33.14(а, б).

💡 Видео

Дробно-рациональные уравнения. 8 класс.Скачать

Как решать уравнение с корнями Иррациональное уравнение Как решать уравнение с корнем х под корнемСкачать

Решение неравенства методом интерваловСкачать

ЛУЧШАЯ СТРАТЕГИЯ решения Целых Рациональных Уравнений (математика с нуля)Скачать

Как понять неравенства? Квадратные неравенства. Линейные и сложные неравенства | TutorOnlineСкачать

Иррациональные неравенства. 11 класс.Скачать

Равносильность уравнений и неравенств. Видеоурок 7. Алгебра 10 классСкачать

Иррациональные неравенства | Математика ЕГЭ 10 класс | УмскулСкачать

иррациональные неравенства методом интервалов 1Скачать