Решение прикладных задач с использованием дифференциальных уравнений

Видео:Задача Коши ➜ Частное решение линейного однородного дифференциального уравненияСкачать

Методические основы обучения студентов решению прикладных задач по теме «Дифференциальные уравнения» Текст научной статьи по специальности « Математика»

Видео:18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать

Аннотация научной статьи по математике, автор научной работы — Полюхович Надежда Васильевна

В статье раскрыты методические основы обучения студентов решению прикладных задач , способствующие преодоле­нию затруднений, возникающих при выяснении вида дифференциального уравнения первого порядка и при составлении дифференциального уравнения процесса, представленного в условии прикладной задачи .

Видео:Решение физических задач с помощью дифференциальных уравненийСкачать

Похожие темы научных работ по математике , автор научной работы — Полюхович Надежда Васильевна

Видео:Поле направлений дифференциального уравнения первого порядкаСкачать

The Methodical Fundamentals of a Student’s Training to Solve Applied Problems on the subject «Differential Equation»

The article exposes methodical fundamentals of a student’s training to solve applied problems, helping to overcome difficulties, which students have while determining the type of a differential equation of the first order and to make a differential equation of the process given in the data of the applied problem.

Видео:Откуда появляются дифференциальные уравнения и как их решатьСкачать

Текст научной работы на тему «Методические основы обучения студентов решению прикладных задач по теме «Дифференциальные уравнения»»

Методические основы обучения студентов решению прикладных задач по теме «Дифференциальные уравнения»

В статье раскрыты методические основы обучения студентов решению прикладных задач, способствующие преодолению затруднений, возникающих при выяснении вида дифференциального уравнения первого порядка и при составлении дифференциального уравнения процесса, представленного в условии прикладной задачи.

Ключевые слова: прикладная задача, методическая основа, дифференциальное уравнение, учебное затруднение.

The Methodical Fundamentals of a Student’s Training to Solve Applied Problems on the subject «Differential Equation»

N. V. Polukhovich

The article exposes methodical fundamentals of a student’s training to solve applied problems, helping to overcome difficulties, which students have while determining the type of a differential equation of the first order and to make a differential equation of the process given in the data of the applied problem.

Key words: an applied problem, methodical fundamental, the differential equation, educational difficulty.

В последнее время изменились требования, предъявляемые к знаниям и умениям специалистов: работник-исполнитель уступает место специалисту, к которому предъявляются повышенные требования. Он должен не только знать свою специальность, но и уметь самостоятельно мыслить, иметь навык исследовательской работы, уметь использовать полученные знания при решении конкретных задач. Все эти качества должны вырабатываться в вузе при изучении естественно-научных и математических дисциплин. Одним из средств формирования таких качеств на занятиях по математике является обучение студентов решению прикладных задач.

Теме исследования прикладных задач посвящено много диссертационных исследований. А. Б. Дмитриевой разработана методика обучения студентов самостоятельному решению прикладных задач и блок задач военно-прикладного содержания по теме «Теория вероятностей» [4]. Р. М. Зайкин, Н. В. Вахрушева и Т. В. Игнатьева предлагают использовать в процессе обучения цепочки взаимосвязанных задач с целью усиления прикладной направленности обучения математике. В работе Р. М. Зайкина [5] охарактеризованы способы составления математических профессионально ориентированных задач юридической тематики и цепочки таких задач. Н. В. Вахрушева [2] выделила две стратегии построения цепочек профессионально ориентированных задач и предложила комплексы цепочек профессионально ориентированных задач экономической тематики. Т. В. Игнатьевой [7] разработаны задачи-компакты прикладной направленности и способы их конструирования. Такие задачи автор

предлагает использовать в качестве средства совершенствования обучения математике в техническом вузе. Л. В. Васяк [1] предлагает использовать профессионально ориентированные задачи в качестве средства формирования профессиональной компетентности будущих инженеров. Н. В. Скоробогатовой [15] выявлены критерии отбора и дидактические функции профессионально ориентированных задач в обучении математике будущих инженеров, разработана и обоснована методика отбора и исследования таких задач в обучении математике студентов инженерных специальностей технических вузов с применением технологии наглядного моделирования.

Рассмотрим прикладные задачи в теме «Дифференциальные уравнения». При изучении этой темы студентам нужно усвоить основной материал (научиться определять вид дифференциального уравнения, способы решения уравнений, составлять дифференциальные уравнения при решении прикладных физических, геометрических и экономических задач) и научиться самостоятельно работать с прикладными задачами. Практика показывает, что у студентов возникают затруднения при изучении темы «Дифференциальные уравнения». Первое затруднение связано с определением вида дифференциального уравнения первого порядка. Одной из причин этого затруднения является то, что в учебниках все виды уравнений заданы символьно (общими формулами), словесного описания признаков каждого вида уравнения не приводится, а как известно из психологии, если признаки словесно не сформулированы, то это затрудняет формирование соответствующего умения. Еще одной причиной яв-

ляется отсутствие общей для всех видов дифференциальных уравнений первого порядка «инструкции», следуя которой студенты смогли бы определить вид дифференциального уравнения. Поэтому мы пришли к выводу, что нужно создать методические основы (ориентиры), пользуясь которыми студенты смогли бы определить вид дифференциального уравнения. Эти ориентиры должны иметь обобщенный характер и быть применимы при определении вида любого дифференциального уравнения первого порядка. Реализацией таких методических основ является разработанная нами схема выяснения вида дифференциального уравнения первого порядка (схема 1) [13]. Она основана на следующем: сначала нужно выразить производную, а затем в определенной последовательности действий проанализировать правую часть полученного равенства.

Поскольку существуют дифференциальные уравнения, которые относятся к более чем одному виду (например, уравнение У = — можно

считать уравнением с разделяющимися переменными, так как его правую часть можно представить в виде произведения двух функций, каждая из которых зависит только от одной переменной , 1

у = — ■ у , а также это уравнение можно считать х

однородным, так как его правая часть представляет собой функцию, зависящую только от у ),

схема 1 определит такие уравнения к видам с наиболее рациональными способами решения (уравнение, приведенное выше, схемой будет определено как уравнение с разделяющимися переменными).

Покажем, как работает схема 1 при определении вида дифференциального уравнения 3х2 + 6ху2 + (6х2у + 4у3 )■ — = 0 . Согласно схеме 1, сначала выразим производную

у =-2-V . Далее анализируем правую

часть полученного равенства. Представить ее в виде произведения двух функций, каждая из которых зависит только от одной переменной, не удается, поэтому далее пробуем представить ее в

виде функции, зависящей только от — , но и это

не удается. Представить правую часть в виде суммы К(х) ■ у + В(х) ■ у», где п Ф 1, тоже не удалось. Поэтому необходимо проверить выполнимость следующего условия (числитель)’у = —(знаменатель)’х . Вычислим указанные частные производные (числителъ)’у = (—3х2 — 6 ху2)— = —12 ху,

(знаменатель)’х = (6х2у + 4у3)’х = 12ху . Итак, видим, что проверяемое условие выполняется, поэтому делаем вывод, что рассматриваемое дифференциальное уравнение является уравнением в полных дифференциалах.

Созданная схема 1 проверялась двумя способами: через анализ всех видов дифференциальных уравнений первого порядка, представленных в учебниках [3; 8; 9], и через анализ самостоятельной деятельности студентов по определению вида дифференциального уравнения с использованием данной схемы.

Эксперимент показал, что результаты студентов, которых обучали определению вида дифференциального уравнения первого порядка с использованием предложенной схемы, значительно выше результатов студентов, которые обучались традиционно.

Следующее затруднение возникает у студентов при решении прикладных задач, сводящихся к дифференциальному уравнению, и связано с составлением дифференциального уравнения процесса, представленного в условии задачи.

Причина этого затруднения заключается в том, что в литературе не раскрывается список действий, которые нужно осуществить, чтобы составить дифференциальное уравнение процесса, представленного в условии прикладной задачи.

Мы выяснили, что процесс составления дифференциального уравнения зависит от типа задачи (физическая, геометрическая), каждый из которых имеет свои особенности. Поэтому для прикладных физических и геометрических задач нами сконструированы схемы их решения, где указаны действия, которые необходимо выполнить, чтобы составить дифференциальное уравнение процесса, представленного в условии задачи.

Рассмотрим схему решения прикладных физических задач [10]. Эта схема основана на модельном подходе и включает в себя следующие этапы: 1) составление дифференциального уравнения; 2) работа с дифференциальным уравнением; 3) интерпретация результатов.

Рассмотрим этап составления дифференциального уравнения. Для осуществления этого этапа нужно выполнить следующие промежуточные действия: 1) определить, существует ли физический закон, регулирующий процесс, представленный в условии задачи. Далее последовательность действий зависит от ответа на первый вопрос.

Если ответ положителен (такие задачи мы называем прикладными физическими задачами первого вида), то нужно выполнить следующую последовательность действий: 2) записать равенство, соответствующее физическому закону;

3) определить, какая из величин рассматриваемого процесса является независимой переменной;

4) выразить изменяющиеся величины через независимую переменную и данные задачи. Для этого: а) выразить одну изменяющуюся величину из составленного равенства через данные задачи; б) выразить остальные изменяющиеся величины из составленного равенства, используя физический смысл производной.

Если ответ на первый вопрос отрицателен (такие задачи мы называем прикладными физическими задачами второго вида), то последовательность действий будет следующей: 2) выбрать величины, одна из которых будет независимой переменной, а другая искомой функцией, и ввести для них обозначения; 3) выразить изменение искомой функции, которое будет соответствовать приращению независимой переменной. Для этого необходимо: а) найти «положительное» приращение искомой функции; б) найти «отрицательное» приращение искомой функции; в) записать «полное» приращение искомой функции.

Реализация второго и третьего этапа схемы решения прикладных физических задач обычно не вызывает затруднений.

Описанные выше этапы легко представить в виде граф-схемы [10].

Практика показала: чтобы студенты успешно самостоятельно решали прикладные физические задачи, нужно еще каждый этап схемы отработать на специально подобранных упражнениях. С этой целью нами созданы комплексы пошаговых упражнений [12] на отработку наиболее сложных этапов решения прикладных физических задач двух видов, а также дидактические материалы к ним [14]. В комплексы пошаговых упражнений включены только задания на отработку действий, необходимых для составления дифференциального уравнения. Дидактические материалы, которые мы предлагаем использовать в процессе обучения студентов решению прикладных задач, можно разделить на два вида: 1) дидактические материалы, используемые во время аудиторных занятий; 2) дидактические материалы для самостоятельной работы студентов дома. Оба вида дидактических материалов сконструированы согласно следующим требованиям: 1) дидактический материал должен быть обучающим (раскрывать состав математической деятельности, помогать преодолевать математические затруднения); 2) дидактический материал должен быть комплексным (учитывать не только математическое содержание, но и организацию работы с ним).

Далее рассмотрим схему решения прикладных геометрических задач, сводящихся к дифференциальному уравнению (схема 2) [11]. Работая над созданием этой схемы, мы обнаружили, что в тексте каждой прикладной геометрической задачи содержится условие, которое можно записать в виде равенства. Далее задачи делятся на два вида. В ряде задач для каждой составляющей этого равенства существует формула, позволяющая выразить искомые составляющие через переменные х, у, у’, у»,

Пример 1. Кривая проходит через точку А(0,а), МN — произвольная ордината этой кривой. Определить кривую из условия, что площадь 5’ОАМ/ =аЬ, где L — длина дуги АМ [8, с. 210]. В данной задаче заданным равенством является Б=аЬ; составляющие 5″ и L вычисляются по формулам

5 = | у ах, Ь = у 1 + (у’)

В других задачах соответствующих формул нет. Пример 2. Определить кривые, у которых радиус кривизны вдвое больше длины нормали [8, с.

217]. В этой задаче заданным условием будет: . Для радиуса кривизны существует

-у у ‘ , выражающая эту

составляющую через у, у’, у». Для составляющей ММ формулы, выражающей ее через х, у, у, у’, у». нет. Поэтому для выражения этой составляющей

Схема 2. Решение прикладных геометрических задач, сводящихся к дифференщстъному уравнению

через указанные переменные нужно ввести в рассмотрение координаты (х, у) произвольной точки М искомой кривой и угол а наклона касательной к кривой, проходящей через эту точку.

В дальнейшем планируем создать методику работы с прикладными экономическими задачами.

Выразить нужные величины через переменные х, у, у’ у». где у’^о а

Составить дифф еренциальное уравнение на основе заданного в условии равенства

1. Васяк, Л. В. Формирование профессиональной компетентности будущих инженеров в условиях интеграции математики и спецдисциплин средствами профессионально ориентированных задач [Текст] : авто-реф. дис. . канд. пед. наук / Л. В. Васяк. — Омск , 2007. — 20 с.

2. Вахрушева, Н. В. Использование цепочек взаимосвязанных задач в реализации профессиональной направленности обучения математике в экономическом вузе [Текст] : дис. . канд. пед. наук / Н. В. Вахрушева. — Орел , 2006. — 156 с.

3. Данко, П. Е. Высшая математика в упражнениях и задачах. Ч. II. Изд. 2-е. [Текст] : учеб. пособие для втузов / П. Е. Данко, А. Г. Попов. — М. : Высшая школа, 1974. — 464 с.

4. Дмитриева, А. Б. Самостоятельная работа по решению прикладных задач в курсе математики как условие повышения качества профессиональной подготовки обучаемых в вузе [Текст] : автореф. дис. . канд. пед. наук / А. Б. Дмитриева. — М. , 2004. — 18 с.

5. Зайкин, Р. М. Реализация профессиональной направленности математической подготовки на юридических факультетах [Текст] : автореф. дис. . канд.

пед. наук / Р. М. Зайкин. — Нижний Новгород, 2004. -18 с.

6. Зайниев, Р. М. Задачи и упражнения по математике с практическим содержанием [Текст] : учебное пособие для студентов, обучающихся по направлениям и специальностям техники и технологии / Р. М. Зайниев. — Набережные Челны : Изд-во Камской гос. инж.-экон. акад. , 2008. — 80 с.

7. Игнатьева, Т. В. Конструирование задач-компактов прикладной направленности и их использование в качестве средства совершенствования обучения математике в технических вузах [Текст] : автореф. дис. . канд. пед. наук / Т. В. Игнатьева. — Нижний Новгород, 2009. — 21 с.

8. Минорский, В. П. Сборник задач по высшей математике [Текст] : учеб. пособие для втузов / В. П. Минорский. — 14-е изд. , испр. — М. : Изд-во физико-математической литературы, 2004. — 336 с.

9. Пискунов, Н. С. Дифференциальное и интегральное исчисления для втузов, т. 2 [Текст] : учеб. пособие для втузов / Н. С. Пискунов. — 13-е изд. — М. : Наука, Главная редакция физико-математической литературы, 1985. — 560 с.

10. Полюхович, Н. В. Схема решения прикладных физических задач с использованием обыкновенных дифференциальных уравнений [Текст] / Н. В. Полюхо-вич // Математический вестник педвузов и университетов Волго-Вятского региона. Выпуск 10: Периодический межвузовский сборник научно-методических работ. — Киров : Изд-во ВятГГУ, 2008. — 356 с.

11. Полюхович, Н. В. Схема решения геометрических задач на составление дифференциальных уравнений [Текст] / Н. В. Полюхович // Задачи в обучении математике: теория, опыт, инновации : материалы Всероссийской научно-практической конференции, посвященной 115-летию чл. корр. АПН СССР П. А. Ларичева. — Вологда : Русь, 2007. — 414 с.

12. Полюхович, Н. В. Обучение решению прикладных физических задач по теме «Дифференциальные уравнения» [Текст] / Н. В. Полюхович // Образование в техническом вузе в XXI веке: Международный межвузовский научно-методический сборник / ГОУ ВПО «Камская государственная инженерно-экономическая академия». — Вып. 3. — Набережные Челны : Изд-во Кам. гос. инж. -экон. акад. , 2008. — 142 с.

13. Полюхович, Н. В. Схема выяснения вида дифференциального уравнения первого порядка [Текст] / Н. В. Полюхович // Преподавание математики в вузах и школах: проблемы содержания, технологии и методики: материалы Второй региональной научно-практической конференции. — Глазов : Изд-во Глазов. гос. пед. ин-та, 2006. — 128 с.

14. Полюхович, Н. В. Дидактический материал как основа обучения прикладным задачам по теме «Дифференциальные уравнения» [Текст] / Н. В. Полюхо-вич // Проблемы математического образования : материалы Международной научно-методической конференции. — Черкассы : Изд-во ЧНУ им. Б. Хмельницкого, 2009. — 290 с.

15. Скоробогатова, Н. В. Наглядное моделирование профессионально ориентированных задач в обучении математике студентов инженерных направлений технических вузов [Текст] : автореф. дис. . канд. пед. наук / Н. В. Скоробогатова. — М. , 2007. — 23 с.

Видео:Решение физических задач с помощью дифференциальных уравнений. Часть 2Скачать

Занятие по математике (2 курс) Решение задач прикладного характера на составление дифференциальных уравнений

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Решение задач прикладного характера на составление дифференциальных уравнений.

Преподаватель математики Елена Геннадьевна Шерстнева

ЗАНЯТИЕ ПО МАТЕМАТИКЕ ( 2 КУРС)

Решение задач прикладного характера на составление дифференциальных уравнений .

Вид занятия: Применение знаний, умений и навыков полученных при изучении дифференциальных уравнений.

Учебные: показать алгоритм решения задач на составление дифференциальных уравнений, познакомить с математическими моделями в физике, биологии, экономике. Учащиеся должны понимать сущность приложения математики к решению технических задач, которая заключается в том, что задачу переводят на язык математики, решают ее, как принято в математике, и интерпретируют на языке исходных данных.

Воспитательные. Формировать научное мировоззрение. Продолжить знакомить учащихся с понятием математического моделирования, рассказать о том, что одними и теми же дифференциальными уравнениями можно описывать совершенно разные реальные процессы, например электротехнические, механические и другие, т.е. дифференциальные уравнения как математические модели обладают большой общностью и в этом их важное философское и познавательное значение.

Межпредметные связи. Рассматриваемые на занятии математические модели в физике, биологии, экономике помогут увидеть силу межпредметных связей, важную роль математики, дающей мощный аппарат для решения многих задач, которые выдвигаются и успешно решаются в различных областях науки и практики.

Мотивация познавательной деятельности учащихся. Показать практическую значимость изучаемого материала, его широкое применение в общетехнических и специальных дисциплинах. Многие производственные процессы описываются дифференциальными уравнениями. Поэтому важно не только уметь решать сами дифференциальные уравнения, но и уметь составлять эти уравнения исходя из практической потребности.

Основные знания и умения: иметь понятие о решении несложных задач на составление дифференциальных уравнений по физике, электротехнике, экономике.

Раздаточный материал: Опорный конспект с планом занятия и набором задач для решения.

Технические средства обучения: использование фрагментов из компьютерной программы обучения «Функции и графики», компьютерная презентация конструкторской задачи.

Литература: 1. Валуцэ И.И. Математика для техникумов

2. Соловейчик И.Л. Сборник задач по математике для техникумов

3. Баврин И.И. Начала анализа и математические модели в естествознании и

4. Филимонова Е.В. Математика (среднее профессиональное образование).

Вопросы и упражнения для выполнения на занятии

Какое уравнение называется дифференциальным?

Назовите виды дифференциальных уравнений.

Решите уравнение: 2у dx = (1+ x ) dy . Найти уравнение интегральной кривой, проходящей через точку (1; 4). Задача Коши.

Скорость размножения некоторых бактерий пропорциональна их количеству М в рассматриваемый момент времени t . Найти зависимость количества бактерий от времени. Начальные условия М =М при t =0

Скорость распада радия пропорциональна его начальному количеству R в данный момент времени t . Найти закон радиоактивного распада. Начальные условия R = R ₀ при t =0.

Скорость изменения количества населения прямо пропорциональна этому количеству А на данный период времени. Построить математическую модель прироста (убыли) населения. Начальные условия А = А при t =0.

Решить уравнение: ху ‘ + у = х (х ≠ 0).

Инженерно-конструкторская задача. Найти форму автомобильной фары так, чтобы все лучи от зеркала фары шли цилиндрическим световым пучком.

Задача «Истощение ресурсов» В 1980 году для обеспечения пищей одного человека требовалась площадь 0,1 га и на земном шаре было 4000 млн га пахотной земли. Предположим, что с 1980 г эти условия по настоящее время не изменились и не изменятся в будущем, а также не появились и не появятся новые источники пищи. Тогда население Земли должно быть ограничено количеством 40 000 млн человек. Когда будет достигнут этот предел насыщения, если в 1980 году оно составляло 3600 млн человек и непрерывно растет со скоростью 1,7 % в год.

Дополнительные задачи: Скорость прямолинейного движения точки выражается формулой V = 3 + 4 t . Найдите уравнение движения точки, если S = 10 м при t =1 c

Подумайте, какая функция может являться решением уравнения: у » = — k 2 у (уравнение гармонических колебаний). Вторая производная функции равна самой функции с точностью до постоянного множителя.

Запишите домашнее задание №10, 107 учебник И.И. Валуцэ стр.351

«Скорость обесценивания оборудования вследствие его износа в данный момент времени пропорциональна его фактической стоимости ……»

Подведение итогов урока

Математическая модель, основанная на некотором упрощении, никогда не бывает тождественна рассматриваемому объекту, не передает всех его свойств и особенностей, а является его приближенным отражением. Однако, благодаря замене реального объекта соответствующей ему моделью появляется возможность математически сформулировать задачу его изучения и воспользоваться для анализа его свойств математическим аппаратом, который не зависит от конкретной природы данного объекта. Этот аппарат позволяет единообразно описать широкий круг фактов и наблюдений, провести их детальный количественный анализ, предсказать, как поведет себя объект в различных условиях, т.е. прогнозировать результаты будущих наблюдений.

В 1917 году Эйнштейн сделал первую попытку применить общую теорию относительности для описания пространственно временной структуры Вселенной. А основные уравнения теории относительности – это дифференциальные уравнения, имеющие множество решений. Отсюда множество моделей Вселенной.

Дифференциальные уравнения показательного роста (убывания).

Дифференциальные уравнения имеют большое прикладное значение, являясь мощным орудием исследования задач естествознания и техники, они широко используются в механике, астрономии, физике, во многих задачах химии, биологии. Это объясняется тем, что весьма часто объективные законы, которым подчиняются те или иные явления (процессы), записываются в форме дифференциальных уравнений, а сами эти уравнения являются средством для количественного выражения этих законов. Например, законы механики Ньютона позволяют механическую задачу описания движения системы материальных точек или твердого тела свести к математической задаче нахождения решений дифференциальных уравнений. Расчет радиотехнических схем и вычисление траектории спутников, исследование устойчивости самолета в полете и выяснение течения химических реакций – все это производится путем изучения и решения дифференциальных уравнений.

Мы будем рассматривать дифференциальное уравнение вида:

где k – const , причем k может быть : k > 0 или k

Зная формулу производной показательной функции, легко догадаться, что решением этого уравнения, является любая функция вида:

т.к. C – произвольная постоянная, то уравнение имеет бесконечно много решений.

Смысл дифференциального уравнения заключается в том, что скорость изменения функции в точке x пропорциональна значению самой функции в этой точке .

Приведем примеры, в которых величины изменяются по указанному закону .

Если r ‘ ( t ) скорость радиоактивного распада в момент времени t, то скорость уменьшения массы пропорциональна его количеству.

Значит, решением уравнения, является функция r ‘ ( t ) = С e — kt . Найдем из условия, что в начальный момент времени масса радиоактивного вещества была равна:

Промежуток времени T , через который масса радиоактивного вещества уменьшится в 2 раза называют “периодом полураспада”, зная Т , можно найти k :

Логарифмируя по основанию е , получаем — k T = – ln 2 ,

Например, для радия период полураспада . Поэтому, , следовательно, через 1 млн. лет от начальной массы r _o останется.

Задача: Скорость размножения бактерий m ‘ (t) связана с массой m(t) бактерий в момент времени t уравнением:

где k > 0, зависящее от вида бактерий и внешних условий.

Решениями этого уравнения являются функции m ( t ) = C · e kt .

Постоянную C можно найти из условия, что в момент t = 0 масса m _o бактерий известна, тогда

Задача. Два тела имеют одинаковую температуру – 100 0 . Они вынесены на воздух, его температура 0 0 . Через 10 мин. температура одного тела стала 80 0 , а второго – 64 0 . Через сколько минут после начала остывания разность их температур будет равна 25 0 .

Значит, 80 0 = 100 0 · e -10 k , e -10 k = 0,8

-10 k = ln 0,8,

2) 64 0 = 100 0 · 100 0 · e -10 k , тогда e -10 k = 0,64, следовательно -10 k = ln 0,64,

Следовательно

Ответ: t = 31,06 мин .

Задача. Задача о гармонических колебаниях.

В практике часто встречаются процессы, которые периодически повторяются например, колебательные движения маятника, струны, пружины, процессы связанные с переменным электрическим током, магнитным полем и т.д. Решение многих таких задач сводится к решению дифференциальных уравнений

где k – заданное положительное число

Инженерно-конструкторская задача. Найти форму автомобильной фары так, чтобы все лучи от зеркала фары шли цилиндрическим световым пучком. (Демонстрация презентации).

1.

2.

3.

4.

5.

Решаем квадратное уравнение относительно y’:

следовательно

Решим это уравнение, взяв + , заменяем на получаем

,умножаем обе части на dx , отсюда это однородное уравнение.

Сделаем замену y = z x и продифференцируем ее по x, получим dy = x dz + z dx , подставляем

Обе части делим на x получаем , раскрываем скобки и приводим подобные , разделяем переменные , интегрируем , решением будет функция далее , т.к , то раскрываем скобки в итоге получаем — это каноническое уравнение параболы с вершиной (; 0) и фокусом в точке (0;0).

Задача «Истощение ресурсов» В 1980 году для обеспечения пищей одного человека требовалась площадь 0,1 га и на земном шаре было 4000 млн га пахотной земли. Предположим, что с 1980 г эти условия по настоящее время не изменились и не изменятся в будущем, а так же не появились и не появятся новые источники пищи. Тогда население Земли должно быть ограничено количеством 40 000 млн человек. Когда будет достигнут этот предел насыщения, если в 1980 году оно составляло 3600 млн человек и непрерывно растет со скоростью 1,7 % в год.

Решение. А = А₀ e к t

А₀ = 3,6 · 10 9 , А = 40 · 10 9 , k = 0,017

40 · 10 9 = 3,6 · 10 9 · e 0,017t , t = (2 ln 10/3) /0,017 ≈ 142 г.

Ответ: В 2122 году наступит предел насыщения

Беседа о бережном отношении к природе и ее богатствам.

Видео:Дифференциальные уравнения: задача 2Скачать

Примеры решений задач по дифференциальным уравнениям

Теперь, когда вы научились находить производные и интегралы, самое время перейти к более сложной теме: решению дифференциальных уравнений (они же дифуры, диффуры и диф.уры :)), то есть уравнений, которые вместе с самой функцией (и/или аргументом), содержат и производную или даже несколько.

Как же решать дифференциальные уравнения? Главное, что понадобится, это а) умение правильно определить тип дифференциального уравнения и б) умение хорошо интегрировать — это существенная часть работы. А дальше следовать алгоримам для каждого из типов уравнений, которые подробно описаны в учебниках и ниже в примерах.

В этом разделе вы найдете решенные задачи на составление и решение дифференциальных уравнений. Примеры решений дифуров выложены бесплатно для вашего удобства и отсортированы по темам — изучайте, ищите похожие, решайте свои. Есть трудности в выполнении заданий? Мы готовы оказать помощь по дифференциальным уравнениям

Видео:Решение прикладных задач в области профессиональной деятельностиСкачать

Как решить дифференциальное уравнение онлайн?

Да ладно, неужели только вручную? Мучиться, определять тип, переносить, интегрировать, заменять, снова интегрировать, подставлять, выводить? Наверняка ведь есть онлайн-калькуляторы, которые позволяют решать дифференциальные уравнения?

У меня две новости, хорошая и плохая. Хорошая в том, что действительно самые распространенные типы дифференциальных уравнений математические программы умеют решать. Плохая в том, что обычно они выводят ответ (для научных расчетов этого достаточно), а не полное решение.

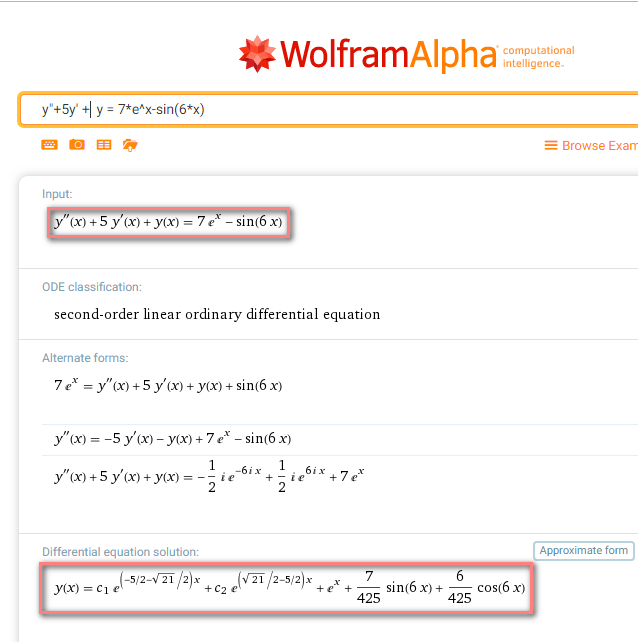
Есть известный математический сервис www.wolframalpha.com, которые представляет полные решения множества математических задач, в том числе диффуров онлайн (на английском языке) за 7 долларов в месяц. Ответы же доступны всем и могут помочь проверять правильность своего решения (см. ниже на скриншоте обведено само уравнение и его решение). Подробнее об этом сайте и типичных задачах, решаемых на нем, вы можете узнать тут.

Если вы забьете в поисковик что-то вроде «решить дифференциальное уравнение онлайн», то получите десятки ссылок на сайты, обещающие именно это.

Я проверила все сайты с первых страниц Яндекса и Гугла. Большая часть сайтов использует результаты расчетов www.wolframalpha.com (см. выше) и показывает вам ответ (и рекламу :)). Некоторые при этом не показывают даже ответа или говорят, что уравнение введено некорректно (хотя это вполне стандартное решаемое вручную линейное уравнение с постоянными коэффициентами). Полное решение не выдал ни один сайт.

Выводы? Бесплатно и полно и онлайн — не бывает. Хотите получать полные решения — используйте платную подписку на ВольфрамАльфа (или проконсультируйтесь у нас). Хотите ответы — там же бесплатно. Хотите научиться решать? Придется засучить рукава. Примеры на этой странице и ссылки внизу помогут вам. Удачи!

Видео:Дифференциальные уравнения. 11 класс.Скачать

Общий интеграл, семейство кривых

Задача 1. Показать, что функция $y^2-x^2-Cy=0$ является общим интегралом дифференциального уравнения $y'(x^2+y^2)-2xy=0.$

Задача 2. Составить дифференциальное уравнение семейства кривых $C_1 x+(y-C_2)^2=0.$

Видео:Решение дифференциальных уравнений. Практическая часть. 11 класс.Скачать

Решения дифференциальных уравнений 1 порядка

Задача 3. Найти общее решение линейного дифференциального уравнения первого порядка $ xy’+x^2+xy-y=0.$

Задача 4. Решить однородное дифференциальное уравнение $y’=-y/x quad (x ne 0).$

Задача 5. Решить дифференциальное уравнение $(y^4-2x^3y)dx+(x^4-2xy^3)dy=0.$

Задача 6. Решить однородное дифференциальное уравнение $(2x+y+1)dx+(x+2y-1)dy=0.$

Задача 7. Решить линейное дифференциальное уравнение первого порядка $y’-2xy=3x^2-2x^4.$

Задача 8. Решить дифференциальное уравнение $(x+y^2)y’=y-1.$

Видео:Решение физических задач при помощи диффуров | Дифференциальные уравненияСкачать

Решение задачи Коши для ДУ

Задача 9. Решить дифференциальное уравнение с разделяющимися переменными $(1+x^2)dy-2xydx=0.$ Найти частное решение, удовлетворяющее начальному условию $y(0)=1$.

Задача 10. Решить задачу Коши для дифференциального уравнения второго порядка $2y y» +1 =(y’)^2, , y(1/3)=1, , y'(1/3)=2$.

Задача 11. Найти решение задачи Коши для дифференциального уравнения $$ y’= frac, y(1)=1. $$

Задача 12. Решить задачу Коши для дифференциального уравнения третьего порядка $$ y»’=x+cos x, quad y(0)=0, y'(0)=0, y»(0)=0. $$

Видео:Лукьяненко Д. В. - Дифференциальные уравнения - Лекция 2Скачать

Решения дифференциальных уравнений 2 порядка

Задача 13. Решить дифференциальное уравнение второго порядка с постоянными коэффициентами $y»+4y’+4y=xe^.$

Задача 14. Решить задачу Коши для дифференциального уравнения второго порядка с постоянными коэффициентами методом вариации: $$ y»-3y’=frac<9e^><3+e^>, quad y(0)=4ln 4, y'(0)=3(3ln 4-1). $$

Видео:Задачи приводящие к дифференциальным уравнениям.Скачать

Cоставление дифференциальных уравнений

Задача 15. Скорость остывания нагретого тела пропорциональна разности температур тела и окружающей среды. За 10 минут тело охладилось от 100 до 60 градусов. Температура среды постоянна и равна 20 градусам. Когда тело остынет до 25 градусов?

Задача 16. Моторная лодка движется в спокойной воде со скоростью 5 м/сек. На полном ходу ее мотор выключается и через 40 сек после этого скорость лодки уменьшается до 2 м/сек. Определить скорость лодки через 2 минуты после остановки мотора, считая, что сопротивление воды пропорционально скорости движения лодки.

Видео:Решение задачи Коши дифференциального уравнения #maths #calculus #differentialequation #algebraСкачать

Решения нелинейных дифференциальных уравнений

Задача 17. Решить дифференциальное уравнение $y^2 ^2 -2xyy’+2y^2-x^2=0.$

Задача 18. Решить дифференциальное уравнение $^2-4xyy’+8y^2=0.$