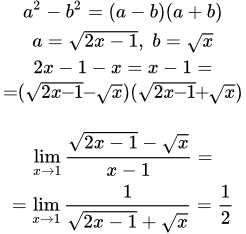Решение пределов с квадратными уравнениями примеры

Прежде чем рассказать о вычислении пределов с неопределенностью, хочется верить, что у вас уже есть понимание того, что такое предел и как вычислить элементарные пределы. Если такого понимания нет, то сначала прочитайте статью «Пределы. Понятие пределов. Вычисление пределов».
Теперь перейдем к рассмотрению пределов с неопределенностью.

Существует группа пределов, когда x , а функция представляет собой дробь, подставив в которую значение х = получим неопределенность вида .

Необходимо вычислить предел

Воспользуемся нашим правилом №1 и подставим в функцию. Как видно мы получаем неопределенность .

В числителе находим х в старшей степени, которая в нашем случае = 2:

То же самое проделаем со знаменателем:

Здесь также старшая степень = 2.

Далее надо из двух найденных степеней выбрать самую старшую. В нашем случае степень числителя и знаменателя совпадают и =2.

Итак, для раскрытия неопределенности нам потребуется разделить числитель и знаменатель на х в старшей степени, т.е. на x 2 :

Существуют также пределы с другой неопределенностью — вида . Отличие от предыдущего случая лишь в том, что х стремится уже не к , а к конечному числу.

Необходимо вычислить предел .

Снова воспользуемся правилом №1 и подставим в место х число -1:

Мы получили неопределенность , для раскрытия которой необходимо разложить числитель и знаменатель на множители, для чего в свою очередь обычно решается квадратное уравнение или используются формулы сокращенного умножения.

В нашем случае решаем уравнение:

.

Если корень не извлекается целый вероятней всего D вычислен неправильно.

Теперь находим корни уравнения:

В знаменателе у нас х + 1, что итак является простейшим множителем.

Тогда наш предел примет вид:

х + 1 красиво сокращается:

Теперь подставим вместо х значение -1 в функцию и получаем:

Рассмотрим основные положения, применяемые при решении различного рода задач с пределами:

Предел суммы 2-х или более функций равен сумме пределов этих функций:

Предел постоянной величины равен самой постоянной величине:

За знак предела можно выносить постоянный коэффициент:

Предел произведения 2-х и более функций равен произведению пределов этих функций ( последние должны существовать):

Предел отношения 2-х функций равен отношению пределов этих функций (в том случае, если предел знаменателя 0:

Степень функции, находящейся под знаком предела, применима к самому пределу этой функции (степень должна быть действительным числом):

На этом с вычислением пределов с неопределенностью всё. Еще в статье «Замечательные пределы: Первый и второй замечательный предел» мы отдельно рассматриваем интересную группу пределов. Статья вставит еще один блок для решения большинства пределов, встречающихся не просторах обучения.
Если у вас появились какие то вопросы по вычислению пределов с неопределенностью, то задавайте их в комментариях. Будем рады ответить.

Заметка: Если не хватает времени на учебу, вы можете заказать контрольную работу (http://forstuds.ru/kontrolnaya-rabota-na-zakaz), учтите правда наличие знаний по теме у вас после этого.

Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:

Вот с фразы «Воспользуемся нашим правилом №1» поподробнее пожалуйста. У вас есть отдельный список таких правил? Хочу себе сделать как бы карманный мини справочник, чтобы всегда был под рукой.

Я так и не понял как вы числитель разложили, будто колоду карт раскидали и все)

Видео:Вычислить предел. Пример 1.Скачать

Что такое предел функции

В данной публикации мы рассмотрим одно из главных понятий математического анализа – предел функции: его определение, а также различные способы решения с практическими примерами.

Видео:27. Вычисление предела функции №1. Примеры 1-4Скачать

Определение предела функции

Предел функции – величина, к которой стремится значение данной функции при стремлении ее аргумента к предельной для области определения точке.

Запись предела:

• предел обозначается значком lim;
• под ним добавляется, к какому значению стремится аргумент (переменная) функции. Обычно, это x , но не обязательно, например: “ x →1″;

Таким образом, финальная запись предела выглядит выглядит так (в нашем случае):

Читается как “предел функции при икс, стремящемся к единице”.

x →1 – это значит, что “икс” последовательно принимает значения, которые бесконечно приближаются к единице, но никогда с ней не совпадут (ее не достигнут).

Видео:Матан. Пределы для успешной сдачи зачёта | TutorOnline МатематикаСкачать

Решение пределов

С заданным числом

Давайте решим рассмотренный выше предел. Для этого просто подставляем единицу в функцию (т.к. x →1):

Таким образом, чтобы решить предел, сперва пробуем просто подставить заданное число в функцию под ним (если икс стремится к конкретному числу).

С бесконечностью

В данному случае аргумент функции бесконечно возрастает, то есть “икс” стремится к бесконечности (∞). Например:

Если x →∞, то заданная функция стремится к минус бесконечности (-∞), т.к.:

• 3 – 1 = 2
• 3 – 10 = -7
• 3 – 100 = -97
• 3 – 1000 – 997 и т.д.

Другой более сложный пример

Для того, чтобы решить этот предел, также, просто увеличиваем значения x и смотрим на “поведение” функции при этом.

Таким образом при “икс”, стремящемся к бесконечности, функция неограниченно растет.

С неопределенностью (икс стремится к бесконечности)

В данном случае речь идет про пределы, когда функция – это дробь, числитель и знаменатель которой представляют собой многочлены. При этом “икс” стремится к бесконечности.

Пример: давайте вычислим предел ниже.

Выражения и в числителе, и а знаменателе стремятся к бесконечности. Можно предположить, что в таком случае решение будет таким:

Однако не все так просто. Чтобы решить предел нам нужно сделать следующее:

1. Находим x в старшей степени для числителя (в нашем случае – это два).

2. Аналогичным образом определяем x в старшей степени для знаменателя (тоже равняется двум).

3. Теперь делим и числитель, и знаменатель на x в старшей степени. В нашем случае в обоих случаях – во второй, но если бы они были разные, следовало бы взять наибольшую степень.

4. В получившемся результате все дроби стремятся к нулю, следовательно ответ равен 1/2.

С неопределенностью (икс стремится к конкретному числу)

И в числителе, и в знаменателе представлены многочлены, однако, “икс” стремится к конкретному числу, а не к бесконечности.

В данном случае условно закрываем глаза на то, что в знаменателе стоит ноль.

Пример: Найдем предел функции ниже.

1. Для начала подставим в функцию число 1, к которому стремится “икс”. Получаем неопределенность рассматриваемого нами вида.

2. Далее раскладываем числитель и знаменатель на множители. Для этого можно воспользоваться формулами сокращенного умножения, если они подходят, или решить квадратное уравнение.

В нашем случаем корнями выражения в числителе () являются числа 1 и 1,5. Следовательно его можно представить в виде: .

Знаменатель () изначально является простым.

3. Получаем вот такой видоизмененный предел:

4. Дробь можно сократить на ():

5. Остается только подставить число 1 в выражение, получившееся под пределом:

Видео:36. Вычисление пределов функций с использованием 2-го замечательного пределаСкачать

Решение пределов с корнями

Видео:5 способов решения квадратного уравнения ➜ Как решать квадратные уравнения?Скачать

Методы решений

Для вычисления пределов с корнями, применяются приемы и методы, аналогичные методам вычисления пределов с многочленами (см. «Раскрытие неопределенностей с дробями», «Решение пределов с дробями из многочленов»). При этом возможны следующие дополнительные приемы, специфичные для функций с корнями.
1) Убрать корни с помощью подстановки, применяя теорему о пределе сложной функции. Примеры ⇓
2) Разделить числитель и знаменатель на x s (в случае неопределенности вида ∞/∞ при x → ∞ ), где s – некоторое подобранное число. Пример ⇓
3) Выразить бесконечно малые функции, содержащие корни, через бесконечно малые линейные функции, используя приведенные ниже формулы (то же самое в случае разности бесконечно больших функций). Примеры ⇓
4) Иногда удобно бесконечно малую функцию преобразовать в сумму или разность бесконечно малых функций, пределы от которых легко находятся. Пример ⇓

В последних двух случаях применяются следующие формулы:
;
;
;
. . . . . . . .
.
Например:
;
;
.

Эти же формулы применяют и для раскрытия разности бесконечно больших функций: .

Видео:Решение квадратных уравнений. Дискриминант. 8 класс.Скачать

Примеры решений

Все примеры Далее мы приводим подробные решения следующих примеров.
Найти предел последовательности:
решение ⇓
Найти следующие пределы функций с корнями:
⇓ , ⇓ , ⇓ , ⇓ , ⇓ .

Решение подстановкой

Пример 1

Подставим . Тогда .
При .
Мы имеем неопределенность вида .

Замечаем, что от корня можно освободится, если сделать подстановку .
Тогда функцию за знаком предела можно представить как сложную:
,
где , .
Тогда нам нужно найти предел сложной функции
, где .

Применим теорему о пределе сложной функции. Но поскольку функция строго монотонна, то мы применим ее разновидность – теорему о пределе функции от монотонной функции.

Для этого сначала вычисляем предел . Поскольку функция непрерывна на всей области определения, то этот предел равен значению функции в точке :
.

Теперь вычисляем второй предел:
.
Он не содержит корней. То есть мы свели задачу к пределу от разности дробей многочленов. Применяем методы, изложенные на странице «Решение пределов с дробями из многочленов».

Разложим знаменатель на множители и приводим дроби к общему знаменателю:
;

.
Делим числитель и знаменатель на . При имеем:
.
Находим предел:
.

По теореме о пределе функции от монотонной функции,
.

Пример 2

Все примеры ⇑ Найти предел последовательности:
.

Преобразуем элемент заданной последовательности, воспользовавшись свойствами корней:
.

Если мы найдем предел функции
,
то согласно определению предела функции по Гейне, искомый предел заданной последовательности будет равняться этому пределу: , поскольку при .

Находим предел отношения многочленов, выделяя и сокращая в числителе и знаменателе множитель :

.

Неопределенность ∞ / ∞

Пример 3

Все примеры ⇑ Найти предел отношения корней:
.

Здесь, при числитель и знаменатель стремятся к . У нас неопределенность вида . Для ее раскрытия, последовательно выносим бесконечно большую часть в числителе и знаменателе за скобки. При имеем:
;

;
;

;
.

Линеаризация бесконечно малых (больших) функций

Пример 4

Все примеры ⇑ Найти предел дроби с корнями:
.

Подставим в числитель и знаменатель:
;
.
Числитель и знаменатель обращаются в нуль. Мы имеем неопределенность вида 0/0 .
Для ее раскрытия, линеаризуем бесконечно малые функции, используя формулу:
(П4.1) .

Делим числитель и знаменатель на и находим предел:

.
Здесь , .

Пример 5

Подставим в числитель и знаменатель:
;
.
Мы имеем неопределенность вида 0/0 .

Чтобы упростить вычисления, здесь удобно представить бесконечно малые функции в числителе и знаменателе в виде сумм и разностей других бесконечно малых функций:
(П5.1) .

Применим формулу:
.
Подставим :
.
Отсюда
, где .
Заметим, что .

Применим формулу:
.
Подставим :
.
Отсюда
, где .
Заметим, что .

Применим формулу:
.
Подставим :

.
Отсюда
, где .
.

Наконец, применим формулу:
.
Подставим :

.
Отсюда
, где .
.

Подставляем полученные выражения в (П5.1):
.
Делим числитель и знаменатель на x . В результате мы освобождаемся от неопределенности и находим предел непрерывной функции:

.

Можно было записать и так:

.
После чего вычислить пределы:
.

Пример 6

Все примеры ⇑ Найти предел функции с корнями при x стремящемся к бесконечности:
.

Поскольку, при , и , то мы имеем неопределенность вида +∞ – (+∞) .

Применим формулу:
(П6.1) .
Подставим :

.
Отсюда, при имеем:
(П6.2) .

В числителе опять неопределенность +∞ – (+∞) . Применяем формулу (П6.1) еще раз. Подставим :

.
Отсюда
.

Подставим в (П6.2):
,
где .
Теперь у нас неопределенность вида ∞/∞ . Для раскрытия этой неопределенности, преобразуем знаменатель. Выделим бесконечно большую часть и вынесем ее за скобки. При имеем:
;

;
;

;
;
.

Делим числитель и знаменатель в функции на . При имеем:
.
Находим предел.
При , ,

.

Использованная литература:
Н.М. Гюнтер, Р.О. Кузьмин. Сборник задач по высшей математики. Том 1. Москва, 1957.
Л.Д. Кудрявцев, А.Д. Кутасов, В.И. Чехлов, М.И. Шабунин. Сборник задач по математическому анализу. Том 1. Москва, 2003.
Б.П. Демидович. Сборник задач и упражнений по математическому анализу. Москва, 1997.

Автор: Олег Одинцов . Опубликовано: 02-02-2019 Изменено: 30-11-2021

💥 Видео

29. Вычисление пределов функции №4. Неопределенность 0/0 с корнями.Скачать

Предел функции на бесконечности. 10 класс.Скачать

46. Вычисление пределов с помощью эквивалентных бесконечно малых функцийСкачать

28. Вычисление пределов функций №2. Неопределенность 0/0, заданная отношением двух многочленов.Скачать

Математика это не ИсламСкачать

33. Правило Лопиталя примеры с решениемСкачать

Матан за час. Шпаргалка для первокурсника. Высшая математикаСкачать

11. Вычисление предела последовательности ( предел отношения двух многочленов ), примеры 1 и 2.Скачать

13. Вычисление предела последовательности ( предел с корнями и степенями ), примеры 5 и 6.Скачать

Математика без Ху!ни. Пределы, часть1. Неопределенность, раскрытие неопределенностей.Скачать

Квадратные уравнения от «А» до «Я». Классификация, решение и теорема Виета | МатематикаСкачать

Пределы функций для чайников. Свойства пределов. Примеры решенияСкачать

Вычисление пределов #10Скачать

Как решать любое квадратное уравнение Полное Неполное квадр ур x^2+2x-3=0 5x^2-2x=0 2x^2-2=0 3x^2=0Скачать