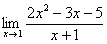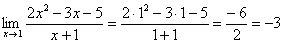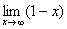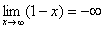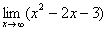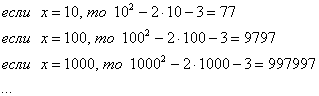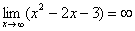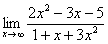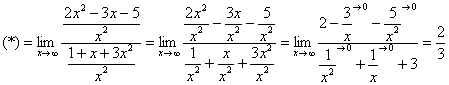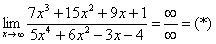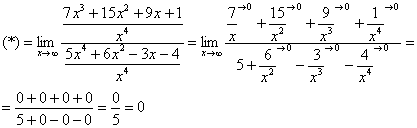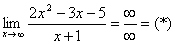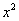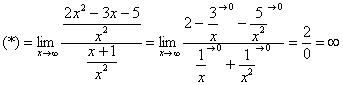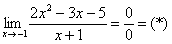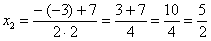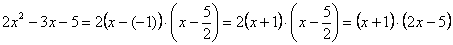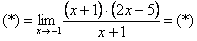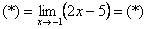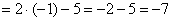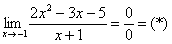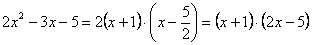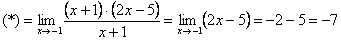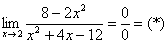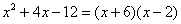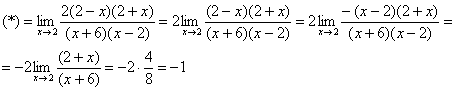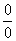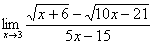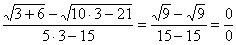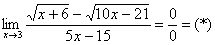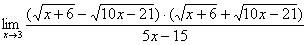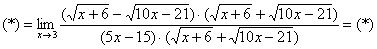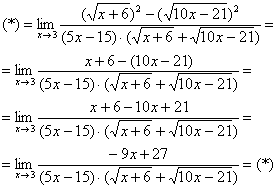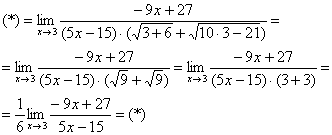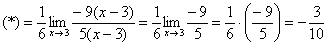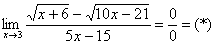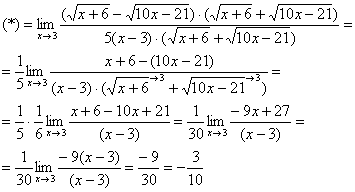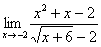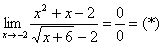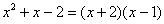Про уравнения - легко » Статьи

Решение пределов с квадратными уравнениями

Обновлено
Вычисление пределов. Пределы с неопределенностью

Прежде чем рассказать о вычислении пределов с неопределенностью, хочется верить, что у вас уже есть понимание того, что такое предел и как вычислить элементарные пределы. Если такого понимания нет, то сначала прочитайте статью «Пределы. Понятие пределов. Вычисление пределов».
Теперь перейдем к рассмотрению пределов с неопределенностью.

Существует группа пределов, когда x Решение пределов с квадратными уравнениямиРешение пределов с квадратными уравнениями, а функция представляет собой дробь, подставив в которую значение х = Решение пределов с квадратными уравнениямиполучим неопределенность вида Решение пределов с квадратными уравнениями.

Необходимо вычислить предел Решение пределов с квадратными уравнениями

Воспользуемся нашим правилом №1 и подставим Решение пределов с квадратными уравнениямив функцию. Как видно мы получаем неопределенность Решение пределов с квадратными уравнениями.

В числителе находим х в старшей степени, которая в нашем случае = 2:

Решение пределов с квадратными уравнениями

То же самое проделаем со знаменателем:

Решение пределов с квадратными уравнениями

Здесь также старшая степень = 2.

Далее надо из двух найденных степеней выбрать самую старшую. В нашем случае степень числителя и знаменателя совпадают и =2.

Итак, для раскрытия неопределенности Решение пределов с квадратными уравненияминам потребуется разделить числитель и знаменатель на х в старшей степени, т.е. на x 2 :

Решение пределов с квадратными уравнениями

Существуют также пределы с другой неопределенностью — вида Решение пределов с квадратными уравнениями. Отличие от предыдущего случая лишь в том, что х стремится уже не к Решение пределов с квадратными уравнениями, а к конечному числу.

Необходимо вычислить предел Решение пределов с квадратными уравнениями.

Снова воспользуемся правилом №1 и подставим в место х число -1:

Решение пределов с квадратными уравнениями

Мы получили неопределенность Решение пределов с квадратными уравнениями, для раскрытия которой необходимо разложить числитель и знаменатель на множители, для чего в свою очередь обычно решается квадратное уравнение или используются формулы сокращенного умножения.

В нашем случае решаем уравнение:

Решение пределов с квадратными уравнениями

Решение пределов с квадратными уравнениями

Решение пределов с квадратными уравнениями.

Если корень не извлекается целый вероятней всего D вычислен неправильно.

Теперь находим корни уравнения:

Решение пределов с квадратными уравнениями

Решение пределов с квадратными уравнениями

Решение пределов с квадратными уравнениями

В знаменателе у нас х + 1, что итак является простейшим множителем.

Тогда наш предел примет вид:

Решение пределов с квадратными уравнениями

х + 1 красиво сокращается:

Решение пределов с квадратными уравнениями

Теперь подставим вместо х значение -1 в функцию и получаем:

Рассмотрим основные положения, применяемые при решении различного рода задач с пределами:

    Предел суммы 2-х или более функций равен сумме пределов этих функций:

Решение пределов с квадратными уравнениями
Предел постоянной величины равен самой постоянной величине:

Решение пределов с квадратными уравнениями

За знак предела можно выносить постоянный коэффициент:

Решение пределов с квадратными уравнениями

Предел произведения 2-х и более функций равен произведению пределов этих функций ( последние должны существовать):

Решение пределов с квадратными уравнениями

Предел отношения 2-х функций равен отношению пределов этих функций (в том случае, если предел знаменателя Решение пределов с квадратными уравнениями0:

Решение пределов с квадратными уравнениями

Степень функции, находящейся под знаком предела, применима к самому пределу этой функции (степень должна быть действительным числом):

Решение пределов с квадратными уравнениями

На этом с вычислением пределов с неопределенностью всё. Еще в статье «Замечательные пределы: Первый и второй замечательный предел» мы отдельно рассматриваем интересную группу пределов. Статья вставит еще один блок для решения большинства пределов, встречающихся не просторах обучения.
Если у вас появились какие то вопросы по вычислению пределов с неопределенностью, то задавайте их в комментариях. Будем рады ответить.

Заметка: Если не хватает времени на учебу, вы можете заказать контрольную работу (http://forstuds.ru/kontrolnaya-rabota-na-zakaz), учтите правда наличие знаний по теме у вас после этого.

Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:

Вот с фразы «Воспользуемся нашим правилом №1» поподробнее пожалуйста. У вас есть отдельный список таких правил? Хочу себе сделать как бы карманный мини справочник, чтобы всегда был под рукой.

Я так и не понял как вы числитель разложили, будто колоду карт раскидали и все)

Содержание
  1. Решение пределов с квадратными уравнениями
  2. Предел по-шагам
  3. Результат
  4. Примеры пределов
  5. Правила ввода
  6. 🌟 Видео

Видео:Матан. Пределы для успешной сдачи зачёта | TutorOnline МатематикаСкачать

Матан. Пределы для успешной сдачи зачёта | TutorOnline Математика

Решение пределов с квадратными уравнениями

Теория пределов – это один из разделов математического анализа. Вопрос решения пределов является достаточно обширным, поскольку существуют десятки приемов решений пределов различных видов. Существуют десятки нюансов и хитростей, позволяющих решить тот или иной предел. Тем не менее, мы все-таки попробуем разобраться в основных типах пределов, которые наиболее часто встречаются на практике.

Начнем с самого понятия предела. Но сначала краткая историческая справка. Жил-был в 19 веке француз Огюстен Луи Коши, который заложил основы математического анализа и дал строгие определения, определение предела, в частности. Надо сказать, этот самый Коши снился, снится и будет сниться в кошмарных снах всем студентам физико-математических факультетов, так как доказал огромное количество теорем математического анализа, причем одна теорема отвратительнее другой. В этой связи мы не будем рассматривать строгое определение предела, а попытаемся сделать две вещи:

1. Понять, что такое предел.
2. Научиться решать основные типы пределов.

Прошу прощения за некоторую ненаучность объяснений, важно чтобы материал был понятен даже чайнику, что, собственно, и является задачей проекта.

Итак, что же такое предел?

А сразу пример, чего бабушку лохматить….

Решение пределов с квадратными уравнениями

Любой предел состоит из трех частей:

1) Всем известного значка предела 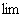Решение пределов с квадратными уравнениями.
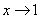
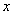
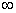
2) Записи под значком предела, в данном случае Решение пределов с квадратными уравнениями. Запись читается «икс стремится к единице». Чаще всего – именно Решение пределов с квадратными уравнениями, хотя вместо «икса» на практике встречаются и другие переменные. В практических заданиях на месте единицы может находиться совершенно любое число, а также бесконечность (Решение пределов с квадратными уравнениями).
3) Функции под знаком предела, в данном случае 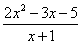Решение пределов с квадратными уравнениями.

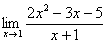
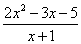
Сама запись Решение пределов с квадратными уравнениямичитается так: «предел функции Решение пределов с квадратными уравнениямипри икс стремящемся к единице».

Разберем следующий важный вопрос – а что значит выражение «икс стремится к единице»? И что вообще такое «стремится»?
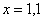
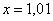
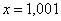
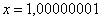
Понятие предела – это понятие, если так можно сказать, динамическое. Построим последовательность: сначала Решение пределов с квадратными уравнениями, затем Решение пределов с квадратными уравнениями, Решение пределов с квадратными уравнениями, …, Решение пределов с квадратными уравнениями, ….
То есть выражение «икс стремится к единице» следует понимать так – «икс» последовательно принимает значения, которые бесконечно близко приближаются к единице и практически с ней совпадают.

Как решить вышерассмотренный пример? Исходя из вышесказанного, нужно просто подставить единицу в функцию, стоящую под знаком предела:

Решение пределов с квадратными уравнениями

Итак, первое правило: Когда дан любой предел, сначала просто пытаемся подставить число в функцию.

Мы рассмотрели простейший предел, но и такие встречаются на практике, причем, не так уж редко!

Пример с бесконечностью:

Решение пределов с квадратными уравнениями

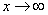
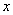
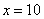
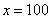
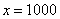
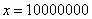
Разбираемся, что такое Решение пределов с квадратными уравнениями? Это тот случай, когда Решение пределов с квадратными уравненияминеограниченно возрастает, то есть: сначала Решение пределов с квадратными уравнениями, потом Решение пределов с квадратными уравнениями, потом Решение пределов с квадратными уравнениями, затем Решение пределов с квадратными уравнениямии так далее до бесконечности.

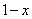
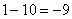
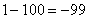
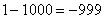
А что в это время происходит с функцией Решение пределов с квадратными уравнениями?
Решение пределов с квадратными уравнениями, Решение пределов с квадратными уравнениями, Решение пределов с квадратными уравнениями, …

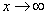
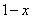
Итак: если Решение пределов с квадратными уравнениями, то функция Решение пределов с квадратными уравнениямистремится к минус бесконечности:

Решение пределов с квадратными уравнениями

Грубо говоря, согласно нашему первому правилу, мы вместо «икса» подставляем в функцию 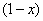Решение пределов с квадратными уравнениямибесконечность и получаем ответ.

Еще один пример с бесконечностью:

Решение пределов с квадратными уравнениями

Опять начинаем увеличивать 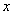Решение пределов с квадратными уравнениямидо бесконечности, и смотрим на поведение функции:
Решение пределов с квадратными уравнениями

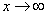
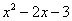
Вывод: при Решение пределов с квадратными уравнениямифункция Решение пределов с квадратными уравненияминеограниченно возрастает:
Решение пределов с квадратными уравнениями

И еще серия примеров:

Пожалуйста, попытайтесь самостоятельно мысленно проанализировать нижеследующее и запомните простейшие виды пределов:

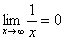
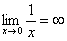
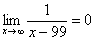
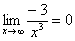
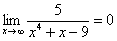
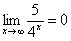
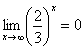
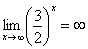
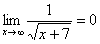
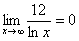
Решение пределов с квадратными уравнениями, Решение пределов с квадратными уравнениями, Решение пределов с квадратными уравнениями, Решение пределов с квадратными уравнениями, Решение пределов с квадратными уравнениями, Решение пределов с квадратными уравнениями, Решение пределов с квадратными уравнениями, Решение пределов с квадратными уравнениями, Решение пределов с квадратными уравнениями, Решение пределов с квадратными уравнениями
Если где-нибудь есть сомнения, то можете взять в руки калькулятор и немного потренироваться.
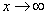
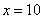
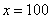
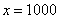
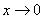
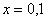
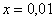
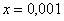
В том случае, если Решение пределов с квадратными уравнениями, попробуйте построить последовательность Решение пределов с квадратными уравнениями, Решение пределов с квадратными уравнениями, Решение пределов с квадратными уравнениями. Если Решение пределов с квадратными уравнениями, то Решение пределов с квадратными уравнениями, Решение пределов с квадратными уравнениями, Решение пределов с квадратными уравнениями.

Примечание: строго говоря, такой подход с построением последовательностей из нескольких чисел некорректен, но для понимания простейших примеров вполне подойдет.

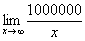
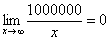
Также обратите внимание на следующую вещь. Даже если дан предел с большим числом вверху, да хоть с миллионом: Решение пределов с квадратными уравнениями, то все равно Решение пределов с квадратными уравнениями, так как рано или поздно «икс» примет такие гигантские значения, что миллион по сравнению с ними будет самым настоящим микробом.

Что нужно запомнить и понять из вышесказанного?

1) Когда дан любой предел, сначала просто пытаемся подставить число в функцию.

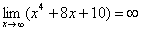
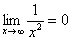
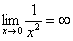
2) Вы должны понимать и сразу решать простейшие пределы, такие как Решение пределов с квадратными уравнениями, Решение пределов с квадратными уравнениями, Решение пределов с квадратными уравнениямии т.д.

Пределы с неопределенностью вида 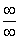Решение пределов с квадратными уравнениямии метод их решения

Сейчас мы рассмотрим группу пределов, когда 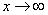Решение пределов с квадратными уравнениями, а функция представляет собой дробь, в числителе и знаменателе которой находятся многочлены

Вычислить предел Решение пределов с квадратными уравнениями

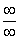
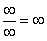
Согласно нашему правилу попытаемся подставить бесконечность в функцию. Что у нас получается вверху? Бесконечность. А что получается внизу? Тоже бесконечность. Таким образом, у нас есть так называемая неопределенность вида Решение пределов с квадратными уравнениями. Можно было бы подумать, что Решение пределов с квадратными уравнениями, и ответ готов, но в общем случае это вовсе не так, и нужно применить некоторый прием решения, который мы сейчас и рассмотрим.

Как решать пределы данного типа?

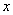
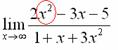
Сначала мы смотрим на числитель и находим Решение пределов с квадратными уравнениямив старшей степени:
Решение пределов с квадратными уравнениями
Старшая степень в числителе равна двум.

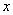
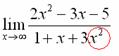
Теперь смотрим на знаменатель и тоже находим Решение пределов с квадратными уравнениямив старшей степени:
Решение пределов с квадратными уравнениями
Старшая степень знаменателя равна двум.

Затем мы выбираем самую старшую степень числителя и знаменателя: в данном примере они совпадают и равны двойке.

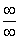
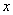
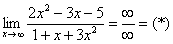
Итак, метод решения следующий: для того, чтобы раскрыть неопределенность Решение пределов с квадратными уравненияминеобходимо разделить числитель и знаменатель на Решение пределов с квадратными уравнениямив старшей степени.

Решение пределов с квадратными уравнениями
Разделим числитель и знаменатель на 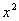Решение пределов с квадратными уравнениями
Решение пределов с квадратными уравнениями

Вот оно как, ответ 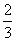Решение пределов с квадратными уравнениями, а вовсе не бесконечность.

Что принципиально важно в оформлении решения?

Во-первых, указываем неопределенность, если она есть.

Во-вторых, желательно прервать решение для промежуточных объяснений. Я обычно использую знак 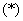Решение пределов с квадратными уравнениями, он не несет никакого математического смысла, а обозначает, что решение прервано для промежуточного объяснения.

В-третьих, в пределе желательно помечать, что и куда стремится. Когда работа оформляется от руки, удобнее это сделать так: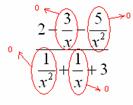
Решение пределов с квадратными уравнениями
Для пометок лучше использовать простой карандаш.

Конечно, можно ничего этого не делать, но тогда, возможно, преподаватель отметит недочеты в решении либо начнет задавать дополнительные вопросы по заданию. А оно Вам надо?

Найти предел 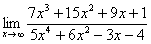Решение пределов с квадратными уравнениями
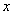
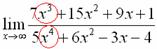
Снова в числителе и знаменателе находим Решение пределов с квадратными уравнениямив старшей степени:
Решение пределов с квадратными уравнениями
Максимальная степень в числителе: 3
Максимальная степень в знаменателе: 4
Выбираем наибольшее значение, в данном случае четверку.
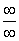
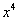
Согласно нашему алгоритму, для раскрытия неопределенности Решение пределов с квадратными уравнениямиделим числитель и знаменатель на Решение пределов с квадратными уравнениями.
Полное оформление задания может выглядеть так:

Решение пределов с квадратными уравнениями

Разделим числитель и знаменатель на Решение пределов с квадратными уравнениями

Решение пределов с квадратными уравнениями

Найти предел 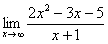Решение пределов с квадратными уравнениями
Максимальная степень «икса» в числителе: 2
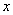
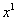
Максимальная степень «икса» в знаменателе: 1 ( Решение пределов с квадратными уравнениямиможно записать как Решение пределов с квадратными уравнениями)
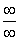
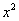
Для раскрытия неопределенности Решение пределов с квадратными уравненияминеобходимо разделить числитель и знаменатель на Решение пределов с квадратными уравнениями. Чистовой вариант решения может выглядеть так:

Решение пределов с квадратными уравнениями

Разделим числитель и знаменатель на Решение пределов с квадратными уравнениями

Решение пределов с квадратными уравнениями

Под записью 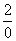Решение пределов с квадратными уравнениямиподразумевается не деление на ноль (делить на ноль нельзя), а деление на бесконечно малое число.

Таким образом, при раскрытии неопределенности вида 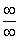Решение пределов с квадратными уравнениямиу нас может получиться конечное число, ноль или бесконечность.

Пределы с неопределенностью вида 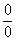Решение пределов с квадратными уравнениямии метод их решения

Предвосхищаю вопрос от чайников: «Почему здесь деление на ноль? На ноль же делить нельзя!». Смысл записи 0:0 будет понятен позже, после ознакомления с четвёртым уроком о бесконечно малых функциях. А пока всем начинающим изучать математический анализ предлагаю читать далее.

Следующая группа пределов чем-то похожа на только что рассмотренные пределы: в числителе и знаменателе находятся многочлены, но «икс» стремится уже не к бесконечности, а к конечному числу.

Решить предел Решение пределов с квадратными уравнениями
Сначала попробуем подставить -1 в дробь:
Решение пределов с квадратными уравнениями
В данном случае получена так называемая неопределенность Решение пределов с квадратными уравнениями.

Общее правило: если в числителе и знаменателе находятся многочлены, и имеется неопределенности вида 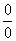Решение пределов с квадратными уравнениями, то для ее раскрытия нужно разложить числитель и знаменатель на множители.

Для этого чаще всего нужно решить квадратное уравнение и (или) использовать формулы сокращенного умножения. Если данные вещи позабылись, тогда посетите страницу Математические формулы и таблицы и ознакомьтесь с методическим материалом Горячие формулы школьного курса математики. Кстати его лучше всего распечатать, требуется очень часто, да и информация с бумаги усваивается лучше.

Итак, решаем наш предел
Решение пределов с квадратными уравнениями

Разложим числитель и знаменатель на множители

Для того чтобы разложить числитель на множители, нужно решить квадратное уравнение: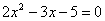
Решение пределов с квадратными уравнениями
Сначала находим дискриминант: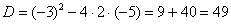
Решение пределов с квадратными уравнениями
И квадратный корень из него: 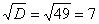Решение пределов с квадратными уравнениями.

В случае если дискриминант большой, например 361, используем калькулятор, функция извлечения квадратного корня есть на самом простом калькуляторе.

! Если корень не извлекается нацело (получается дробное число с запятой), очень вероятно, что дискриминант вычислен неверно либо в задании опечатка.

Далее находим корни: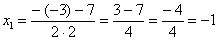
Решение пределов с квадратными уравнениями
Решение пределов с квадратными уравнениями

Таким образом:
Решение пределов с квадратными уравнениями

Всё. Числитель на множители разложен.

Знаменатель. Знаменатель 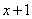Решение пределов с квадратными уравнениямиуже является простейшим множителем, и упростить его никак нельзя.

Решение пределов с квадратными уравнениями

Очевидно, что можно сократить на 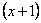Решение пределов с квадратными уравнениями:

Решение пределов с квадратными уравнениями

Теперь и подставляем -1 в выражение, которое осталось под знаком предела:

Решение пределов с квадратными уравнениями

Естественно, в контрольной работе, на зачете, экзамене так подробно решение никогда не расписывают. В чистовом варианте оформление должно выглядеть примерно так:

Решение пределов с квадратными уравнениями

Разложим числитель на множители.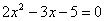
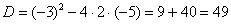
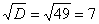
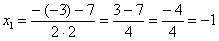
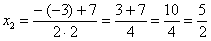
Решение пределов с квадратными уравнениями
Решение пределов с квадратными уравнениями
Решение пределов с квадратными уравнениями
Решение пределов с квадратными уравнениями
Решение пределов с квадратными уравнениями
Решение пределов с квадратными уравнениями

Решение пределов с квадратными уравнениями

Вычислить предел Решение пределов с квадратными уравнениями

Сначала «чистовой» вариант решения

Решение пределов с квадратными уравнениями

Разложим числитель и знаменатель на множители.

Числитель: 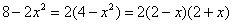Решение пределов с квадратными уравнениями
Знаменатель: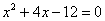
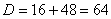
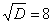
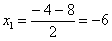
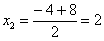
Решение пределов с квадратными уравнениями
Решение пределов с квадратными уравнениями
Решение пределов с квадратными уравнениями
Решение пределов с квадратными уравнениями, Решение пределов с квадратными уравнениями
Решение пределов с квадратными уравнениями

Решение пределов с квадратными уравнениями

Что важного в данном примере?
Во-первых, Вы должны хорошо понимать, как раскрыт числитель, сначала мы вынесли за скобку 2, а затем использовали формулу разности квадратов. Уж эту-то формулу нужно знать и видеть.

Рекомендация: Если в пределе (практически любого типа) можно вынести число за скобку, то всегда это делаем.
Более того, такие числа целесообразно выносить за значок предела. Зачем? Да просто чтобы они не мешались под ногами. Главное, потом эти числа не потерять по ходу решения.

Обратите внимание, что на заключительном этапе решения я вынес за значок предела двойку, а затем – минус.

! Важно
В ходе решения фрагмент типа Решение пределов с квадратными уравнениямивстречается очень часто. Сокращать такую дробь нельзя. Сначала нужно поменять знак у числителя или у знаменателя (вынести -1 за скобки).
Решение пределов с квадратными уравнениями, то есть появляется знак «минус», который при вычислении предела учитывается и терять его совсем не нужно.

Вообще, я заметил, что чаще всего в нахождении пределов данного типа приходится решать два квадратных уравнения, то есть и в числителе и в знаменателе находятся квадратные трехчлены.

Метод умножения числителя и знаменателя на сопряженное выражение

Продолжаем рассматривать неопределенность вида Решение пределов с квадратными уравнениями

Следующий тип пределов похож на предыдущий тип. Единственное, помимо многочленов, у нас добавятся корни.

Найти предел Решение пределов с квадратными уравнениями

Сначала пробуем подставить 3 в выражение под знаком предела
Еще раз повторяю – это первое, что нужно выполнять для ЛЮБОГО предела. Данное действие обычно проводится мысленно или на черновике.

Решение пределов с квадратными уравнениями

Получена неопределенность вида 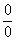Решение пределов с квадратными уравнениями, которую нужно устранять.
Решение пределов с квадратными уравнениями

Как Вы, наверное, заметили, у нас в числителе находится разность корней. А от корней в математике принято, по-возможности, избавляться. Зачем? А без них жизнь проще.

Когда в числителе (знаменателе) находится разность корней (или корень минус какое-нибудь число), то для раскрытия неопределенности 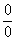Решение пределов с квадратными уравнениямииспользуют метод умножения числителя и знаменателя на сопряженное выражение.

Вспоминаем нашу нетленную формулу разности квадратов: 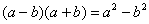Решение пределов с квадратными уравнениями
И смотрим на наш предел: 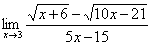Решение пределов с квадратными уравнениями
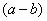
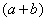
Что можно сказать? Решение пределов с квадратными уравнениямиу нас в числителе уже есть. Теперь для применения формулы осталось организовать Решение пределов с квадратными уравнениями(которое и называется сопряженным выражением).

Умножаем числитель на сопряженное выражение:

Решение пределов с квадратными уравнениями

Обратите внимание, что под корнями при этой операции мы ничего не трогаем.

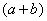
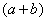
Хорошо, Решение пределов с квадратными уравнениямимы организовали, но выражение-то под знаком предела изменилось! А для того, чтобы оно не менялось, нужно его разделить на то же самое, т.е. на Решение пределов с квадратными уравнениями:

Решение пределов с квадратными уравнениями

То есть, мы умножили числитель и знаменатель на сопряженное выражение.
В известной степени, это искусственный прием.

Умножили. Теперь самое время применить вверху формулу 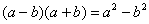Решение пределов с квадратными уравнениями:

Решение пределов с квадратными уравнениями

Неопределенность 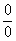Решение пределов с квадратными уравнениямине пропала (попробуйте подставить тройку), да и корни тоже не исчезли. Но с суммой корней всё значительно проще, ее можно превратить в постоянное число. Как это сделать? Да просто подставить тройку под корни:

Решение пределов с квадратными уравнениями

Число, как уже отмечалось ранее, лучше вынести за значок предела.

Теперь осталось разложить числитель и знаменатель на множители, собственно, это следовало сделать раньше.
Решение пределов с квадратными уравнениями

Как должно выглядеть решение данного примера в чистовом варианте?
Примерно так:

Решение пределов с квадратными уравнениями

Умножим числитель и знаменатель на сопряженное выражение.

Решение пределов с квадратными уравнениями

Найти предел Решение пределов с квадратными уравнениями

Сначала попробуйте решить его самостоятельно.

Окончательное решение примера может выглядеть так:

Решение пределов с квадратными уравнениями

Разложим числитель на множители: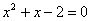
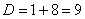
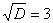
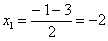
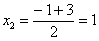
Решение пределов с квадратными уравнениями
Решение пределов с квадратными уравнениями
Решение пределов с квадратными уравнениями
Решение пределов с квадратными уравнениями
Решение пределов с квадратными уравнениями
Решение пределов с квадратными уравнениями

Умножим числитель и знаменатель на сопряженное выражение

Видео:Вычислить предел. Пример 1.Скачать

Вычислить предел. Пример 1.

Предел по-шагам

Видео:27. Вычисление предела функции №1. Примеры 1-4Скачать

27. Вычисление предела функции №1. Примеры 1-4

Результат

Примеры пределов

  • Пределы от рациональных дробей на бесконечности
  • Пределы от рациональных дробей в конечной точке
  • Пределы от дроби в нуле
  • Первый замечательный предел
  • Второй замечательный предел
  • Пределы с квадратными корнями
  • Правило Лопиталя

Указанные выше примеры содержат также:

  • квадратные корни sqrt(x),
    кубические корни cbrt(x)
  • тригонометрические функции:
    синус sin(x), косинус cos(x), тангенс tan(x), котангенс ctan(x)
  • показательные функции и экспоненты exp(x)
  • обратные тригонометрические функции:
    арксинус asin(x), арккосинус acos(x), арктангенс atan(x), арккотангенс actan(x)
  • натуральные логарифмы ln(x),
    десятичные логарифмы log(x)
  • гиперболические функции:
    гиперболический синус sh(x), гиперболический косинус ch(x), гиперболический тангенс и котангенс tanh(x), ctanh(x)
  • обратные гиперболические функции:
    asinh(x), acosh(x), atanh(x), actanh(x)
  • число Пи pi
  • комплексное число i

Правила ввода

Можно делать следующие операции

2*x — умножение 3/x — деление x^3 — возведение в степень x + 7 — сложение x — 6 — вычитание Действительные числа вводить в виде 7.5, не 7,5

Чтобы увидеть подробное решение,
помогите рассказать об этом сайте:

🌟 Видео

31. Вычисление пределов функций. Неопределенность 0/0 с корнями разных степенейСкачать

31. Вычисление пределов функций. Неопределенность 0/0 с корнями разных степеней

36. Вычисление пределов функций с использованием 2-го замечательного пределаСкачать

36. Вычисление пределов функций с использованием 2-го замечательного предела

28. Вычисление пределов функций №2. Неопределенность 0/0, заданная отношением двух многочленов.Скачать

28. Вычисление пределов функций №2. Неопределенность 0/0, заданная отношением двух многочленов.

29. Вычисление пределов функции №4. Неопределенность 0/0 с корнями.Скачать

29. Вычисление пределов функции №4. Неопределенность 0/0 с корнями.

Предел функции на бесконечности. 10 класс.Скачать

Предел функции на бесконечности. 10 класс.

Алгебра 8 класс (Урок№29 - Решение задач с помощью квадратных уравнений.)Скачать

Алгебра 8 класс (Урок№29 - Решение задач с помощью квадратных уравнений.)

5 способов решения квадратного уравнения ➜ Как решать квадратные уравнения?Скачать

5 способов решения квадратного уравнения ➜ Как решать квадратные уравнения?

Вычисление пределов #2Скачать

Вычисление пределов #2

30. Вычисление предела функции. Неопределенность 0/0 с корнямиСкачать

30. Вычисление предела функции. Неопределенность 0/0 с корнями

Решение квадратных уравнений. Дискриминант. 8 класс.Скачать

Решение квадратных уравнений. Дискриминант. 8 класс.

Математика без Ху!ни. Пределы, часть1. Неопределенность, раскрытие неопределенностей.Скачать

Математика без Ху!ни. Пределы, часть1. Неопределенность, раскрытие неопределенностей.

33. Вычисление пределов функций. Первый замечательный пределСкачать

33. Вычисление пределов функций. Первый замечательный предел

11. Вычисление предела последовательности ( предел отношения двух многочленов ), примеры 1 и 2.Скачать

11. Вычисление предела последовательности ( предел отношения двух многочленов ), примеры 1 и 2.

18. Вычисление предела последовательности. Бесконечность минус бесконечность. Примеры 16, 17,18.Скачать

18. Вычисление предела последовательности. Бесконечность минус бесконечность. Примеры 16, 17,18.

13. Вычисление предела последовательности ( предел с корнями и степенями ), примеры 5 и 6.Скачать

13. Вычисление предела последовательности ( предел с корнями и степенями ), примеры 5 и 6.

Вычисление пределов #1Скачать

Вычисление пределов #1

Вычисление пределов #10Скачать

Вычисление пределов #10
Поделиться или сохранить к себе: