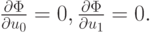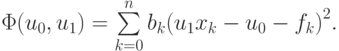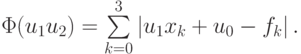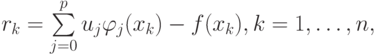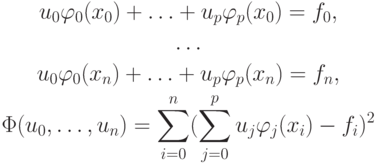Решение переопределенной системы линейных уравнений (4 видео)

Численное решение переопределенных СЛАУ. Метод наименьших квадратов

Содержание

3.1. Пример использования метода наименьших квадратов (МНК)
Решение переопределенной системы линейных уравнений
Решение систем линейных уравнений
💡 Видео

3.1. Пример использования метода наименьших квадратов (МНК)

Приведем простой пример получения переопределенной системы линейных уравнений. Такого рода задачи часто встречаются, например, при обработке результатов экспериментов.

Пусть f — линейная (или близкая к линейной) функция аргумента x : f(x) = u₁x + u₀ . В точках x_k известны значения функции f(x_k) . Тогда u₀, u₁ — коэффициенты , которые необходимо подобрать так, чтобы выполнялись условия u₁x_k + u₀ = f_k , k = 0,1,2,3,4, f_k = f(x_k) .

Получим систему пяти уравнений относительно двух неизвестных. Это — переопределенная система . Она не имеет классического решения, так как в общем случае не существует прямой , проходящей через все 5 точек (это возможно только тогда, когда какие — либо три уравнения полученной системы линейными преобразованиями сводятся к двум другим — система линейно зависима).

Рассмотрим общий случай. Пусть коэффициенты <u₀, u₁> необходимо определить по результатам n + 1 измерения. Введем функцию, равную сумме квадратов невязок r_k = u₁x_k + u₀ — f_k

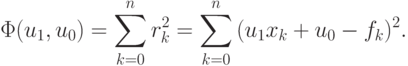Решение переопределенной системы линейных уравнений

( 3.1)

Примем за обобщенное решение переопределенной СЛАУ такие <u₀, u₁> для которых 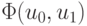принимает наименьшие значение . Для определения обобщенного решения из условия минимума суммы квадратов невязки получаем систему двух уравнений, имеющую классическое решение:

Выбор функции 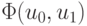имеет некоторый произвол. Например, возможно каждому измерению придать некоторый вес b_k . От набора таких весовых множителей зависело бы решение системы. В этом случае функция будет

Если в качестве невязки выбрать r_k = | u₁x_k + u₀ — f_k | , то получим задачу линейного программирования на отыскании минимума функции

Получившийся таким образом функционал, вообще говоря, не дифференцируем. Для решения задачи нельзя использовать метод наименьших квадратов .

Произвол имеется и в выборе базисных функций. Вообще говоря, можно было бы записать невязку r_k в виде

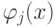
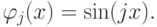
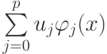
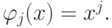
где — некоторые функции, образующие базис , например, тригонометрические: Выражение называется обобщенным полиномом. В приведенном выше примере в качестве базисных функций были выбраны степенные функции Обобщенный полином превратился в алгебраический.

В случае выбора произвольной системы базисных функций переопределенная СЛАУ и функционал 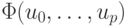будут

Отыщем обобщенное решение методом наименьших квадратов . Приравнивая все частные производные по компонентам обобщенного решения к нулю

Видео:Метод Крамера за 3 минуты. Решение системы линейных уравнений - bezbotvyСкачать

Решение переопределенной системы линейных уравнений

Система линейных уравнений у которой к-во уравнений ( n ) больше, чем к-во неизвестных ( m ) называется переопределённой. В этом случае чаще всего решения не существует, поэтому под решением подразумевают такие значения неизвестных, которые минимизируют некоторую норму вектора невязок.
При использовании p-норм условие задачи можно записать в виде: где A — это матрица коэффициентов ( n * m ), x — вектор решения ( m ), b — вектор свободных членов ( n ).
Обычно используется 2-норма, что приводит к методу наименьших квадратов. Эта норма обладает многими хорошими свойствами ( простота реализации, единственность и непрерывность решения ), но в некоторых случаях предпочтительнее другие нормы. Например, при использовании 1-нормы решение менее подвержено влиянию шумов ( неточные исходные данные ). Решение этой задачи ( которое может быть не единственным ) заключается в выборе из этой системы m уравнений, решение которых будет минимизировать вектор невязок исходной системы. Назовём эти уравнения главными.
Следующие функции находят решение с минимальной 1-нормой: Здесь data — это двухмерный массив ( n * (m+1) ) с исходными данными, в последнем столбце которого записан вектор b, x — ссылка на массив решения, index — ссылка на массив в который запишутся индексы главных уравнений. В этих функциях вначале определяются главные уравнения, а затем, если нужно, по ним методом исключений ( или Гаусса ) находится решение х.

Следующая функция находит решение с минимальной 2-нормой: Здесь вначале строится система нормальных уравнений, а затем она решается методом Гаусса.

При использовании бесконечной нормы минимизируется максимальное значение невязок. Следующие функции находят решение с минимальной ∞-нормой: Эти функции определяют m + 1 главных уравнений, для которых невязки будут равны максимальному значению, а для остальных уранений невязки будут меньше или равны максимальному значению.

Видео:Решение системы линейных уравнений с двумя переменными способом подстановки. 6 класс.Скачать

Решение систем линейных уравнений

Эта страничка поможет решить Системы Линейных Алгебраических Уравнений (СЛАУ) методом Гаусса, матричным методом или методом Крамера, исследовать их на совместность (теорема Кронекера-Капелли), определить количество решений, найти общее, частное и базисные решения.

Введите коэффициенты при неизвестных в поля. Если Ваше уравнение имеет меньшее количество неизвестных, то оставьте пустыми поля при переменных, не входящих в ваше уравнение. Можно использовать дроби ( 13/31 ).