Решение однородных уравнений с подробным решением

Видео:Решение тригонометрических уравнений. Однородные уравнения. 10 класс.Скачать

Определение

Видео:4. Однородные дифференциальные уравнения (часть 1)Скачать

Как определить однородное дифференциальное уравнение

Для того, чтобы определить, является ли дифференциальное уравнение первого порядка однородным, нужно ввести постоянную t и заменить y на ty и x на tx : y → ty , x → tx . Если t сократится, то это однородное дифференциальное уравнение. Производная y′ при таком преобразовании не меняется.
.

Пример

Определить, является ли данное уравнение однородным

Делаем замену y → ty , x → tx .

Делим на t 2 .

.
Уравнение не содержит t . Следовательно, это однородное уравнение.

Видео:15. Однородная система линейных уравнений / фундаментальная система решенийСкачать

Метод решения однородного дифференциального уравнения

Однородное дифференциальное уравнение первого порядка приводится к уравнению с разделяющимися переменными с помощью подстановки y = ux . Покажем это. Рассмотрим уравнение:
(i)
Делаем подстановку:
y = ux ,
где u — функция от x . Дифференцируем по x :
y′ = ( ux ) ′ = u′ x + u ( x ) ′ = u′ x + u
Подставляем в исходное уравнение (i).
,
,
(ii) .
Разделяем переменные. Умножаем на dx и делим на x ( f ( u ) – u ) .

При f ( u ) – u ≠ 0 и x ≠ 0 получаем:

Интегрируем:

Таким образом, мы получили общий интеграл уравнения (i) в квадратурах:

Заменим постоянную интегрирования C на ln C , тогда

Опустим знак модуля, поскольку нужный знак определяется выбором знака постоянной C . Тогда общий интеграл примет вид:

Далее следует рассмотреть случай f ( u ) – u = 0 .
Если это уравнение имеет корни, то они являются решением уравнения (ii). Поскольку уравнение (ii) не совпадает с исходным уравнением, то следует убедиться, что дополнительные решения удовлетворяют исходному уравнению (i).

Всякий раз, когда мы, в процессе преобразований, делим какое-либо уравнение на некоторую функцию, которую обозначим как g ( x, y ) , то дальнейшие преобразования справедливы при g ( x, y ) ≠ 0 . Поэтому следует отдельно рассматривать случай g ( x, y ) = 0 .

Видео:Дифференциальные уравнения, 3 урок, Однородные уравненияСкачать

Пример решения однородного дифференциального уравнения первого порядка

Проверим, является ли данное уравнение однородным. Делаем замену y → ty , x → tx . При этом y′ → y′ .
,
,
.
Сокращаем на t .

Постоянная t сократилась. Поэтому уравнение является однородным.

Делаем подстановку y = ux , где u – функция от x .
y′ = ( ux ) ′ = u′ x + u ( x ) ′ = u′ x + u
Подставляем в исходное уравнение.
,
,
,
.
При x ≥ 0 , |x| = x . При x ≤ 0 , |x| = – x . Мы пишем |x| = ± x подразумевая, что верхний знак относится к значениям x ≥ 0 , а нижний – к значениям x ≤ 0 .
,
Умножаем на ± dx и делим на .

При u 2 – 1 ≠ 0 имеем:

Интегрируем:

Интегралы табличные,
.

Применим формулу:
( a + b )( a – b ) = a 2 – b 2 .
Положим a = u , .
.
Возьмем обе части по модулю и логарифмируем,
.
Отсюда
.

Таким образом имеем:
,
.
Опускаем знак модуля, поскольку нужный знак обеспечивается выбором знака постоянной C .

Умножаем на x и подставляем ux = y .
,
.
Возводим в квадрат.
,
,
.

Теперь рассмотрим случай, u 2 – 1 = 0 .
Корни этого уравнения
.
Легко убедиться, что функции y = ± x удовлетворяют исходному уравнению.

Использованная литература:
Н.М. Гюнтер, Р.О. Кузьмин, Сборник задач по высшей математике, «Лань», 2003.

Автор: Олег Одинцов . Опубликовано: 19-07-2012 Изменено: 24-02-2015

Видео:18+ Математика без Ху!ни. Дифференциальные уравнения. Однородное уравнение.Скачать

Однородные уравнения и неравенства

Однородные уравнения – это уравнения, в которых все слагаемые имеют одинаковую суммарную степень.

Однородные неравенства – это неравенства, в которых все слагаемые имеют одинаковую суммарную степень.

Пример. Решить уравнение (sin⁡x=sqrtcos⁡x).

Перед нами типичное однородно-тригонометрическое уравнение. Надо разделить уравнение на cos⁡x, но делить на число равное нулю нельзя, поэтому проверим, является ли (cos⁡x=0) решением уравнения. Если (cos⁡x=0), то (sin⁡x=±1). Очевидно, что (±1≠0).

Теперь с чистой совестью поделим уравнение на (cos⁡x)

Заметьте, что в этом примере перед тем, как делить на (cos⁡x), была сделана проверка — является ли (cos⁡x=0) решением уравнения. Нужно каждый раз проверять, является ли выражение, на которое вы хотите поделить, решением. Иначе вы рискуете потерять корни уравнения .

Пример. Решить уравнение (7cdot 9^+5cdot 6^-48cdot 4^=0).

Показатели степеней в уравнении похожи – в каждом есть (x^2-3x). Давайте сделаем их одинаковыми.
Представим (48cdot 4^) как (12cdot 4^1cdot 4^).

Получился классический вид однородного уравнения.
Поделим уравнение на (4^) .
Положительное число в степени никогда не будет равно нулю, поэтому проверку можно не делать.

Обратите внимание: ((frac)^2) (=) (frac) . С учетом этого сделаем замену.

Положительное число в любой степени всегда больше нуля, поэтому (t>0). Отметим это в решении, чтобы не забыть.

Видео:Однородное уравнение в системеСкачать

Однородные уравнения

Однородные уравнения

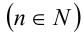Алгебраический многочлен f(x,y) с двумя переменными x и у называется однородным многочленом n -й степени относительно этих переменных , если при любом 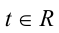имеет место тождество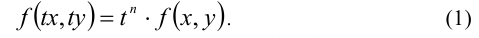

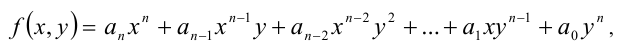
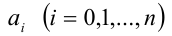Это означает, что однородный многочлен n-й степени f (х, у) можно представить в виде

где — коэффициенты многочлена, одновременно не обращающиеся в нуль.

Уравнение f(x,y) = 0 называется однородным алгебраическим уравнением n -й степени с двумя неизвестными x,у, если f(x,y) — однородный многочлен n-й степени относительно этих переменных.

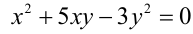Например, уравнение вида является однородным уравнением 2-й степени относительно неизвестных x и у . Действительно, достаточно проверить выполнение условия (1). При одновременной замене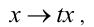 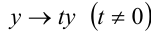, получим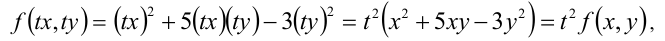

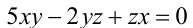т.е. условие (1) из определения выполняется (n = 2).

Аналогично, уравнение есть однородное уравнение 2-й степени по отношению к неизвестным x,y,z , поскольку при замене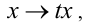 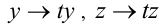получаем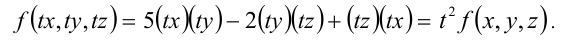

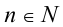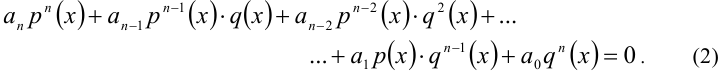
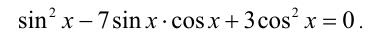
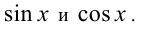
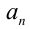Итак, однородное алгебраическое уравнение — это уравнение, не меняющее своего вида при одновременном умножении всех его неизвестных на одно и то же число, отличное от нуля. Можно распространить понятие однородности на случай неалгебраических уравнений.

Пусть р(х) и q(x) — две произвольные функции, определённые на одном и том же множестве, .

Однородным уравнением n -й степени относительно функций р(х), q(x) называется уравнение вида

В частности, если функции р(х) и q(x) являются целыми алгебраическими многочленами, то и уравнение (2) будет относиться к аналогичному классу. В качестве другого примера рассмотрим уравнение вида

Оно является однородным тригонометрическим уравнением 2-й степени относительно функций

Перейдём к процедуре решения уравнения (2).

Если хотя бы один из коэффициентов или 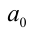обращается в нуль, то левая часть уравнения легко раскладывается на множители. В результате уравнение оказывается равносильно на ОДЗ совокупности двух уравнений. Например, если 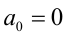, 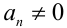то получим совокупность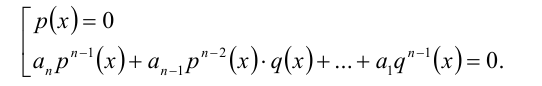

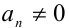Если же и 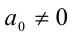, то для решения однородного уравнения (2) необходимо рассмотреть два возможных случая.

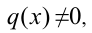1) Если то, поделив обе части уравнения на 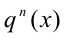и обозначив после этого отношение p(x)/q(x) через t , получим алгебраическое уравнение n -й степени относительно t: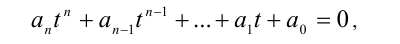

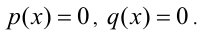
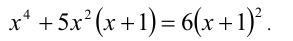
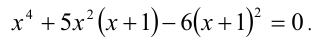решив которое и сделав обратную подстановку, найдём часть решений однородного уравнения.

2) Если q(х) = 0. то, подставив в уравнение вместо q(x) нуль, получим, что тогда и р(х) должно обращаться в нуль. Таким образом, этот случай сводится к решению системы уравнений

Осталось объединить все найденные решения. Уравнение (2) решено. Обратимся к примерам.

Пример №185.

Решить уравнение

Решение:

Перепишем уравнение: Видно, что это однородное уравнение 2-й степени относительно функци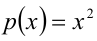й и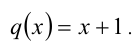1) Пусть х + 1 = 0 , но система 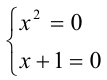решений не имеет.

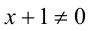2) Пусть теперь . Поделив на 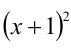и обозначив 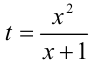, придём к квадратному уравнению 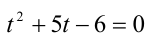. Оно имеет два корня 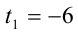, 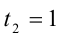. Возвращаясь к переменной x , приходим к совокупности двух уравнений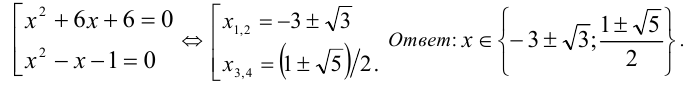

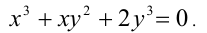
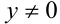Пример №186.

Решить в целых числах уравнение

Решение:

Заметим, что если у = 0, то x = 0, и, значит, пара (0;0) удовлетворяет уравнению. Пусть , тогда поделим обе части уравнения на :

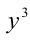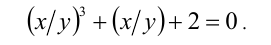
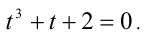Обозначим t = x/у, тогда имеем кубическое уравнение Подбором находим корень t = — 1. Делением многочлена 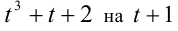получаем: 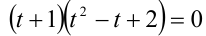Убеждаемся в том, что данное кубическое уравнение имеет единственный корень t = — 1, что соответствует у = — x . Положим x = р, где р — произвольное целое число, не равное 0. Тогда у = — р , и имеем бесконечно много решений в виде пар чисел (р;- р), 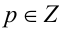, 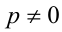. Объединяя все полученные решения, приходим к ответу.

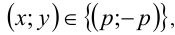Ответ: где .

Пример №187.

Для каждого действительного значения параметра а решить уравнение

Решение:

Заметим, что данное уравнение можно рассмотреть как однородное алгебраическое уравнение 4-й степени относительно x и а.

1) Если а = 0 , то х = 0 .

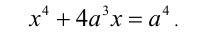
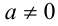2) Если , то поделим на 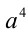, и положим :

Первый сомножитель в нуль не обращается, а второй имеет два корня

Ответ: при а = 0 единственное решение x = 0 ;

при два решения

Пример №188.

Найти действительные корни уравнения

Решение:

Данное уравнение в исходном виде не является однородным, но может быть сведено преобразованиями к однородному. Действительно, достаточно привести его к виду

Получили однородное уравнение 2-й степени относительно x + 1 и у — 1.

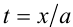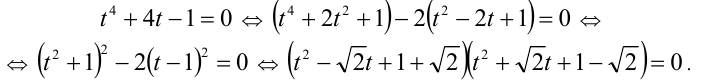
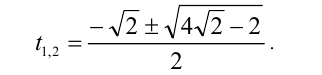
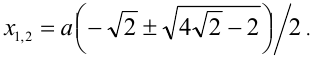
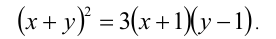
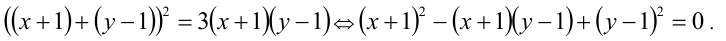
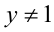1) Если , то, поделив на 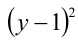и обозначив 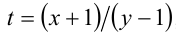, получим 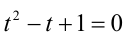нет решений.

2) Если у = 1, то, подставляя в уравнение, находим x = — 1 .

Ответ:

Эта лекция взята со страницы, где размещён подробный курс лекций по предмету математика:

Эти страницы возможно вам будут полезны:

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

🌟 Видео

§41 Решение систем линейных однородных уравненийСкачать

Видеоурок "Однородные системы линейных уравнений"Скачать

Простейшие тригонометрические уравнения. y=sinx. 1 часть. 10 класс.Скачать

Дифференциальные уравнения 1-го порядка.Скачать

Математика без Ху!ни. Метод Гаусса.Скачать

Простая, но очень противная задача на окружности из ЕГЭ | Планиметрия 83 | mathus.ru #егэ2024Скачать

10 класс, 23 урок, Методы решения тригонометрических уравненийСкачать

9 класс, 12 урок, Однородные системы. Симметрические системыСкачать

Однородное дифференциальное уравнениеСкачать

6. Дифференциальные уравнения, приводящиеся к однороднымСкачать

Однородное уравнениеСкачать

Решение тригонометрических уравнений. Подготовка к ЕГЭ | Математика TutorOnlineСкачать

Задача Коши ➜ Частное решение линейного однородного дифференциального уравненияСкачать