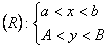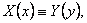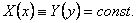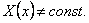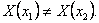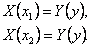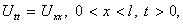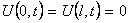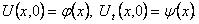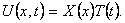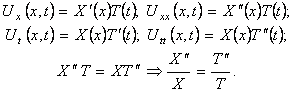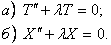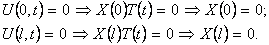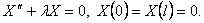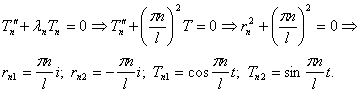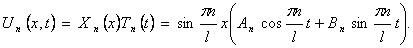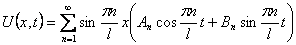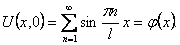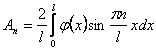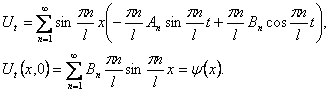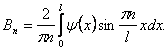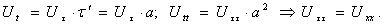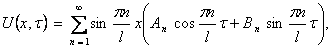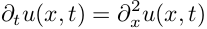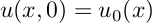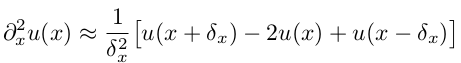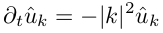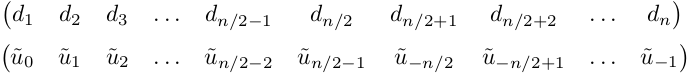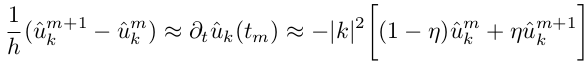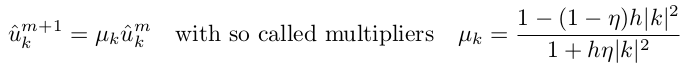Решение одномерного волнового уравнения методом фурье (4 видео)

Лекция 3. Метод Фурье

Метод Фурье — один из распространенных и эффективных методов решения уравнений с частными производными. Этот метод часто встречается и под другими названиями: метод разделения переменных или метод собственных функций.

Содержание

Общая схема метода Фурье.
Основная лемма метода Фурье.
Решение первой начально-краевой задачи для волнового уравнения.
Метод Фурье
Метод Фурье
Первое из граничных условий
Спектральный метод на примере простых задач матфизики
Одномерная задача распространения тепла по стержню
Двумерное уравнение диффузии
Двумерное волновое уравнение
Выводы
💡 Видео

Общая схема метода Фурье.

Основная идея этого метода состоит в том, что решение задачи для уравнения с частными производными сводится к решению вспомогательных задач для уравнений с меньшим числом независимых переменных. В частности, если заданное уравнение содержит две независимые переменные, то вспомогательные задачи будут уже зависеть только от одной переменной. Таким образом решение уравнения с частными производными сводится к решению обыкновенных дифференциальных уравнений.

При применении метода Фурье удобно использовать следующую лемму.

Основная лемма метода Фурье.

Если в прямоугольнике R плоскости XOY:

для некоторых функций выполняется тождество

то в этом случае

Доказательство. Предположим противное, т.е. что

Тогда существуют значения 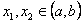такие, что

Рассмотрим точки (x₁,y) и (x₂,y), принадлежащие прямоугольнику R. На R справедливо тождество (8), а поэтому

Сравнивая эти равенства, приходим к противоречию с нашим предположением. Следовательно X(x) = const, а тогда Y(y)=const.

Решение первой начально-краевой задачи для волнового уравнения.

Рассмотрим волновое уравнение

Граничные условия первого рода

И начальные условия

Решим эту задачу методом Фурье.

Шаг 1. Представим функцию U(x,t) в виде

Найдем частные производные U_xx и U_tt и подставим в уравнение (9):

В полученном уравнении левая часть зависит только от x, а правая- только от t. Используя основную лемму, заключаем:

Из граничных условий (10) получим

Шаг 2. Решим задачу Штурма-Лиувилля

Она имеет собственные значения и собственные функции

Шаг 3. Подставим найденные значения λ_n в уравнение а) и решим его:

Шаг 4. Выпишем частные решения уравнения (9):

Для волнового уравнения эти решения называются собственными колебаниями. В лекции 6 мы изучим их подробнее. В силу линейности и однородности уравнения (9) линейная комбинация этих решений

Замечание 1. Здесь мы предполагаем, что полученный функциональный ряд равномерно сходится и его можно дважды почленно дифференцировать по x и по t в области 0 0. Об условиях, при которых это можно сделать, будет рассказано в лекции 5.

Шаг 5. Определим коэффициенты A_nи B_n в формуле (12), используя начальные условия (11). Из первого начального условия получим

Равенство (13) означает, что начальная функция φ(x) разлагается в ряд Фурье по синусам, которые в данном случае являются собственными функциями X_n(x) задачи Штурма-Лиувилля.

Коэффициенты Фурье вычисляются по формулам

Из второго начального условия находятся коэффициенты B_n.

Вычислив коэффициенты A_n и B_n для конкретных начальных функций и подставив их значения в (12), мы получим решение первой начально-краевой задачи.

Замечание 2. Используя формулу (12), можно получить решение первой начально-краевой задачи для уравнения колебания струны: Для этого проведем замену переменной τ=at и получим

При этом начальное условие не изменится, а условие преобразуется к виду Тогда решение задачи в переменных (x,τ) будет иметь вид

Возвращаясь к переменным (x,t), получим

Видео:Уравнение колебаний струны. Метод разделения переменных. Метод ФурьеСкачать

Метод Фурье

Содержание:

По этой ссылке вы найдёте полный курс лекций по математике:

Метод Фурье, или метод разделения переменных, является одним из наиболее распространенных методов решения уравнений с частными производными. Рассмотрим этот метод, обратившись к простейшей задаче о свободных колебаниях однородной струны длины i, закрепленной на концах. §4. Свободные колебания однородной струны, закрепленной на концах Задача о свободных колебаниях однородной струны с закрепленными концами сводится к решению уравнения при граничных условиях и начальных условиях.

Метод Фурье Задачу (1 )-(3) называют смешанной: она содержит и начальные и граничные условия. Решение задачи начнем с поиска частных решений уравнения (1) вида При этом будем предполагать, что каждое из них удовлетворяет граничным условиям (2), но не равно нулю тождественно. Подставляя функцию и<х, t) в форме (4) в уравнение (1), получаем ИЛИ Последнее равенство (его левая часть зависит только от а правая — только от х) возможнолишь втом случае, если обе его части не зависят ни от ty ни от х,т.е. равны одной и той же постоянной.

Обозначим эту постоянную (разделения) через (-А), Из равенства (5) получаем два обыкновенных дифференциальных уравнения Граничные условия (2) дают откуда (T(t) £ 0) следует, что функция Х(х) должна удовлетворять граничным условиям Чтобы получить нетривиальные решения tt(x, t) вида (4), удовлетворяющие граничным условиям (2), необходимо найти нетривиальные решения уравнения удовлетворяющие граничным условиям.

Таким образом, мы приходим к следующей задаче: найти значения параметра А, при которых существуют нетривиальные решения задачи (7)-(8), а также сами эти решения. Такие значения параметра А называются собственными значениями, а соответствующие им нетривиальные решения — собственными функциями задачи (7)-(8). Сформулированную таким образом задачу называют задачей Штурма—Лиувилля. Найдем собственные значения и собственные функции задачи (7)-(8).

Рассмотрим отдельно три случая, когда 1.

При общее решение уравнения (7) имеет вид Потребовав выполнения граничных условий (8), получим (6) (7) Так как определитель системы (9) отличен от нуля, то . Следовательно, Х(х) = 0, т. е. при нетривиальных решений задачи не существует. (9) 2. При А = 0 общее решение уравнения (7) имеет вид Граничные условия (8) дают откуда С, = С2 = 0, и следовательно, при А = 0 нетривиальных решений задачи (7)-(8) также не существует. 3.

При Л > 0 общее решение уравнения (7) имеет вид Потребовав выполнение граничных условий (8), получим Система (10) имеет нетривиальные решениятогда и толькотогда, когда определитель системы равен нулю, Метод Фурье будут собственными функциями задачи. Собственные функции определены с точностью до постоянного множителя, который мы выбрали равным единице. При А = А* общее решение у равнения (6) имеетвид ктга кчга где Аки Bk — произвольные постоянные. Таким образом, функции удовлетворяют уравнению (1) и граничным условиям (2) при любых Ак и Вку В силу линейности и однородности уравнения (1) всякая коневая сумма решений будет также решением уравнения (1).

То же справедливо и для ряда если он сходится равномерно и его можно дважды почленно дифференцировать по х и по t. Поскольку каждое слагаемое в ряде (11) удовлетворяет граничным условиям (2), то этим условиям будет удовлетворять и сумма u(s, t) этого ряда. Остается определить в формуле (11) постоянные .4* и Вк так, чтобы выполнялись и начальные условия (3). Продифференцируем формально ряд (11) по t.

Имеем Полагая в соотношениях (l 1) и (12) t = 0, в силу начальных условий (3) получим Формулы (13) представляют собой разложения заданных функций вряд Фурье по синусам в интервале Коэффициенты разложений (13) вычисляются по известным формулам / I Теорема 2. Если и удоъчетворяет условиям и удовлетворяет условию то сумма tx(x, £) ряда (11), где -А* и В* опредыяются формулами (14), имеет в области непрерывные частные производные до второго порядка включительно по каждому из аргументов, удовлетворяет уравнению (1), граничным условиям (2) и начальным условиям (3), т. е. является решением задачи (1 )-(3).

Пример. Найти закон свободных колебаний однородной струны длины I, закрепленной на концах, если в начальный момент t = 0 струна имеет форму параболы — const), а начальная скорость отсутствует. 4 Задача сводится к решению уравнения при граничных условиях и начальных условиях.

Возможно вам будут полезны данные страницы:

Метод Фурье

Применяя метод Фурье, ищем нетривиальные решения уравнения (1), удовлетворяющие граничным условиям (2), в виде Подставляя «(*,*) в форме (4) в уравнение (1) и разделяя переменные, получим откуда причем в силу (2) Как было установлю но выше, собственные значения задачи (7)-(8) а соответствующие собственные функции Для А = Ащ общее решение уравнения (6) имеет вид пяа ижа Будем иска тъ решение исходной задачи в виде ряда Для определен ия коэффициентов -4Я и Z?„ воспользуемся начальными условия ми (3).

Имеем Из формулы (II) срезу

получаем, что 2?„ = 0 для любог о п, а из (10) Метод Фурье откуда, интегрируя по частям дважды . находи м . Подставляя наеденные значения А, и в ряд (9), получим решение поставленной задачи , Замечание. Если начальные фукхдда не удовлетворяют условиям теоремы 2, то дважды непрерывно дифференцируемого решения смешанной задачи (1)-(3) может и не существовать.

Однако если , то ряд (II) сходетс* равномерно при и любом t и определяет непрерывную функюао u(xtt). В этом случае можно говорить лишь об обобщенная решении задачи. Каждая из функций определяет так называемые собств енные колебания струны, закрепленной на концах. При собственных колебаниях, отвечающих к = 1, струна издает основной, самый низкий тон.

При колебаниях, соответствующих ббльшим Л.она издает более высокие тоны, обертоны. Записав *) в виде заключаем, что собственные колебания струны — стоячие волны, при которых точки струны совершают гармонические колебания с амплитудой Нк sin частотой Метод Фурье Мы рассмотрели случай свободных колебаний однородной струны, закрепленной на концах. Рассмотрим теперьслуч ай других граничных условий.

Пусть, например, левый конец струны закреплен, u(0, t) = 0, а правый конец х — 1 упругосвязан со своим положением равновесия, что соответствует условию . Нетривиальное решение u(x, t) уравнения (1), удовлетворяющее поставленным граничным условиям, будем опять искать в виде В результате подстановки в уравнение (1) приходим к следующей задаче о собственных значениям: найти такие значения параметра Л, для которых дифференциальное уравнение при граничных условиях имеет нетривиальные решения Х(х). Общее решение уравнения (15) имеет вид (А > 0)

Первое из граничных условий

Первое из граничных условий (16) дает С = 0, так что функциями Х(х) с точностью до постоянного множителя являются sin у/Хх. Из второго граничного условия Положим А = ir. Тогда Для отыскания и получаем трансцендентное уравнение. Корни этого уравнения можно найти графически, взяв в плоскости (f, z) сечения последовательных ветвей кривой z = tg(i//) прямой линией z = (рис. 7).

Обе части уравнения (18) — нечетные функции относительно р, поэтому каждому положительному корню i/fc соответствует равный ему по абсолютной величине отрицательный корень. Поскольку изменение знака Uk не влечет за собой появления новых собственных функций (они только изменят знак, что несущественно), достаточно ограничиться положительными корнями уравнения (18).

В результате опять получается последовательность собственных значений и отвечающие им последовательности собственных функций и собственных колебаний Кстати, для n-ой собственной частоты ип получается асимптотическое соотношение в частности, для I = т имеем Если правый конец струны х = I свободен, получаем cos vl = 0. Отсюда ul = § + тиг, так что в случае свободного конца собственные значения и собственные функции соответственно равны

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.

Видео:5. Решение волнового уравнения на отрезке методом ФурьеСкачать

Спектральный метод на примере простых задач матфизики

В этой статье описан псевдоспектральный метод численного решения уравнений матфизики, используемый в вычислительной гидродинамике, геофизике, климатологии и во многих других областях.

Одномерная задача распространения тепла по стержню

Для начала рассмотрим простую одномерную задачу распространения тепла в стержне. Уравнение, описывающее распространение тепла при некотором начальном распределении температуры по стержню:

Такое уравнение решается аналитически методом разделения переменных, например здесь, но нас интересует как это можно сделать численно. Прежде всего нужно определиться, как считать вторую пространственную производную по х. Проще всего это делается каким-нибудь разностным методом, например:

Но мы поступим иначе. Распределение температуры есть функция координаты и времени, и в каждый момент времени эта функция может быть представлена в виде суммы ряда Фурье, который в численном виде обрезается на n-ом члене:

Где u^«с крышечкой» — это коэффициенты разложения ряда Фурье. Подставим выражение для ряда в уравнение переноса тепла:

Получаем уравнение для коэффициентов Фурье, в котором отсутствует производная по координате! Теперь это обыкновенное дифференциальное уравнение, а не в частных производных, которое можно решить простым разностным методом. Уже легче, теперь остается найти коэффициенты разложения и в этом нам очень поможет быстрое преобразование Фурье (дальше FFT).

Логика здесь следующая:

1) в начальный момент времени дана функция координаты, описывающая распределение температуры по стержню;
2) разбиваем стержень на сетку из n точек;
3) находим комплексные коэффициенты Фурье с помощью алгоритма FFT, обозначим операцию как F(u);
4) умножаем полученные коэффиценты на -|k| 2 , получаем Фурье-образ второй производной. Аналогично можно получить Фурье-образ производной более высоких порядков p, достаточно умножить на (ik) p ;
5) делаем обратное преобразование Фурье F -1 (u), с помощью алгоритма IFFT, получаем значения второй производной в точках на сетке;
6) делаем шаг по времени, уже обычной разностной, явной или неявной, схемой;
7) повторяем.

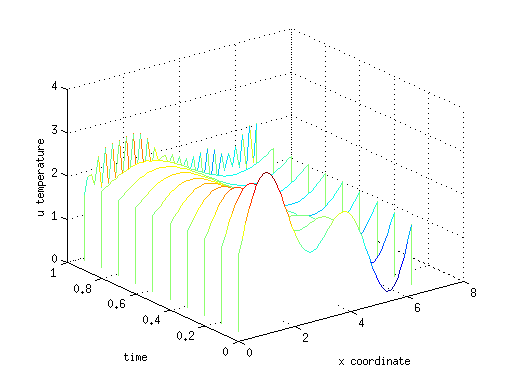
Рассмотрим теперь как это работает в программе для Matlab/Octave. В качестве начального распределения температуры возьмем гладкую функцию u0=2+sin(x)+sin(2x), стержень длинной 2π разобьем на 50 точек, с шагом по времени h=0.1, граничные условия периодичные (кольцо).

Стоит отметить особенность алгоритма FFT в Matlab, связанную с тем, что полученные коэффициенты разложения на выходе d=fft(u) идут не по порядку, а смещены, первая половина на месте второй и наоборот. Cначала идут коэффициенты с номерами от 0 до n/2-1, потом с номерами от -n/2 до -1. С этим были проблемы…

Полученное решение можно видеть на графике в виде «водопада» линий распределения температуры по х для каждого момента времени t. Видно, что решение испытывает ~~сильные осциляции~~ численную неустойчивость, связано это с невыполнением критерия Куранта. Избавиться от неустойчивости можно уменьшив шаг по времени, либо применяя более продвинутую неявную схему, например Кранка-Николсона.

Двумерное уравнение диффузии

Начальные условия: u0 = 1 + sin(2X) + cos(2Y), где u теперь 2d-массив u(i,j). Используем неявную схему интегрирования по времени (т.е. выразим m+1 шаг через m-й):

Можно доказать, что такая неявная схема никогда не расходится при η>0.5, будем использовать η=1. Таким образом каждое новое значение u m+1 получаем умножением u m на коэффициент μ_k, зависящий от временного шага и волновых чисел k, т.е. μ_k — это константа, которую не нужно пересчитывать на каждом шаге!

Двумерное волновое уравнение

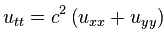
В волновом уравнении присутствует вторая производная по времени, поэтому задача сводится к системе двух обыкновенных диффуров, одна переменная — u, вторая — u_t, схему по времени в коде использовал самую простую явную, поэтому точность небольшая, шаг по времени очень маленький, зато код выглядит относительно просто. Впрочем, этого хватает для демонстрации работоспособности метода.

Периодичные граничные условия:

Фиксированные граничные условия (0 на краях, отражение волн от границ):

Выводы

В статье продемонстрировано несколько примеров применения спектрального метода для простых задач матфизики. Основная суть суть спектрального метода, это замена исходных диффренциальных уравнений в частных произодных на обыкновенные диффуры для коэффициентов разложения искомых функций по некоторому базису. Базисом могут быть синусы-косинусы, комплексные экспоненты, ортогональные полиномы, если требует геометрия — цилиндрические или сферические функции. Найденные коэффициенты в каждый момент времени позволяют восстановить искомое решение, а алгоритм FFT позволяет делать это быстро.

Преимуществами метода являются: