- Содержание
- Постановка задачи [ править ]
- Используемый метод [ править ]
- Реализация [ править ]
- Результаты [ править ]
- Научный форум dxdy
- Правила форума
- Одномерное уравнение теплопроводности. Численное решение.
- Метод Finite Volume — реализация на примере теплопроводности
- Метод Finite Volume (FVM)
- Дискретизация по времени.
- Немного теории или первый шаг в реализации FVM
- FVM на стандартной прямоугольной сетке
- Граничные условия на прямоугольной сетке
- Пример численных расчетов на прямоугольной сетке
- FVM в задачах со сложной геометрией
- Примеры и проверка результатов
- Описание структуры исходников
- 💡 Видео
Видео:Лекция №1.1 Явная и неявная схемы для уравнения теплопроводностиСкачать

Содержание
Видео:Одномерное уравнение теплопроводности. Виды краевых задачСкачать

Постановка задачи [ править ]
Необходимо решить задачу Коши для одномерного уравнения теплопроводности (дифференциальное уравнение в частных производных второго порядка, которое описывает распределение температуры в заданной области пространства и его изменение во времени.) с использованием средств параллельного программирования на основе MPI. Задача решается для однородного уравнения теплопроводности (система теплоизолирована) на промежутке [0..L]:
[math]frac — a^2frac = 0[/math]
[math]U(x,0) = U_0(x)[/math]
при следующих граничных условиях:
[math] begin U(0,t) = T_0 \ U(L,t) = T_1 end[/math]
Используемые величины параметров:
[math]L=1, T_0=0, T_1=-100[/math]
Видео:Стационарное решение одномерного уравнения теплопроводности.Скачать

Используемый метод [ править ]
В вычислительных системах с распределенной памятью процессоры работают независимо друг от друга. Для организации параллельных вычислений в таких условиях необходимо иметь возможность распределять вычислительную нагрузку и организовать информационное взаимодействие (передачу данных) между процессорами. Параллельное программирование служит для создания программ, эффективно использующих вычислительные ресурсы за счет одновременного исполнения кода на нескольких вычислительных узлах. Для создания параллельных приложений используются параллельные языки программирования и специализированные системы поддержки параллельного программирования, такие как MPI и OpenMP. Итак, MPI — это библиотека передачи сообщений, собрание функций на C/C++ (или подпрограмм в Фортране), облегчающих коммуникацию (обмен данными и синхронизацию задач) между процессами параллельной программы с распределенной памятью. Акроним MPI установлен для Message Passing Interface (интерфейс передачи сообщений). Под параллельной программой в рамках MPI понимается множество одновременно выполняемых процессов. Все процессы порождаются один раз, образуя параллельную часть программы. Каждый процесс работает в своем адресном пространстве, никаких общих переменных или данных в MPI нет. Процессы могут выполняться на разных процессорах, но на одном процессоре могут располагаться и несколько процессов (в этом случае их исполнение осуществляется в режиме разделения времени).
Видео:Метод Фурье для неоднородного уравнения теплопроводностиСкачать

Реализация [ править ]
При решении поставленной задачи будем использовать замену частных производных в дифференциальных уравнениях их разностными аналогами. Сеточный метод, основанный на замене в дифференциальном уравнении производных конечными разностями, называют методом конечных разностей, а сеточную схему такого метода — конечно-разностной.
Введем равномерную сетку [math]0 lt x_i lt L[/math] с шагом разбиения [math]Δx[/math] , [math]Δt[/math] — шаг по времени. Явная конечно-разностная схема в таком случае будет выглять следующим образом:
[math]frac<U_i^-U_i^> = a^2frac<U_^ — 2U_^+U_^>[/math]
Отрезок [0..L] разбивается на интервалы согласно количеству процессов в выполняемой параллельной программе. На каждом полученном таким способом интервале процесс интегрирования осуществляется отдельным процессом, при этом в связи с использованием явной схемы соседние процессы должны обмениваться крайними значениями, полученными на предыдущем шаге, для выполнения следующего шага.
Программа для решения одномерного уравнения теплопроводности: программа
Видео:Решение уравнения теплопроводности в одномерной постановке в ExcelСкачать

Результаты [ править ]
Найдено решение однородного уравнения теплопроводности в одномерной постановке для 250000 узлов.
| Количество процессов [-] | Время рассчета [сек] |
|---|---|
| 1 | 46.6904 |
| 5 | 11.4576 |
| 10 | 4.79279 |
| 30 | 1.76542 |
| 40 | 1.38313 |
Показано, что при увеличении количества процессов уменьшается время расчета. Также из приведенного графика видно, что для малого числа узлов в сетке использование большого количества процессов не обосновано — выигрыш во времени незначителен.
Видео:Уравнение теплопроводности на полупрямой (решение задачи)Скачать

Научный форум dxdy
Математика, Физика, Computer Science, Machine Learning, LaTeX, Механика и Техника, Химия,
Биология и Медицина, Экономика и Финансовая Математика, Гуманитарные науки
| Вход Регистрация | Donate FAQ Правила Поиск |
Правила форума
В этом разделе нельзя создавать новые темы.
Если Вы хотите задать новый вопрос, то не дописывайте его в существующую тему, а создайте новую в корневом разделе «Помогите решить/разобраться (М)».
Если Вы зададите новый вопрос в существующей теме, то в случае нарушения оформления или других правил форума Ваше сообщение и все ответы на него могут быть удалены без предупреждения.
Не ищите на этом форуме халяву , правила запрещают участникам публиковать готовые решения стандартных учебных задач. Автор вопроса обязан привести свои попытки решения и указать конкретные затруднения.
Обязательно просмотрите тему Правила данного раздела, иначе Ваша тема может быть удалена или перемещена в Карантин, а Вы так и не узнаете, почему.
Видео:8.1 Решение уравнения теплопроводности на отрезкеСкачать

Одномерное уравнение теплопроводности. Численное решение.
Доброго дня суток!
Хотелось бы подробно описать интересующую меня проблему и найти такой же подробный ответ на него. Некоторые вещи мне удалось понять самостоятельно благодаря большому количеству имеющейся в моем запасе литературы:
Теперь, непосредственно само задание(ссылка на скан листа, если что-то не понятно), которое я перепишу в формате
Здесь можно увидеть в самом верху, в рамке находится уравнение теплопроводности:
далее приводится рисунок, отображающий начальное условие системы при t=0:
Заранее оговаривается метод, с помощью которого мы будем численно решать это уравнение:
Сеточные методы на Эйлеровых схемах (явная схема).
Конечно, нужно будет определить устойчивость схемы и выяснить, при каких критических значениях 




Далее приводится 3 уравнения, назначение которых мне не совсем ясно, но имеются догадки:
Видимо, нужно еще варьировать коэффициент 
Суть всего этого задания — реализовать в виде приложения на языке Си/С++, которое показывает зависимость точности решения от шага интегрирования на примере этого самого уравнения теплопроводности , что не составляет труда, если задание понятно и чётко сформулировано. Однако мои текущие познания в области вычислительной математики довольно скудны, поэтому мне довольно проблематично связать текущие соотношения в единую систему.
Во-первых, нужно задать граничные условия для нашего уравнения теплопроводности(исходя из рисунка):
Допустим 

Во-вторых, нужно ввести пространственно-временную сетку, которая будет представлять из себя матрицу, причем каждая строка её[матрицы] характеризует значения уравнения при каком-либо времени 
В-третьих, мы переписываем уравнение теплопроводности в виде разностной схемы: 


В-четвертых, следует учитывать еще эти три уравнения, связанные с самим коэффициентом теплопроводности. Таким образом задача усложняется — требуется понять, каким именно образом следует организовать эту связь и как мы можем вообще их применить либо хотя бы выразить. Я предполагаю, что начальный коэффициент теплопроводности (та самая 
Возникает некоторое количество логичных вопросов:
1. На графике нарисован «стержень» — с равномерной начальной температурой по всей его длине. Что будет означать профиль графика в последующие моменты времени — нагрев окружающей среды и остужение самого стержня?
2. Достаточно ли я описал задачу(для описания её непосредственно в дискретной форме, в ЭВМ) и нет ли где «подводных» камней, либо неопределенности касаемо условий задачи?
3. Каким образом проще и понятнее ввести дополнительные условия для коэффициента теплопроводности(имеются в виду 3 вышеприведенных уравнения)?
4. Мелкие, но необходимые для целостной картины вопросы, описанные выше, в тексте.
5. Правильность моих рассуждений.
Заранее спасибо, если вы смогли осилить этот текст. Просьба: описывайте как можно более подробнее( желательно на пальцах ) свои мысли и объяснения.
В случае успеха я постараюсь выложить понятный алгоритм действий при решении задач такого рода.
Видео:Решение задачи Коши для уравнения теплопроводности (Часть 1)Скачать

Метод Finite Volume — реализация на примере теплопроводности
Метод Finite Volume (FVM)
В основе метода лежит разбиение области на непересекающиеся контрольные объемы(элементы), узловые точки, в которых ищется решение.Узловые точки находятся в центрах контрольных объемов.Также, как и для метода конечных разностей, для каждого элемента составляется уравнение, получается система линейных уравнений.Решая ее — находим значения
искомых переменных в узловых точках.Для отдельного элемента уравнение получается путем интегрирования исходного дифф уравнения по элементу и аппроксимации интегралов.
Термин конечный объем в статье будет часто заменятся на Элемент, будем для удобства считать их эквивалентами (элемент в данной статье не имеет ничего общего с методом конечных элементов).
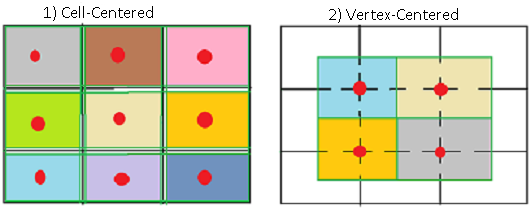
Есть 2 различных способа решения задачи по FVM:
1) грани контрольного объема совпадают с гранями элемента
2) грани контрольного объема проходят через центры граней элементов(на которые разбита область).Искомые переменные хранятся в вершинах этих элементов.Вокруг каждой вершины строится контрольный объем. Для непрямоугольной сетки этот способ имеет еще 2 подвида.
Мы будем использовать способ 1) с контрольными объемами совпадающими с элементами на которые разбита область.
Некоторые плюсы FVM:
- сохранение основных величин по всей области, таких как энергия системы, масса, тепловые потоки и тд.Причом это условие выполняется даже для грубой расчетной сетки
- высокая скорость расчета.Многие расчетные величины можно вычислить при разбиении области на элементы, и вычислять их на каждом шаге по времени нет необходимости.
- легкость использования для задач со сложной геометрией и криволинейными границами.Легкость использования разных геометрических типов элементов — треугольники, полигоны.
Метод FVM реализуем на примере уравнения теплопроводности:
Итак основные шаги при реализации FVM:
- Перевод дифф уравнения в форму пригодную для FVM — интегрирование по контрольному объему
- Составление дискретного аналога, выбор способа перевода производных и других подынтегральных выражений в дискретную форму
- Получение уравнения для каждого из контрольных объемов, на которые разбита область.Составление системы линейных уравнений и ее решение.
Дискретизация по времени.
Немного теории или первый шаг в реализации FVM
FVM на стандартной прямоугольной сетке
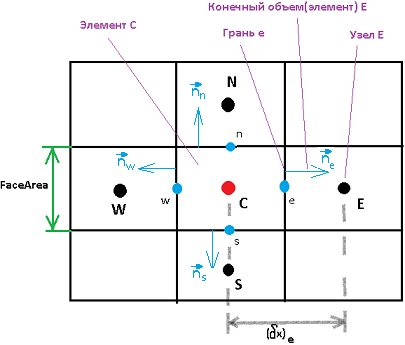
На рисунке изображен Элемент С и его соседние элементы справа(E), слева(W), сверху(N) и снизу(S).У элемента С есть 4 грани обозначенные буквами e w n s.Именно эти 4 грани и составляют периметр элемента и по ним производится интегрирование.Для каждого элемента в результате получаем дискретный аналог исходного дифф уравнения.
Составим дискретный аналог для элемента С.Для начала нужно разобраться с интегралом (3).Интеграл это ведь по факту сумма.Поэтому мы и заменяем интеграл по всей поверхности элемента, на сумму по 4-м составляющим этой поверхности, тоесть 4 граням элемента.
Уравнение (7) и есть конечное уравнение для элемента С, из него мы на каждом шаге по времени получаем новое значение температуры (Tnew) в элементе С.
Граничные условия на прямоугольной сетке
Мы рассмотрим только 2 вида граничных условий.
- Задана температура Tb на границе
- Задан поток FluxB на границе, рассмотрим только случай когда FluxB=0, т.е. грань e будет теплоизолирована(Insulated)
Случай 2) самый простой, поскольку получается что грань e не потребуется при дискретизации(т.к. все коэффициенты Flux=0) и можно ее просто пропустить.
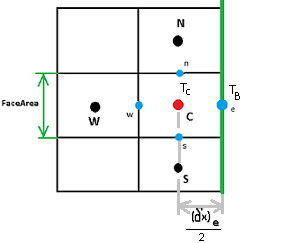
Теперь рассмотрим случай 1).Дискретизация грани e будет в целом похожа на ту что уже была описана.Будут только 2 изменения — вместо Te будет известное граничное значение Tb и вместо расстояния DXe будет DXe/2.В остальном можно рассматривать значение Te так, как будто это был бы обычный соседний узел E.Теперь подробнее распишем терм для граничного элемента С.
Пример численных расчетов на прямоугольной сетке
FVM в задачах со сложной геометрией
Здесь как раз проявляется преимущество FVM, где также, как и в методе конечных элементов, можно представлять область с круглыми границами через разбиение на треугольники или любые другие полигоны.Но FVM имеет еще 1 плюс — при переходе от треугольников к полигонам с большим числом сторон не требуется абсолютно ничего менять, конечно если код был написан для произвольного треугольника а не равностороннего.Более того, можно без изменения кода использовать смесь разных элементов — треугольники, полигоны, квадраты и тд.
Рассмотрим общий случай, когда вектор соединяющий центры 2-х элементов не совпадает с вектором нормали к общей грани этих элементов.Вычисление потока flux через грань теперь будет состоять из 2-х частей.В первой будет расcчитываться ортогональная составляющая а во второй так называемая «кросс-диффузия».
На картинке изображены 2 элемента, С — текущий рассматриваемый элемент и F — соседний элемент.Опишем дискретизацию для грани, разделяющей эти 2 элемента.Вектор соединяющий центры элементов — DCF.Вектор e — это единичный вектор по направлению DCF.Вектор Sf — направлен по нормали к грани, его длинна равна длине грани.
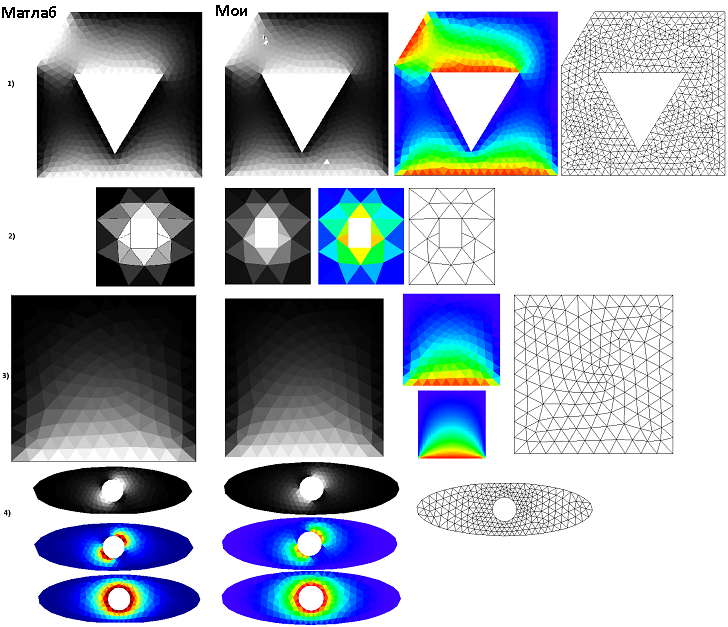
В исходниках я не стал реализовывать терм с кроссдиффузией, т.к встал вопрос — как проверить корректность такой реализации.Визуально сравнение результатов Матлаб и моих ничем не отличалось в отсутствии кросс-диффузии.Видимо это связано с тем что Матлаб любит треугольники близкие к равносторонним, что в итоге делает кроссдиффузию=0.Возможно позже еще вернусь к этому вопросу.
Расчет граничных элементов ничем не отличается от расчетов не на границе, вместо центра соседнего элемента берется центр грани, ну и как обычно подставляется температура на границе.
В моей реализации в итоге получается так:
Примеры и проверка результатов
Описание структуры исходников
Гитхаб с исходниками лежит тут
Основная версия в папке heat2PolyV2.То что относится к вычислительной части лежит в heat2PolyV2SrcFiniteVolume.
Вначале файла Scene2.cs — параметры которые можно менять для отображения в разных цветовых схемах, масштаб, отображение mesh и т.д.Сами примеры хранятся в heat2PolyV2binDebugDemos
Выгрузку из Матлаба сделать просто — нужно открыть pde toolbox, открыть m файл (либо создать самому с нуля), зайти в меню Mesh-Экспорт mesh, нажать ОК; перейти в основной Матлаб, в панельке появятся переменные — матрицы p e t, открыть файл savemymesh.m, выполнить его, появится файл p.out, перенести его в папку Demos.
В исходниках для выбора примера необходимо задать имя файла в строке param.file = «p»;(FormParam.cs).Далее необходимо применить граничные условия — для готовых примеров можно просто раскомментировать соответствующие блоки в MainSolver.cs:
Смысл тут простой — Матлаб разделяет границы по доменам, например внешние и внутренние.Также для каждого домена границы разбиты на части (группы), чтобы можно было задавать условия на участках границы по отдельности — например справа или снизу.
Возможно и вовсе не использовать Матлаб, а вручную прописать все элементы(треугольники) и их вершины + грани(только для граничных элементов)
💡 Видео
Решение Пуассона одномерного уравнения теплопроводностиСкачать

Решение задач теплопроводности (короткая версия)Скачать

Решение первой начально-краевой задачи для одномерного уравнения теплопроводности.Скачать

Вывод уравнения теплопроводностиСкачать

15. Решение уравнения теплопроводности в кругеСкачать

Решение первой краевой задачи для неоднородного уравнения теплопроводности.Скачать

Решение уравнения теплопроводности методом конечных разностейСкачать

12. Как остывает шар (решение уравнения теплопроводности)Скачать

Уравнение в частных производных Уравнение теплопроводностиСкачать

Решение неоднородного уравнения теплопроводностиСкачать

6-1. Уравнение теплопроводностиСкачать

Решение задачи Коши для уравнения теплопроводности (Часть 2)Скачать