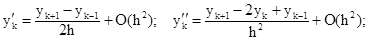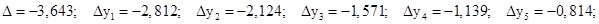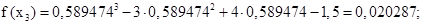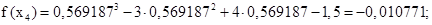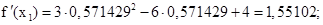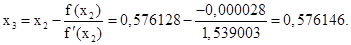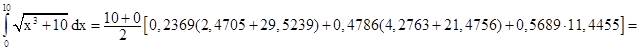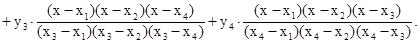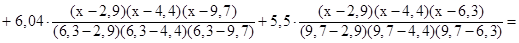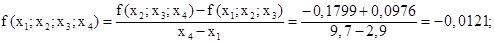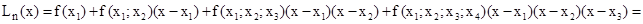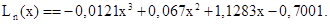Решение обыкновенного дифференциального уравнения второго порядка методом конечных разностей

для обыкновенных дифференциальных уравнений.

Примером краевой задачи является двухточечная краевая задача для обыкновенного дифференциального уравнения второго порядка:

с граничными условиями, заданными на концах отрезка [a; b]:

Следует найти такое решение у(х) на этом отрезке, которое принимает на концах отрезка значения у₀, у₁. Если функция линейна по аргументам , то задача поиска этой функции – линейная краевая задача, в противном случае – нелинейная..

Кроме граничных условий, задаваемых на концах отрезка и называемых граничными условиями первого рода, используются еще условия на производные от решения на концах — граничные условия второго рода:

или линейная комбинация решений и производных – граничные условия третьего рода:

где – такие числа, что

Возможно на разных концах отрезка использовать условия различных типов.

Наиболее распространены два приближенных метода решения краевой задачи:

— метод стрельбы (пристрелки);

Используя конечно-разностный метод, рассмотрим двухточечную краевую задачу для линейного дифференциального уравнения второго порядка на отрезке [а; b].

Введем разностную сетку на отрезке [а; b]:

Решение задачи будем искать в виде сеточной функции:

предполагая, что решение существует и единственно.

Введем разностную аппроксимацию производных следующим образом:

Подставляя эти аппроксимации производных в исходное уравнение, получим систему уравнений для нахождения y_k:

Приводя подобные члены и учитывая, что при задании граничных условий первого рода два неизвестных уже фактически определены, получим систему линейных алгебраических уравнений с трехдиагональной матрицей коэффициентов:

Для этой системы уравнений при достаточно малых шагах сетки h и q(x_k)

Пример. Решить краевую задачу:

с шагом 0,2.

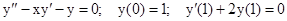
Во всех внутренних узлах отрезка [0; 1] после замены производных их разностными аналогами получим:

На левой границе y₀ = 1, на правой границе аппроксимируем производную односторонней разностью 1-го порядка:

С помощью группировки слагаемых, приведения подобных членов и подстановки значений x_k, а также с учётом у₀ = 1,получим систему линейных алгебраических уравнений:

.

В результате решения системы методом Крамера в Excel, получим:

Решением краевой задачи является табличная функция:

Расчетная часть

3.1. Найти действительные корни уравнения методами простых итераций и касательных (Ньютона) с точностью до 0,00001.

Решение: Для нахождения корня уравнения предварительно отделим корень уравнения графическим методом, записав уравнение в виде:

Построим в осях ХОУ графики функций:

:

Линии графиков пересекаются в единственной точке с абсциссой х₀, лежащей в интервале [0,5; 0,6], т.е.

Значение функции на концах интервала:

Т.к. знаки различны, то уравнение имеет единственный корень в интервале [0,5; 0,6].

3.1.1. Уточнение корня методом простых итераций.

Приведём исходное уравнение к виду:

Т.к. первая производная заданной функции в этом интервале положительна и численно первая производная на этом участке близка к 1,5, то константу С выбираем из интервала:

Т.о. итерационная функция приобретает вид:

Делаем первую итерацию:

Делаем вторую итерацию:

Делаем третью итерацию:

Делаем четвёртую итерацию:

Делаем пятую итерацию:

Делаем шестую итерацию:

Делаем седьмую итерацию:

Делаем восьмую итерацию:

Делаем девятую итерацию:

Продолжая далее, получаем:

На 19-ой итерации изменение шестого знака после запятой, позволяет утверждать, что пятый знак – после запятой – 5. Т.о. значение корня с заданной точностью:

3.1.2. Уточнение корня методом касательных (метод Ньютона):

Т.к. уравнение то же, то интервал, содержащий искомый корень, оставляем тот же [0,5; 0,6], т.е. а = 0,5; b = 0,6.

Находим первую и вторую производную функции :

Очевидно необходимые условия выполняются, т.к.:

, т.е. сохраняют знак на отрезке .

Выполняем первое приближение (х₀ = 0,5):

Выполняем второе приближение (х₁ = 0,571429):

Выполняем третье приближение (х₂ = 0,576128:

Выполняем четвёртое приближение (х₃ = 0,576146):

В пределах заданной точности f(x₂) оказался равен нулю, т.е. требуемая точность достигнута за 4 шага. Значение корня с заданной точностью:

3.2. Вычислить приближенное значение интеграла , используя формулы:

а) трапеций (n = 10); б) Симпсона (n = 10); в) Гаусса (n = 5).

Решение: Ограничимся в расчётах 4 знаками после запятой. Для приближённого вычисления определённого интеграла методом трапеций используется формула:

Разобьём интервал (–1; 9) на n = 10 отрезков (h =1) и вычислим значения подынтегрального выражения для начала и конца каждого отрезка.

№	0	1	2	3	4	5	6	7	8	9	10
х	0	1	2	3	4	5	6	7	8	9	10
	2,4495	2,6458	3,7417	5,7446	8,3666	11,4455	14,8997	18,6815	22,7596	27,1109	31,7175

Тогда по формуле трапеций, имеем:

Используя формулу Симпсона (формулу параболических трапеций) в виде:

получим:

Применяя к исходному интегралу квадратурную формулу Гаусса, имеем:

где

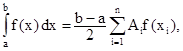
Для n = 5, коэффициенты t_i, представляющие нули полинома Лежандра и коэффициента А_i (эти значения табулированы в справочных таблицах) составляют:

i	1	2	3	4	5
ti	–0,9061	–0,5385	0	0,5385	0,9061
A1	0,2369	0,4786	0,5689	0,4786	0,2369
хi	0,4695	2,3075	5	7,6925	9,5305
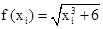	2,4705	4,2763	11,4455	21,4756	29,5239

3.3. Построить интерполяционные многочлены Лагранжа и Ньютона по следующим табличным данным:

	2,9	4,4	6,3	9,7
	2,84	4,53	6,04	5,50

Проверить совпадение значений интерполирующего многочлена с табличными значениями функции в узлах интерполяции.

Решение: Интерполяционный полином Лагранжа для четырёх узлов интерполяции записывается в виде:

Подставим численные значения из заданной таблицы:

Для составления интерполяционного полинома в форме Ньютона, вычислим разности первого порядка для заданной таблицы по формуле:

Вычислим разности второго порядка по формуле:

Вычислим разность третьего порядка по формуле:

Тогда интерполяционный полином Ньютона L_n(x) приобретает следующую форму:

Расчёты показывают, что оба интерполяционных полинома практически одинаковы, т.е. интерполяция ряда точек полиномом третьей степени осуществляется единственным образом.

По заданным узлам интерполяции х_i значения полинома по этому уравнению составляют:

Расчётные значения практически совпадают с заданными значениями f(x).

По полученному уравнению построена кривая, проходящая через узлы интерполяции.

3.4. Найти оценки параметров линейной и квадратичной моделей функциональной зависимости величин у и х по результатам наблюдений , приведенным в таблице:

	0,4	2,4	3,4	4,4	5,4
	2,14	2,14	2,24	2,34	2,34

Построить чертеж: на плоскости нанести экспериментальные точки , построить графики полученных эмпирических функций .

Решение: Коэффициенты «a₀ и а₁» линейной модели найдём, выполнив необходимые вычисления. Расчеты сведем в таблицу:

Номер наблюдения	1	2	3	4	5	Сумма
х	0,4	2,4	3,4	4,4	5,4	16
у	2,14	2,14	2,24	2,34	2,34	11,2
х 2	0,16	5,76	11,56	19,36	29,16	66
х∙y	0,856	5,136	7,616	10,296	12,636	36,54
	2,108	2,202	2,249	2,297	2,344	11,200
	0,0011	0,0039	0,0001	0,0019	0,0000	0,0069

Т.о. линейная зависимость у = а₀ + а₁х имеет вид: у = 2,08865 + 0,0473х.

По этой зависимости определены выровненные значения и остаточная сумма квадратов отклонений, которые записаны в нижних строках таблицы.

Коэффициенты а₀, а₁, а₂ квадратичной зависимости найдём, также выполнив необходимые расчёты в таблице:

Номер наблюдения	1	2	3	4	5	S
х	0,4	2,4	3,4	4,4	5,4	16
у	2,14	2,14	2,24	2,34	2,34	11,2
х 2	0,16	5,76	11,56	19,36	29,16	66
х 3	0,064	13,824	39,304	85,184	157,464	295,84
х 4	0,0256	33,1776	133,634	374,81	850,306	1391,95
у·х	0,856	5,136	7,616	10,296	12,636	36,54
у·х 2	0,3424	12,3264	25,8944	45,3024	68,2344	152,1
	2,128	2,182	2,230	2,292	2,368	11,200
	0,0001	0,0018	0,0001	0,0023	0,0008	0,0051

Составим систему уравнений:

Решение этой системы методом Крамера даёт:

Т.о. квадратичная зависимость у = а₀ + а₁х + а₂х 2 имеет вид:

у = 2,12433 + 0,00729·х + 0,006996·х 2 .

В нижней строке таблицы по полученному уравнению тоже рассчитаны значения по заданным значениям Х и остаточная сумма квадратов отклонений, которые записаны в нижних строках таблицы.

Эмпирическая ломаная, а также линии линейной и квадратичной модели построены на рисунке.

Результаты и выводы.

1. Т.о. интерполяционный полином Лагранжа и Ньютона, построенный по 4 заданным узлам интерполяции имеет вид:

Значения функции, вычисленные по этому полиному третьей степени, точно совпадают с заданными значениями в узлах интерполяции.

Полученное уравнение позволяет найти приближённые значения функции в любых промежуточных точках от х₁ = 2,9 до х₄ = 9,7.

2. Применение метода минимальных квадратов (МНК) к аппроксимации пяти экспериментальных точек линейной зависимостью вида у = а₀ + а₁х, т.е. прямой линией и квадратичной зависимостью вида 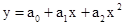, т.е. параболой дало следующие выражения:

– линейная зависимость реализована уравнением: у = 2,0887 + 0,0473х

– квадратичная зависимость реализована уравнением: у = 2,1243 + 0,0073·х + 0,007·х 2 .

Судя по остаточной сумме квадратов отклонений, квадратичная зависимость несколько лучше аппроксимирует экспериментальные данные, т.к. для неё остаточная сумма квадратов отклонений меньше, чем для линейной функции.

Список использованной литературы

1. Самарский А.А. Гулин А.В. Численные методы. М. МГУ. 1989 год.

2. Н. С. Бахвалов; Н.П. Жидков; Г.М. Кобельков. Численные методы. М 2003 год;

3. В.А. Буслов, С.Л.Яковлев. Численные методы и исследование функций. СПГУ. Курс лекций. СПБ 2001 г

4. Г.А. Зуева. Метод наименьших квадратов и его применение. Электронное учебное пособие. Иваново, 2009

Видео:Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентамиСкачать

Краевые задачи для дифференциальных уравнений второго порядка

Пример 1. Рассмотрим простейшую двухточечную краевую задачу.

Найти функцию , удовлетворяющую дифференциальному уравнению второго порядка вида:

и принимающую при и заданные значения . Геометрически (Рис.10) это означает, что требуется найти интегральную кривую, проходящую через данные точки и .

Пример 2. Найти такое решение дифференциального уравнения (40), чтобы производные имели заданное значение . Геометрически (Рис.11) это сводится к отысканию интегральной кривой, пересекающей прямые и под заданными соответственно углами и такими, что и .

Видео:16. Линейные неоднородные дифференциальные уравнения 2-го порядка с постоянными коэффициентамиСкачать

Решение краевой задачи для обыкновенного дифференциального уравнения второго порядка методом конечных разностей

Рассмотрим двухточечную краевую задачу для линейного дифференциального уравнения. Найти решение уравнения

с дополнительными краевыми условиями

где числа считаются известными и

то есть одна из величин не равна нулю.

Коэффициенты являются непрерывными функциями на некотором отрезке . Решением этого уравнения является некоторая непрерывная на функция , имеющая первую и вторую производные на , удовлетворяющая исходному уравнению и дополнительным краевым условиям.

Поставленная краевая задача решается с помощью перехода от исходной задачи к новой, записанной в конечно-разностной форме. Тогда решение новой задачи будет являться приближенным решением исходной задачи. В силу того, что первая и вторая производные, входящие в уравнение и в краевые условия, будут заменены приближенными конечно-разностными формулами, решения с применением метода конечных разностей получается не в виде непрерывной функции , а виде таблицы ее значений в отдельных точках (Рис.12). Для этого разобьем на частей так, чтобы . Наша задача — найти значения функции в точках . Для того, чтобы перейти от исходной задачи к конечно-разностной, надо получить формулы для представления первой и второй производных в конечно-разностном виде. Они получаются, если применить разложение функции в окрестности некоторой точки в ряд Тейлора, ограничиваясь вторыми производными:

Складываем эти ряды и получаем выражение второй производной в конечно-разностной форме:

Аналогично получим формулу для первой производной, если вычтем ряды:

С учетом введенных обозначений запишем исходное уравнение для узловых точек :

в конечно-разностной форме, тогда к системе (43) добавляется еще два уравнения, соответствующие краевым условиям:

Получили систему линейных алгебраических уравнений (43) — (45) с неизвестными . Решив эту систему любым известным методом, получим приближенное решение для исходной задачи.

Заметим, что система представляет собой систему с разряженной матрицей, имеющей трехдиагональный вид. Поэтому, для решения системы применяют специальные методы, позволяющие оперировать только с элементами матрицы, отличными от нуля. Одним из таких методов является метод прогонки.

🎬 Видео

6-2. Метод сетокСкачать

Операционное исчисление. Решить неоднородное дифференциальное уравнение 2 порядкаСкачать

Линейное неоднородное дифференциальное уравнение с постоянными коэффициентами 4y''-y=x^3-24x #1Скачать

Линейное однородное дифференциальное уравнение 2-го порядка с постоянными коэффициентами.Скачать

Задача Коши ➜ Частное решение линейного однородного дифференциального уравненияСкачать

Линейное дифференциальное уравнение Коши-ЭйлераСкачать

14. Дифференциальные уравнения второго порядка, допускающие понижение порядкаСкачать

19. Метод вариации произвольных постоянных. Линейные неоднородные диф уравнения 2-го порядкаСкачать

15. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентамиСкачать

ЛОДУ 2 порядка c постоянными коэффициентамиСкачать

Линейное неоднородное дифференциальное уравнение 2 способаСкачать

Решение уравнения теплопроводности методом конечных разностейСкачать

18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать

Неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентами МЕТОДОМ ЛАПЛАСАСкачать

13. Операционное исчисление. Решить неоднородное ДУ 2 порядкаСкачать

Метод ЭйлераСкачать

2. Метод разделения операторов. Метод конечных разностейСкачать