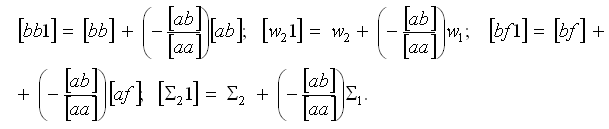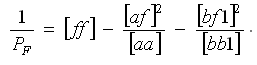Решение нормальных уравнений методом гаусса геодезия

Видео:Решение системы уравнений методом Гаусса 4x4Скачать

Решение нормальных уравнений по алгоритму Гаусса

Решение нормальных уравнений выполняют в схеме Гаусса (табл. 2).

Для вычисления преобразованных коэффициентов нужно постоянный множитель (-[ab]/[aa]), стоящий в первой элиминационной строке над квадратичным коэффициентом [bb], умножать по строке на вышестоящие числа и складывать каждый раз с элементами второго нормального уравнения

Схема решения нормальных уравнений коррелат (r = 2; π_i = 1)

Правило развертывания символа Гаусса: «Cимвол развертывается в разность. Уменьшаемое — тот же символ, но со значком на единицу меньше. Вычитаемое — дробь. Знаменатель дроби — квадратичный коэффициент, буква которого соответствует номеру развертываемого символа. Числитель — произведение двух символов, каждый из которых получен заменой буквы уменьшаемого на букву знаменателя».

Последняя коррелата равна числу, стоящему в столбце w последней элиминационной строки. Коррелата к₁ вычисляется с использованием чисел первой элиминационной строки от столбца w налево.

[vv] или [pvv] — для неравноточных измерений — получают как сумму произведений чисел элиминационных строк столбца w на вышестоящие числа того же столбца, знак «минус» отбрасывают:

(16)

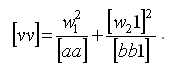
Обратный вес функции 1/P_F получают, как сумму [ff] и произведений чисел элиминационных строк столбца F на вышестоящие числа того же столбца:

Заключительный контроль решения нормальных уравнений осуществляется подстановкой коррелат в суммарное уравнение:

Видео:Математика без Ху!ни. Метод Гаусса.Скачать

Лекции по дисциплине Геодезия (стр. 3 )

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7

Такая наука, как геодезия тесно связана с измерениями, которые сопровождаются неизбежными ошибками. Если обозначим:

У – истинное значение измеряемой величины;

у – результат измерений;

— истинная ошибка.

то истинная ошибка может быть вычислена по формуле:

(15)

2 Виды ошибок измерений

По источникам и характеру ошибки делятся на грубые, систематические и случайные.

Грубые ошибки являются, как правило, следствие промахов, просчетов в измерениях, неисправностями инструментов и приборов, резким ухудшением внешних условий и пр. Они обнаруживаются при несоблюдении допусков и контролей и исключаются повторными измерениями.

Систематические – те, которые знаком или величиной однообразно повторяются в многократных измерениях. Их источниками являются неисправности в применяемых инструментах, неточная установка инструментов, личные физиологические особенности наблюдателя, влияние внешних факторов и т. п.

Примеры систематических ошибок:

— ошибка в измеренном значении длины линии на местности из-за отклонения мерной ленты от створа;

— ошибка в определении длины мерного прибора (ошибка компарирования).Эта ошибка постоянна и действует пропорционально измеренному расстоянию;

— систематическая ошибка нанесения шрихов лимба теодолита.

Влияние систематических ошибок сводят к допустимому минимуму путем тщательной поверки инструментов, применения соответствующей методики измерений, а также путем введения поправок в результаты измерений.

Некоторые рекомендации по уменьшению влияния систематических ошибок измерения:

— устанавливают закон появления систематической ошибки, после чего ошибку устраняют введением поправки в результаты измерений. Например, эталонирование мерного прибора и введение потом поправок за длину и температуру;

— применяют соответствующую методику измерений, чтобы систематические ошибки меняли знак. Например:

1) отсчитывание по диаметрально противоположным штрихам лимба, что приводит к исключению влияния эксцентриситета алидады;

2) перестановка лимба между приёмами на угол 180˚/n, где n-число приёмов ( при этом ослабевает влияние систематических ошибок штрихов лимба);

— используют определённую методику обработки результатов измерений. Например, углы и координаты вытянутого теодолитного хода уравнивают раздельно. Это ведёт к ослаблению влияния систематических ошибок угловых и линейных измерений.

Таким образом, будем считать, что результаты измерений содержат только слуайные ошибки, т. е. такие, размер и характер влияния которых на каждый отдельный результат измерения остается неизвестным.

3 Свойства случайных ошибок

Величину и знак случайных погрешностей установить нельзя.

Примеры случайных ошибок:

— ошибки отсчитывания по угломерному кругу;

— часть ошибки визирования, обусловленную колебаниями изображения;

— случайные ошибки нанесения штрихов лимба;

— влияние вибрации сигнала;

— ошибка отсчитывания по нивелирной рейке;

— ошибка за округление чисел при вычислениях.

Если результаты измерений содержат только случайные ошибки (грубые и систематические исключают), то

Чем ближе результат измерений к истинному значению, тем он точнее. Чем меньше ошибки, тем выше точность.

4 Обработка рядя равноточных измерений.

По точности результаты измерений разделяют на равноточные и неравноточные.

Под равноточными понимают однородные результаты, полученные при измерениях одним и тем же инструментом, одинаковым числом приемов, одним и тем же или равноценными методами и в одинаковых условиях.

5 Критерии оценки точности результатов измерений.

В геодезии необходиом уметь оценивать точность результатов измерений. Основным критерием точности в геодезии является средняя квадратическая ошибка (СКО). Ее математическое выражение:

, (16)

то есть квадрат СКО равен математическому ожиданию квадрата истинной ошибки.

Для оценки точности отдельного измерения применяется формула Гаусса:

или (17)

— случайная ошибка, тоже истинная, но

θ- истинная ошибка в более широком смысле. Она может состоять из случайной и систематической частей.

СПРАВКА: (1777 – 1855гг) – немецкий математик. Автор работ по астрономии. геодезии. физике. Разработал математические основы высшей геодезии, вычисляя погрешности при измерениях, разработал метод наименьших квадратов.

Кроме основной характеристики m, характеризующей влияние случайных ошибок на результаты измерений. иногда применяют дополнительную характеристику – среднюю ошибку

,

но СКО имеет ряд преимуществ по сравнению со средней квадратической погрешностью:

— на величину СКО сильнее влияют большие по абсолютной величине ошибки;

— СКО – устойчивая характеристика, даже при небольшом числе измерений даёт надёжные результаты.

Если — среднее арифметическое или арифметическая средина, то СКО арифметической средины М находится по формуле

где n – число измерений;

m – СКО одного измерения.

Для решения практических задач используется предельная ошибка ∆пред. Для серии ошибок в качестве ∆пред принимается утроенная СКО.

Это допуск, предел, больше которого не должно быть ошибки.

На практике во многих работах для повышения требований к точности измерений за предельную ошибку принимают удвоенную СКО.

Все приведённые выше ошибки называются абсолютными ошибками. Кроме абсолютных бывают относительные ошибки fотн, которыми называют отношение абсолютной ошибки к среднему значению измеряемой величины. Относительная ошибка выражается дробью, числитель которой равен 1, а знаменатель – отношение среднего значения измеряемой величины к абсолютной ошибке.

Приведенная выше формула Гаусса 17 применима для случаев, когда известны истинные значения измеряемых величин (или истинные ошибки). Эти случаи в практике редки. Известны они могут быть например, при моделировании, или за истинные значения принимают результаты измерений более высокой точности.

6 Арифметическая средина и ее средняя квадратичная ошибка

Как правило, истинные значения измеряемых величин неизвестны, но из измерений можно получить наиболее надежный результат – арифметическую средину по формуле:

(18)

=

Вычислив уклонение отдельных измерений от арифметической средины

, (19)

можно СКО одного измерения определить по формуле Бесселя:

(20)

Справка: (1784 – 1846гг) – немецкий астроном. член Берлинской АН. Он один из первых определил расстояние до звёзд. Реформировал методы учёта инструментальных и других ошибок, что повысило точность астрономических измерений.

7Средние квадратичные ошибки функций измеренных величин.

Формулы Гаусса и Бесселя определяют СКО непосредственно измеренных величин. Если определяемая величина является функцией других непосредственно измеряемых величин, то СКО функции может быть найдена по формуле:

где — СКО функции;

— функция многих независимых аргументов ;

— частные производные от функции по каждой переменной (результату измерений);

— СКО каждого результата измерений.

8 Неравноточные измерения.

9 Понятие о весе.

На практике часто производятся неравноточные измерения, которые выполнены в различных условиях, приборами различной точности, различным числом приемов и т. д. В этом случае уже нельзя ограничиваться простым арифметическим средним, а необходимо учитывать степень надежности каждого результата измерений. Надежность результата, выраженная числом, называется его весом. Чем надежнее результат, тем больше его вес. Следовательно, вес связан с точностью результата измерения, которая характеризуется СКО. Поэтому вес результата измерения принимают обратно пропорциональным квадрату СКО, то есть:

, (22)

где — некоторая постоянная величина, коэффициент пропорциональности;

— СКО измерения.

Таким образом, вес – относительная характеристика точности измерений. Использование веса вместо СКО облегчает. упрощает формулы математической обработки в случае неравноточных измерений. Необходим вес и потому, что более точные измерения в большей степени должны влиять на окончательный результат. (Для облегчения задачи отыскивания весов обычно вес какого-либо результата принимают за единицу и относительно его вычисляют веса остальных неизвестных.)

Если вес результат какого-либо измерения принять равным единице, а СКО измерения его обозначить через , то общее выражение веса примет вид:

, (23)

где — ср. кв. ош-ка единицы веса.

В практике геодезических работ в качестве весов принимают:

— при обработке результатов угловых измерений одним и тем же прибором – величины, пропорциональные количеству измерений каждого угла; для суммы углов в ходе, имеющем ni вершин,

— при обработке линейных измерений одним и тем же мерным прибором вес вычисляется по формуле

где si – длина линии;

— при обработке превышений из геометрического нивелирования — величины, обратно пропорциональные длине ходов или числу станций;

— при тригонометрическом нивелировании вес вычисляется по формуле

где si – расстояние между пунктами.

Принципы уравнивания геодезических сетей

1 Уравнивание геодезических сетей по МНК коррелатным способом.

2 Средняя квадратичная ошибка единицы веса

Геодезические измерения характерны тем, что их всегда больше, чем необходимо для определения искомых величин. Необходимыми называют такие измерения, которые позволяют однократно, бесконтрольно найти определяемые величины. Избыточными измерениями называются те, которые выполняют сверх необходимых. Например, для решения треугольника измеряют три угла, тогда как было бы достаточно измерить два угла.

Избыточные измерения позволяют:

— проконтролировать результаты измерений;

— в среднем повысит точность определяемых величин;

— выполнить оценку точности этих величин.

Число избыточных измерений определяется по формуле , (24)

где — число всех измерений в сети;

— число необходимых измерений.

Геодезические измерения ведутся в создаваемых на местности геодезических построениях, истинные элементы которых, в том числе и измеряемые, связаны между собой Математическими зависимостями.

Каждое избыточное измерение приводит к появлению математического соотношения с другими измеренными величинами. Неизбежные ошибки в измерениях приводят к появлению невязок в этих соотношениях. Для устранения невязок необходимо уравнивание результатов измерений.

Уравнивание – это математическая обработка результатов измерений, позволяющая:

— найти наиболее надежные (вероятнейшие) значения неизвестных с оценкой точности полученных результатов;

— исключить все математические противоречия в зависимостях, существующих между измеряемыми величинами.

ВЫВОД: сама задача уравнивания может быть поставлена только при наличии в сети избыточных измерений.

Целью уравнивания является:

— нахождение таких поправок к результатам измерений, которые не только компенсировали бы невязки, но и наилучшим образом приблизили уравненные значения измеренных величин к их истинным значениям;

— повышение точности всех измеренных величин;

— выполнение оценки точности по материалам уравнивания.

Может быть найдено множество систем поправок (множество вариантов), ликвидирующих невязки, но только одна система поправок позволяет найти вероятнейшие (т. е. наиболее приближённые к истинным) значения определяемых величин (и их функций).

Такая система поправок находится под условиями 25 и 26:

— для равноточных измерений,

(условие Лежандра) (25)

-для неравноточных измерений)

(условие Гаусса) (26)

Первое условие – сумма квадратов поправок в непосредственные измерения должна быть минимальной.

Второе условие – сумма произведений квадратов поправок на веса соответствующих результатов измерений должна быть минимальной.

Уравнивание под условиями 25 и 26 называют уравниванием по методу наименьших квадратов (МНК), а условия (25) и (26) – принципом наименьших квадратов.

Уравнивание по МНК – строгое. Другие способы нахождения поправок – приближённое уравнивание.

Для решения задачи уравнивания по МНК применяются два основных способа:

— коррелатный, основанный на способе Лагранжа с неопределенными множителями для нахождения условного экстремума;

— параметрический – способ абсолютного экстремума, при котором все измеренные величины представляют в виде функций некоторых независимых неизвестных параметров.

Существуют также комбинированные способы уравнивания – коррелатный с дополнительными неизвестными и параметрический с избыточными параметрами.

1 Уравнивание геодезических сетей по МНК коррелатным способом

Пусть выполнено измерений их которых — необходимых.

— результаты измерений;

— истинные значения измеренных величин;

— установленная система весов результатов измерений;

— обратные веса.

Связь между ними может быть выражена следующими соотношениями:

, (27)

где

— случайные ошибки;

. (28)

Число избыточных измерений , где .

Каждое избыточное измерение приводит к математическому соотношению между истинными значениями измеренных величин, т. е. в геодезической сети возникает условий:

, (29)

где

( т. е. здесь r функций: ).

Эта исходная система условных уравнений связи включает только независимые уравнения, число которых равно

Вследствие неизбежных ошибок в измерениях, эти же функции, но от измеренных величин примут вид:

где — невязки.

Это выражение называется системой условных уравнений связи от измеренных значений.

(31)

Отдельные ошибки неизвестны, но их совокупность (сумма) в каждом условии может быть вычислена.

Необходимо найти такие поправки к результатам измерений, которые ликвидируют невязки, то есть должно выполняться равенство:

, (32)

где поправки к результатам измерений;

Уравненные результаты измерений находят по формуле:

(33)

Тогда система условных уравнений связи от уравненных значений примет вид:

(34)

где

В правой части опять нули, т. к. невязки компенсировались поправками.

Систему (34) приводят к линейному виду, раскладывая каждое уравнение в ряд Тейлора, и пренебрегая при этом малыми (нелинейными) членами разложения:

Первое слагаемое согласно формуле (30) является невязкой , поэтому выражение (35) примет вид:

Обозначим частные производные от первой функции буквой , от второй —, от третьей —и т. д. То есть:

, ,…,;

, ,…, (37)

, ,…,

С учетом (37) система (36) примет вид:

(38)

Это система условных уравнений поправок. В ней:

— невязки;

— коэффициенты при поправках;

— неизвестные поправки, которые надо найти, решив систему (38).

Так как в системе (38) число уравнений меньше числа неизвестных поправок , то такая система имеет множество решений, т. е. не решается однозначно. Чтобы из множества вариантов выбрать один, наилучший, необходимо поставить дополнительное условие. Это условие:

(39)

является принципом наименьших квадратов.

Вывод нормальных уравнений коррелат представляется в матричной форме. Система (38) условных уравнений поправок

решается под условием (39) МНК

,

где — матрица коэффициентов при поправках условных уравнений поправок;

— вектор поправок;

— трансформированный вектор поправок;

— вектор свободных членов;

— матрица весов результатов измерений;

Используя метод Лагранжа с неопределенными множителями, называемыми в геодезии коррелатами, представленными в виде вектора коррелат (40)

составляют функцию Лагранжа (41)

чтобы найти min, находят производную от этой функции (42)

, (43)

(44)

где — трансформированная матрица коэффициентов при поправках;

— вектор коррелат.

Полагая, что , как симметричная матрица, получим коррелатное уравнение поправок, выражающее поправки в виде функций коррелат

(45)

— матрица обратных весов результатов измерений;

— обратный вес результата измерений;

— единичная матрица – т. е. уравнение (45) можно представить в виде

(46)

Выражение (46) является коррелатным уравнением поправок.

Подставив (46) в (38), получают систему нормальных уравнений коррелат:

(47)

,

где — матрица коэффициентов нормальных уравнений.

Коэффициенты, стоящие на главной диагонали, называются квадратичными, они всегда положительны, остальные – неквадратичные.

(48)

В системе нормальных уравнений коррелат (48) — неизвестные коррелаты. Их число r, как и число уравнений, поэтому система (48) решается однозначно.

Способы решения могут быть различны:

— по схеме Гаусса;

— методом исключения, когда из последнего уравнения выражается последнее неизвестное, подставляется в предыдущее уравнение и т. д.;

— на ЭВМ, по готовым программам.

Из решения нормальных уравнений находят коррелаты , а по ним поправки:

(49)

Выражение (49) называется коррелатным уравнением поправок.

Контролем вычисления поправок является равенство:

(50)

После этого вычисляют уравненные значения результатов измерений

, () (51)

и делают контроль уравнивания путем подстановки уравненных измерений в условные уравнения связи

(52)

2 Средняя квадратическая ошибка единицы веса

Оценка точности по результатам уравнивания, то есть по поправкам, может быть выполнена по формуле:

, (53)

где — средняя квадратическая ошибка единицы веса, то есть ошибка измерения с весом .

Чтобы оценить какой-либо элемент сети (отметку, координату, угол и т. д.) необходимо составить функцию, то есть математически выразить этот элемент.

(54)

где — средняя квадратическая ошибка функции;

— вес функции.

1 Уравнивание одиночного нивелирного хода коррелатным способом

Рассмотрим нивелирный ход

Рисунок 9 — Нивелирный ход

— исходные пункты;

— отметки исходных пунктов;

— измеренные превышения;

— длины секций;

— определяемые пункты, отметки которых необходимо найти.

Уравнивание нивелирного хода начинается с подсчета числа избыточных измерений по формуле

(55)

В ходе, представленном на рисунке 9, число измеренных превышений . Число необходимых измерений — по числу определяемых пунктов. Поэтому .

Контроль вычисления производится по формуле , (56)

где — число замкнутых полигонов;

— число исходных пунктов.

Таким образом, в нивелирном ходе возникает только одно условие и соответственно одно условное уравнение связи:

(57)

где — невязка.

Так как , то, согласно общей теории уравнивания, составляется одно нормальное уравнение коррелат

, (58)

где — обратные веса;

при , обратные веса ;

— коэффициенты при поправках условного уравнения поправок

(59)

Коэффициенты находятся как частные производные от функции по результатам измерений , т. е. , ,…, .

Видео:Решение системы уравнений методом ГауссаСкачать

Метода Гаусса: примеры решения СЛАУ

В данной статье мы:

• дадим определение методу Гаусса,
• разберем алгоритм действий при решении линейных уравнений, где количество уравнений совпадает c количеством неизвестных переменных, а определитель не равен нулю;
• разберем алгоритм действий при решении СЛАУ с прямоугольной или вырожденной матрицей.

Видео:Система линейных уравнений. Общее решение. Метод ГауссаСкачать

Метод Гаусса — что это такое?

Метод Гаусса — это метод, который применяется при решении систем линейных алгебраических уравнений и имеет следующие преимущества:

• отсутствует необходимость проверять систему уравнений на совместность;
• есть возможность решать системы уравнений, где:
• количество определителей совпадает с количеством неизвестных переменных;
• количество определителей не совпадает с количеством неизвестных переменных;
• определитель равен нулю.
• результат выдается при сравнительно небольшом количестве вычислительных операций.

Видео:Метод Гаусса решения систем линейных уравненийСкачать

Основные определения и обозначения

Есть система из р линейных уравнений с n неизвестными ( p может быть равно n ):

a 11 x 1 + a 12 x 2 + . . . + a 1 n x n = b 1 a 21 x 1 + a 22 x 2 + . . . + a 2 n x n = b 2 ⋯ a p 1 x 1 + a p 2 x 2 + . . . + a p n x n = b p ,

где x 1 , x 2 , . . . . , x n — неизвестные переменные, a i j , i = 1 , 2 . . . , p , j = 1 , 2 . . . , n — числа (действительные или комплексные), b 1 , b 2 , . . . , b n — свободные члены.

Если b 1 = b 2 = . . . = b n = 0 , то такую систему линейных уравнений называют однородной, если наоборот — неоднородной.

Решение СЛАУ — совокупность значения неизвестных переменных x 1 = a 1 , x 2 = a 2 , . . . , x n = a n , при которых все уравнения системы становятся тождественными друг другу.

Совместная СЛАУ — система, для которой существует хотя бы один вариант решения. В противном случае она называется несовместной.

Определенная СЛАУ — это такая система, которая имеет единственное решение. В случае, если решений больше одного, то такая система будет называться неопределенной.

Координатный вид записи:

a 11 x 1 + a 12 x 2 + . . . + a 1 n x n = b 1 a 21 x 1 + a 22 x 2 + . . . + a 2 n x n = b 2 ⋯ a p 1 x 1 + a p 2 x 2 + . . . + a p n x n = b p

Матричный вид записи: A X = B , где

A = a 11 a 12 ⋯ a 1 n a 21 a 22 ⋯ a 2 n ⋯ ⋯ ⋯ ⋯ a p 1 a p 2 ⋯ a p n — основная матрица СЛАУ;

X = x 1 x 2 ⋮ x n — матрица-столбец неизвестных переменных;

B = b 1 b 2 ⋮ b n — матрица свободных членов.

Расширенная матрица — матрица, которая получается при добавлении в качестве ( n + 1 ) столбца матрицу-столбец свободных членов и имеет обозначение Т .

T = a 11 a 12 ⋮ a 1 n b 1 a 21 a 22 ⋮ a 2 n b 2 ⋮ ⋮ ⋮ ⋮ ⋮ a p 1 a p 2 ⋮ a p n b n

Вырожденная квадратная матрица А — матрица, определитель которой равняется нулю. Если определитель не равен нулю, то такая матрица, а потом называется невырожденной.

Видео:Метод Гаусса и метод Жордана-Гаусса ➜ 2 метода за 7 минутСкачать

Описание алгоритма использования метода Гаусса для решения СЛАУ с равным количеством уравнений и неизвестных (обратный и прямой ход метода Гаусса)

Для начала разберемся с определениями прямого и обратного ходов метода Гаусса.

Прямой ход Гаусса — процесс последовательного исключения неизвестных.

Обратный ход Гаусса — процесс последовательного нахождения неизвестных от последнего уравнения к первому.

Алгоритм метода Гаусса:

Решаем систему из n линейных уравнений с n неизвестными переменными:

a 11 x 1 + a 12 x 2 + a 13 x 3 + . . . + a 1 n x n = b 1 a 21 x 1 + a 22 x 2 + a 23 x 3 + . . . + a 2 n x n = b 2 a 31 x 1 + a 32 x 2 + a 33 x 3 + . . . + a 3 n x n = b 3 ⋯ a n 1 x 1 + a n 2 x 2 + a n 3 x 3 + . . . + a n n x n = b n

Определитель матрицы не равен нулю.

1. a 11 не равен нулю — всегда можно добиться этого перестановкой уравнений системы;
2. исключаем переменную x 1 из всех уравнений систему, начиная со второго;
3. прибавим ко второму уравнению системы первое, которое умножено на — a 21 a 11 , прибавим к третьему уравнению первое умноженное на — a 21 a 11 и т.д.

После проведенных действий матрица примет вид:

a 11 x 1 + a 12 x 2 + a 13 x 3 + . . . + a 1 n x n = b 1 a ( 1 ) 22 x 2 + a ( 1 ) 23 x 3 + . . . + a ( 1 ) 2 n x n = b ( 1 ) 2 a ( 1 ) 32 x 2 + a ( 1 ) 33 x 3 + . . . + a ( 1 ) 3 n x n = b ( 1 ) 3 ⋯ a ( 1 ) n 2 x 2 + a ( 1 ) n 3 x 3 + . . . + a ( 1 ) n n x n = b ( 1 ) n ,

где a i j ( 1 ) = a i j + a 1 j ( — a i 1 a 11 ) , i = 2 , 3 , . . . , n , j = 2 , 3 , . . . , n , b i ( 1 ) = b i + b 1 ( — a i 1 a 11 ) , i = 2 , 3 , . . . , n .

Далее производим аналогичные действия с выделенной частью системы:

a 11 x 1 + a 12 x 2 + a 13 x 3 + . . . + a 1 n x n = b 1 a ( 1 ) 22 x 2 + a ( 1 ) 23 x 3 + . . . + a ( 1 ) 2 n x n = b ( 1 ) 2 a ( 1 ) 32 x 2 + a ( 1 ) 33 x 3 + . . . + a ( 1 ) 3 n x n = b ( 1 ) 3 ⋯ a ( 1 ) n 2 x 2 + a ( 1 ) n 3 x 3 + . . . + a ( 1 ) n n x n = b ( 1 ) n

Считается, что a 22 ( 1 ) не равна нулю. Таким образом, приступаем к исключению неизвестной переменной x 2 из всех уравнений, начиная с третьего:

• к третьему уравнению систему прибавляем второе, которое умножено на — a ( 1 ) 42 a ( 1 ) 22 ;
• к четвертому прибавляем второе, которое умножено на — a ( 1 ) 42 a ( 1 ) 22 и т.д.

После таких манипуляций СЛАУ имеет следующий вид:

a 11 x 1 + a 12 x 2 + a 13 x 3 + . . . + a 1 n x n = b 1 a ( 1 ) 22 x 2 + a ( 1 ) 23 x 3 + . . . + a ( 1 ) 2 n x n = b ( 1 ) 2 a ( 2 ) 33 x 3 + . . . + a ( 2 ) 3 n x n = b ( 2 ) 3 ⋯ a ( 2 ) n 3 x 3 + . . . + a ( 2 ) n n x n = b ( 2 ) n ,

где a i j ( 2 ) = a ( 1 ) i j + a 2 j ( — a ( 1 ) i 2 a ( 1 ) 22 ) , i = 3 , 4 , . . . , n , j = 3 , 4 , . . . , n , b i ( 2 ) = b ( 1 ) i + b ( 1 ) 2 ( — a ( 1 ) i 2 a ( 1 ) 22 ) , i = 3 , 4 , . . . , n . .

Таким образом, переменная x 2 исключена из всех уравнений, начиная с третьего.

Далее приступаем к исключению неизвестной x 3 , действуя по аналоги с предыдущим образцом:

a 11 x 1 + a 12 x 2 + a 13 x 3 + . . . + a 1 n x n = b 1 a ( 1 ) 22 x 2 + a ( 1 ) 23 x 3 + . . . + a ( 1 ) 2 n x n = b ( 1 ) 2 a ( 2 ) 33 x 3 + . . . + a ( 2 ) 3 n x n = b ( 2 ) 3 ⋯ a ( n — 1 ) n n x n = b ( n — 1 ) n

После того как система приняла такой вид, можно начать обратный ход метода Гаусса:

• вычисляем x n из последнего уравнения как x n = b n ( n — 1 ) a n n ( n — 1 ) ;
• с помощью полученного x n находим x n — 1 из предпоследнего уравнения и т.д., находим x 1 из первого уравнения.

Найти решение системы уравнений методом Гаусса:

3 x 1 + 2 x 2 + x 3 + x 4 = — 2 x 1 — x 2 + 4 x 3 — x 4 = — 1 — 2 x 1 — 2 x 2 — 3 x 3 + x 4 = 9 x 1 + 5 x 2 — x 3 + 2 x 4 = 4

Коэффициент a 11 отличен от нуля, поэтому приступаем к прямому ходу решения, т.е. к исключению переменной x 11 из всех уравнений системы, кроме первого. Для того, чтобы это сделать, прибавляем к левой и правой частям 2-го, 3-го и 4-го уравнений левую и правую часть первого, которая умножена на — a 21 a 11 :

— 1 3 , — а 31 а 11 = — — 2 3 = 2 3 и — а 41 а 11 = — 1 3 .

3 x 1 + 2 x 2 + x 3 + x 4 = — 2 x 1 — x 2 + 4 x 3 — x 4 = — 1 — 2 x 1 — 2 x 2 — 3 x 3 + x 4 = 9 x 1 + 5 x 2 — x 3 + 2 x 4 = 4 ⇔

⇔ 3 x 1 + 2 x 2 + x 3 + x 4 = — 2 x 1 — x 2 + 4 x 3 — x 4 + ( — 1 3 ) ( 3 x 1 + 2 x 2 + x 3 + x 4 ) = — 1 + ( — 1 3 ) ( — 2 ) — 2 x 1 — 2 x 2 — 3 x 3 + x 4 + 2 3 ( 3 x 1 + 2 x 2 + x 3 + x 4 ) = 9 + 2 3 ( — 2 ) x 1 + 5 x 2 — x 3 + 2 x 4 + ( — 1 3 ) ( 3 x 1 + 2 x 2 + x 3 + x 4 ) = 4 + ( — 1 3 ) ( — 2 ) ⇔

⇔ 3 x 1 + 2 x 2 + x 3 + x 4 = — 2 — 5 3 x 2 + 11 3 x 3 — 4 3 x 4 = — 1 3 — 2 3 x 2 — 7 3 x 3 + 5 3 x 4 = 23 3 13 3 x 2 — 4 3 x 3 + 5 3 x 4 = 14 3

Мы исключили неизвестную переменную x 1 , теперь приступаем к исключению переменной x 2 :

— a 32 ( 1 ) a 22 ( 1 ) = — — 2 3 — 5 3 = — 2 5 и а 42 ( 1 ) а 22 ( 1 ) = — 13 3 — 5 3 = 13 5 :

3 x 1 + 2 x 2 + x 3 + x 4 = — 2 — 5 3 x 2 + 11 3 x 3 — 4 3 x 4 = — 1 3 — 2 3 x 2 — 7 3 x 3 + 5 3 x 4 = 23 3 13 3 x 2 — 4 3 x 3 + 5 3 x 4 = 14 3 ⇔

⇔ 3 x 1 + 2 x 2 + x 3 + x 4 = — 2 — 5 3 x 2 + 11 3 x 3 — 4 3 x 4 = — 1 3 — 2 3 x 2 — 7 3 x 3 + 5 3 x 4 + ( — 2 5 ) ( — 5 3 x 2 + 11 3 x 3 — 4 3 x 4 ) = 23 3 + ( — 2 5 ) ( — 1 3 ) 13 3 x 2 — 4 3 x 3 + 5 3 x 4 + 13 5 ( — 5 3 x 2 + 11 3 x 3 — 4 3 x 4 ) = 14 3 + 13 5 ( — 1 3 ) ⇔

⇔ 3 x 1 + 2 x 2 + x 3 + x 4 = — 2 — 5 3 x 2 + 11 3 x 3 — 4 3 x 4 = — 1 3 — 19 5 x 3 + 11 5 x 4 = 39 5 41 5 x 3 — 9 5 x 4 = 19 5

Для того чтобы завершить прямой ход метода Гаусса, необходимо исключить x 3 из последнего уравнения системы — а 43 ( 2 ) а 33 ( 2 ) = — 41 5 — 19 5 = 41 19 :

3 x 1 + 2 x 2 + x 3 + x 4 = — 2 — 5 3 x 2 + 11 3 x 3 — 4 3 x 4 = — 1 3 — 19 5 x 3 + 11 5 x 4 = 39 5 41 5 x 3 — 9 5 x 4 = 19 5 ⇔

3 x 1 + 2 x 2 + x 3 + x 4 = — 2 — 5 3 x 2 + 11 3 x 3 — 4 3 x 4 = — 1 3 — 19 5 x 3 + 11 5 x 4 = 39 5 41 5 x 3 — 9 5 x 4 + 41 19 ( — 19 5 x 3 + 11 5 x 4 ) = 19 5 + 41 19 39 5 ⇔

⇔ 3 x 1 + 2 x 2 + x 3 + x 4 = — 2 — 5 3 x 2 + 11 3 x 3 — 4 3 x 4 = — 1 3 — 19 5 x 3 + 11 5 x 4 = 39 5 56 19 x 4 = 392 19

Обратный ход метода Гаусса:

• из последнего уравнения имеем: x 4 = 392 19 56 19 = 7 ;
• из 3-го уравнения получаем: x 3 = — 5 19 ( 39 5 — 11 5 x 4 ) = — 5 19 ( 39 5 — 11 5 × 7 ) = 38 19 = 2 ;
• из 2-го: x 2 = — 3 5 ( — 1 3 — 11 3 x 4 + 4 3 x 4 ) = — 3 5 ( — 1 3 — 11 3 × 2 + 4 3 × 7 ) = — 1 ;
• из 1-го: x 1 = 1 3 ( — 2 — 2 x 2 — x 3 — x 4 ) = — 2 — 2 × ( — 1 ) — 2 — 7 3 = — 9 3 = — 3 .

Ответ: x 1 = — 3 ; x 2 = — 1 ; x 3 = 2 ; x 4 = 7

Найти решение этого же примера методом Гаусса в матричной форме записи:

3 x 1 + 2 x 2 + x 3 + x 4 = — 2 x 1 — x 2 + 4 x 3 — x 4 = — 1 — 2 x 1 — 2 x 2 — 3 x 3 + x 4 = 9 x 1 + 5 x 2 — x 3 + 2 x 4 = 4

Расширенная матрица системы представлена в виде:

x 1 x 2 x 3 x 4 3 2 1 1 1 — 1 4 — 1 — 2 — 2 — 3 1 1 5 — 1 2 — 2 — 1 9 4

Прямой ход метода Гаусса в данном случае предполагает приведение расширенной матрицы к трапецеидальному виду при помощи элементарных преобразований. Этот процесс очень поход на процесс исключения неизвестных переменных в координатном виде.

Преобразование матрицы начинается с превращения всех элементов нулевые. Для этого к элементам 2-ой, 3-ей и 4-ой строк прибавляем соответствующие элементы 1-ой строки, которые умножены на — a 21 a 11 = — 1 3 , — a 31 a 11 = — — 2 3 = 2 3 и н а — а 41 а 11 = — 1 3 .

Дальнейшие преобразования происходит по такой схеме: все элементы во 2-ом столбце, начиная с 3-ей строки, становятся нулевыми. Такой процесс соответствует процессу исключения переменной . Для того, чтобы выполнить этой действие, необходимо к элементам 3-ей и 4-ой строк прибавить соответствующие элементы 1-ой строки матрицы, которая умножена на — а 32 ( 1 ) а 22 ( 1 ) = — 2 3 — 5 3 = — 2 5 и — а 42 ( 1 ) а 22 ( 1 ) = — 13 3 — 5 3 = 13 5 :

x 1 x 2 x 3 x 4 3 2 1 1 | — 2 0 — 5 3 11 3 — 4 3 | — 1 3 0 — 2 3 — 7 3 5 3 | 23 3 0 13 3 — 4 3 5 3 | 14 3

x 1 x 2 x 3 x 4

3 2 1 1 | — 2 0 — 5 3 11 3 — 4 3 | — 1 3 0 — 2 3 + ( — 2 5 ) ( — 5 3 ) — 7 3 + ( — 2 5 ) 11 3 5 3 + ( — 2 5 ) ( — 4 3 ) | 23 3 + ( — 2 5 ) ( — 1 3 ) 0 13 3 + 13 5 ( — 5 3 ) — 4 3 + 13 5 × 11 3 5 3 + 13 5 ( — 4 3 ) | 14 3 + 13 5 ( — 1 3 )

x 1 x 2 x 3 x 4

3 2 1 1 | — 2 0 — 5 3 11 3 — 4 3 | — 1 3 0 0 — 19 5 11 5 | 39 5 0 0 41 5 — 9 5 | 19 5

Теперь исключаем переменную x 3 из последнего уравнения — прибавляем к элементам последней строки матрицы соответствующие элементы последней строки, которая умножена на а 43 ( 2 ) а 33 ( 2 ) = — 41 5 — 19 5 = 41 19 .

x 1 x 2 x 3 x 4 3 2 1 1 | — 2 0 — 5 3 11 3 — 4 3 | — 1 3 0 0 — 19 5 11 5 | 39 5 0 0 41 5 — 9 5 | 19 5

x 1 x 2 x 3 x 4

3 2 1 1 | — 2 0 — 5 3 11 3 — 4 3 | — 1 3 0 0 — 19 5 11 5 | 39 5 0 0 41 5 + 41 19 ( — 19 5 ) — 9 5 + 41 19 × 11 5 | 19 5 + 41 19 × 39 5

x 1 x 2 x 3 x 4

3 2 1 1 | — 2 0 — 5 3 11 3 — 4 3 | — 1 3 0 0 — 19 5 11 5 | 39 5 0 0 0 56 19 | 392 19

Теперь применим обратных ход метода. В матричной форме записи такое преобразование матрицы, чтобы матрица, которая отмечена цветом на изображении:

x 1 x 2 x 3 x 4 3 2 1 1 | — 2 0 — 5 3 11 3 — 4 3 | — 1 3 0 0 — 19 5 11 5 | 39 5 0 0 0 56 19 | 392 19

стала диагональной, т.е. приняла следующий вид:

x 1 x 2 x 3 x 4 3 0 0 0 | а 1 0 — 5 3 0 0 | а 2 0 0 — 19 5 0 | а 3 0 0 0 56 19 | 392 19 , где а 1 , а 2 , а 3 — некоторые числа.

Такие преобразования выступают аналогом прямому ходу, только преобразования выполняются не от 1-ой строки уравнения, а от последней. Прибавляем к элементам 3-ей, 2-ой и 1-ой строк соответствующие элементы последней строки, которая умножена на

— 11 5 56 19 = — 209 280 , н а — — 4 3 56 19 = 19 42 и н а — 1 56 19 = 19 56 .

x 1 x 2 x 3 x 4 3 2 1 1 | — 2 0 — 5 3 11 3 — 4 3 | — 1 3 0 0 — 19 5 11 5 | 39 5 0 0 0 56 19 | 392 19

x 1 x 2 x 3 x 4

3 2 1 1 + ( — 19 56 ) 56 19 | — 2 + ( — 19 56 ) 392 19 0 — 5 3 11 3 — 4 3 + 19 42 × 56 19 | — 1 3 + 19 42 × 392 19 0 0 — 19 5 11 5 + ( — 209 280 ) 56 19 | 39 5 + ( — 209 280 ) 392 19 0 0 0 56 19 | 392 19

x 1 x 2 x 3 x 4

3 2 1 0 | — 9 0 — 5 3 11 3 0 | 9 0 0 — 19 5 0 | — 38 5 0 0 0 56 19 | 392 19

Далее прибавляем к элементам 2-ой и 1-ой строк соответствующие элементы 3-ей строки, которые умножены на

— 11 3 — 19 5 = 55 57 и н а — 1 — 19 5 = 5 19 .

x 1 x 2 x 3 x 4 3 2 1 0 | — 9 0 — 5 3 11 3 0 | 9 0 0 — 19 5 0 | — 38 5 0 0 0 56 19 | 392 19

x 1 x 2 x 3 x 4

3 2 1 + 5 19 ( — 19 5 ) 0 | — 9 + 5 19 ( — 38 5 ) 0 — 5 3 11 3 + 55 57 ( — 19 5 ) 0 | 9 + 55 57 ( — 38 5 ) 0 0 — 19 5 0 | — 38 5 0 0 0 56 19 | 392 19

x 1 x 2 x 3 x 4

3 2 1 0 | — 11 0 — 5 3 0 0 | 5 3 0 0 — 19 5 0 | — 38 5 0 0 0 56 19 | 392 19

На последнем этапе прибавляем элементы 2-ой строки к соответствующим элементам 1-ой строки, которые умножены на — 2 — 5 3 = 6 5 .

x 1 x 2 x 3 x 4 3 2 1 0 | — 11 0 — 5 3 0 0 | 5 3 0 0 — 19 5 0 | — 38 5 0 0 0 56 19 | 392 19

x 1 x 2 x 3 x 4

3 2 + 6 5 ( — 5 3 ) 0 0 | — 11 + 6 5 × 5 3 ) 0 — 5 3 0 0 | 5 3 0 0 — 19 5 0 | — 38 5 0 0 0 56 19 | 392 19

x 1 x 2 x 3 x 4

3 0 0 0 | — 9 0 — 5 3 0 0 | 5 3 0 0 — 19 5 0 | — 38 5 0 0 0 56 19 | 392 19

Полученная матрица соответствует системе уравнений

3 x 1 = — 9 — 5 3 x 2 = 5 3 — 19 5 x 3 = — 38 5 56 19 x 4 = 392 19 , откуда находим неизвестные переменные.

Ответ: x 1 = — 3 , x 2 = — 1 , x 3 = 2 , x 4 = 7 . ​​​

Видео:Решение системы линейных уравнений методом ГауссаСкачать

Описание алгоритма использования метода Гаусса для решения СЛАУ с несовпадающим количеством уравнений и неизвестных, или с вырожденной системой матрицы

Если основная матрица квадратная или прямоугольная, то системы уравнений могут иметь единственное решение, могут не иметь решений, а могут иметь бесконечное множество решений.

Из данного раздела мы узнаем, как с помощью метода Гаусса определить совместность или несовместность СЛАУ, а также, в случае совместности, определить количество решений для системы.

В принципе, метод исключения неизвестных при таких СЛАУ остается таким же, однако есть несколько моментов, на которых необходимо заострить внимание.

На некоторых этапах исключения неизвестных, некоторые уравнения обращаются в тождества 0=0. В таком случае, уравнения можно смело убрать из системы и продолжить прямой ход метода Гаусса.

Если мы исключаем из 2-го и 3-го уравнения x 1 , то ситуация оказывается следующей:

x 1 + 2 x 2 — x 3 + 3 x 4 = 7 2 x 1 + 4 x 2 — 2 x 3 + 6 x 4 = 14 x — x + 3 x + x = — 1 ⇔

x 1 + 2 x 2 — x 3 + 3 x 4 = 7 2 x 1 + 4 x 2 — 2 x 3 + 6 x 4 + ( — 2 ) ( x 1 + 2 x 2 — x 3 + 3 x 4 ) = 14 + ( — 2 ) × 7 x — x + 3 x + x + ( — 1 ) ( x 1 + 2 x 2 — x 3 + 3 x 4 ) = — 1 + ( — 1 ) × 7 ⇔

⇔ x 1 + 2 x 2 — x 3 + 3 x 4 = 7 0 = 0 — 3 x 2 + 4 x 3 — 2 x 4 = — 8

Из этого следует, что 2-ое уравнение можно смело удалять из системы и продолжать решение.

Если мы проводим прямой ход метода Гаусса, то одно или несколько уравнений может принять вид — некоторое число, которое отлично от нуля.

Это свидетельствует о том, что уравнение, обратившееся в равенство 0 = λ , не может обратиться в равенство ни при каких любых значениях переменных. Проще говоря, такая система несовместна (не имеет решения).

• В случае если при проведении прямого хода метода Гаусса одно или несколько уравнений принимают вид 0 = λ , где λ — некоторое число, которое отлично от нуля, то система несовместна.
• Если же в конце прямого хода метода Гаусса получается система, число уравнений которой совпадает с количеством неизвестных, то такая система совместна и определена: имеет единственное решение, которое вычисляется обратным ходом метода Гаусса.
• Если при завершении прямого хода метода Гаусса число уравнений в системе оказывается меньше количества неизвестных, то такая система совместна и имеет бесконечно количество решений, которые вычисляются при обратном ходе метода Гаусса.

🔍 Видео

Математика без Ху!ни. Метод Гаусса. Совместность системы. Ранг матрицы.Скачать

Метод Гаусса Пример РешенияСкачать

12. Решение систем линейных уравнений методом ГауссаСкачать

Линейная алгебра, 9 урок, Метод ГауссаСкачать

Решение системы уравнений методом Гаусса. Бесконечное множество решенийСкачать

решение системы уравнений методом ГауссаСкачать

Линейная алгебра, Матрицы: Метод Гаусса. Высшая математикаСкачать

Метод Жордана-Гаусса (метод прямоугольников). ВидеоурокСкачать

12. Метод Гаусса решения систем линейных уравнений. Часть 1.Скачать

Общее, частное, базисное решение системы линейных уравнений Метод ГауссаСкачать

МЕТОД ГАУССА 😉 #егэ #математика #профильныйегэ #shorts #огэСкачать

6 способов в одном видеоСкачать

Метод Крамера за 3 минуты. Решение системы линейных уравнений - bezbotvyСкачать