- Решение нелинейных уравнений
- Отделение корней нелинейного уравнения
- Уточнение корней нелинейного уравнения
- Решение систем уравнений
- Системы линейных алгебраических уравнений
- Решение систем нелинейных уравнений
- Контрольная работа: Решение нелинейных уравнений
- Численные методы решения нелинейных уравнений. Метод хорд.
- Численные методы решения нелинейных уравнений. Метод хорд.
- Пример решения уравнений методом хорд
- 📺 Видео
Видео:1,2 Решение нелинейных уравнений методом хордСкачать

Решение нелинейных уравнений
Вычисление корней численными методами включает два основных этапа:
· уточнение корней до заданной точности.
Рассмотрим эти два этапа подробно.
Отделение корней нелинейного уравнения
Учитывая легкость построения графиков функций в MathCAD , в дальнейшем будет использоваться графический метод отделения корней.
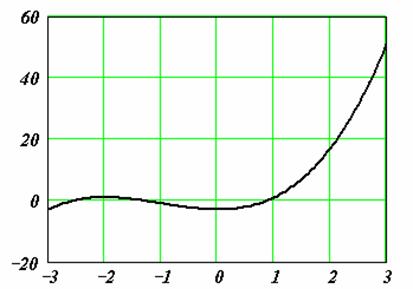
Пример. Дано алгебраическое уравнение
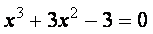
Определить интервалы локализации корней этого уравнения.
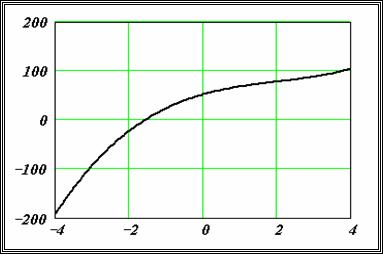
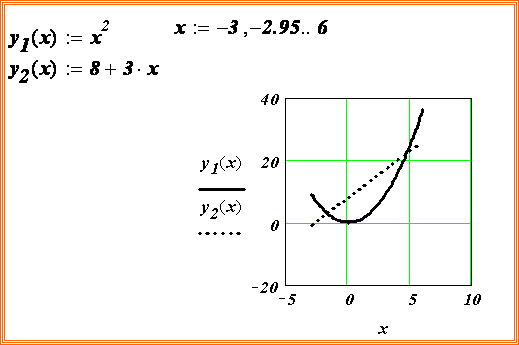
Пример. Дано алгебраическое уравнение
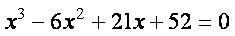
Определить интервалы локализации корней этого уравнения.
На рисунке приведен график функции 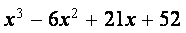
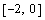
Уточнение корней нелинейного уравнения
Для уточнения корня используются специальные вычислительные методы такие, как метод деления отрезка пополам, метод хорд, метод касательных (метод Ньютона) и многие другие.
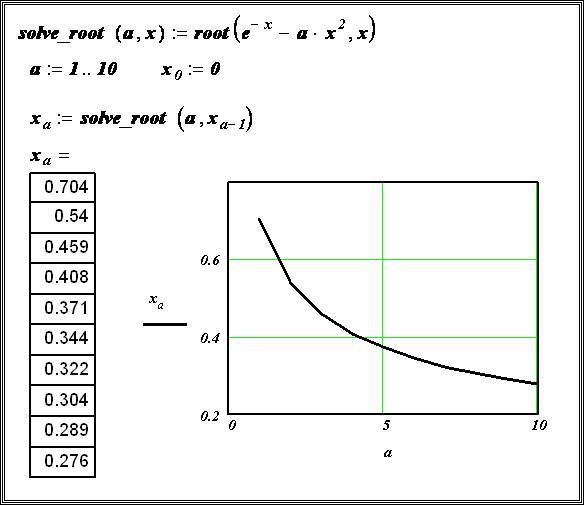
Функция root . В MathCAD для уточнения корней любого нелинейного уравнения (не обязательно только алгебраического) введена функция root , которая может иметь два или четыре аргумента, т.е. 

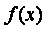
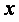
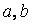
Пример. Используя функцию 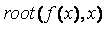
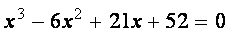
Заметим, что для вычисления всех трех корней использовался прием понижения порядка алгебраического уравнения, рассмотренный в п. 8.1.1. ¨
Функция root с двумя аргументами требует задания (до обращения к функции) переменной 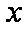
Пример 8.1.5. Используя функцию root , вычислить изменения корня нелинейного уравнения 
Функция polyroots . Для вычисления всех корней алгебраического уравнения порядка 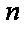
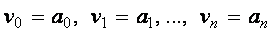
Пример. Используя функцию polyroots , найти все три корня уравнения 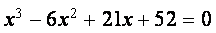
Блок Given . При уточнении корня нелинейного уравнения можно использовать специальный вычислительный блок Given , имеющий следующую структуру:
Решаемое уравнение задается в виде равенства, в котором используется «жирный» знак равно, вводимый с палитры Логический .
Ограничения содержат равенства или неравенства, которым должен удовлетворять искомый корень.
Функция Find уточняет корень уравнения, вызов этой функции имеет вид Find ( x ), где x – переменная, по которой уточняется корень. Если корня уравнения на заданном интервале не существует, то следует вызвать функцию Minerr ( x ), которая возвращает приближенное значение корня.
Для выбора алгоритма уточнения корня необходимо щелкнуть правой кнопкой мыши на имени функции Find ( x ) и в появившемся контекстном меню (см. рисунок) выбрать подходящий алгоритм.
Аналогично можно задать алгоритм решения и для функции Minerr ( x ).
Использование численных методов в функциях Find ( x ), Minerr ( x ) требует перед блоком Given задать начальные значения переменным, по которым осуществляется поиск корней уравнения.
Пример. Используя блок Given , вычислите корень уравнения 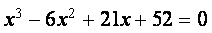
Видео:Метод Ньютона (метод касательных) Пример РешенияСкачать

Решение систем уравнений
В зависимости от того, какие функции входят в систему уравнений, можно выделить два класса систем:
· алгебраические системы уравнений;
· трансцендентные системы уравнений.
Среди алгебраических систем уравнений особое место занимают системы линейных алгебраических уравнений (СЛАУ).
Системы линейных алгебраических уравнений
Системой линейных алгебраических уравнений (СЛАУ) называется система вида:
В матричном виде систему можно записать как
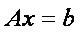
где 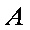
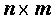
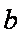

Для вычисления решения СЛАУ следует использовать функцию lsolve , обращение к которой имеет вид: lsolve (А, b ), где А – матрица системы, 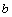
Решение систем нелинейных уравнений
MathCAD дает возможность находить решение системы уравнений численными методами, при этом максимальное число уравнений в MathCAD 2001 i доведено до 200.
Для решения системы уравнений необходимо выполнить следующие этапы.
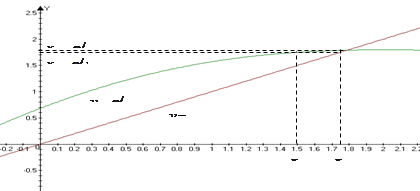
Задание начального приближения для всех неизвестных, входящих в систему уравнений. При небольшом числе неизвестных этот этап можно выполнить графически, как показано в примере.
Пример. Дана система уравнений:
Определить начальные приближения для решений этой системы.
Видно, что система имеет два решения: для первого решения в качестве начального приближения может быть принята точка (-2, 2), а для второго решения – точка (5, 20). ¨
Вычисление решения системы уравнений с заданной точностью . Для этого используется уже известный вычислительный блок Given .
Функция Find вычисляет решение системы уравнений с заданной точностью, и вызов этой функции имеет вид Find ( x ), где x – список переменных, по которым ищется решение. Начальные значения этим переменным задаются в блоке . Число аргументов функции должно быть равно числу неизвестных.
Следующие выражения недопустимы внутри блока решения:
· ограничения со знаком ¹ ;
· дискретная переменная или выражения, содержащие дискретную переменную в любой форме;
· блоки решения уравнений не могут быть вложены друг в друга, каждый блок может иметь только одно ключевое слово Given и имя функции Find (или Minerr ).
Пример. Используя блок Given , вычислить все решения системы предыдущего примера. Выполнить проверку найденных решений.
Пример. Используя функцию 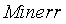
Видео:Решение нелинейного уравнения методом хорд (секущих) (программа)Скачать

Контрольная работа: Решение нелинейных уравнений
| Название: Решение нелинейных уравнений Раздел: Рефераты по математике Тип: контрольная работа Добавлен 09:13:39 31 декабря 2010 Похожие работы Просмотров: 3535 Комментариев: 14 Оценило: 7 человек Средний балл: 4.1 Оценка: 4 Скачать |

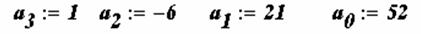
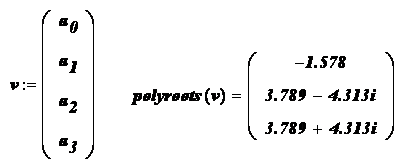



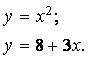

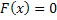
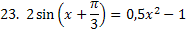

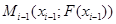 и
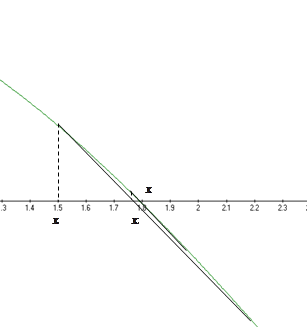
и 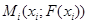 построить прямую
построить прямую  (то есть хорду, соединяющую две точки графика
(то есть хорду, соединяющую две точки графика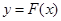 ) и взять в качестве следующего приближения
) и взять в качестве следующего приближения 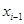 абсциссу точки пересечения этой прямой с осью Ox .
абсциссу точки пересечения этой прямой с осью Ox .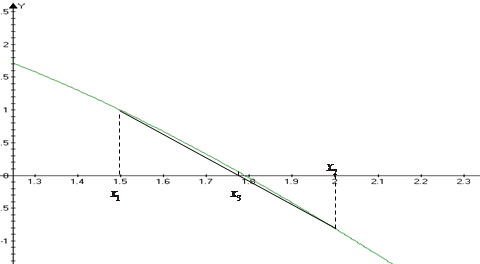

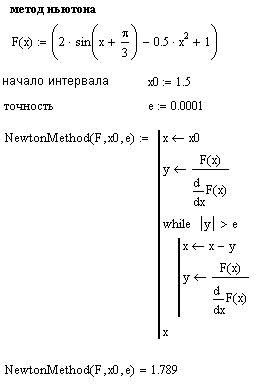

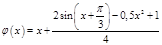

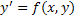 на отрезке [a,b] при начальном заданном условии
на отрезке [a,b] при начальном заданном условии 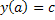 и шаге интегрирования h:
и шаге интегрирования h: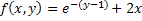


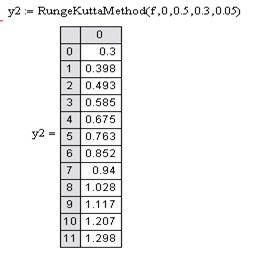


 . Итерационный процесс выполняется до того момента, пока не будет достигнута заданная точность
. Итерационный процесс выполняется до того момента, пока не будет достигнута заданная точность  .
. хордой, проходящей через точки
хордой, проходящей через точки  и
и  (см. рис.1.).
(см. рис.1.).
 .
.
 и
и  , соответственно.
, соответственно. записанное выше уравнение перепишется в следующем виде:
записанное выше уравнение перепишется в следующем виде:
 или
или  , на концах которого функция
, на концах которого функция  или
или  .
. .
.
 одним из методов отделения корней. З адать погрешность расчета (малое положительное число
одним из методов отделения корней. З адать погрешность расчета (малое положительное число  ) .
) .
 ,
,  и
и  . Далее необходимо проверить два условия:
. Далее необходимо проверить два условия: , то искомый корень находится внутри левого отрезка положить
, то искомый корень находится внутри левого отрезка положить  ,
,  ;
; , то искомый корень находится внутри правого отрезка принять
, то искомый корень находится внутри правого отрезка принять  ,
,  .
.

 , то необходимо продолжить итерационный процесс
, то необходимо продолжить итерационный процесс  и перейти к п.2 рассматриваемого алгоритма.
и перейти к п.2 рассматриваемого алгоритма.
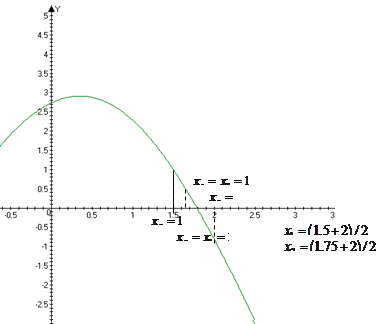
 методом хорд. Корень необходимо найти в рассматриваемом диапазоне
методом хорд. Корень необходимо найти в рассматриваемом диапазоне  с точностью
с точностью  .
.

 .
.

 алгоритм поиска может быть упрощен. Предположим, что вторая производная
алгоритм поиска может быть упрощен. Предположим, что вторая производная  0,
0, 0″ width=»158″ height=»20″ border=»0″ />
0″ width=»158″ height=»20″ border=»0″ /> 0″ width=»122″ height=»20″ border=»0″ /> , где
0″ width=»122″ height=»20″ border=»0″ /> , где  или
или  .
.

 , где k =0,1,2,…
, где k =0,1,2,…
 , где k =0,1,2,…
, где k =0,1,2,… сводится к рассматриваемому , если уравнение записать в форме:
сводится к рассматриваемому , если уравнение записать в форме:  .
.












