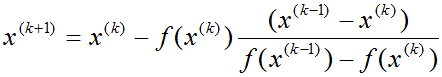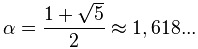Привет! Сегодня посмотрим, как приближённо решать уравнения с помощью метода касательных (алгоритма Ньютона).
И напишем программу на языке программирования C#.
Пусть дано нелинейное уравнение: f(x) = 0 (Если уравнение будет линейное, то невозможно будет провести касательную). Метод касательных поможет приближённо найти корень уравнения на отрезке [a, b], при условии, что функция непрерывна на замкнутом интервале [a, b], и корень на этом отрезке только один! А так же функция не меняет свою вогнутость или выпуклость (постоянный знак второй производной) и не имеет экстремумов (первая производная не равна нулю) на отрезке [a, b].
Графически функция может выглядеть следующим образом:
Т.е. самая стандартная функция.
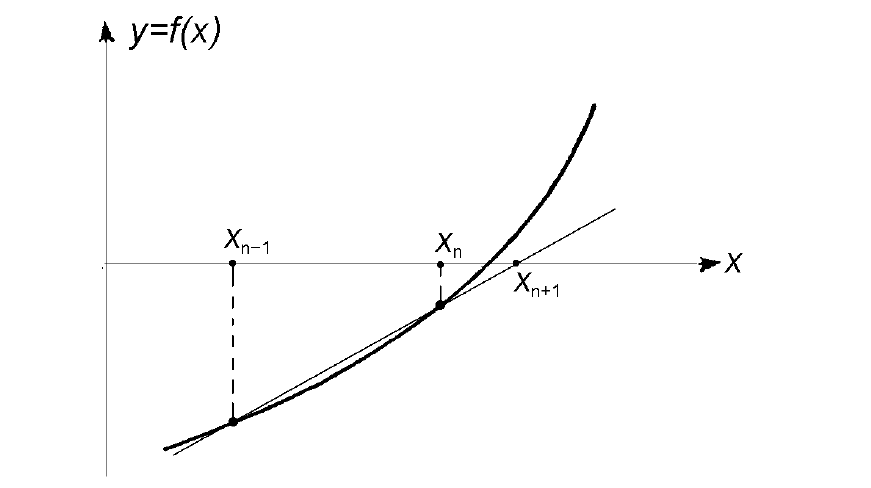
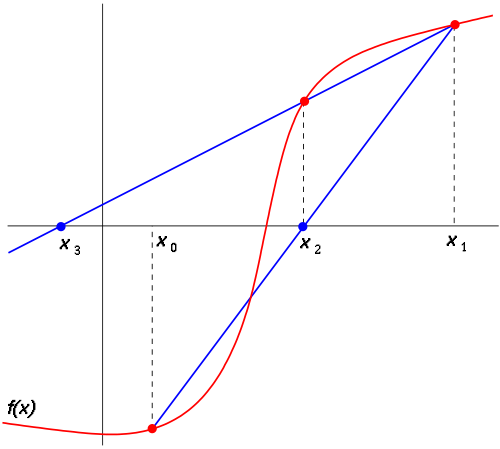
Графическая интерпретация метода Ньютона:
От x0 узнаём значение функции. В этой точке проводим касательную. Касательная пересекает ось X, и мы получаем новую точку x1. И начинаем всё сначала. Числа x0, x1, x2 и т.д. приближаются к корню уравнения.
Выведем формулу для xn.
Приравняем к нулю (пересечение с осью X) и выразим x.
Погрешность данного метода ε > |xn+1 — xn|. Причём самая первая точка x0 не берётся во внимание при определении погрешности. Т.е. если |xn+1 — xn| меньше, чем заданное значение ε, то можно прекращать вычисления.
За саму первую точку x0 берут либо начало отрезка a, либо конец отрезка b. Это зависит от возрастания или убывания функции, а так же, в какую сторону выпукла функция.
Удобно пользоваться правилом:
Для примера, найдём положительный корень уравнения: x 2 = 2
Определим отрезок [1, 2], где будем искать корень.
Функция f(x) = x 2 — 2
f′′(x) = 2
f(2) = 4 — 2 = 2
Определим корень уравнения с точностью до ε=0.001 на языке программирования C#.
Т.к. x0 — не участвует при вычислении погрешности, то мы в начале до цикла while вычисляем xn и xn+1 (xnp1). Т.к. тип данных double, то чтобы возвести число в степень, используем специальную функцию Math.Pow(). В условии цикла while мы используем разницу без модуля, потому что мы идём от правого конца отрезка, и xn всегда больше, чем xnp1.
Видео:Метод Ньютона (метод касательных) Пример РешенияСкачать
Программирование на C, C# и Java
Видео:После этого видео, ТЫ РЕШИШЬ ЛЮБУЮ Систему Нелинейных УравненийСкачать
Уроки программирования, алгоритмы, статьи, исходники, примеры программ и полезные советы
ОСТОРОЖНО МОШЕННИКИ! В последнее время в социальных сетях участились случаи предложения помощи в написании программ от лиц, прикрывающихся сайтом vscode.ru. Мы никогда не пишем первыми и не размещаем никакие материалы в посторонних группах ВК. Для связи с нами используйте исключительно эти контакты: vscoderu@yandex.ru, https://vk.com/vscode
Видео:Решение уравнений (метод дихотомии) на C#Скачать
Метод хорд
Метод хорд используется для численного нахождения приближенного значения корня нелинейного уравнения. В данной статье будет показан алгоритм метода, а также будет приведена его программная реализация на языках: Си, C# и Java.
Метод хорд (то же, что метод секущих) — итерационный метод решения нелинейного уравнения.
Нелинейное уравнение — это уравнение в котором есть хотя бы один член, включающий неизвестное, НЕ в первой степени. Обозначается, как: f(x) = 0.
Метод хорд. Алгоритм
Метод хорд является итерационным алгоритмом, таким образом решение уравнения заключается в многократном повторении этого алгоритма. Полученное в результате вычислений решение является приближенным, но его точность можно сделать такой, какой требуется, задав нужное значение погрешности ε. В начале вычислений методом хорд требуется указать границы области поиска корня; в общем случае эта граница может быть произвольной.
Итерационная формула для вычислений методом хорд следующая:
Вычисления продолжаются до тех пор, пока не станет истинным выражение:
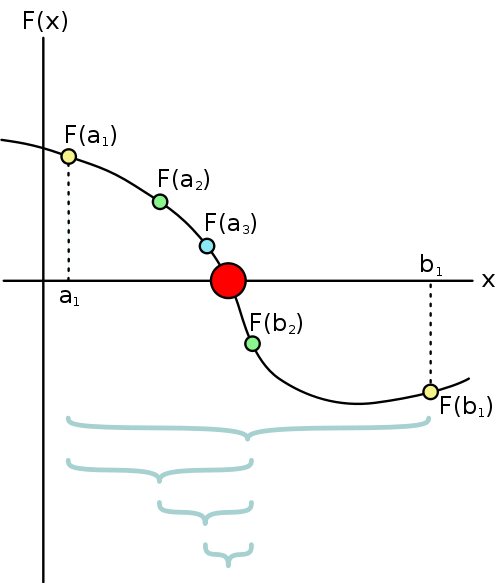
Геометрическая модель одного шага итераций метода хорд представлена на рисунке:
Метод хорд, в отличие от метода Ньютона, имеет плюс в том, что для расчета не требуется вычисление производных. Но при этом метод хорд медленнее, его сходимость равна золотому сечению:
Метод хорд. Программная реализация
Ниже мы приводим реализацию алгоритма метода хорд на языках программирования Си, C# и Java. Кроме того, исходники программ доступны для скачивания.
В качестве примера ищется корень уравнения x 3 — 18x — 83 = 0 в области x0 = 2, x1 = 10, с погрешностью e = 0.001. (Корень равен: 5.7051).
x_prev — это xk-1, x_curr — это xk, x_next — это xk+1.
Видео:1 3 Решение нелинейных уравнений методом простых итерацийСкачать
Поиск по сайту
В прошлой статье мы говорили о решении специальных типов уравнений с помощью точных методов. Сегодня же поговорим о приближенных (численных) методах решения уравнений вида f(x)=0.
В листингах программ есть записи вида:
которые соответствуют процедуре получения значения функции, записанной в виде математического выражения в точке x. Фактически, функция Function реализует парсер функций.
Видео:C# ФУНКЦИИ И МЕТОДЫ | МЕТОД C# ЧТО ЭТО | ФУНКЦИИ C# ПРИМЕР | C# ОТ НОВИЧКА К ПРОФЕССИОНАЛУ | # 35Скачать
Метод половинного деления
Другие названия: метод бисекции (bisection method), метод дихотомии.
Метод половинного деления – простейший численный метод для решения нелинейных уравнений вида f(x)=0, где функция f(x) должна быть непрерывной на искомом отрезке [xL; xR], причем функция должна принимать значения разных знаков, т.е. должно выполняться условие:
С непрерывности функции f(x) следует, что на интервале [xL; xR] существует, по крайней мере, один корень уравнения (если их несколько, то метод находит один из них).
Выберем точку – середину интервала:
Если f(xM) = 0, то корень найден. Если f(x)≠0, то разобьем этот интервал на два: [xL; xM] и [xM; xR].
Теперь найдем новый интервал, на котором функция изменяет знак. Повторим описанную процедуру до тех пор, пока не получим требуемую точность или превысим максимально допустимое количество итераций.
Геометрическая интерпретация метода:
Реализация метода на C#:
Видео:Решение слау методом итераций. Метод простых итераций c++.Скачать
Метод секущих
Другие названия: метод хорд (secant method);
Метод хорд – еще один численный метод для решения нелинейных уравнений вида f(x)=0, где функция f(x) должна быть непрерывной на искомом отрезке [x0; x1], причем функция должна принимать значения разных знаков, т.е. должно выполняться условие:
Последующие приближения находят по формуле:
Геометрическая интерпретация метода:
Реализация метода на C#:
Видео:Метод касательных (алгоритм Ньютона) на C#Скачать
Метод простых итераций
Уравнение f(x)=0 с помощью некоторых преобразований необходимо переписать в виде x=φ(x).
Уравнение f(x)=0 эквивалентно уравнению x=x+λ(x)f(x) для любой функции λ(x)≠0. Возьмем φ(x)=x-λ(x)f(x) и выберем функцию (или переменную) λ(x)≠0 так, чтобы функция φ(x) удовлетворяла необходимым условиям.
Для нахождения корня уравнения x=φ(x) выберем некоторое начальное значение x0, которое должно находиться как можно ближе к корню уравнения. Дальше с помощью итерационной формулы xn+1=φ(xn) будем находить каждое следующее приближение корня уравнения.
Пример: x 2 -5x+6=0
Преобразования в вид x=φ(x):
Реализация метода на C#:
Видео:ОПЕРАТОРЫ. АРИФМЕТИЧЕСКИЕ ОПЕРАЦИИ С ЧИСЛАМИ В C# | C# ОТ НОВИЧКА К ПРОФЕССИОНАЛУ | Урок # 8Скачать
Метод Вегштейна
Метод Вегштейна является модификацией метода секущих, однако его можно назвать и улучшенным методом простой итерации, преобразовав вычислительную формулу к виду:
Это двухшаговый метод, и для начала вычислений необходимо задать 2 приближения xa и xb.
Реализация метода на C#:
public static double Wegstein(string expression, double xa, double xb, double epsilon = 0.00001) < double x = 0.0;
Видео:6 Метод половинного деления C++ Численные методы решения нелинейного уравненияСкачать
Метод Ньютона
Если 
— начальное приближение корня уравнения f(x) = 0, то последовательные приближения находят по формуле:
Если f’ и f» непрерывны и сохраняют определенные знаки на отрезке 
, а f(a)f(b)
🎥 Видео
10 Численные методы решения нелинейных уравненийСкачать
FreeDy010 Решение Системы нелинейных уравнений scipy sympyСкачать
Уроки C++. Простые линейные уравненияСкачать
Метод половинного деления. ДихотомияСкачать
МЗЭ 2021 Лекция 11 Метод Ньютона для решения систем нелинейных уравненийСкачать
C# уроки для начинающих # Язык си шарп - Переменные, алгебра, литералы, методыСкачать
Алгоритмы С#. Метод Ньютона для решения систем уравненийСкачать
ИНИЦИАЛИЗАЦИЯ МАССИВА | СПОСОБЫ | СИ ШАРП | C# ПРИМЕРЫ | C# ОТ НОВИЧКА К ПРОФЕССИОНАЛУ | # 25Скачать
10 Метод Ньютона (Метод касательных) C++ Численные методы решения нелинейного уравненияСкачать
Способы решения систем нелинейных уравнений. 9 класс.Скачать
