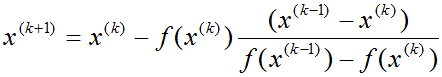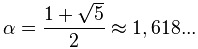Решение нелинейных уравнений методом хорд python

Видео:Алгоритмы. Нахождение корней уравнения методом хордСкачать

Программирование на C, C# и Java

Видео:Метод Ньютона (метод касательных) Пример РешенияСкачать

Уроки программирования, алгоритмы, статьи, исходники, примеры программ и полезные советы

ОСТОРОЖНО МОШЕННИКИ! В последнее время в социальных сетях участились случаи предложения помощи в написании программ от лиц, прикрывающихся сайтом vscode.ru. Мы никогда не пишем первыми и не размещаем никакие материалы в посторонних группах ВК. Для связи с нами используйте исключительно эти контакты: vscoderu@yandex.ru, https://vk.com/vscode

Видео:1,2 Решение нелинейных уравнений методом хордСкачать

Метод хорд

Метод хорд используется для численного нахождения приближенного значения корня нелинейного уравнения. В данной статье будет показан алгоритм метода, а также будет приведена его программная реализация на языках: Си, C# и Java.

Метод хорд (то же, что метод секущих) — итерационный метод решения нелинейного уравнения.

Нелинейное уравнение — это уравнение в котором есть хотя бы один член, включающий неизвестное, НЕ в первой степени. Обозначается, как: f(x) = 0.

Метод хорд. Алгоритм

Метод хорд является итерационным алгоритмом, таким образом решение уравнения заключается в многократном повторении этого алгоритма. Полученное в результате вычислений решение является приближенным, но его точность можно сделать такой, какой требуется, задав нужное значение погрешности ε. В начале вычислений методом хорд требуется указать границы области поиска корня; в общем случае эта граница может быть произвольной.

Итерационная формула для вычислений методом хорд следующая:

Вычисления продолжаются до тех пор, пока не станет истинным выражение:

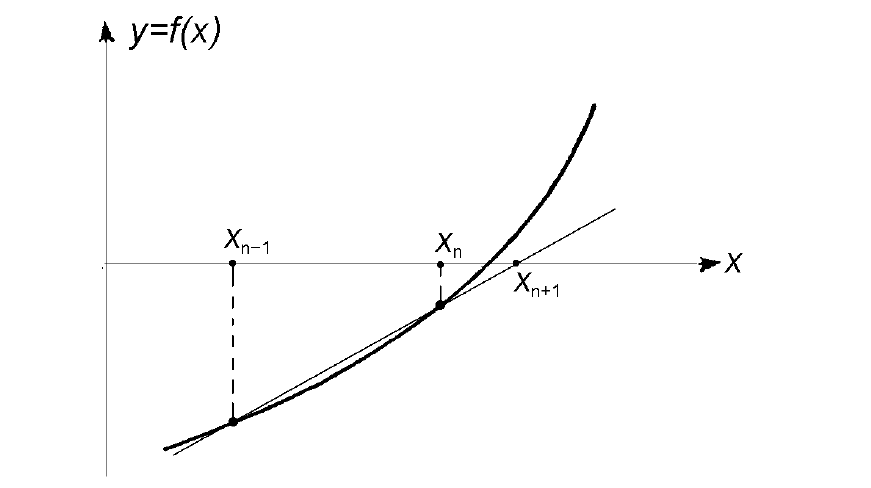
Геометрическая модель одного шага итераций метода хорд представлена на рисунке:

Метод хорд, в отличие от метода Ньютона, имеет плюс в том, что для расчета не требуется вычисление производных. Но при этом метод хорд медленнее, его сходимость равна золотому сечению:

Метод хорд. Программная реализация

Ниже мы приводим реализацию алгоритма метода хорд на языках программирования Си, C# и Java. Кроме того, исходники программ доступны для скачивания.

В качестве примера ищется корень уравнения x 3 — 18x — 83 = 0 в области x0 = 2, x1 = 10, с погрешностью e = 0.001. (Корень равен: 5.7051).

x_prev — это x_k-1, x_curr — это x_k, x_next — это x_k+1.

Видео:Решение n го нелинейных алгебраических уравнений в PythonСкачать

Решение нелинейных уравнений в Python

у меня 4 нелинейных уравнения с тремя неизвестными X , Y и Z что я хочу решить для. Уравнения имеют вид:

. где a , b и c — константы, которые зависят от каждого значения F в четырех уравнений.

каков наилучший способ решить эту проблему?

Видео:Решение нелинейного уравнения методом хорд (секущих) (программа)Скачать

2 ответов

есть два способа сделать это.

1. используйте нелинейный решатель
2. Линеаризовать задачу и решать ее в наименьших квадратов смысла

Видео:Численное решение уравнений, урок 3/5. Метод хордСкачать

настройка

Итак, как я понимаю ваш вопрос, вы знаете F, a, b и c в 4 разных точках, и вы хотите инвертировать для параметров модели X, Y и Z. У нас есть 3 неизвестных и 4 наблюдаемых точки данных, поэтому проблема переопределена. Поэтому мы будем решать в метода наименьших квадратов.

в этом случае чаще используется противоположная терминология,поэтому давайте перевернем ваше уравнение. Вместо:

откуда мы знаем!—10—>, X , Y и Z в 4 разных точках (например, F_0, F_1, . F_i ).

мы просто меняем имена переменных, а не само уравнение. (Это больше для моего удобства, чем ничего еще.)

Видео:Решение нелинейных уравнений методом хордСкачать

Линейный Решением

это на самом деле можно линеаризовать это уравнение. Вы можете легко решить для a^2 , b^2 , a b cos(c) и a b sin(c) . Чтобы сделать это немного проще, давайте еще раз перечислим вещи:

теперь уравнение намного проще: F_i = d + e X_i + f Y_i + g Z_i . Легко сделать линейную инверсию наименьших квадратов для d , e , f и g . Тогда мы сможем получить a , b и c от:

Хорошо, давайте запишем это в матричной форме. Мы собираемся перевести 4 наблюдения (код, который мы напишем, будет принимать любое количество наблюдений, но давайте сохраним его конкретным на данный момент):

или: F = G * m (я geophysist, поэтому мы используем G для «функций Грина» и m для «параметры модели». Обычно мы использовали d для «данных» вместо F , так же.)

In python, это переводится на:

Видео:Решение нелинейного уравнения методом Ньютона (касательных) (программа)Скачать

нелинейное решение

вы также можете решить эту проблему с помощью scipy.optimize , как предложил @Joe. Самая доступная функция в scipy.optimize is scipy.optimize.curve_fit который использует метод Levenberg-Marquardt по умолчанию.

Levenberg-Marquardt-это алгоритм «восхождения на холм» (ну, в этом случае он идет вниз, но термин все равно используется). В некотором смысле вы делаете первоначальное предположение о параметрах модели (все они, по умолчанию в scipy.optimize ) и следуйте по склону observed — predicted в пространстве параметров вниз до дна.

предостережение: выбор правильного метода нелинейной инверсии, начальная догадка и настройка параметров метода-это очень «темное искусство». Вы только узнаете это, делая это, и есть много ситуаций, когда вещи не будут работать должным образом. Levenberg-Marquardt-хороший общий метод, если ваше пространство параметров довольно гладкое (это должно быть). Есть много другие (включая генетические алгоритмы, нейронные сети и т. д. В дополнение к более распространенным методам, таким как имитационный отжиг), которые лучше в других ситуациях. Я не собираюсь углубляться в эту часть.

есть один общий gotcha, что некоторые инструменты оптимизации пытаются исправить для этого scipy.optimize не пытается справиться. Если параметры модели имеют разные значения (например, a=1, b=1000, c=1e-8 ), вам нужно будет масштабировать вещи так, чтобы они были похожи по величине. В противном случае scipy.optimize ‘ы алгоритмы «восхождения на холм» (например, LM) не будут точно вычислять оценку локального градиента и дадут дико неточные результаты. На данный момент, я предполагаю, что a , b и c относительно аналогичных величин. Кроме того, имейте в виду, что по существу все нелинейные методы требуют от вас сделать первоначальное предположение и чувствительны к этому предположению. Я оставляю его ниже (просто передайте его как p0 kwarg к curve_fit ) потому что по умолчанию a, b, c = 1, 1, 1 — это довольно точный думаю для a, b, c = 3, 2, 1 .

с оговорками в сторону, curve_fit ожидает, что будет передана функция, набор точек, где были сделаны наблюдения (как один ndim x npoints array) и наблюдаемые значения.

Итак, если мы напишем функцию следующим образом:

нам нужно обернуть его, чтобы принять немного разные аргументы, прежде чем передавать его curve_fit .

Видео:Метод хордСкачать

автономный пример двух методы:

даст вам полную реализацию, вот пример

1. генерирует случайно распределенные точки для оценки функции on,
2. оценивает функцию на этих точках (используя параметры модели set),
3. добавляет шума к результатам,
4. а затем инвертирует параметры модели, используя как линейные, так и нелинейные методы, описанные выше.

Видео:Численные методы (1 урок)(Решение нелинейных уравнений. Метод дихотомии. Python)Скачать

Как решить пару нелинейных уравнений с использованием Python?

Каков наилучший способ решения пары нелинейных уравнений с использованием Python. (Numpy, Scipy или Sympy)

Фрагмент кода, который решает вышеупомянутую пару, будет отличным

Видео:Вычислительная математика. Метод касательных на Python(1 практика).Скачать

ОТВЕТЫ

Ответ 1

для численного решения, вы можете использовать fsolve:

Ответ 2

Если вы предпочитаете sympy, вы можете использовать nsolve.

Первый аргумент — это список уравнений, второй — список переменных, а третий — исходное предположение.

Ответ 3

Попробуйте это, я заверяю вас, что он будет работать отлично.

FYI. как упоминалось выше, вы также можете использовать «приближение Бройдена», заменив «fsolve» на «broyden1». Оно работает. Я сделал это.

Я точно не знаю, как работает приближение Бройдена, но это заняло 0,02 с.

И я рекомендую вам не использовать функции Sympy

Ответ 4

Ответ 5

Вы можете использовать пакет openopt и его метод NLP. Он имеет множество алгоритмов динамического программирования для решения нелинейных алгебраических уравнений, состоящих из:
goldenSection, scipy_fminbound, scipy_bfgs, scipy_cg, scipy_ncg, amsg2p, scipy_lbfgsb, scipy_tnc, bobyqa, ralg, ipopt, scipy_slsqp, scipy_cobyla, lincher, algencan,, которые вы можете выбрать.
Некоторые из последних алгоритмов могут решить проблему ограниченного нелинейного программирования. Итак, вы можете ввести свою систему уравнений в openopt.NLP() с такой функцией:

lambda x: x[0] + x[1]**2 — 4, np.exp(x[0]) + x[0]*x[1]

Ответ 6

Я получил метод Бройдена для работы с связанными нелинейными уравнениями (как правило, с участием многочленов и экспонент) в IDL, но я не пробовал его в Python:

Найти корень функции, используя первое приближение Я. Я. Брайденса.

Этот метод также известен как «хороший метод Бройденса».

Ответ 7

Альтернативой fsolve является root :

Если вы затем проверите

подтверждая правильность решения.

Ответ 8

Видео:Решение 1 го нелинейного алгебраического уравнения в PythonСкачать

Краткий ответ: используйте fsolve

Как упоминалось в других ответах, самое простое решение конкретной поставленной вами проблемы — использовать что-то вроде fsolve :

Видео:Метод простых итераций пример решения нелинейных уравненийСкачать

Аналитические решения?

Вы говорите, как «решить», но есть разные варианты решения. Поскольку вы упоминаете SymPy, я должен указать на самое большое различие между тем, что это может означать, а именно между аналитическими и числовыми решениями. Конкретный пример, который вы привели, не имеет (простого) аналитического решения, как другие системы нелинейных уравнений. Когда есть доступные аналитические решения, SymPY часто может найти их для вас:

Обратите внимание, что в этом примере SymPy находит все решения и не требует предварительной оценки.

Видео:Метод касательных (метод Ньютона)Скачать

Точность числовых решений

Однако большинство систем нелинейных уравнений не будет иметь подходящего аналитического решения, поэтому использование SymPy, как описано выше, прекрасно, когда оно работает, но не всегда применимо. Вот почему мы в конечном итоге ищем числовые решения, хотя и с числовыми решениями: 1) У нас нет гарантии, что мы нашли все решения или «правильное» решение, когда их много. 2) Мы должны предоставить первоначальное предположение, которое не всегда легко.

Приняв, что нам нужны числовые решения, что-то вроде fsolve , как правило, сделает все, что вам нужно. Для такого рода проблем SymPy, вероятно, будет намного медленнее, но он может предложить что-то еще, что более точно находит (числовые) решения:

🔍 Видео

Методы решения систем нелинейных уравнений. Метод Ньютона. Численные методы. Лекция 14Скачать

Метод Ньютона | Лучший момент из фильма Двадцать одно 21Скачать

FreeDy010 Решение Системы нелинейных уравнений scipy sympyСкачать

МЗЭ 2021 Лекция 11 Метод Ньютона для решения систем нелинейных уравненийСкачать

15 Метод Ньютона (Метод касательных) Ручной счет Численные методы решения нелинейного уравненияСкачать

Решение нелинейных уравненийСкачать