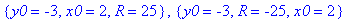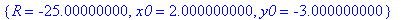Решение нелинейных систем уравнений maple (8 видео)

Содержание

Решение уравнений
Системы уравнений
Решение нелинейных уравнений средствами системы Maple
решение нелинейных уравнений.doc
Решение систем нелинейных уравнений
Пример:
📽️ Видео

Видео:После этого видео, ТЫ РЕШИШЬ ЛЮБУЮ Систему Нелинейных УравненийСкачать

Решение уравнений

Методы нахождения корней полиномов, решения уравнений, содержащих элементарные и специальные функции и систем сложных уравнений

Видео:Решение системы линейных уравнений в MapleСкачать

Системы уравнений

Maple может решать системы линейных и нелинейных уравнений, но это хитрое дело, поскольку, чтобы разобраться в происходящем, надо рисовать уравнения, а это сложнее, так как пространство решений – многомерное.

Применяются команды solve и fsolve , но в этом случае им задаются наборы (в фигурных скобках) уравнений и переменных.

В первом примере используем solve для простой задачи линейной алгебры: John вдвое старше Kimberly. Возраст Kimberly плюс возраст John равен 27. Найти возраст каждого. Если использовать пакет LinearAlgebra, то придется рассматривать матрицу, но можно применить solve (и fsolve ), которые могут непосредственно работать с уравнениями:

Поскольку не надо беспокоиться о переводе в матричный вид, то получился иной метод решения систем линейных уравнений.

solve и fsolve можно применять для решения нелинейных систем, т. е. систем уравнений, в которых переменные – квадраты, кубы, синусы, экспоненты и т. п. Например, вот система двух нелинейных уравнений:

Вначале попробуем применить команду solve :

Maple сделал по-умному: чтобы получить уравнение для х , он исключил у из Е2 с помощью Е1 . Затем он факторизовал это квадратное уравнение, выдал ответ (x,y)=(3,4) и свел оставшуюся часть задачи к кубической. Если завершить задачу командой evalf , получим:

Но если нарисовать кубическую часть в RootOf (для оценки положения корней), то увидите, что есть еще два решения. Где же они? Примените fsolve и получите:

что еще хуже, так как дает один корень. Для поиска корней можно задавать примерно правильные числа в качестве подсказок для fsolve :

Простой способ заставить Maple дать все 4 корня: повторяйте процедуру, заменяя все целые числа на числа с плавающей точкой:

Будьте изобретательны
и пробуйте разные пути решения задачи,
возможно, один сработает.

В Maple есть другой полезный инструмент для случая двух нелинейных уравнений с двумя неизвестными. Точно так же, как в задачах с одной переменной, полезно сначала строить график, чтобы увидеть, где есть решения. В данном случае двумерные графики помогут искать корни двух неизвестных величин. Примените команду построения графиков implicitplot , которая берет уравнение с двумя переменными, вроде x 2 – y = 5, и строит определяющую их кривую в плоскости xy (для добавления команды графики надо вначале загрузить пакет графики with(plots) ):

Для графического поиска решений постройте оба уравнения на одном графике и посмотрите, где две кривые пересекают друг друга.

Из картинки ясно, что две параболы пересекаются в четырех местах, поэтому должно быть четыре решения. Окно графика должно быть достаточным, чтобы увидеть всю картинку. А если оно мало, то получится вот что:

Если у вас есть три нелинейных уравнения с тремя переменными, implicitplot3d может сделать нечто подобное (см. Maple help).

Найдите все решения (Re и Im) системы уравнений

Чтобы определить количество искомых корней, сначала постройте график с помощью implicitplot .

Вот еще нелинейная система:

Вначале попробуем solve :

(Maple на мгновение задумается, но ничего не произойдет.) Теперь попробуем fsolve с диапазонами для каждой переменной:

Похоже, что (x, y, z) = (1, 1, 3) достаточно близко к решению. Предупреждение: в трех и более измерениях Maple может ошибиться и работать, несмотря на то, что:

(a) известно, что здесь есть решение и

(b) указано, где искать приближенное значение корня.

Для лучшего понимания, где следует искать решение, можно применить implicitplot3d :

Щелкните на рисунке и покрутите его, чтобы разглядеть подробнее. После этого перерисуйте график так, чтобы он был вблизи известного решения: [x, y, z]=[1, 1, 3]:

В середине графика все три поверхности – E1 , E2 и E3 – пересекаются в точке. Это и есть то, что искали с помощью implicitplot3d , но в целом рассматривать трехмерные задачи сложно.

Пусть гладкая функция y(x) представлена тремя точками (x 1 , y 1 ), (x 2 , y 2 ), (x 3 , y 3 ). Предположим, что эти точки определяют параболу вида y(x) = a + bx + cx 2 и что есть три аппроксимирующих уравнения для нахождения коэффициентов параболы a, b, c. Постройте эти три уравнения и используйте solve , чтобы найти формулы для a, b, c, а затем определите выражение Maple для параболы.

Задание выглядит вполне приемлемо для равноотстоящих точек. Пусть x 2 = x 1 + h и x 3 = x 1 + 2h . Упростим выражения для a, b, c. В результате получили приближенную форму функции, с которой можно работать:

(a) Оцените площадь под кривой между x 1 и x 3 путем интегрирования параболы между этими двумя пределами. Получится правило Симпсона. Чтобы посмотреть, хорош ли этот приближенный интеграл, задайте x 1 = 0, x 2 = 0.5, x 3 = 1.0 и y 1 = cos(x 1 ), y 2 = cos(x 2 ), y 3 = cos(x 3 ) , при этом приближенное значение площади будет близко к Дает ли формула приближенного интегрирования хороший результат?

(b) Оцените производную функции у(х) в средней точке х 2 путем дифференцирования параболы и вычисления значения производной в x = x 2 . Она называется формулой центральных разностей для первой производной. Проверьте ее точность при x 2 = 0.5, используя x 1 = 0.4 и x 3 = 0.6 с функцией

(c) Повторно дифференцируя формулу параболы, оцените вторую производную функции у(х) в x 2 . Это центральная вторая производная для равноотстоящих точек. Проверьте ее точность, как в части (b).

Эти формулы дифференцирования и интегрирования понадобятся в курсе физики.

Видео:Способы решения систем нелинейных уравнений. 9 класс.Скачать

Решение нелинейных уравнений средствами системы Maple

Автор работы: Пользователь скрыл имя, 31 Марта 2013 в 16:08, курсовая работа

Краткое описание

Системы компьютерной математики в образовании — они становятся не только удобным инструментальным средством для выполнения огромного числа учебных расчетов, но и средством предоставления учащимся, а нередко и педагогам, знаний в области математики, физики и иных наук, использующих математические методы. Это позволяет отнести такие системы к интеллектуальным компьютерным системам представления знаний и к экспертным системам в области математических расчетов. Трудно переоценить и их роль в подготовке высококачественных электронных уроков, учебных курсов и книг, имеющих великолепные (в том числе анимационные) средства визуализации вычислений и «живые» примеры, которые учащиеся могут перекраивать, как говорится, на свой «вкус и цвет».

Содержание

1 СПОСОБЫ ЗАДАНИЯ ФУНКЦИЙ……………………….. 5

2 ОСНОВНЫЕ ВОЖМОЖНОСТИ СИСТЕМЫ MAPLE

2.1 РЕШЕНИЕ УРАВНЕНИЙ………………………………………….. 8
2.2 РЕШЕНИЕ СИСТЕМ УРАВНЕНИЙ……………………………… 9

3 ЧИСЛЕННОЕ РЕШЕНИЕ НЕЛИНЕЙНЫХ УРАВНЕНИЙ

3.1 РЕШЕНИЕ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ………………… 10
3.2 РЕШЕНИЕ ТРАНСЦЕНДЕНТНЫХ
УРАВНЕНИЙ……………………………………………………. 12
3.3 РЕШЕНИЕ СИСТЕМ ТРАНСЦЕНДЕНТНЫХ
УРАВНЕНИЙ……………………………………………………… 15
3.4 РЕШЕНИЕ ФУНКЦИАНАЛЬНЫХ
УРАВНЕНИЙ……………………………………………………. 17

4 СИМВОЛЬНОЕ РЕШЕНИЕ НЕЛИНЕЙНЫХ УРАВНЕНИЙ

4.1 РЕШЕНИЕ ФУНКЦИАНАЛЬНЫХ И РЕКУРЕНТНЫХ
УРАВНЕНИЙ……………………………………………………… 18

СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ…………. 21

Прикрепленные файлы: 1 файл

Видео:Способы решения систем нелинейных уравнений. Практическая часть. 9 класс.Скачать

решение нелинейных уравнений.doc

1 СПОСОБЫ ЗАДАНИЯ ФУНКЦИЙ………………… …….. 5

2 ОСНОВНЫЕ ВОЖМОЖНОСТИ СИСТЕМЫ MAPLE

2.2 РЕШЕНИЕ СИСТЕМ УРАВНЕНИЙ……………………………… 9

3 ЧИСЛЕННОЕ РЕШЕНИЕ НЕЛИНЕЙНЫХ УРАВНЕНИЙ

3.1 РЕШЕНИЕ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ………………… 10

3.2 РЕШЕНИЕ ТРАНСЦЕНДЕНТНЫХ

3.3 РЕШЕНИЕ СИСТЕМ ТРАНСЦЕНДЕНТНЫХ

3.4 РЕШЕНИЕ ФУНКЦИАНАЛЬНЫХ

4 СИМВОЛЬНОЕ РЕШЕНИЕ НЕЛИНЕЙНЫХ УРАВНЕНИЙ

4.1 РЕШЕНИЕ ФУНКЦИАНАЛЬНЫХ И РЕКУРЕНТНЫХ

СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ…………. 21

Системы компьютерной математики (СКМ) класса Maple были созданы корпорацией Waterloo Maple, Inc. (Канада) как системы компьютерной алгебры с расширенными возможностями в области символьных (аналитических) вычислений. Новейшая версия Maple 8 позиционируется как универсальная система компьютерной математики, рассчитанная на широкого пользователя. Система содержит средства для выполнения быстрых численных расчетов, лежащих в основе математического моделирования различных явлений окружающего нас мира, систем и устройств различного назначения.

Цель данной курсовой работы – изучение литературы по теме “Решение нелинейных уравнений средствами системы Maple” и изучение области применения.

В качестве задачи поставленной передо мной руководителем, является решение нелинейных уравнений средствами системы Maple.

Заслуженной популярностью системы Maple (всех версий) пользуются в системах образования многих стран мира. Свыше 300 самых крупных университетов мира (включая и наш МГУ) взяли эту систему на вооружение и используют ее в научных и учебных расчетах. А число только зарегистрированных пользователей системы уже давно превысило миллион.

Maple — типичная интегрированная система. Она объединяет в себе:

мощный язык программирования (он же язык для интерактивного общения с системой);
редактор для подготовки и редактирования документов и программ;
современный многооконный пользовательский интерфейс с возможностью работы в диалоговом режиме;
мощную справочную систему со многими тысячами примеров;
ядро алгоритмов и правил преобразования математических выражений;
численный и символьный процессоры;
систему диагностики;
библиотеки встроенных и дополнительных функций;
пакеты функций сторонних производителей и поддержку некоторых других языков программирования и программ.

Ко всем этим средствам имеется полный доступ прямо из окна программы. Система Maple прошла долгий путь развития и апробации. Она реализована на больших ЭВМ, рабочих станциях Sun, ПК, работающих с операционной системой Unix, ПК класса IBM PC, Macintosh и др. Все это самым положительным образом повлияло на ее отработку и надежность (в смысле высокой вероятности правильности решений и отсутствия сбоев в работе). Не случайно ядро системы Maple используется целым рядом других мощных систем компьютерной математики, например системами класса Mathcad и MATLAB.

1 СПОСОБЫ ЗАДАНИЯ ФУНКЦИЙ

В системе Maple имеется несколько способов представления функции.

Способ 1.Определение функции с помощью оператора присваивания (:=): какому-то выражению присваивается имя, например:

Если задать конкретное значение х ,то получится значение функции f для этого х .Например, если продолжить предыдущий пример и вычислить значение f при х= /4,то следует записать:

После выполнения этих команд переменная x имеет заданное конкретное значение /4.

Чтобы насовсем не присваивать переменной конкретного значения, удобнее использовать команду подстановки subs(,f), где в фигурных скобках указываются переменные хi и их новые значения аi (i=1,2,…), которые следует подставить в функцию f . Например:

Все вычисления в Maple по умолчанию производятся символьно, то есть результат будет содержать в явном виде иррациональные константы, такие как, е,p и другие. Чтобы получить приближенное значение в виде числа с плавающей запятой, следует использовать команду evalf (expr,t), где expr –выражение в числах после запятой. Например, в продолжение предыдущего примера, вычислим полученное значение функции приближенно:

Здесь использован символ (%) для вызова предыдущей команды.

Так же имеется возможность переходить в функции к полярным координатам, после ее определения.

Способ 2. Определение функции с помощью функционального оператора, который ставит в соответствие набору переменных (x1,x2,…) одно или несколько выражений (f1,f2,…). Например, определение функции двух переменных с помощью функционального оператора выглядит следующим образом:

_{Обращение к этой функции осуществляется наиболее привычным способом, когда в скобках вместо аргументов функции указываются конкретные значения переменных. В продолжение предыдущего приме}_{ра вычисляется значение функции:}

_{Способ 3.С помощью команды unapply (expr,x1,x2,…),где expr- выражение, x1,x2,…-набор переменных, от которых оно зависит, можно преобразовать выражение expr в функциональный оператор. Например:}

_В _{Maple имеется возможность определения неэлементарных функций вида посредством команды} _{piecewise(cond_1,f1, cond_2,f2,…)} _.

_{Например, функция} _{записывается следующим образом:}

А функция f(x)= записывается так:

2 ОСНОВНЫЕ ВОЗМОЖНОСТИ СИСТЕМЫ MAPLE ПРИ РЕШЕНИИ НЕЛИНЕЙНЫХ УРАВНЕНИЙ

_Maple _{–это пакет для аналитических вычислений на компьютере, содержащий более двух тысяч команд, которые позволяют решать задачи алгебры, геометрии, математического анализа, дифференциальных уравнений, статистики, математической физики. Работа в Maple проходит в режиме сессии- пользователь вводит предложения (команды, выражения, процедуры), которые воспринимаются условно и обрабатываются Maple.}

_{2.1 Решение уравнений}

Для решения уравнений в Maple существует универсальная команда solve( eq,x),где eg — уравнение, х – переменная, относительно которой уравнение надо разрешить. В результате выполнения этой команды в строке вывода появиться выражение, которое является решением данного уравнения. Например :

Если уравнение имеет несколько решений, которые могут понадобятся для дальнейших расчетов, то команде solve следует присвоить какое-нибудь имя name.Обращение к какому-либо k-ому решению данного уравнения производится указанием его имени name с номером решения k в квадратных скобках:name[k].Например:

2.2 Решение систем уравнений

Cистемы уравнений решаются с помощью такой же команды solve(,), только теперь в параметрах команды следует указать в первых фигурных скобках через запятую уравнения ,а во вторых фигурных скобках перечисляются через запятую переменные , относительно которых требуется решить систему. Если будет необходимо для дальнейших вычислений использовать полученные решения уравнений, то команде solve следует присвоить какое-нибудь имя name.Затем выполняется команда присвоения assign(name).После этого над решениями можно будет производить математические операции. Например, решим следующую систему:

_{Приведем еще один пример решения системы уравнений. содержащей три переменные:}

_{Найдем сумму полученных решений:}

_{3 ЧИ}_{СЛЕННОЕ РЕШЕНИЕ НЕЛИНЕЙНЫХ УРАВНЕНИЙ}

_{Нелинейное уравнение в общем виде записывается следующим образом:} _{F(X) = 0.} _{Нелинейные уравнения могут быть двух видов:}

_{1.Алгебраические:} _{anx n +an-1x n-1 +…+a0=0}

_{2.Трансцендентные – это уравнения, в которых} _{x является аргументом тригонометрической, логарифмической или показательной функции.}

_{Значение} _{x0, при котором существует равенство f(x0)=0 называется} _корнем _{уравнения. Решить уравнение – значит найти этот корень.}

_{3.1 Решение алгебраических уравнений}

_{Для численного реш}_{ения уравнений используется специальная команда} _{fsolve ( eg ,x ),} _{где eg-уравнение, а x-переменная, относительно которой это уравнение надо разрешить.}

_{Рассмотрим такой пример: численно решить уравнение} _{23x 5 +105x 4 -10x 2 +17x=0} _{на отрезке [-1;1].}

fsolve( poly, x, -1..1 );

_{Решим еще одно уравнение, найдя его корни на отрезках [1;2] и [4;8] .}

_{Так же можно найти решение этого уравнения на множестве комплексных чисел, используя дополнительный параметр} _complex:

> fsolve(q, x, complex);

_{3.1 Решение алгебраических уравне}_ний

_{Для численного решения уравнений используется специальная команда} _{fsolve ( eg ,x ),} _{где eg-уравнение, а x-переменная, относительно которой это уравнение надо разрешить.}

_{Рассмотрим такой пример: численно решить уравнение} _{23x 5 +105x 4 -10x 2 +17x=0} _{на отрезке [-1;1].}

_{Заранее присвоим нашему уравнению имя} _poly _:

fsolve( poly, x, -1..1 );

_{Решим еще одно уравнение, найдя его корни на отрезках [1;2] и [4;8] .}

> fsolve(q, x, complex);

₃_{.2 Решение трансцендентных уравнений.}

Для решения данной группы уравнений применяется универсальная команда fsolve.При решении уравнений можно осуществлять упрощение выражений посредством команды simplify(eg).

Приведение подобных членов в выражении осуществляется командой collect(exp,var), где exp – выражение, var – имя переменной, относительно которой следует собирать подобные. В команде simplify в качестве параметров можно указать, какие выражения преобразовывать. Например, при указании simplify(eq,trig) будет производиться упрощение при использовании большого числа тригонометрических соотношений.

С помощью команды convert(exp, param), где exp – выражение, которое будет преобразовано в указанный тип param. В частности, можно преобразовать выражение, содержащее sinx и cosx, в выражение, содержащее только tgx, если указать в качестве параметра tan, или, наоборот, tgx, ctgx можно перевести в sinx и сosx, если в параметрах указать sincos.

Видео:Алгоритмы С#. Метод Ньютона для решения систем уравненийСкачать

Решение систем нелинейных уравнений

Для решения уравнений и систем в Maple предназначены функции solve и fsolve. Напомним, что solve ищет решение в аналитической форме, a fsolve — в численной. Синтаксис этих команд при решении систем уравнений следующий :
solve(, );
fsolve (, , ).

То есть обе команды решают систему уравнений, заданную первым параметром, относительно переменных, указанных во втором. Важной особенностью синтаксиса этих функций является то, что система уравнений и ее неизвестные задаются в виде множества. Кроме того, если не задано множество переменных, относительно которых следует разрешить уравнение, Maple выдаст все решения относительно всех неопределенных переменных. Если же уравнения системы заданы не в виде равенства, а в виде выражения, то это выражение воспринимается пакетом как левая часть уравнения с нулевой правой частью.

Видео:МЗЭ 2021 Лекция 11 Метод Ньютона для решения систем нелинейных уравненийСкачать

Пример:

Здесь показано решение системы с помощью функции solve. Как видим, она предлагает два аналитических решения. Но одно из них не удовлетворяет условию задачи, так как радиус окружности не может быть отрицательным. Чтобы выделить из множества верное решение, можно применить функцию eval.
u1:=(26-x0)^2+(4-y0)^2-R^2:
u2:=(9-x0)^2+(21-y0)^2-R^2:
u3:=(17-x0)^2+(17-y0)^2-R^2:
solve(,);

S:=solve(,):
eval(S[1]);

Этот пример содержит решение задачи с применением функции fsolve. В первом случае пользователю предлагается лишь отрицательное решение, не корректное с точки зрения поставленной задачи. Во втором случае получаем верное решение, установив в опциях положительный диапазон изменения радиуса.
fsolve(,);

fsolve(,,);