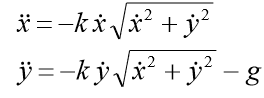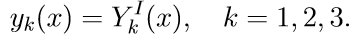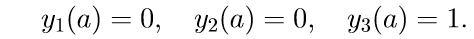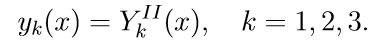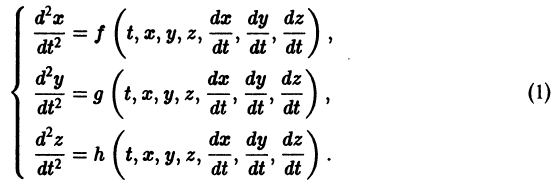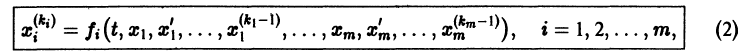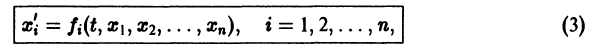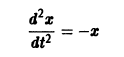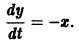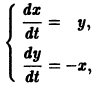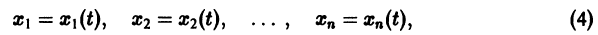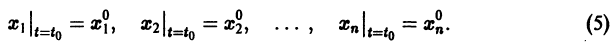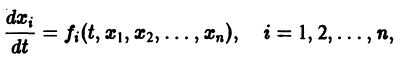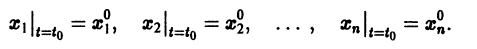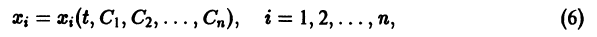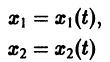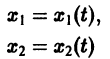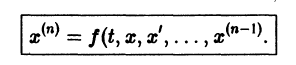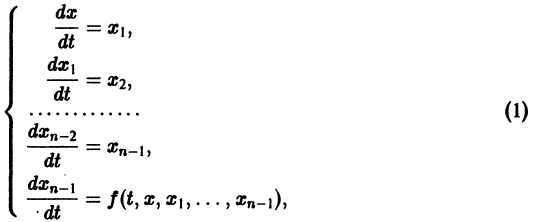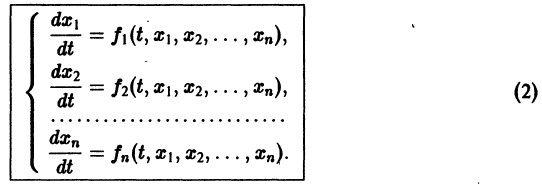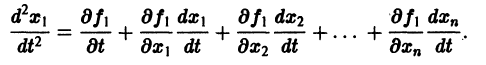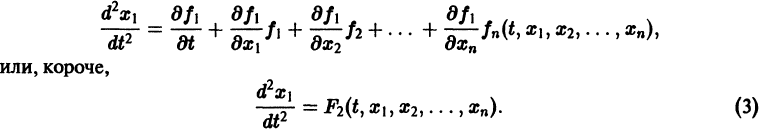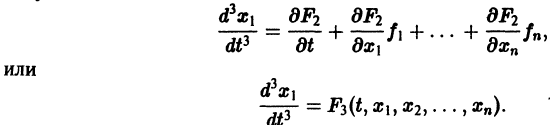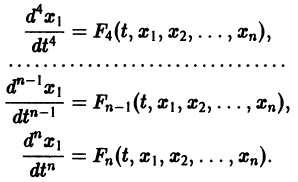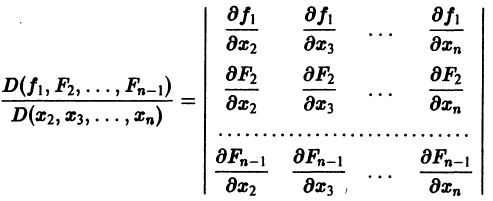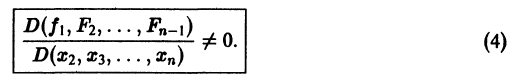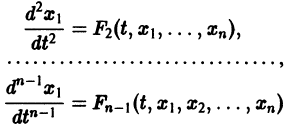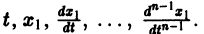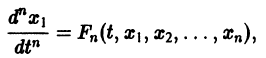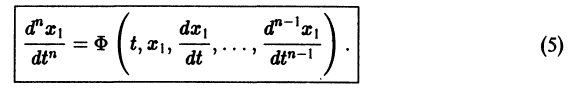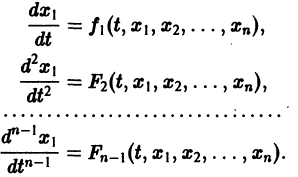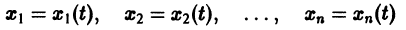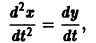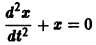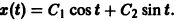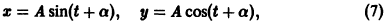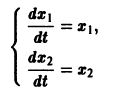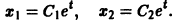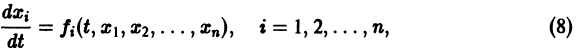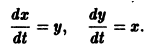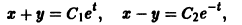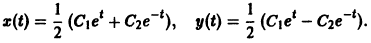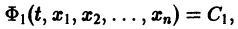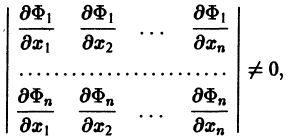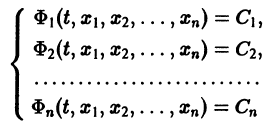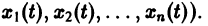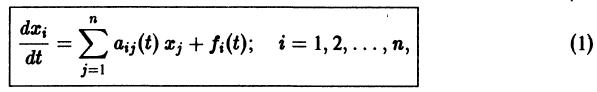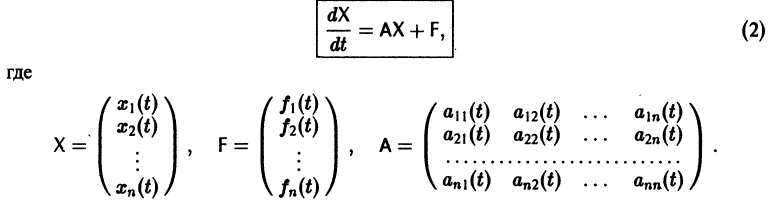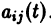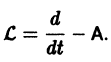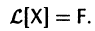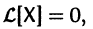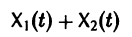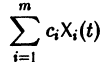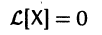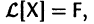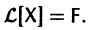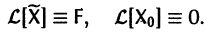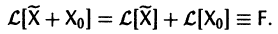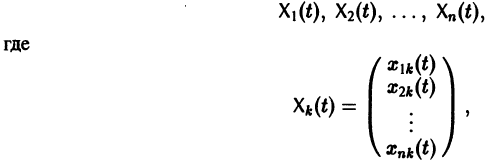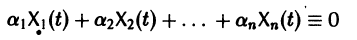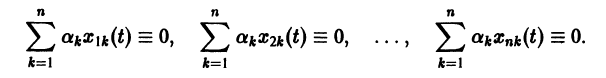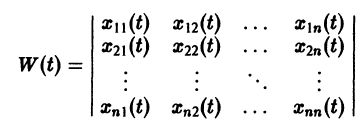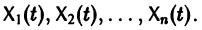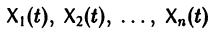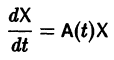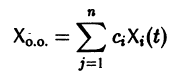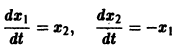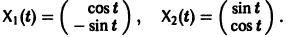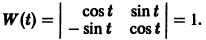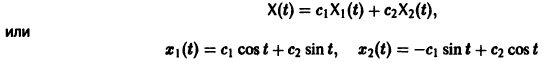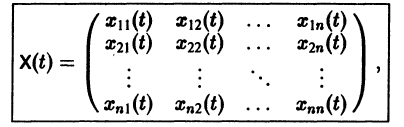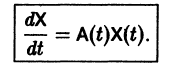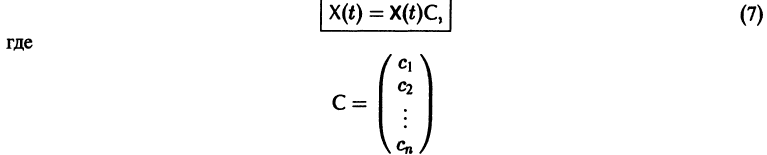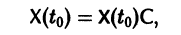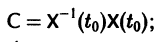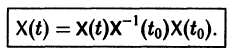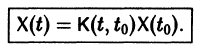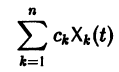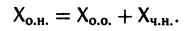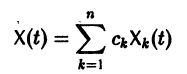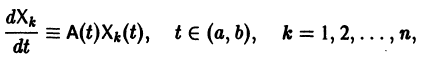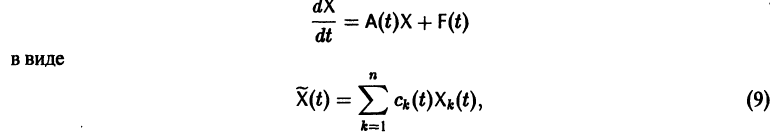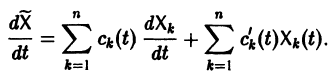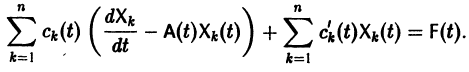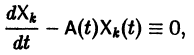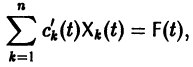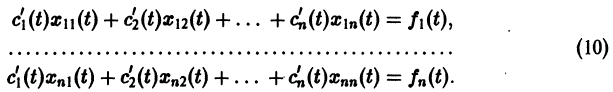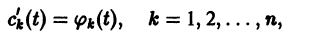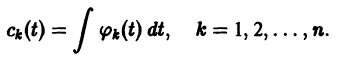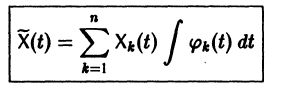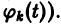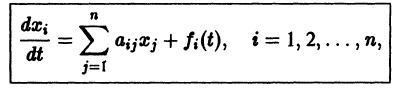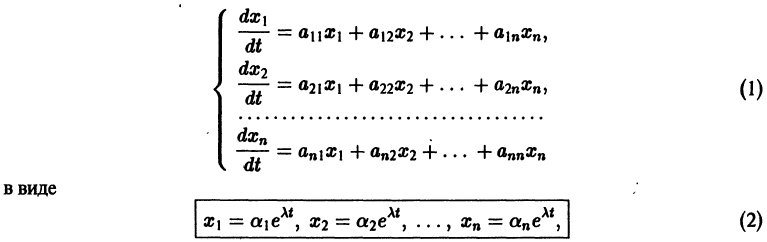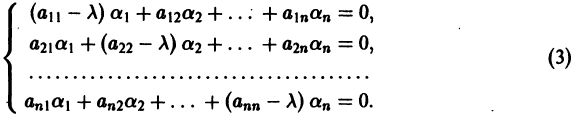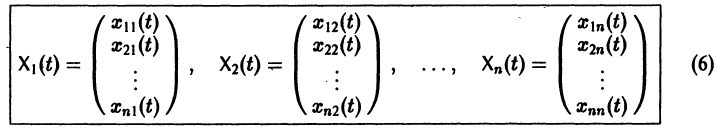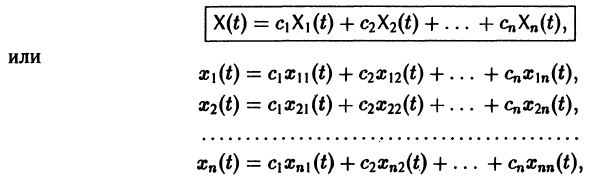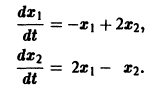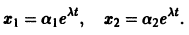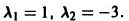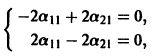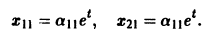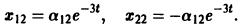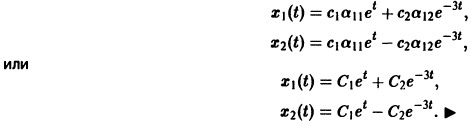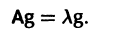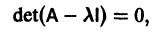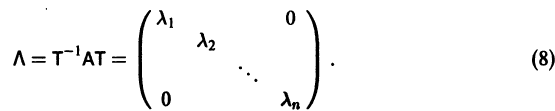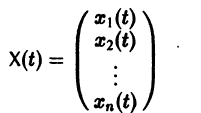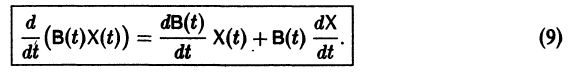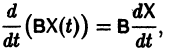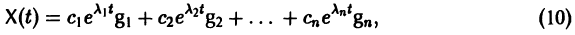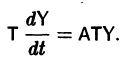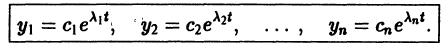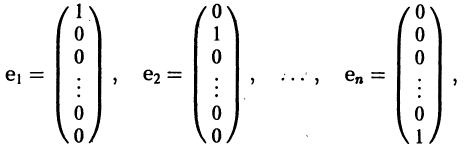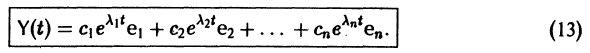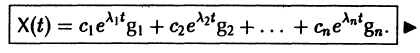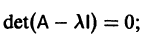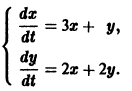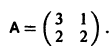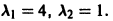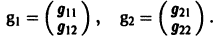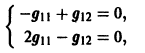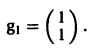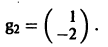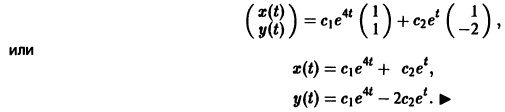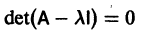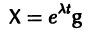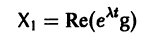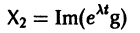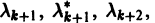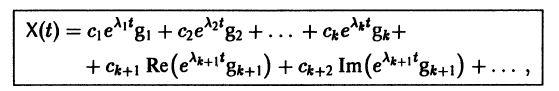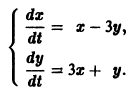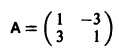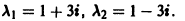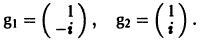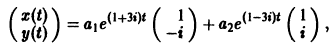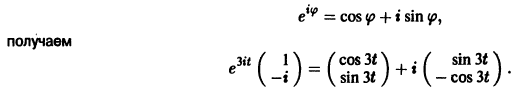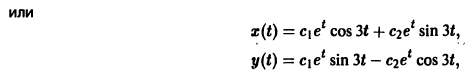- Введение:
- Краткие теоретические и фактические данные по рассматриваемым методам и программным средствам для численного решения СДУ
- Вычислительный эксперимент по определению абсолютной погрешности численного решения нелинейного дифференциального уравнения с использованием обеих функций def odein(),def oden() модуля scipy.integrate и адаптированного к Python методов Рунге—Кутта и Рунге—Кутта— Фельберга
- Численный эксперимент по сравнению быстродействия численного решения СДУ при использовании функции ode с атрибутом dopri5 (метод Рунге – Кутты 5 порядка) и с использованием адаптированного к Python метода Рунге—Кутта— Фельберга
- Решение краевой задачи с поточно разделёнными краевыми условиями
- Вывод
- Системы дифференциальных уравнений с примерами решения и образцами выполнения
- Решение систем дифференциальных уравнений
- Методы интегрирования систем дифференциальных уравнений
- Метод исключения
- Метод интегрируемых комбинаций
- Системы линейных дифференциальных уравнений
- Фундаментальная матрица
- Квадратная матрица
- Метод вариации постоянных
- Системы линейных дифференциальных уравнений с постоянными коэффициентами
- Метод Эйлера
- Матричный метод
- Понятие о системах дифференциальных уравнений
- 📹 Видео
Введение:
При математическом моделировании ряда технических устройств используются системы дифференциальных нелинейных уравнений. Такие модели используются не только в технике, они находят применение в экономике, химии, биологии, медицине, управлении.
Исследование функционирования таких устройств требуют решения указанных систем уравнений. Поскольку основная часть таких уравнений являются нелинейными и нестационарными, часто невозможно получить их аналитическое решение.
Возникает необходимость использовать численные методы, наиболее известным из которых является метод Рунге — Кутты [1]. Что касается Python, то в публикациях по численным методам, например [2,3], данных по применение Рунге — Кутты крайне мало, а по его модификации — методу Рунге-Кутта-Фельберга вообще нет.
В настоящее время, благодаря простому интерфейсу, наибольшее распространение в Python имеет функцию odeint из модуля scipy.integrate. Вторая функция ode из этого модуля реализует несколько методов, в том числе и упомянутый пятиранговый метод Рунге-Кутта-Фельберга, но, вследствие универсальности, имеет ограниченное быстродействие.
Целью настоящей публикации является сравнительный анализ перечисленных средств численного решения систем дифференциальных уравнений с модифицированным автором под Python методом Рунге-Кутта-Фельберга. В публикации так же приведены решения по краевым задачам для систем дифференциальных уравнений (СДУ).
Краткие теоретические и фактические данные по рассматриваемым методам и программным средствам для численного решения СДУ
Для одного дифференциального уравнения n – го порядка, задача Коши состоит в нахождении функции, удовлетворяющей равенству:
и начальным условиям
Перед решением эта задача должна быть переписана в виде следующей СДУ
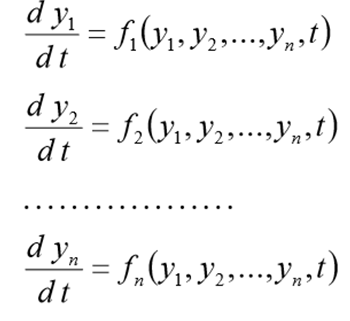
с начальными условиями
Модуль имеет две функции ode() и odeint(), предназначенные для решения систем обыкновенных дифференциальных уравнений (ОДУ) первого порядка с начальными условиями в одной точке (задача Коши). Функция ode() более универсальная, а функция odeint() (ODE integrator) имеет более простой интерфейс и хорошо решает большинство задач.
Функция odeint() имеет три обязательных аргумента и много опций. Она имеет следующий формат odeint(func, y0, t[,args=(), . ]) Аргумент func – это имя Python функции двух переменных, первой из которых является список y=[y1,y2. yn], а второй – имя независимой переменной.
Функция func должна возвращать список из n значений функций 
Второй аргумент y0 функции odeint() является массивом (или списком) начальных значений 
Третий аргумент является массивом моментов времени, в которые вы хотите получить решение задачи. При этом первый элемент этого массива рассматривается как t0.
Функция odeint() возвращает массив размера len(t) x len(y0). Функция odeint() имеет много опций, управляющих ее работой. Опции rtol (относительная погрешность) и atol (абсолютная погрешность) определяют погрешность вычислений ei для каждого значения yi по формуле
Они могут быть векторами или скалярами. По умолчанию
Вторая функция модуля scipy.integrate, которая предназначена для решения дифференциальных уравнений и систем, называется ode(). Она создает объект ОДУ (тип scipy.integrate._ode.ode). Имея ссылку на такой объект, для решения дифференциальных уравнений следует использовать его методы. Аналогично функции odeint(), функция ode(func) предполагает приведение задачи к системе дифференциальных уравнений вида (1) и использовании ее функции правых частей.
Отличие только в том, что функция правых частей func(t,y) первым аргументом принимает независимую переменную, а вторым – список значений искомых функций. Например, следующая последовательность инструкций создает объект ODE, представляющий задачу Коши.
При построении численных алгоритмов будем считать, что решение этой дифференциальной задачи существует, оно единственно и обладает необходимыми свойствами гладкости.
При численном решении задачи Коши
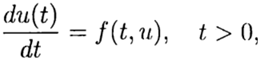

по известному решению в точке t =0 необходимо найти из уравнения (3) решение при других t. При численном решении задачи (2),(3) будем использовать равномерную, для простоты, сетку по переменной t с шагом т > 0.
Приближенное решение задачи (2), (3) в точке 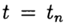

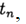


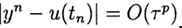

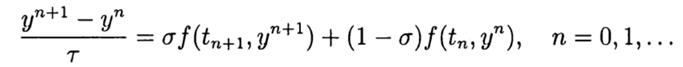
При 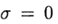
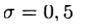
Явные схемы второго и более высокого порядка аппроксимации удобно строить, ориентируясь на метод предиктор-корректор. На этапе предиктора (предсказания) используется явная схема
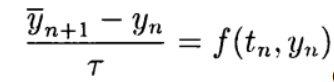
а на этапе корректора (уточнения) — схема
В одношаговых методах Рунге—Кутта идеи предиктора-корректора реализуются наиболее полно. Этот метод записывается в общем виде:

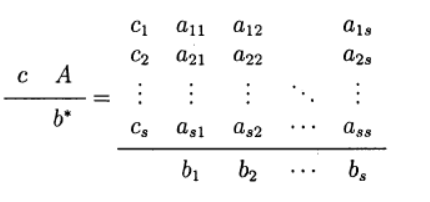
Формула (6) основана на s вычислениях функции f и называется s-стадийной. Если 
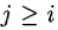

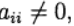

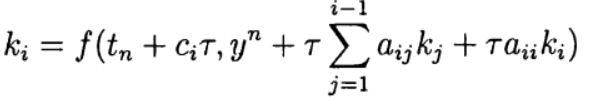
О таком методе Рунге—Кутта говорят как о диагонально-неявном. Параметры 
Одним из наиболее распространенных является явный метод Рунге—Кутта четвертого порядка

Метод Рунге—Кутта— Фельберга
Привожу значение расчётных коэффициентов 
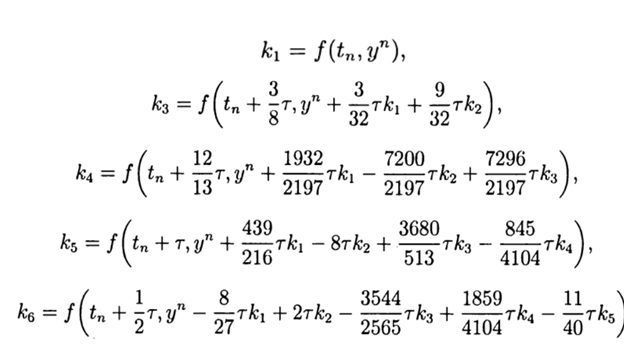
С учётом(9) общее решение имеет вид:
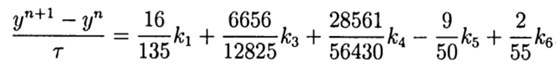
Это решение обеспечивает пятый порядок точности, остаётся его адаптировать к Python.
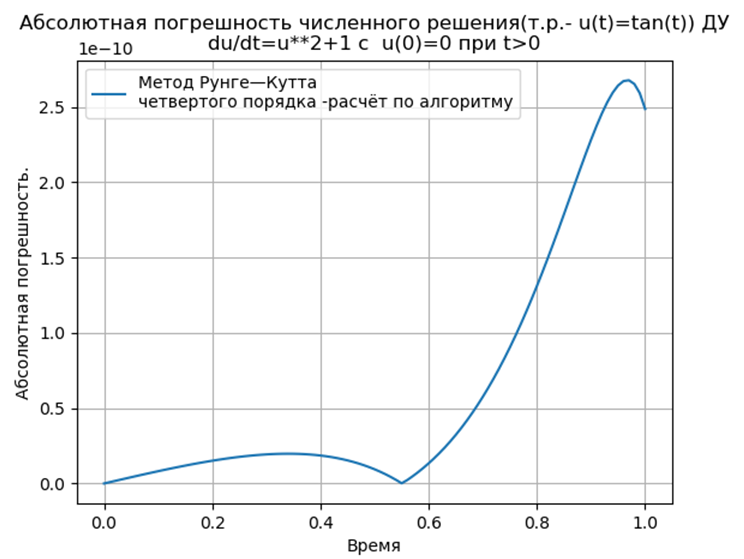
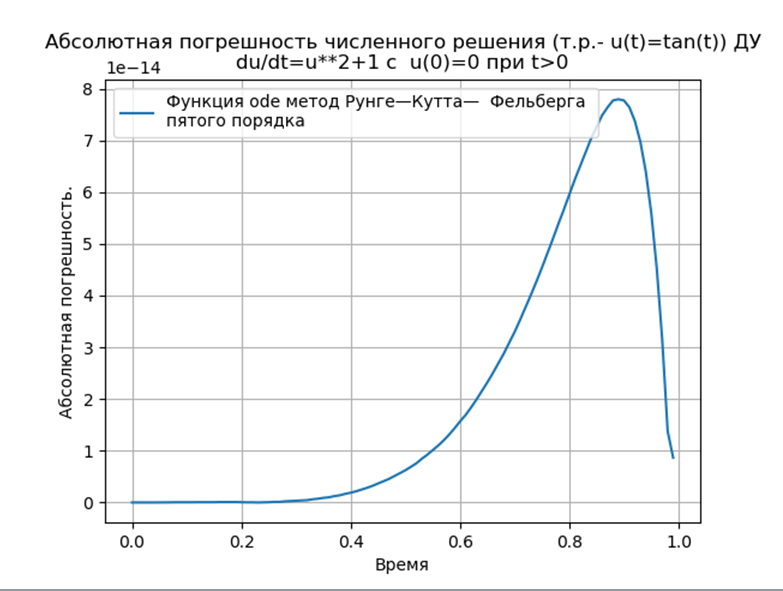
Вычислительный эксперимент по определению абсолютной погрешности численного решения нелинейного дифференциального уравнения  с использованием обеих функций def odein(),def oden() модуля scipy.integrate и адаптированного к Python методов Рунге—Кутта и Рунге—Кутта— Фельберга
с использованием обеих функций def odein(),def oden() модуля scipy.integrate и адаптированного к Python методов Рунге—Кутта и Рунге—Кутта— Фельберга
Адаптированные к Python методы Рунге—Кутта и Рунге—Кутта— Фельберга имеют меньшую абсолютную, чем решение с применением функции odeint, но большую, чем с использованием функции edu. Необходимо провести исследование быстродействия.
Численный эксперимент по сравнению быстродействия численного решения СДУ при использовании функции ode с атрибутом dopri5 (метод Рунге – Кутты 5 порядка) и с использованием адаптированного к Python метода Рунге—Кутта— Фельберга
Сравнительный анализ проведём на примере модельной задачи, приведенной в [2]. Чтобы не повторять источник, приведу постановку и решение модельной задачи из [2].
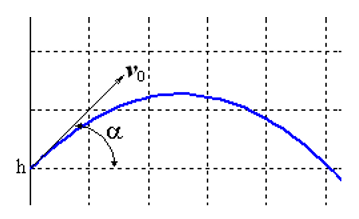
Решим задачу Коши, описывающую движение тела, брошенного с начальной скоростью v0 под углом α к горизонту в предположении, что сопротивление воздуха пропорционально квадрату скорости. В векторной форме уравнение движения имеет вид
где 



Особенность этой задачи состоит в том, что движение заканчивается в заранее неизвестный момент времени, когда тело падает на землю. Если обозначить 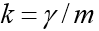
К системе следует добавить начальные условия: 

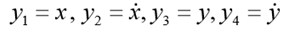
Для модельной задачи положим 
Flight time = 1.2316 Distance = 5.9829 Height =1.8542
Flight time = 1.1016 Distance = 4.3830 Height =1.5088
Flight time = 1.0197 Distance = 3.5265 Height =1.2912
Flight time = 0.9068 Distance = 2.5842 Height =1.0240
Время на модельную задачу: 0.454787
Для реализации средствами Python численного решения СДУ без использования специальных модулей, мною была предложена и исследована следующая функция:
def increment(f, t, y, tau
k1=tau*f(t,y)
k2=tau*f(t+(1/4)*tau,y+(1/4)*k1)
k3 =tau *f(t+(3/8)*tau,y+(3/32)*k1+(9/32)*k2)
k4=tau*f(t+(12/13)*tau,y+(1932/2197)*k1-(7200/2197)*k2+(7296/2197)*k3)
k5=tau*f(t+tau,y+(439/216)*k1-8*k2+(3680/513)*k3 -(845/4104)*k4)
k6=tau*f(t+(1/2)*tau,y-(8/27)*k1+2*k2-(3544/2565)*k3 +(1859/4104)*k4-(11/40)*k5)
return (16/135)*k1+(6656/12825)*k3+(28561/56430)*k4-(9/50)*k5+(2/55)*k6
Функция increment(f, t, y, tau) обеспечивает пятый порядок численного метода решения. Остальные особенности программы можно посмотреть в следующем листинге:
Время на модельную задачу: 0.259927
Предложенная программная реализация модельной задачи без использования специальных модулей имеет почти в двое большее быстродействие, чем с функцией ode, однако нельзя забывать, что ode имеет более высокую точность численного решения и возможности выбора метода решения.
Решение краевой задачи с поточно разделёнными краевыми условиями
Приведем пример некоторой конкретной краевой задачи с поточно разделенными краевыми условиями:
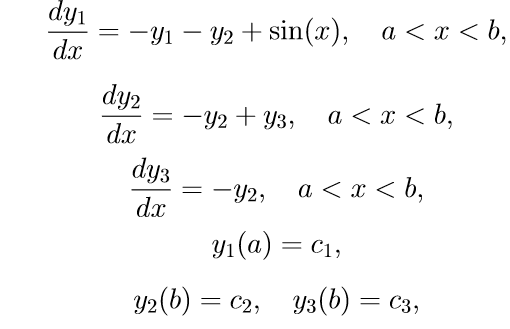
Для решения задачи (11) используем следующий алгоритм:
1. Решаем первые три неоднородные уравнения системы (11) с начальными условиями 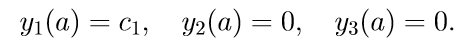
Введем обозначение для решения задачи Коши:
2. Решаем первые три однородные уравнения системы (11) с начальными условиями 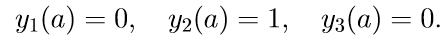
Введем обозначение для решения задачи Коши:
3. Решаем первые три однородные уравнения системы (11) с начальными условиями
Введем обозначение для решения задачи Коши:
4. Общее решение краевой задачи (11) при помощи решений задач Коши записывается в виде линейной комбинации решений: 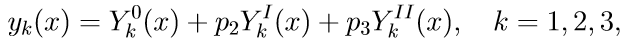
где p2, p3 — некоторые неизвестные параметры.
5. Для определения параметров p2, p3, используем краевые условия последних двух уравнений (11), то есть условия при x = b. Подставляя, получим систему линейных уравнений относительно неизвестных p2, p3:

Решая (12), получим соотношения для p2, p3.
По приведенному алгоритму с применением метода Рунге—Кутта—Фельберга получим следующую программу:
y0[0]= 0.0
y1[0]= 1.0
y2[0]= 0.7156448588231397
y3[0]= 1.324566562303714
y0[N-1]= 0.9900000000000007
y1[N-1]= 0.1747719838716767
y2[N-1]= 0.8
y3[N-1]= 0.5000000000000001
Время на модельную задачу: 0.070878
Вывод
Разработанная мною программа отличается от приведенной в [3] меньшей погрешностью, что подтверждает приведенный в начале статьи сравнительный анализ функции odeint с реализованным на Python метода Рунге—Кутта—Фельберга.
3. Н.М. Полякова, Е.В. Ширяева Python 3. Создание графического интерфейса пользователя (на примере решения методом пристрелки краевой задачи для линейных обыкновенных дифференциальных уравнений). Ростов-на-Дону 2017.
Видео:Решение системы дифференциальных уравнений методом ЭйлераСкачать

Системы дифференциальных уравнений с примерами решения и образцами выполнения
Также как и обыкновенные дифференциальные уравнения, системы дифференциальных уравнений применяются для описания многих процессов реальной действительности. В частности, к ним относятся различного рода физические и химические процессы, процессы нефте- и газодобычи, геологии, экономики и т.д. Действительно, если некоторые физические величины (перемещение тела, пластовое давление жидкости в фиксированной точке с тремя координатами, концентрация веществ, объемы продаж продуктов) оказываются меняющимися со временем под воздействием тех или иных факторов, то, как правило, закон их изменения по времени описывается именно системой дифференциальных уравнений, т.е. системой, связывающей исходные переменные как функции времени и производные этих функций. Независимой переменной в системе дифференциальных уравнений может выступать не только время, но и другие физические величины: координата, цена продукта и т.д.
Видео:Решение нелинейных системСкачать

Решение систем дифференциальных уравнений
К системе дифференциальных уравнений приводит уже простейшая задача динамики точки: даны силы, действующие на материальную точку; найти закон движения, т. е. найти функции 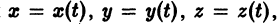
Здесь x, у, z — координаты движущейся точки, t — время, f, g, h — известные функции своих аргументов.
Система вида (1) называется канонической. Обращаясь к общему случаю системы т дифференциальных уравнений с т неизвестными функциями 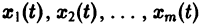
разрешенную относительно старших производных. Система уравнений первого порядка, разрешенных относительно производных от искомых функций,
Если 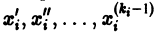
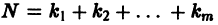
Например, одно уравнение
является мастным случаем канонической системы. Положив 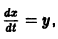
В результате получаем нормальную систему уравнений
эквивалентную исходному уравнению.
Определение:
Решением нормальной системы (3) на интервале (а, Ь) изменения аргумента t называется всякая система n функций
дифференцируемых на интервале а
Теорема:
Существования и единственности решения задачи Коши. Пусть имеем нормальную систему дифференциальных уравнений
и пусть функции 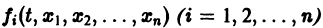
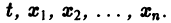
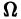
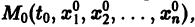

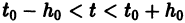
Определение:
Система n функций
зависящих от t и n произвольных постоянных 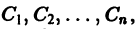
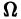
1) при любых допустимых значениях 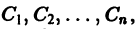
2) в области 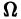
Решения, получающиеся из общего при конкретных значениях постоянных 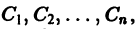
Обратимся для наглядности к нормальной системе двух уравнений,
Будем рассматривать систему значений t, x1, х2 как прямоугольные декартовы координаты точки трехмерного пространства, отнесенного к системе координат 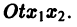
системы (7), принимающее при 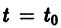
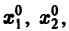
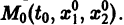
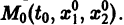
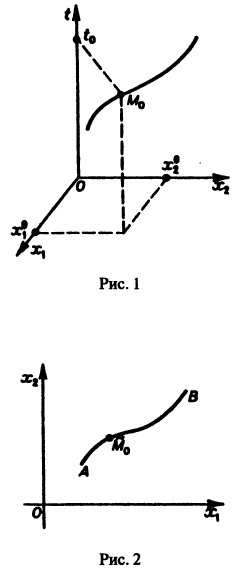
Нормальной системе (7) и ее решению можно придать еще такое истолкование: будем независимую переменную t рассматривать как параметр, а решение
системы — как параметрические уравнения кривой на плоскости 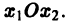
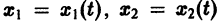
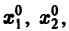
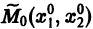
Методы интегрирования систем дифференциальных уравнений
Метод исключения
Один из методов интегрирования — метод исключения. Частным случаем канонической системы является одно уравнение n-го порядка, разрешенное относительно старшей производной
Введя новые функции 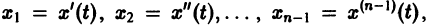
т. е. одно уравнение n-го порядка эквивалентно нормальной системе (1)
Можно утверждать и обратное, что, вообще говоря, нормальная система п уравнений первого порядка эквивалентна одному уравнению порядка n. На этом и основан метод исключения для интегрирования систем дифференциальных уравнений.
Делается это так. Пусть имеем нормальную систему
Продифференцируем первое из уравнений (2) по t. Имеем
Заменяя в правой части производные 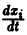
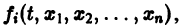
Уравнение (3) снова дифференцируем по t. Принимая во внимание систему (2), получим
Продолжая этот процесс, найдем
Предположим, что определитель
(якобиан системы функций 
Тогда система уравнений, составленная из первого уравнения системы (2) и уравнений
будет разрешима относительно неизвестных 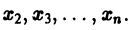
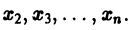
Внося найденные выражения в уравнение
получим одно уравнение n-го порядка
Из самого способа его построения следует, что если 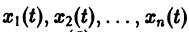
Обратно, пусть Х1(t) — решение уравнения (5). Дифференцируя это решение по t, вычислим 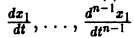
от t в систему уравнений
По предположению эту систему можно разрешить относительно 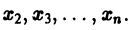

Можно показать, что так построенная система функций
составляет решение системы дифференциальных уравнений (2). Пример:
Требуется проинтегрировать систему
Дифференцируя первое уравнение системы, имеем
откуда, используя второе уравнение, получаем
— линейное дифференциальное уравнение второго порядка с постоянными коэффициентами с одной неизвестной функцией. Его общее решение имеет вид
В силу первого уравнения системы находим функцию
Найденные функции x(t), y(t), как легко проверить, при любых значениях С1 и С2 удовлетворяют заданной системе.
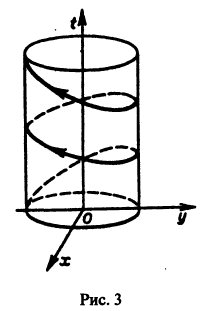
Функции x(t), y(t) можно представить в виде
откуда видно, что интегральные кривые системы (6) — винтовые линии с шагом 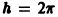
Исключая в формулах (7) параметр t, получаем уравнение
так что фазовые траектории данной системы суть окружности с центром в начале координат — проекции винтовых линий на плоскость хОу.
При А = 0 фазовая траектория состоит из одной точки х = 0, у = 0, называемой точкой покоя системы.
Замечание:
Может оказаться, что функции 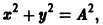
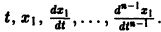
нельзя заменить эквивалентным уравнением второго порядка относительно х1 или x2. Эта система составлена из пары уравнений 1-го порядка, каждое из которых интегрируется независимо, что дает
Метод интегрируемых комбинаций
Интегрирование нормальных систем дифференциальных уравнений
иногда осуществляется методом интегрируемых комбинаций.
Интегрируемой комбинацией называется дифференциальное уравнение, являющееся следствием уравнений (8), но уже легко интегрирующееся.
Пример:
Складывая почленно данные уравнения, находим одну интегрируемую комбинацию:
Вычитая почленно из первого уравнения системы второе, получаем вторую интегрируемую комбинацию:
Мы нашли два конечных уравнения
из которых легко определяется общее решение системы:
Одна интегрируемая комбинация дает возможность получить одно уравнение
связывающее независимую переменную t и неизвестные функции 
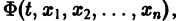
Если найдено п первых интегралов системы (8) и все они независимы, т. е. якобиан системы функций 
то задача интефирования системы (8) решена (так как из системы
определяются все неизвестные функции
Системы линейных дифференциальных уравнений
Система дифференциальных уравнений называется линейной, если она линейна относительно неизвестных функций и их производных, входящих в уравнение. Система n линейных уравнений первого порядка, записанная в нормальной форме, имеет вид
или, в матричной форме,
Теорема:
Если все функции 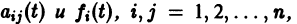
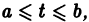
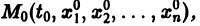
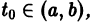
Действительно, в таком случае правые части системы (1) непрерывны по совокупности аргументов t, 
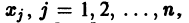
Введем линейный оператор
Тогда система (2) запишется в виде
Если матрица F — нулевая, т. е. 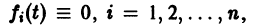
Приведем некоторые теоремы, устанавливающие свойства решений линейных систем.
Теорема:
Если X(t) является решением линейной однородной системы
то cX(t), где с — произвольная постоянная, является решением той же системы.
Теорема:
двух решений 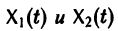
Следствие:
с произвольными постоянными коэффициентами сi решений 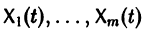
является решением той же системы.
Теорема:
Если 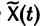
a Xo(t) — решение соответствующей однородной системы
будет решением неоднородной системы
Действительно, по условию,
Пользуясь свойством аддитивности оператора 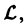
Это означает, что сумма 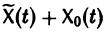
Определение:
называются линейно зависимыми на интервале a
при 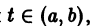

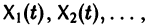
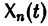
Заметим, что одно векторное тождество (5) эквивалентно n тождествам:
называется определителем Вронского системы векторов
Определение:
Пусть имеем линейную однородную систему
где 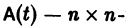
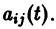
линейной однородной системы (6), линейно независимых на интервале а
с непрерывными на отрезке 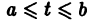
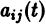
(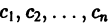
Пример:
имеет, как нетрудно проверить, решения
Эти решения линейно независимы, так как определитель Вронского отличен от нуля:
Общее решение системы имеет вид
(с1, с2 — произвольные постоянные).
Фундаментальная матрица
Квадратная матрица
столбцами которой являются линейно независимые решения 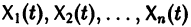
Если Х(t) — фундаментальная матрица системы (6), то общее решение системы можно представить в виде
— постоянная матрица-столбец с произвольными элементами. Полагая в (7) t = t0, имеем
Матрица 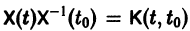
Теорема:
О структуре общего решения линейной неоднородной системы дифференциальных уравнений. Общее решение в области 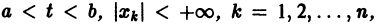
с непрерывными на отрезке 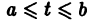
соответствующей однородной системы и какого-нибудь частного решения 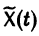
Метод вариации постоянных
Если известно общее решение линейной однородной системы (6), то частное решение неоднородной системы можно находить методом вариации постоянных (метод Лагранжа).
есть общее решение однородной системы (6), тогда
причем решения Xk(t) линейно независимы.
Будем искать частное решение неоднородной системы
где 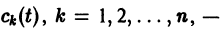
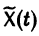
Подставляя 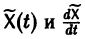
то для определения 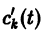
или, в развернутом виде,
Система (10) есть линейная алгебраическая система относительно 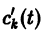
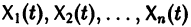
где 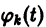
Подставляя эти значения 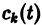
(здесь под символом 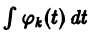
Системы линейных дифференциальных уравнений с постоянными коэффициентами
Рассмотрим линейную систему дифференциальных уравнений
в которой все коэффициенты 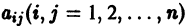
Мы рассмотрим еще метод Эйлера интегрирования линейных однородных систем дифференциальных уравнений с постоянными коэффициентами. Он состоит в следующем.
Метод Эйлера
Будем искать решение системы
где 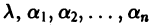
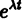
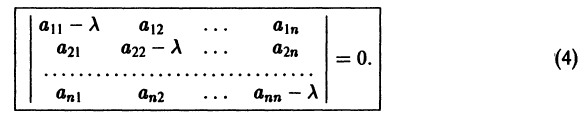
Для того, чтобы эта система (3) линейных однородных алгебраических уравнений с n неизвестными 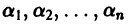
Уравнение (4) называется характеристическим. В его левой части стоит многочлен относительно 

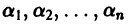
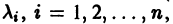
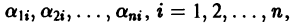
где второй индекс указывает номер решения, а первый — номер неизвестной функции. Построенные таким образом п частных решений линейной однородной системы (1)
образуют, как можно проверить, фундаментальную систему решений этой системы.
Следовательно, общее решение однородной системы дифференциальных уравнений (1) имеет вид
где 
Случай, когда характеристическое уравнение имеет кратные корни, мы рассматривать не будем.
Пример:
Ищем решение в виде
имеет корни
Система (3) для определения a1, а2 выглядит так:
Подставляя в (*) 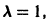
откуда а21 = а11. Следовательно,
Полагая в 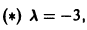
Общее решение данной системы:
Матричный метод
Изложим еще матричный метод интегрирования однородной системы (1). Запишем систему (1) в виде

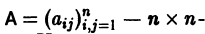
Напомним некоторые понятия из линейной алгебры. Вектор 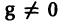
Число 
где I — единичная матрица.
Будем предполагать, что все собственные значения 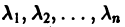
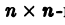
Столбцами матрицы Т являются координаты собственных векторов g1, g2 …, gn матрицы А.
Введем еще следующие понятия. Пусть В(t) — 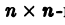
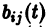
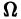
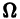
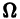
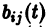
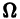
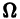
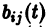
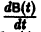
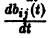
Пусть B(t) — n х n-матрица,
— вектор-столбец. Учитывая правила алгебры матриц, непосредственной проверкой убеждаемся в справедливости формулы
В частности, если В — постоянная матрица, то
так как 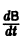
Теорема:
Если собственные значения 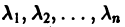
где g1, g2,…, gn — собственные векторы-столбцы матрицы А, 
Введем новый неизвестный вектор-столбец Y(t) по формуле
где Т — матрица, приводящая матрицу А к диагональному виду. Подставляя X(t) из (11) в (7), получим систему
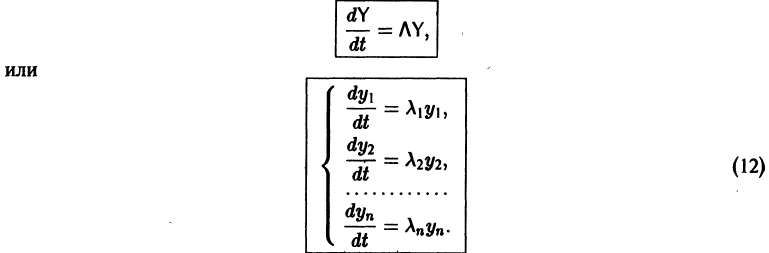
Умножая обе части последнего соотношения слева на 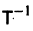
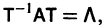
Мы получили систему из n независимых уравнений, которая без труда интегрируется:
Здесь 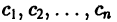
Вводя единичные n-мерные векторы-столбцы
решение Y(t) можно представить в виде
В силу (11) Х(t) = TY(t). Так как столбцы матрицы Т есть собственные векторы матрицы 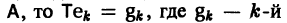
Таким образом, если матрица А системы дифференциальных уравнений (7) имеет различные собственные значения, для получения общего решения этой системы:
1) находим собственные значения 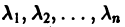
2) находим все собственные векторы g1, g2,…, gn;
3) выписываем общее решение системы дифференциальных уравнений (7) по формуле (10).
Пример:
Матрица А системы имеет вид
1) Составляем характеристическое уравнение
Корни характеристического уравнения
2) Находим собственные векторы
Для 
откуда g11 = g12, так что
Аналогично для 
3) Пользуясь формулой (10), получаем общее решение системы дифференциальных уравнений
Корни характеристического уравнения могут быть действительными и комплексными. Так как по предположению коэффициенты 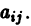
будет иметь действительные коэффициенты. Поэтому наряду с комплексным корнем 




При комплексном 
системы (7) также будет комплексным. Действительная часть
этого решения являются решениями системы (7). Собственному значению 



Пусть 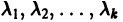
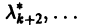
где сi — произвольные постоянные.
Пример:
1) Характеристическое уравнение системы
Его корни
2) Собственные векторы матриц
3) Решение системы
где а1, а2 — произвольные комплексные постоянные.
Найдем действительные решения системы. Пользуясь формулой Эйлера
Следовательно, всякое действительное решение системы имеет
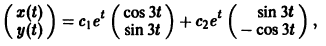
где с1, с2 — произвольные действительные числа.
Видео:Система неоднородных дифференциальных уравненийСкачать

Понятие о системах дифференциальных уравнений


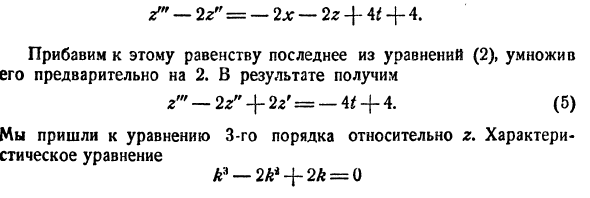

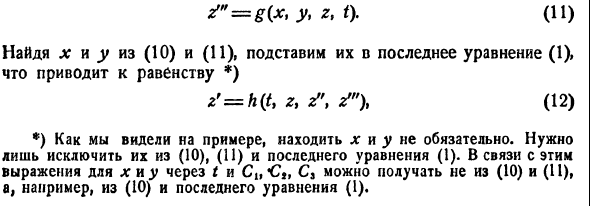

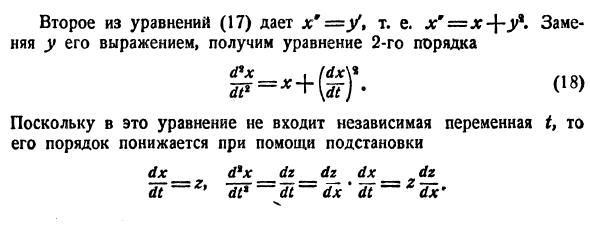

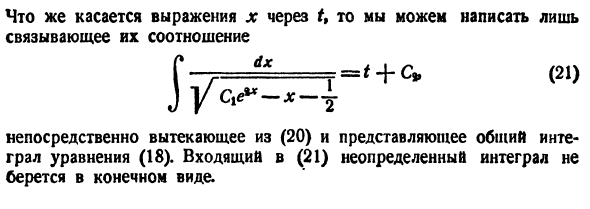

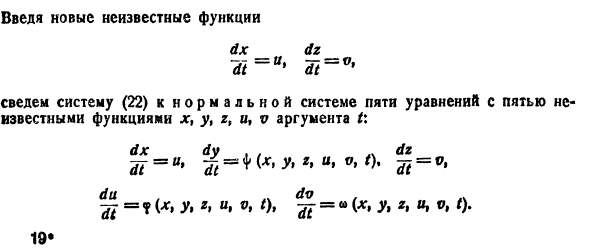
Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
📹 Видео
МЗЭ 2021 Лекция 11 Метод Ньютона для решения систем нелинейных уравненийСкачать

4.2 Решение систем нелинейных уравнений. МетодыСкачать

Нелинейная система дифференциальных уравненийСкачать

Видеоурок "Системы дифференциальных уравнений"Скачать

16. Линейные неоднородные дифференциальные уравнения 2-го порядка с постоянными коэффициентамиСкачать

Решение систем Д/У: 1. Знакомство с функциями odeXYСкачать

Системы дифференциальных уравнений. Метод исключенияСкачать

Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентамиСкачать

Системы дифференциальных уравнений. Часть 2Скачать

После этого видео, ТЫ РЕШИШЬ ЛЮБУЮ Систему Нелинейных УравненийСкачать

С.Г. Буланов. Компьютерная схема анализа устойчивости систем нелинейных дифференциальных уравненийСкачать

Линейное неоднородное дифференциальное уравнение с постоянными коэффициентами 4y''-y=x^3-24x #1Скачать

Системы дифференциальных уравнений. Метод исключения.Скачать

01.02. Модель SIR. Численное решение системы дифференциальных уравнений с помощью SciPyСкачать

Способы решения систем нелинейных уравнений. 9 класс.Скачать

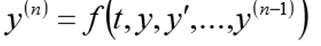
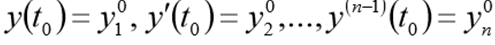


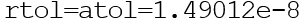
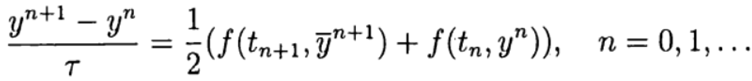
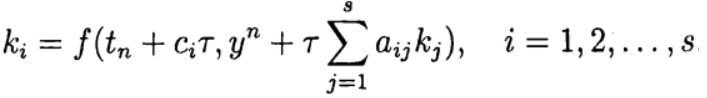
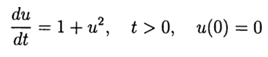 с использованием обеих функций def odein(),def oden() модуля scipy.integrate и адаптированного к Python методов Рунге—Кутта и Рунге—Кутта— Фельберга
с использованием обеих функций def odein(),def oden() модуля scipy.integrate и адаптированного к Python методов Рунге—Кутта и Рунге—Кутта— Фельберга