Содержание:
- Методы решения систем линейных алгебраических уравнений (СЛАУ)
- Метод Крамера
- Матричный способ решения СЛАУ
- Метод Гаусса
- Ранг матрицы. Теорема Кронекера-Капелли
- Следствия из теоремы Кронекера — Капелли
- Исследование СЛАУ. Общие сведения
- Общие сведения (определения, условия, методы, виды)
- Ранг матрицы и его свойства
- 20. Решение системы линейных уравнений с помощью ранга матрицы
- 📽️ Видео
Видео:11. Ранг матрицыСкачать

Методы решения систем линейных алгебраических уравнений (СЛАУ)
Метод Крамера
Определение: Системой линейных алгебраических уравнений (СЛАУ) называется выражение
Определение: Определитель, составленный из коэффициентов при неизвестных, называется главным определителем системы
Крамер предложил следующий метод решения СЛАУ: умножим главный определитель на 
Второй столбец умножим на 



Согласно записи СЛАУ первый столбец получившегося определителя представляет собой столбец свободных коэффициентов, т.е.
Определение: Определитель 
Поступая аналогично тому, как описано выше, найдем все вспомогательные определители СЛАУ:
31. Для того чтобы найти вспомогательный определитель i, надо в главном определителе СЛАУ заменить столбец i на столбец свободных коэффициентов.
Определение: Полученные выше соотношения называются формулами Крамера. Используя формулы Крамера, находят неизвестные величины 
- если главный определитель системы отличен от нуля (
), то система имеет единственное решение;
- если главный определитель системы равен нулю (
), а хотя бы один из вспомогательных определителей отличен от нуля (
или
, или, . или
), то система не имеет решений (деление на нуль запрещено);
- если все определители системы равны нулю (
), то система имеет бесчисленное множество решений.
Пример:
Решить СЛАУ методом Крамера
Решение:
Прежде всего, обращаем внимание на то, что в последнем уравнении переменные записаны в неправильном порядке, в этом случае говорят, что СЛАУ записана в ненормализованном виде. Нормализуем СЛАУ, для чего запишем неизвестные в последнем уравнении системы в правильном порядке, чтобы одноименные неизвестные были записаны друг под другом
Найдем главный определитель СЛАУ (раскрываем по первой строке)
Так как главный определитель системы отличен от нуля, то СЛАУ имеет единственное решение. Найдем три вспомогательных определителя
Воспользуемся формулами Крамера
Замечание: После нахождения решения СЛАУ надо обязательно провести проверку, для чего найденные числовые значения неизвестных подставляется в нормализованную систему линейных алгебраических уравнений.
Выполним проверку 
Матричный способ решения СЛАУ
Для решения СЛАУ матричным способом введем в рассмотрение матрицу, составленную из коэффициентов при неизвестных 

Тогда СЛАУ можно записать в матричном виде 





Пример:
Решить СЛАУ матричным способом
Решение:
Введем в рассмотрение следующие матрицы
Найдем матрицу 
Пример:
Решение:
Найдем алгебраические дополнения всех элементов 


Отсюда находим, что х = 1; y = l; z = l.
Метод Гаусса
Метод Гаусса или метод исключения неизвестных состоит в том, чтобы за счет элементарных преобразований привести СЛАУ к треугольному виду. Покажем использование расширенной матрицы, составленной из коэффициентов при неизвестных и расширенной за счет столбца свободных коэффициентов, для приведения СЛАУ к треугольному виду на примере системы, рассматриваемой в этой лекции. Расширенная матрица для СЛАУ имеет вид:
Замечание: В методе Гаусса желательно, чтобы первая строка расширенной матрицы начиналась с единицы.
Обменяем в расширенной матрице первую и вторую строки местами, получим 

Умножим элементы первой строки на (—1) и прибавим к соответствующим элементам третьей строки 

Из первого уравнения находим, что х = 1.
Вывод: Из вышеизложенного материала следует, что вне зависимости от
способа решения СЛАУ всегда должен получаться один и тот же ответ.
Замечание: После нахождения решения СЛАУ надо обязательно выполнить проверку, то есть подставить полученные значения неизвестных в заданную СЛАУ и убедиться в тождественности левой части всех равенств системы соответствующим правым частям. Отметим, что задание СЛАУ всегда верно, то есть, если проверка показывает нарушение оговоренной тождественности, то надо искать ошибку в проведенных вычислениях.
Ранг матрицы. Теорема Кронекера-Капелли
Определение: Рангом матрицы 
Если 
При вычислении ранга необходимо начинать вычислять миноры 2 порядка, затем миноры 3 порядка и так далее, пока не будут найдены миноры, обращающиеся в нуль. Если все миноры порядка p равны нулю, то и все миноры, порядок которых больше p, равны нулю.
Пример:
Найти ранг матрицы
Решение:
Очевидно, что среди миноров второго порядка есть миноры отличные от нуля, например, 


Теорема Кронекера-Капелли (критерий совместности СЛАУ). Для совместности системы линейных алгебраических уравнений (СЛАУ) необходимо и достаточно, чтобы ранг расширенной матрицы совпадал с рангом основной матрицы, составленной из коэффициентов при неизвестных величинах.
Видео:Ранг матрицыСкачать

Следствия из теоремы Кронекера — Капелли
Следствие: Если ранг матрицы совместной системы равен числу неизвестных, то система имеет единственное решение (то есть она определенная).
Следствие: Если ранг матрицы совместной системы меньше числа неизвестных, то система имеет бесчисленное множество решений (т.е. она неопределенная).
В случае неопределенной системы решения ищут следующим образом: выбираются главные неизвестные, число которых равно рангу, а остальные неизвестные считаются свободными; далее главные неизвестные выражаются через свободные и получают множество решений, зависящих от свободных неизвестных. Это множество решений называется общим решением системы. Придавая свободным неизвестным различные произвольные значения, получим бесчисленное множество решений, каждое из которых называется частным решением системы.
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Скалярное произведение и его свойства
- Векторное и смешанное произведения векторов
- Преобразования декартовой системы координат
- Бесконечно малые и бесконечно большие функции
- Критерий совместности Кронекера-Капелли
- Формулы Крамера
- Матричный метод
- Экстремум функции
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Видео:Математика без Ху!ни. Метод Гаусса. Совместность системы. Ранг матрицы.Скачать

Исследование СЛАУ. Общие сведения
В данной статье мы расскажем о методах, видах, условиях и определениях исследований решений систем линейных уравнений, что такое метод Кронекера-Капели, а также приведем примеры.
Видео:Решение системы уравнений методом Крамера.Скачать

Общие сведения (определения, условия, методы, виды)
Системы линейных алгебраических уравнений с n неизвестными могут иметь:
- единственное решение;
- бесконечное множество решение (неопределенные СЛАУ);
- ни одного решения (несовместные СЛАУ).
Пример 1
Система x + y + z = 1 2 x + 2 y + 2 z = 3 не имеет решений, поэтому она несовместна.
Система x + y = 1 2 x + 7 y = — 3 имеет единственное решение x = 2 ; y = 1 .
Система x + y = 1 2 x + 2 y = 2 3 x + 3 y = 3 имеет бесконечное множество решений x = t y = 1 — t при — ∞ t ∞ .
Перед решением системы уравнений необходимо исследовать систему, т.е. ответить на следующие вопросы:
- Совместна ли система?
- Если система совместна, то, какое количество решений она имеет — одно или несколько?
- Как найти все решения?
Если система малоразмерна при m = n , то ответить на поставленные вопросы можно при помощи метода Крамера:
- если основной определитель системы, то система совместна и имеет единственное решение, которое вычисляется методом Крамера;
- если, и один из вспомогательных определителей, то система не является совместной, т.е. не имеет решений;
- если и все, и один из коэффициентов СЛАУ, то система не является определенной и имеет бесконечное множество решений.
Видео:12. Метод Гаусса решения систем линейных уравнений. Часть 1.Скачать

Ранг матрицы и его свойства
Бывают случаи, которые выбиваются из представленных вариантов решения СЛАУ, например, линейные уравнения с большим количеством уравнений и неизвестных.
Для такого варианта решения существует ранг матрицы, который представляет собой алгоритм действий в случае решения системы матрицы, когда
В математике выделяют следующие подходы к определению ранга матрицы:
- при помощи понятия линейной зависимости/независимости строк/столбцов матрицы. Ранг равен максимальному количеству независимых строк (столбцов) матрицы
- при помощи понятия минора матрицы в качестве наивысшего порядка минора, который отличается от нуля. Минор матрицы порядка k — определитель k-го порядка, составленный из элементов, которые стоят на пересечении вычеркиваемых k-строк и k-столбцов матрицы;
- при помощи метода Гаусса. По завершении прямого хода ранг матрицы равняется количеству ненулевых строк.
Обозначение ранга матрицы: r ( A ) , r g ( A ) , r A .
Свойства ранга матрицы:
- квадратная невырожденная матрица обладает рангом, который отличается от нуля;
- если транспонировать матрицу, то ранг матрицы не изменяется;
- если поменять местами 2 параллельные строки или 2 параллельных столбца, ранг матрицы не изменяется;
- при удалении нулевого столбца или строки ранг матрицы не изменяется;
- ранг матрицы не изменяется, если удалить строку или столбец, которые являются линейной комбинацией других строк;
- при умножении все элементов строки/столбца на число k н е р а в н о н у л ю ранг матрицы не изменяется;
- ранг матрицы не больше меньшего из ее размеров: r ( А ) ≤ m i n ( m ; n ) ;
- когда все элементы матрицы равны нулю, то только тогда r ( A ) = 0 .
Пример 2
А 1 = 1 1 1 2 2 2 3 3 3 , B 1 = 1 0 0 0 0 0
r ( A 1 ) = 1 , r ( B 1 ) = 1
А 2 = 1 2 3 4 0 5 6 7 0 0 0 0 ; В 2 = 1 1 3 1 2 1 4 3 1 2 5 0 5 4 13 6
Видео:Матричный метод решения систем уравненийСкачать

20. Решение системы линейных уравнений с помощью ранга матрицы
Пусть дана система линейных уравнений 
Пусть А = 

Теорема 26 (теорема Кронекера – Капелли). Система линейных уравнений совместна тогда и только тогда, когда ранг её матрицы равен рангу расширенной матрицы.
Доказательство. Þ Пусть система (25) совместна. Следовательно, существуют такие элементы A1, A2, … , AN , что
Записав эти равенства в векторной форме, получим, что В = A1×А1 + A2×А2 + … + AN×АN , где А1, а2, … , АN –векторы-столбцы матрицы А, В – вектор-столбец свободных членов. Из последнего равенства следует, что системы векторов А1, а2, … , АN и А1, а2, … , АN , В эквивалентны, поэтому их ранги равны. Итак, rang A = rang A1.
Ü Пусть rang A = rang A1 = К. Не нарушая общности, можно считать, что отличный от нуля минор К-го порядка в матрице А Стоит в левом верхнем углу. Векторы-столбцы обозначим А1, а2, … , Ак, ак+1, … , АN, В (*). Система А1, а2, … , Ак Будет максимальной линейно независимой подсистемой в системе (*), следовательно, найдутся такие коэффициенты Х10, х20, … , хк0, Что В = Х10 А1 + Х20 А2 + … + Хк0 Ак. Это равенство равносильно равенству В = Х10 А1 + Х20 А2 + … + Хк0 Ак + … + 0×Ак+1 + … + 0×АN. Перейдя к координатам, получим:

Отсюда следует, что (Х10, х20, … , хк0, 0,… ,0) – решение системы (25), т. е. эта система совместна.
Из теоремы Кронекера – Капелли следуют правила решения системы линейных уравнений.
Для решения системы линейных уравнений достаточно
1. Найти ранги основной и расширенной матриц ( А и А1 ). Если rang A ¹ rang A1, То система не имеет решения.
2. Если rang A = rang A1 = К, то для решения достаточно оставить К Уравнений, коэффициенты которых стоят на тех строчках матрицы А, На которых стоит базисный минор, и в этих уравнениях оставить в их левых частях те неизвестные, коэффициенты которых входят в базисный минор. Остальные неизвестные нужно перенести в правые части уравнений. Они могут принимать все возможные значения из поля Р. Эти неизвестные называются Свободными. (Не нарушая общности, можно считать, что оставлены первые К уравнений и первые К неизвестных, система (29)).

Определитель левой части системы (29) отличен от нуля, число уравнений равно числу неизвестных, поэтому (по теореме Крамера) эта система при всевозможных Хк+1, … , хN имеет единственное решение.
📽️ Видео
Ранг матрицыСкачать

Урок 1. Матрицы, определитель матрицы и ранг матрицы | Высшая математика | TutorOnlineСкачать

15. Однородная система линейных уравнений / фундаментальная система решенийСкачать

Решение системы уравнений методом ГауссаСкачать

Как найти ранг матрицы (пример) - bezbotvyСкачать

Метод Крамера за 3 минуты. Решение системы линейных уравнений - bezbotvyСкачать

Теорема Кронекера-КапеллиСкачать

Математика без Ху!ни. Метод Гаусса.Скачать

Найти ранг матрицы при всех значениях параметраСкачать

Линейная алгебра, Матрицы: Метод Гаусса. Высшая математикаСкачать

ФСР. Система однородных уравнений. Общее решениеСкачать

Линейная алгебра, 6 урок, Ранг матрицыСкачать

Системы линейных уравнений: Теорема Кронекера-КапеллиСкачать







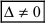 ), то система имеет единственное решение;
), то система имеет единственное решение;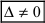 ), а хотя бы один из вспомогательных определителей отличен от нуля (
), а хотя бы один из вспомогательных определителей отличен от нуля ( 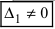 или
или 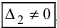 , или, . или
, или, . или 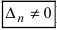 ), то система не имеет решений (деление на нуль запрещено);
), то система не имеет решений (деление на нуль запрещено);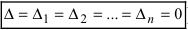 ), то система имеет бесчисленное множество решений.
), то система имеет бесчисленное множество решений.













