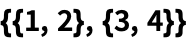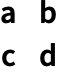Решение матричных уравнений вольфрам математика (3 видео)

Матрицы и линейная алгебра

В Языке Wolfram матрицы представляются как списки списков:

Их можно вводить в табличном виде, используя CTRL + ENTER для добавления строк и CTRL + , для добавления столбцов:

Out[2]=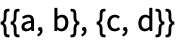

Решение матричных уравнений вольфрам математика

Функция MatrixForm позволяет отобразить матрицу в классическом виде:

Видео:Решение матричных уравненийСкачать

Решение матричных уравнений вольфрам математика

Операции линейной алгебры

Линейная алгебра — один из фундаментальных разделов математики. Он во многом способствовал развитию методов вычислений. Средства линейной алгебры (преобразование матриц, решение систем линейных уравнений и т. д.) широко используются при решении задач механики, электро- и радиотехники и других отраслей науки и техники. В этом разделе мы познакомимся с основным набором средств системы Mathematica, предназначенных для решения задач линейной алгебры.

Совокупность данных образует массив (Array). Массивы могут быть одномерными (один список), двумерными и многомерными (два и более списка). Одномерные массивы в математике называют векторами, двумерные — матрицами. В общем случае массив характеризуется размерностью (числом измерений) и размером — произведением числа элементов по всем размерностям. Mathematica позволяет создавать многомерные массивы — число элементов в них ограничено лишь объемом памяти компьютера.

Для задания массивов используются следующие функции:

Array [ f, n] — генерирует список длиной п с элементами f [ 1 ], f [ 2 ], . f[n];
Array [f, ] — генерирует массив размером n1x n2 x. в виде вложенных списков с элементами f [ i I, i2. ] (аргумент функции i k меняется от 1 до nk);
Array[f, dims, origin] — генерирует список с размерностью dims, используя спецификацию индекса origin;
Array [f, dims, origin, h] — использует заголовок h, а не List, для каждого уровня массива.

Далее приводятся примеры задания массивов и их вывода.

Y : =Array [Exp , 4 ]

Основные понятия линейной алгебры

Массивы, в основном в виде векторов и матриц, широко применяются при решении задач линейной алгебры. Прежде чем перейти к рассмотрению возможностей Mathematica в части решения таких задач, рассмотрим краткие определения, относящиеся к линейной алгебре.

Матрица — прямоугольная двумерная таблица, содержащая m строк и п столбцов элементов, каждый из которых может быть представлен числом, константой, переменной, символьным или математическим выражением (расширительная трактовка матрицы).

Квадратная матрица — матрица, у которой число строк m равно числу столбцов п. Пример квадратной матрицы размером 3×3:

Сингулярная (вырожденная) матрица — квадратная матрица, у которой детерминант (определитель) равен 0. Такая матрица обычно не упрощается при символьных вычислениях. Линейные уравнения с почти сингулярными матрицами могут давать большие погрешности при решении.

Единичная матрица — это квадратная матрица, у которой диагональные элементов равны 1, а остальные элементы равны 0. Ниже представлена единичная матрица размером 4×4:

1	0	0
0	1	0
E	=	0	1	0
0	0	1

Транспонированная матрица — квадратная матрица, у которой столбцы и строки меняются местами. Приведем простой пример.

a	b	c
A	=	d	e	f
i	k	l

a	d	i
А т	=	b	e	k
c	f	l

Обратная матрица — это матрица М -1 , которая, будучи умноженной на исходную квадратную матрицу М, дает единичную матрицу Е.

Ступенчатая форма матрицы соответствует условиям, когда первый ненулевой элемент в каждой строке есть 1 и первый ненулевой элемент каждой строки появляется справа от первого ненулевого элемента в предыдущей строке, то есть все элементы ниже первого ненулевого в строке — нули.

Диагональ матрицы — расположенные диагонально элементы А., матрицы А. В приведенной ниже матрице элементы диагонали представлены заглавными буквами:

A	b	c
А	=	d	E	f
i	k	L

Обычно указанную диагональ называют главной диагональю — для матрицы А, приведенной выше, это диагональ с элементами А, Е и L. Иногда вводят понятия поддиагоналей (элементы d и k) и наддиагоналей (элементы b к f).

Ранг матрицы — наибольший из порядков отличных от нуля миноров квадратной матрицы.

След матрицы — сумма диагональных элементов квадратной матрицы. Определитель матрицы — это многочлен от элементов квадратной матрицы, каждый член которого является произведением п элементов, взятых по одному из каждой строки и каждого столбца со знаком произведения, заданным четностью перестановок:

где M — определитель матрицы порядка n-1, полученной из матрицы А вычеркиванием первой строки и j-то столбца. В таком виде определитель (он же детерминант) легко получить в символьных вычислениях. В численных расчетах мы будем подразумевать под определителем численное значение этого многочлена.

Матрица в целой степени — квадратная матрица в степени п (п — целое неотрицательное число), определяемая следующим образом: М° = Е, М 1 = М, М 2 = = М*М. Мn = М n-1 -М.

Идемпотентная матрица — матрица, отвечающая условию Р 2 = Р.

Инволютивная матрица — матрица, отвечающая условию I 2 = Е.

Симметрическая матрица — матрица, отвечающая условию А т = А.

Кососимметрическая матрица — матрица, отвечающая условию А т = -А.

Ортогональная матрица — матрица, отвечающая условию А т = А- 1 .

Комплексно-сопряженная матрица — матрица А , полученная из исходной матрицы А заменой ее элементов на комплексно-сопряженные.

Эрмитова матрица — матрица А, удовлетворяющая условию А = А .

Собственный вектор квадратной матрицы А — любой вектор х е V n , х не равно 0, удовлетворяющий уравнению Ах = gx, где g — некоторое число, называемое собственным значением матрицы А.

Характеристический многочлен матрицы — определитель разности этой матрицы и единичной матрицы, умноженный на переменную многочлена — |А — g Е|.

Собственные значения матрицы — корни ее характеристического многочлена.

Норма — обобщенное понятие абсолютной величины числа. Норма трехмерного вектора ||х|| — его длина. Норма матрицы — значение sup(||Ax||/||x||). I-норма матрицы А — число

Матричная форма записи системы линейных уравнений — выражение А-Х = В, где А — матрица коэффициентов системы, X — вектор неизвестных, и В — вектор свободных членов. Один из способов решения такой системы очевиден — X = А -1 В, где А- 1 — обратная матрица.

Функции линейной алгебры

Следующая группа функций системы Mathematica позволяет осуществлять над векторами и матрицами основные операции, используемые в линейной алгебре:

Cross [vl,v2, v3. ] — векторное произведение (может задаваться в виде v1*v2*v3*. );
Det [m] — возвращает детерминант (определитель) квадратной матрицы m;
DiagonalMatrix [list] — возвращает диагональную матрицу с главной диагональю, сформированной из элементов списка list, и нулевыми остальными элементами матрицы;
Dot [a, b, с] — возвращает произведения векторов, матриц и тензоров. Операцию произведения можно задавать также в виде а. b. с;
Eigensystem[m] — возвращает список собственных значений и собственных векторов квадратной матрицы т;
Eigenvalues [m] — возвращает список собственных значений квадратной матрицы m;
Eigenvectors [m] — возвращает список собственных векторов квадратной матрицы m;
IdentityMatrix [n] — возвращает единичную матрицу размером пхп (у нее диагональные элементы имеют значения 1, остальные 0);
Inverse [m] — возвращает обратную матрицу для квадратной матрицы т, то есть матрицу m- 1 , которая, будучи умноженной на исходную матрицу, дает единичную матрицу;
LinearSolve [m, b] — возвращает вектор х, представляющий собой решение матричного уравнения m. x==b, где m — матрица коэффициентов левой части системы линейных уравнений, х — вектор неизвестных и b — вектор свободных членов в правой части системы;
Tr [list] — возвращает след матрицы или тензора (эта функция есть только у Mathematica 4);
Transpose [m] — возвращает транспонированную матрицу, у которой столбцы и строки меняются местами в сравнении -с исходной матрицей m;
RowReduce [m] — производит гауссовское исключение переменных, возвращая упрощенную форму матрицы m, полученную путем линейного комбинирования строк.

Следующие примеры иллюстрируют применение основных из этих функций.

Видео:Лекция 8. Решение матричных уравненийСкачать

7. Уравнения и системы уравнений

Уравнения и системы уравнений

Многие математические задачи сводятся к решению в общем случае нелинейных уравнений вида f(x) = 0 или f(x) = expr.

В системе Mathematica они обозначаются как eqns (от слова equations — уравнения). Разумеется, могут решаться и системы, состоящие из ряда таких уравнений.

Для решения уравнений (как одиночных, так и систем) в численном и символьном виде Mathematica имеет функцию Solve:

Solve [eqns, vars] — предпринимает попытку решить уравнение или систему уравнений eqns относительно переменных vars;
Solve [eqns, vars, elims] — пытается решать уравнения eqns по переменным vars, исключая переменные elims.

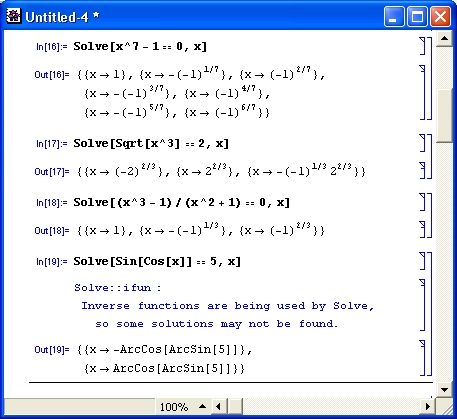
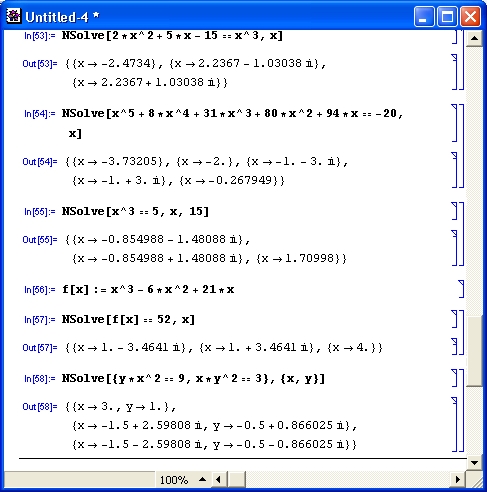
Входные параметры этой функции могут быть представлены списками или записаны выражениями через объединительный знак«&&». В eqns в качестве знака равенства используется знак «= =». Примеры применения функции Solve представлены на рис. 4.12.

Рис. 4.12. Примеры решения уравнений

Обратите внимание на то, что в определенных ситуациях система подсказывает тонкости решения, выдавая предупреждающие сообщения. Если такие ситуации не являются ошибками, препятствующими решению, то полученное решение выводится в ячейку вывода.

Решение систем нелинейных уравнений в символьном виде

Приведенные на рис. 4.13 примеры показывают решение систем нелинейных уравнений с помощью функции Solve.

Достаточно характерен пример с применением функции N. Если убрать в нем функцию N, то будет получен чрезвычайно громоздкий, хотя и точный результат (проверьте это сами, поскольку размеры результата делают нецелесообразным его приведение в книге). Функция N осуществляет выполнение всех промежуточных вычислений, благодаря чему результат получается вполне обозримым и представленным в комплексных числах.

В последнем примере рис. 4.13 получен набор из пяти пар корней, определенных через функцию Root. Эта функция, в свою очередь, означает вычисление корней полиномиального уравнения пятой степени. Данный пример, как и ранее приводимые решения кубического уравнения, является наглядной иллюстрацией того, что простота нелинейных уравнений порой оказывается весьма обманчивой, а их решение порой приводит к весьма громоздким и сложным результатам. Тем не менее, возможность решения отдельных нелинейных уравнений и их систем в символьном виде трудно переоценить. К сожалению, далеко не все уравнения имеют такие решения — многие можно решать только в численном виде.

Рис. 4.13. Примеры решения систем нелинейных уравнений

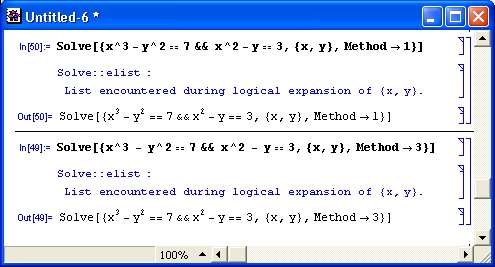
Не следует полагать, что Mathematica всегда выдает верное решение систем нелинейных уравнений. На самом деле решение иногда бывает ошибочным. Поэтому в большинстве случаев стоит оформлять решение таким образом, чтобы обеспечить его проверку. Для этого рекомендуется отдельно задать систему уравнений и результат решения. Тогда проверка легко осуществляется с помощью подстановки. Два примера решения систем уравнений с проверкой решений показаны на рис. 4.14.

В первом примере решение кажется очевидным (равенства выполняются, например, при х=2 и у=3). Однако здесь Mathematica дает сразу три пары решений, и все они оказываются верны, поскольку после подстановки проверка всех равенств возвращает True.

А вот во втором примере проверка дала не совсем обычный результат, что связано с наличием в решении неопределенной переменной а. В таких случаях стоит попробовать упростить решение с помощью функции Simplify, что и показано на рис. 4.14.

Рис. 4.14. Примеры решения уравнений с проверкой

Опции функции Solve

С функцией Solve можно использовать ряд опций. Их можно вывести командой Options [Solve]. Ниже описано их назначение:

InverseFunctions — указывает, следует ли использовать обратные функции;
MakeRules — указывает, должен ли результат быть представлен как объект AlgebraicRulesData;
Method — устанавливает алгоритм, используемый для вычисления результата (возможны методы 1, 2 и 3);
Mode — задает характер решения уравнения (возможны Generic, Modular и Rational);
Sort — устанавливает, нужна ли сортировка результатов;
Verif ySolutions — устанавливает, следует ли проводить проверку полученных решений и удаление посторонних решений;
WorkingPrecision — устанавливает число цифр промежуточных вычислений (по умолчанию Infinity).

На рис. 4.15 приведены примеры применения функции Solve с опцией Inverse-Functions.

Обратите внимание на то, что последняя система уравнений при отсутствии опции InverseFunctions решается с предупреждением. Она вообще не решается, если эта опция задана как False, и гладко решается при InverseFunctions -> True.

Рис. 4.15. Примеры решения уравнений с опцией InverseFunction

То, насколько может влиять на решение опция Method, наглядно показывают примеры, представленные на рис. 4.16.

Рис. 4.16. Примеры решения уравнений разными методами

Множество примеров решения систем нелинейных уравнений в символьном виде можно найти в справочной системе Mathematica.

Численное решение уравнений

Многие нелинейные уравнения и системы нелинейных уравнений в принципе не имеют аналитических решений. Однако их решение вполне возможно численными методами. Для численного решения систем нелинейных уравнений используется функция NSolve:

NSolve [eqns, vars] — пытается численно решить одно уравнение или систему уравнений eqns относительно переменных vars;
NSolve [eqns, vars, elims] — пытается численно решить уравнения eqns относительно vars, исключая переменные elims.

С этой функцией используется единственная опция WorkingPrecision, задающая число верных цифр результата — по умолчанию 16. На рис. 4.17 представлены примеры использования функции NSolve для численного решения уравнений.

Риc. 4.17. Примеры численного решения уравнений

Результаты решения с помощью функции NSolve также рекомендуется проверять с помощью подстановки, например, так:

Нетрудно заметить, что в данном случае решение верно.

Поиск корней уравнений

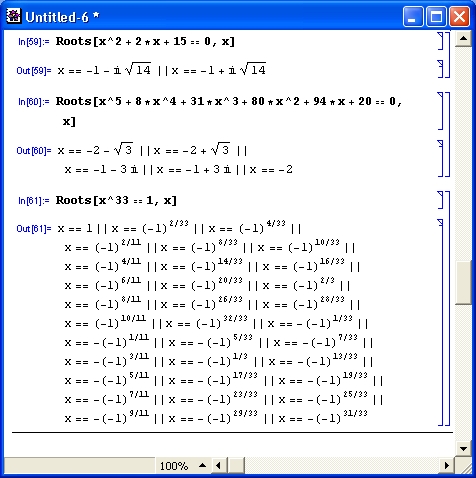
Для вычисления корней полиномиальных уравнений используется функция Roots:

На рис. 4.18 представлены примеры применения функции Roots.

Рис. 4.18. Примеры использования функции Roots

Формат выдачи результатов для функции Roots отличается от такового для функции Solve. Поэтому проверку решения подстановкой надо выполнять как в следующем примере:

х == -3.56155 | | х == 0.561553

Для преобразования результата вычислений в список решений (подобный решениям, получаемым с помощью функции Solve) здесь использована функция ToRules.

При затруднениях в решении уравнений с помощью функции Roots можно использовать следующие опции:

True, Eliminate -> False, EquatedTo-> Null,

Modulus -> 0, Multiplicity->1, Quar tics -> True, Using -> True>

Ниже они описаны подробно:

Cubics — указывает, следует ли искать явные решения для неприводимых кубических уравнений;
EquatedTo — задает выражение для замещения переменной в решении;
Modulus — задает промежуточную факторизацию полинома;
Multiplicity— устанавливает кратность каждого из корней в конечном результате;
Quartics — задает точное решение квадратного уравнения и полинома четвертой степени;
Using — указывает какие-либо дополнительные уравнения, которые следует использовать для решения уравнений.

Применение опций нередко позволяет получать решения, которые не удаются с первого раза. Однако это требует определенного опыта и понимания сути решаемой задачи.

Дополнительные функции для решения уравнений

Имеется также ряд дополнительных функций, которые используются описанными ранее функциями и также могут применяться при решении нелинейных уравнений:

Auxiliary [v] — применяется модулем Solve для указания того, что переменная v должна использоваться функцией Roots для результирующих решений, но соответствующие значения v не должны быть включены в окончательный ответ;
Eliminate [eqns, vars] — исключает переменные vars из системы уравнений eqns;
FindRoot [Ihs == rhs, ] — ищет численное решение уравнения Ihs == rhs, начиная с х = x0;
MainSolve [eqns] — основная функция для преобразования системы уравнений. Ее вызывают Solve и Eliminate. Уравнения должны быть представлены в форме Ihs == rhs. Они могут объединяться с помощью && и | |. MainSolve возвращает False, если не существует решения уравнений, и возвращает True, если все значения переменных являются решениями. MainSolve перестраивает уравнения, применяя определенные директивы;
MainSolve [eqns, vars, elim, rest] — пытается перестраивать уравнения eqns так, чтобы найти решения для переменных vars и исключить переменные elim. Список rest может включаться для указания порядка исключения любых остальных переменных;
NRoots [lhs==rhs, var] — возвращает список численных приближений корней полиномиального уравнения;
Residue [ехрr, ] — ищет вычет ехрг в точке х = х0;
SolveAlways [eqns, vars] — возвращает значения параметров, которые превращают уравнения eqns в тождества для всех значений переменных vars.

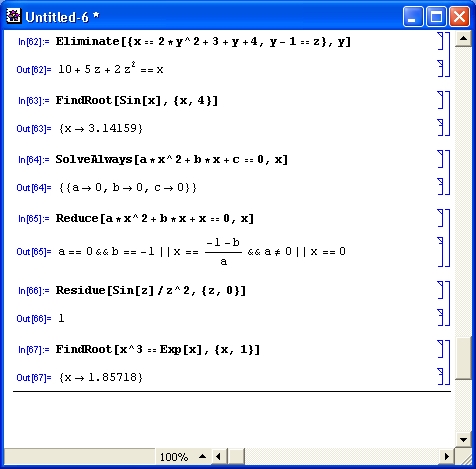
Примеры использования некоторых из этих функций показаны на рис. 4.19.

Рис. 4.19. Примеры применения дополнительных функций для решения уравнений

В целом надо отметить, что система Mathematica обладает обширными средствами для решения уравнений и их систем. Умение их применять — залог правильного и эффективного решения сложных математических задач, относящихся к классу решения уравнений.

Графическая иллюстрация и выбор метода решения уравнений

При рассмотрении приведенных выше примеров может сложиться благодушное впечатление о том, что решение нелинейных уравнений может производиться автоматически и без размышлений. Но это далеко не так — представленные выше примеры просто подобраны так, что они имеют решение с помощью соответствующих функций.

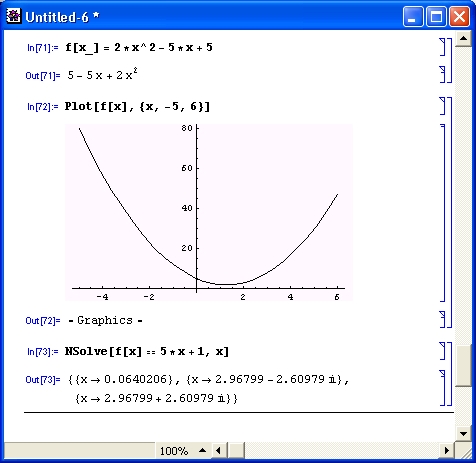
На самом деле порой даже простые уравнения могут не иметь решения. В сложных случаях очень полезна графическая визуализация решения. В качестве примера на рис. 4.20 показана визуализация вычисления корней квадратного уравнения. В данном случае график функции явно указывает на существование двух действительных корней при х, близких к 0.2 и 2.3. Функция Nsolve без труда находит оба корня.

Рис. 4.20. Визуализация решения квадратного уравнения для случая двух действительных корней

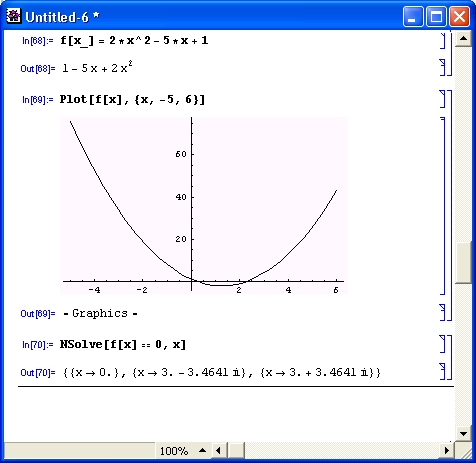
А вот на рис. 4.21 показан случай, когда из-за изменения последнего члена квадратичной функции ее график уже не пересекает ось х вообще. Это говорит о том, что решения в виде действительных корней нет. И в самом деле, NSolve находит корни как комплексно-сопряженные числа. Действительная часть найденных корней дает координату х для впадины кривой — параболы.

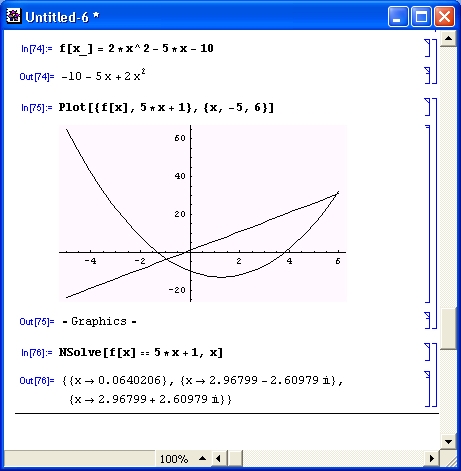
Если требуется решение равенства f1(х) = f ₂ (x), то для графической визуализации решения можно построить графики функций f1(х) и f ₂ (лг) — наличие точек их пересечения будет означать существование действительных корней. Этот случай иллюстрирует рис. 4.22. В данном случае проблем с решением нет, поскольку, по существу, решается квадратное уравнение.

Рис. 4.21. Визуализация решения квадратного уравнения для случая двух комплексных корней

Рис. 4.22. Пример визуализации решения уравнения вида f(x) = 5х + 1

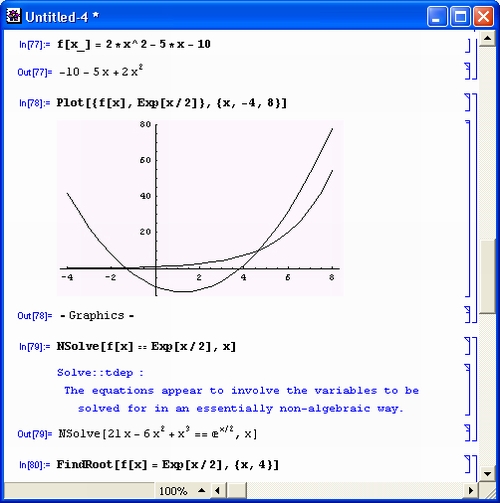
Но вот на рис. 4.23 показан случай решения уравнения f(x) = ехр(х/2). Графики функций ясно показывают, что парабола пересекается экспонентой в двух точках. Однако функция NSolve отказывается решать такое уравнение и выдает сообщение о том, что оно является трансцендентным.

Таким образом, в данном случае наличие графического решения говорит о необходимости смены функции, с помощью которой до сих пор решались уравнения. Подходящей в данном случае является функция FindRoot, которая отыскивает одно решение вблизи заданной начальной точки. Применив ее дважды, нетрудно получить оба корня данного уравнения.

Рис. 4.23. Пример решения уравнения вида f(x) = ехр(х/2)

Приведенные примеры далеко не исчерпывают проблему графической визуализации решения и выбора методов решения. Однако они иллюстрируют возможности системы Mathematica в этой области и заостряют внимание на потенциальных проблемах. Для реализации численных расчетов в системе Mathematica отобраны наилучшие и наиболее эффективные численные методы из описанных в литературе, в том числе в отечественной.

Получение сразу нескольких корней

Многие уравнения с тригонометрическими функциями могут иметь периодические или близкие к ним решения. К сожалению, функции Mathematica, вычисляющие корни уравнений, не способны в этом случае дать сразу несколько корней. Однако ситуация тут далеко не безнадежна — приведенный ниже пример наглядно показывает это.

Пусть требуется в интервале изменения х от 0 до 20 найти все решения уравнения

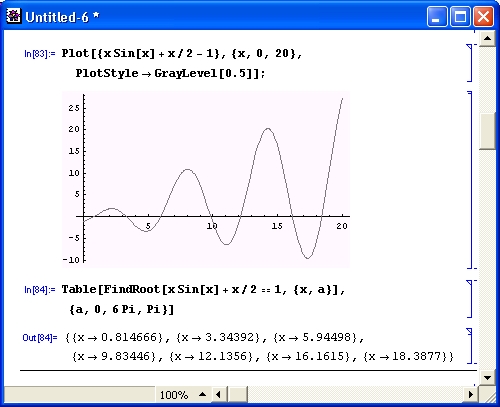
График функции, представляющей левую часть уравнения, показан на рис. 4.24. Хорошо видно, что он пересекает ось х семь раз, то есть имеет в интересующем нас диапазоне семь корней.

Рис. 4.24. График функции х sin(x) + х/2 — 1 и пример вычисления всех ее корней в интервале изменения х от 0 до 20

Колебательная составляющая функции обусловлена входящей в нее функцией sin(x), которая имеет нули в точках 0, n, 2n, Зn. Однако, как видно из рис. 4.24, эти значения лишь приближенные, ввиду влияния других членов уравнения.

Ключевая идея получения всех корней уравнения заключается в поиске нужных решений с помощью функции FindRoot, которой последовательно подставляются различные начальные приближения. Однако вместо уже испытанного приема — поиска корней поодиночке — можно воспользоваться «таблицей» решений, используя функцию Table. Решение, приведенное под графиком функции на рис. 4.24, наглядно иллюстрирует возможности этого приема — найдены (или, вернее, уточнены) все семь корней исходного уравнения.

Получение неизвестных в явном виде

Читатель, возможно, обратил внимание на то, что решения всех представленных выше примеров выглядят не совсем обычно — в виде списка подстановок. Это не позволяет использовать неизвестные в явном виде, например, для проверки решений или передачи найденных неизвестных в последующие вычислительные блоки. Однако от этого затруднения легко избавиться, если перед конструкций блока решения использовать выражение следующего вида:

Список переменных в этом выражении должен однозначно соответствовать списку неизвестных системы уравнений. Покажем этот прием в действии. Ниже приведено решение системы из трех нелинейных уравнений:

Обратите внимание на то, что вывод списка не дает полученных значений неизвестных. Это связано с тем, что переменные в блоке решения имеют ло-к(1лъный характер и за пределами блока их значения (в том числе неопределенные) сохранятся такими, какими они были до применения в блоке решения.

Теперь зададим решение в ином виде:

Как видите, на сей раз решение получено в виде списка с числами — явными значениями неизвестных. Можно обозначить их как а, Ь и с, получить список и даже использовать их отдельно:

Теперь можно проверить решение данной системы:

Полученный вектор правых частей системы совпадает с заданным, что свидетельствует о правильности решения. Разумеется, вместо нового списка для вектора решения можно было использовать и вектор .