Решение матричных уравнений в матлабе

Доброго времени суток, читатели! Сегодня мы поговорим о матрицах в Matlab, об их применении в решении систем линейных алгебраических уравнений. Подробно разберем методы решения, и для этого необходимо знание нескольких базовых алгоритмов.

Также стоит отметить, что у каждого алгоритма, которым мы будем искать решение СЛАУ в Matlab, своя скорость нахождения этого решения, наличие или отсутствие условия выполнения алгоритма и т.д.

В традициях нашего сайта разберём на примере:

Решить систему линейных уравнений:

4*a + b — c = 6
a — b + c = 4
2*a — 3*b — 3*c = 4

Видео:MATLAB 04 Массивы и матрицыСкачать

Метод обратной матрицы в Matlab

Начнем с достаточно распространенного метода. Его суть состоит в том, что сначала необходимо выписать коэффициенты при a, b и c (то есть те коэффициенты, которые находятся слева) в одну матрицу, а свободный член (то есть то, что справа) в другую.

В итоге у нас получится 2 матрицы:

Для реализации этого метода (и следующих методов тоже) требуется одно условие: чтобы определитель матрицы, составленной из коэффициентов левой части не был равен нулю. Проверка на определитель:

После проверки условия можем перейти к следующему шагу: нахождение обратной матрицы. В Matlab для этого используется оператор inv .
А само решение СЛАУ в Matlab находится как перемножение найденной обратной матрицы на матрицу свободных членов:

Мы получили 3 значения, которые и соответствуют нашим коэффициентам: то есть a = 2, b = -1, c = 1 . Можете проверить, подставив полученные ответы в исходную систему, и убедиться, что мы решили СЛАУ правильно.

Также следует отметить, что матрицы нужно перемножать именно, как сделали мы, то есть слева обратная матрица, справа матрица свободных членов.

Если вы не все поняли, то советую вам почитать нашу статью по основам Matlab.

Видео:2 - Решениt систем линейных алгебраических уравнений (СЛАУ) с помощью Matlab.Скачать

Метод Гаусса

Метод Гаусса в Matlab реализуется достаточно просто: для этого нам нужно всего лишь изучить один новый оператор.
() — левое деление.
При следующей записи:

Мы получим ответы на нашу исходную систему. Только заметьте, мы решили СЛАУ стандартным набором функций в Matlab, и желательно этот оператор использовать когда матрица коэффициентов квадратная, так как оператор приводит эту матрицу к треугольному виду. В других случаях могут возникнуть ошибки.

Видео:Решение матричных уравненийСкачать

Метод разложения матрицы

Теперь поговорим о разложении матрицы. Нахождение решения через разложение матрицы очень эффективно. Эффективность обусловлена скоростью нахождения решения для данного вида систем и точностью полученных результатов.

Возможны следующие разложения:

• разложение Холецкого
• LU разложение
• QR разложение

Разберём решение через LU и QR разложение, так как в задачах чаще всего встречается задание на решение именно через такие разложения.

Основное отличие этих двух разложений: LU разложение применимо только для квадратных матриц, QR — возможно и для прямоугольных.

LU разложение

Решим выше предложенную задачу через LU разложение:

QR разложение

И через QR разложение соответственно:

Отметим, что апостроф ( ‘ ) после Q означает транспонирование.

Видео:Математика это не ИсламСкачать

Стандартные функции Matlab

Так же Matlab предлагает функцию linsolve , с помощью которой возможно решить систему линейных алгебраических уравнений. Выглядит это так:

Как видите, ничего сложного тут нет, на то они и стандартные функции Matlab.

Видео:Решение трёх систем линейных уравнений в MatLabСкачать

Повторение

Итак, сегодня мы с вами изучили несколько методов для решения СЛАУ в Matlab, как с помощью матриц, так и с помощью стандартных функций. Давайте их повторим на другом примере:

Решить систему линейных уравнений:
6*a — b — c = 0
a — 2*b + 3*d = 0
3*a — 4*b — 4*c = -1

• Методом обратной матрицы:
• Методом Гаусса:
• LU разложение:
• QR разложение:

На этом я с вами попрощаюсь, надеюсь, вы научились применять матрицы в Matlab для решения СЛАУ.

Видео:Системы уравнений, определители, обращение матриц. Методы вычислений в MATLAB. Урок 73Скачать

mldivide ,

Solve systems of linear equations Ax = B for x

Видео:Лекция 8. Решение матричных уравненийСкачать

Syntax

Видео:Решение произвольных уравнений. Методы вычислений в MATLAB. Часть 1. Урок 61Скачать

Description

x = A B solves the system of linear equations A*x = B . The matrices A and B must have the same number of rows. MATLAB ® displays a warning message if A is badly scaled or nearly singular, but performs the calculation regardless.

If A is a scalar, then AB is equivalent to A.B .

If A is a square n -by- n matrix and B is a matrix with n rows, then x = AB is a solution to the equation A*x = B , if it exists.

If A is a rectangular m -by- n matrix with m

= n , and B is a matrix with m rows, then A B returns a least-squares solution to the system of equations A*x= B .

x = mldivide( A , B ) is an alternative way to execute x = A B , but is rarely used. It enables operator overloading for classes.

Видео:§29 Решение матричного уравненияСкачать

Examples

System of Equations

Solve a simple system of linear equations, A*x = B .

Linear System with Singular Matrix

Solve a linear system of equations A*x = b involving a singular matrix, A .

When rcond is between 0 and eps , MATLAB® issues a nearly singular warning, but proceeds with the calculation. When working with ill-conditioned matrices, an unreliable solution can result even though the residual (b-A*x) is relatively small. In this particular example, the norm of the residual is zero, and an exact solution is obtained, although rcond is small.

When rcond is equal to 0 , the singular warning appears.

In this case, division by zero leads to computations with Inf and/or NaN , making the computed result unreliable.

Least-Squares Solution of Underdetermined System

Solve a system of linear equations, A*x = b .

Linear System with Sparse Matrix

Solve a simple system of linear equations using sparse matrices.

Consider the matrix equation A*x = B .

Видео:1 - Решение систем нелинейных уравнений в MatlabСкачать

Input Arguments

A , B — Operands
vectors | full matrices | sparse matrices

Operands, specified as vectors, full matrices, or sparse matrices. A and B must have the same number of rows.

If A or B has an integer data type, the other input must be scalar. Operands with an integer data type cannot be complex.

Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64 | logical | char
Complex Number Support: Yes

Видео:Решение произвольных уравнений. Методы вычислений в MATLAB. Часть 2. Урок 62Скачать

Output Arguments

x — Solution
vector | full matrix | sparse matrix

Solution, returned as a vector, full matrix, or sparse matrix. If A is an m -by- n matrix and B is an m -by- p matrix, then x is an n -by- p matrix, including the case when p==1 .

If A has full storage, x is also full. If A is sparse, then x has the same storage as B .

The operators / and are related to each other by the equation B/A = (A’B’)’ .

If A is a square matrix, then AB is roughly equal to inv(A)*B , but MATLAB processes AB differently and more robustly.

If the rank of A is less than the number of columns in A , then x = AB is not necessarily the minimum norm solution. You can compute the minimum norm least-squares solution using x = lsqminnorm (A,B) or x = pinv (A)*B .

Use decomposition objects to efficiently solve a linear system multiple times with different right-hand sides. decomposition objects are well-suited to solving problems that require repeated solutions, since the decomposition of the coefficient matrix does not need to be performed multiple times.

Видео:Обращение матриц. Решение задачи Коши. Методы вычислений в MATLAB. Часть 1. Урок 75Скачать

Algorithms

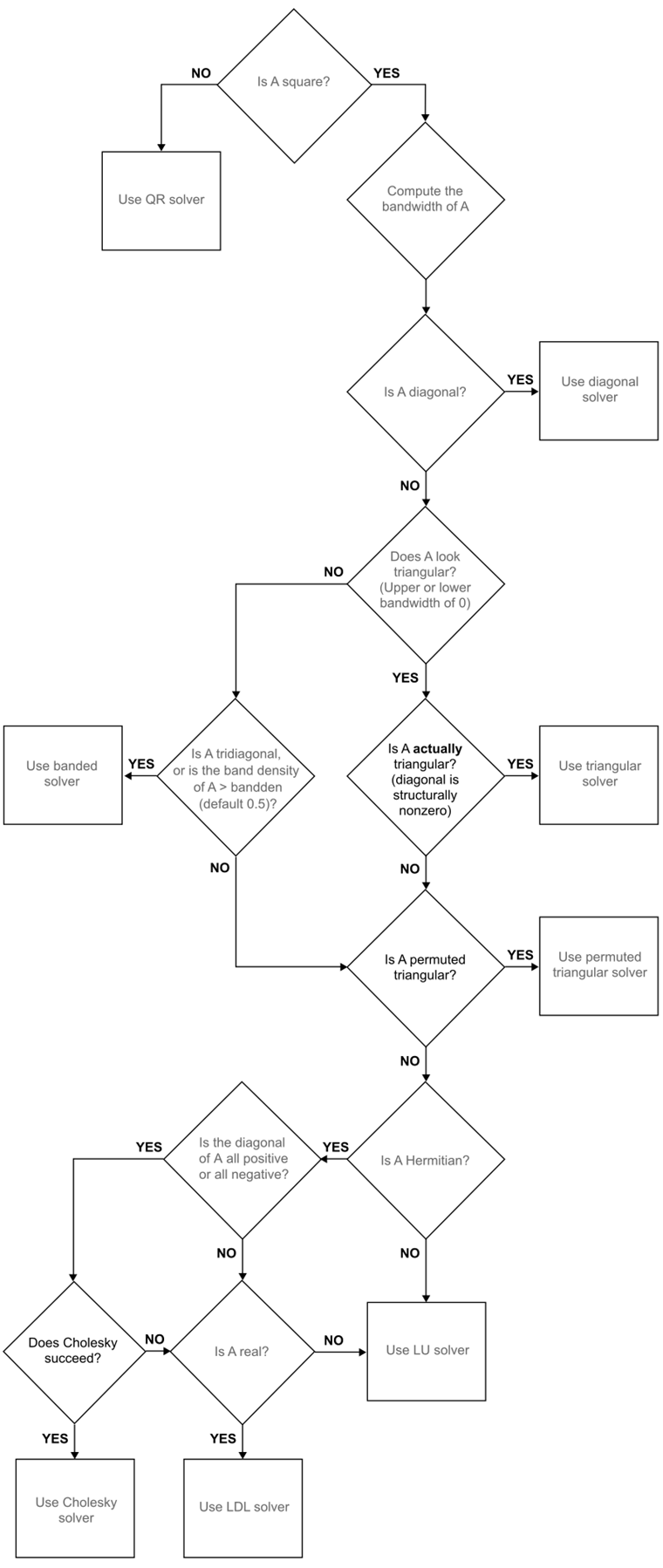
The versatility of mldivide in solving linear systems stems from its ability to take advantage of symmetries in the problem by dispatching to an appropriate solver. This approach aims to minimize computation time. The first distinction the function makes is between full (also called “ dense ”) and sparse input arrays.

Algorithm for Full Inputs

The flow chart below shows the algorithm path when inputs A and B are full.

Algorithm for Sparse Inputs

If A is full and B is sparse then mldivide converts B to a full matrix and uses the full algorithm path (above) to compute a solution with full storage. If A is sparse, the storage of the solution x is the same as that of B and mldivide follows the algorithm path for sparse inputs, shown below.

Видео:Как в MATLAB Simulink моделировать уравнения (Структурная схема САУ)Скачать

Extended Capabilities

Tall Arrays
Calculate with arrays that have more rows than fit in memory.

This function supports tall arrays with the limitation:

For the syntax Z = XY , the array X must be a scalar or a tall matrix with the same number of rows as Y .

C/C++ Code Generation
Generate C and C++ code using MATLAB® Coder™.

Usage notes and limitations:

For sparse matrix inputs, the language standard must be C99 or later.

GPU Code Generation
Generate CUDA® code for NVIDIA® GPUs using GPU Coder™.

Usage notes and limitations:

For sparse matrix inputs, the language standard must be C99 or later.

Thread-Based Environment
Run code in the background using MATLAB® backgroundPool or accelerate code with Parallel Computing Toolbox™ ThreadPool .

This function fully supports thread-based environments. For more information, see Run MATLAB Functions in Thread-Based Environment.

GPU Arrays
Accelerate code by running on a graphics processing unit (GPU) using Parallel Computing Toolbox™.

Usage notes and limitations:

If A is rectangular, then it must also be nonsparse.

The MATLAB mldivide function prints a warning if A is badly scaled, nearly singular, or rank deficient. The gpuArray mldivide is unable to check for this condition. Take action to avoid this condition.

64-bit integers are not supported.

For more information, see Run MATLAB Functions on a GPU (Parallel Computing Toolbox) .

Distributed Arrays
Partition large arrays across the combined memory of your cluster using Parallel Computing Toolbox™.

Usage notes and limitations:

The MATLAB mldivide function prints a warning if A is badly scaled, nearly singular, or rank deficient. The distributed array mldivide is unable to check for this condition. Take action to avoid this condition.

If A is an M-by-N complex matrix with N > M, for distributed arrays, mldivide computes a solution that minimizes norm(X) . The result is the same as the result of PINV(A)*B .

For more information, see Run MATLAB Functions with Distributed Arrays (Parallel Computing Toolbox) .

Видео:MatLab. Решение дифференциального уравнения.Скачать

MATLAB — алгебра

До сих пор мы видели, что все примеры работают как в MATLAB, так и в его GNU, альтернативно называемом Octave. Но для решения основных алгебраических уравнений и MATLAB, и Octave немного отличаются, поэтому мы постараемся охватить MATLAB и Octave в отдельных разделах.

Мы также обсудим факторизацию и упрощение алгебраических выражений.

Видео:Матричные уравнения Полный разбор трех типов матричных уравненийСкачать

Решение основных алгебраических уравнений в MATLAB

Функция решения используется для решения алгебраических уравнений. В простейшем виде функция решения принимает в качестве аргумента уравнение, заключенное в кавычки.

Например, давайте решим для х в уравнении х-5 = 0

MATLAB выполнит приведенный выше оператор и вернет следующий результат —

Вы также можете вызвать функцию решения как —

MATLAB выполнит приведенный выше оператор и вернет следующий результат —

Вы можете даже не включать правую часть уравнения —

MATLAB выполнит приведенный выше оператор и вернет следующий результат —

Если в уравнение входит несколько символов, то по умолчанию MATLAB предполагает, что вы решаете для x, однако функция решения имеет другую форму —

где вы также можете упомянуть переменную.

Например, давайте решим уравнение v — u — 3t 2 = 0, для v. В этом случае мы должны написать —

MATLAB выполнит приведенный выше оператор и вернет следующий результат —

Видео:MatLab. 6.1. Решение уравненийСкачать

Решение основных алгебраических уравнений в октаве

Функция корней используется для решения алгебраических уравнений в Octave, и вы можете написать приведенные выше примеры следующим образом:

Например, давайте решим для х в уравнении х-5 = 0

Octave выполнит приведенный выше оператор и вернет следующий результат —

Вы также можете вызвать функцию решения как —

Octave выполнит приведенный выше оператор и вернет следующий результат —

Видео:2 13 Решение матричного уравнения AXB=CСкачать

Решение квадратичных уравнений в MATLAB

Функция решения также может решать уравнения более высокого порядка. Он часто используется для решения квадратных уравнений. Функция возвращает корни уравнения в массиве.

В следующем примере решается квадратное уравнение x 2 -7x +12 = 0. Создайте файл сценария и введите следующий код —

Когда вы запускаете файл, он показывает следующий результат —

Видео:Семинар 7. Символьные преобразования в MATLAB. 01.04.2021Скачать

Решение квадратичных уравнений в октаве

В следующем примере решается квадратное уравнение x 2 -7x +12 = 0 в октаве. Создайте файл сценария и введите следующий код —

Когда вы запускаете файл, он показывает следующий результат —

Видео:Решение системы нелинейных уравнений. Урок 139Скачать

Решение уравнений высшего порядка в MATLAB

Функция решения также может решать уравнения более высокого порядка. Например, давайте решим кубическое уравнение как (x-3) 2 (x-7) = 0

MATLAB выполнит приведенный выше оператор и вернет следующий результат —

В случае уравнений более высокого порядка корни длинные, содержащие много членов. Вы можете получить числовое значение таких корней, преобразовав их в двойные. В следующем примере решается уравнение четвертого порядка x 4 — 7x 3 + 3x 2 — 5x + 9 = 0.

Создайте файл сценария и введите следующий код —

Когда вы запускаете файл, он возвращает следующий результат —

Обратите внимание, что последние два корня являются комплексными числами.

Видео:Математика без Ху!ни. Метод Гаусса.Скачать

Решение уравнений высшего порядка в октаве

В следующем примере решается уравнение четвертого порядка x 4 — 7x 3 + 3x 2 — 5x + 9 = 0.

Создайте файл сценария и введите следующий код —

Когда вы запускаете файл, он возвращает следующий результат —

Решение системы уравнений в MATLAB

Функция решения также может быть использована для генерации решений систем уравнений, включающих более одной переменной. Давайте рассмотрим простой пример, чтобы продемонстрировать это использование.

Давайте решим уравнения —

Создайте файл сценария и введите следующий код —

Когда вы запускаете файл, он показывает следующий результат —

Таким же образом вы можете решать большие линейные системы. Рассмотрим следующую систему уравнений —

Решающая система уравнений в октаве

У нас есть немного другой подход к решению системы ‘n’ линейных уравнений с ‘n’ неизвестными. Давайте рассмотрим простой пример, чтобы продемонстрировать это использование.

Давайте решим уравнения —

Такая система линейных уравнений может быть записана в виде единого матричного уравнения Ax = b, где A — матрица коэффициентов, b — вектор столбцов, содержащий правую часть линейных уравнений, а x — вектор столбцов, представляющий решение как показано в программе ниже —

Создайте файл сценария и введите следующий код —

Когда вы запускаете файл, он показывает следующий результат —

Таким же образом, вы можете решить большие линейные системы, как указано ниже —

Разложение и сбор уравнений в MATLAB

Функция расширения и сбора расширяет и собирает уравнение соответственно. Следующий пример демонстрирует понятия —

Когда вы работаете со многими символическими функциями, вы должны объявить, что ваши переменные являются символическими.

Создайте файл сценария и введите следующий код —

Когда вы запускаете файл, он показывает следующий результат —

Расширяя и собирая уравнения в октаве

Вам нужно иметь символьный пакет, который обеспечивает расширение и функцию сбора для расширения и сбора уравнения, соответственно. Следующий пример демонстрирует понятия —

Когда вы работаете со многими символическими функциями, вы должны объявить, что ваши переменные являются символическими, но у Octave другой подход к определению символических переменных. Обратите внимание на использование Sin и Cos , которые также определены в символической упаковке.

Создайте файл сценария и введите следующий код —

Когда вы запускаете файл, он показывает следующий результат —

Факторизация и упрощение алгебраических выражений

Факторная функция разлагает выражение, а функция упрощения упрощает выражение. Следующий пример демонстрирует концепцию —

пример

Создайте файл сценария и введите следующий код —

Когда вы запускаете файл, он показывает следующий результат —