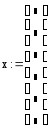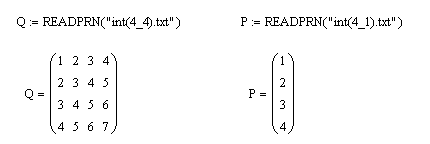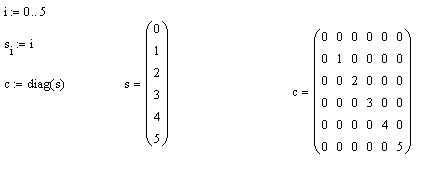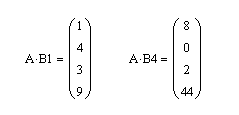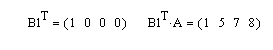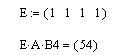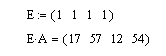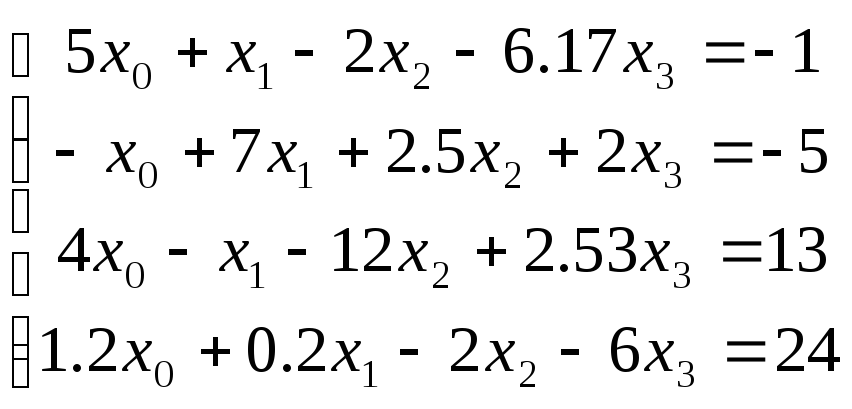Решение матричных уравнений в маткаде

Видео:MathCAD Решение системы линейных уравнений матричным методомСкачать

Лекція№9 — Операции с векторами и матрицами, матричные функции в математическом пакете MathCad

Матричное исчисление играет важную роль в компьютерной математике. Практически все численные методы на том или ином этапе работы своего алгоритма сводятся к решению систем линейных алгебраических уравнений (СЛАУ), которое часто производится матричными методами. Вообще говоря, нельзя назвать ни одной области использования компьютера, в алгоритмах которой (в большей или меньшей степени) не использовались бы матрицы.

Понятие «вектор» обычно не отделяют от понятия «матриц». Векторы могут рассматриваться как матрицы, состоящие из одного столбца (или строки).

Матричные вычисления в MathCAD можно условно разделить на три основных типа.

К первому относятся такие элементарные действия над матрицами, как создание, извлечение из них данных, их умножение, сложение или скалярное произведение (в случае векторов). Для их реализации служат специальные операторы трех панелей семейства Math (Математические): Calculator (Калькулятор), Matrix (Матричные) иSymbolics (Символьные).

Ко второму типу можно отнести те матричные преобразования, которые требуют использования специальных функций и встроенных алгоритмов матричной алгебры, таких как, например, функции вычисления определителя, матричных норм или сортировки элементов векторов по возрастанию. Функции этой группы можно найти в категории Vector and Matrix (Векторные и матричные) у мастера функций.

И, наконец, к третьему типу матричных вычислений следует отнести те задачи, решить которые можно только используя возможности системы программирования MathCAD.

В языках программирования начальные индексы массивов обычно равняются 0. По умолчанию в MathCAD индексы строк и столбцов также отсчитываются с 0. В том случае, если такая система вам неудобна или непривычна, можно изменить точку отсчета индексов на 1, задав системную переменную ORIGIN: ORIGIN:= 1.

Доступ к элементам вектора или матрицы осуществляется с помощью индексированных переменных. Например, чтобы использовать пятый элемент вектора с именем А, нужно записать этот элемент в виде: . А для того, чтобы взять элемент матрицы В, расположенный на пересечении 3-ей строчки и 4-го столбца нужно записать: .

Для задания индексов на панели Matrix предусмотрена специальная кнопка Subscript (Индекс). Перейти к записи индекса можно также с помощью клавиши «[» ( левая квадратная скобка). Нажав ее, вы увидите, что на месте будущего индекса, чуть ниже текста имени матрицы, появится черный маркер. В него через запятую следует ввести значения индексов. На первом месте при этом должен стоять номер строки, а на втором – столбца.

Видео:MathCAD решение матричного уравнения 1.wmvСкачать

3.1. Создание векторов и матриц

В системе предусмотрены различные возможности задания векторов и матриц:

Определение матрицы последовательным заданием каждого элемента.

С помощью индексированных переменных.

С помощью использования команды Insert→Matrix, либо с помощью соответствующей кнопки панели Matrix.

Задание с помощью элементов программирования.

Применение встроенных функций.

Через связь с другим приложением, например Excel.

Создание таблицы данных.

Чтение из внешнего файла.

Рассмотрим некоторые из них. Определение матрицы последовательным заданием каждого элемента очевидно и не требует пояснений. При создании матрицы или вектора с помощью индексированной переменной следует исходить из того, что любая индексированная переменная, индексами которой являются переменные, принимающие целочисленные значения из некоторого промежутка, уже представляют собой вектор или матрицу.

Пример 1. Требуется сформировать вектор x, состоящий из 6 элементов. Элементам этого вектора присвоить значения индексов.

Решение. Предоставим два варианта решения этой задачи:

с помощью индексированной переменной;

с помощью команды Insert→Matrix.

Вариант а

Для того, чтобы сформировать вектор, воспользуемся вспомогательной переменной, которая будет играть роль индекса (например, i), а затем будем использовать эту переменную для здания элементных значений вектора x. Формирование вектора представлено на рис. 3.1.

Рис. 3.1. Формирование вектора с использованием индексированной переменной

Вариант b

Формирование вектора х будем производить с помощью команды Matrix. Для этого сначала напишем оператор присваивания: «х:=» , а затем выполним команду Matrix. Эта команда открывает диалоговое окно«Insert Matrix», которое представлено на рис. 3.2, в котором необходимо указать число строк и число столбцов. В нашем примере число строк равно 6, а число столбцов равно 1.

После нажатия кнопки «Ok» команда предоставит шаблон с шестью ячейками, в которые следует вписать значения элементов вектора.

Рис. 3.2. Вызов диалогового окна «Insert Matrix» для создания матрицы с помощью команды «Matrix»

Пример 2. В файле с именем «int(4_4).txt» записаны числа в виде матрицы четыре строчки по четыре элемента, разделенными пробелами. В файле с именем «int(4_1).txt» записаны числа в столбик. Требуется прочитать эти данные в матрицу Q и вектор P.

Решение. Для чтения данных из файла в матрицу/вектор можно воспользоваться функцией READPRN, которая имеет один параметр — имя файла. Фрагмент с решением представлен на рис. 3.3.

Рис. 3.3. Чтение данных из файлов

С матрицами могут производиться как численные, так и символьные вычисления. Операции с матрицами в системе MathCAD обозначаются так, как это принято в математике: —, +, *, … .

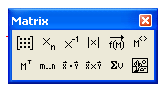
На рис. 3.4 показано назначение некоторых специализированных команд, расположенных на панели инструментов Matrix.

Помимо этого, система MathCAD представляет большое количество функций для работы с векторами и матрицами. Воспользоваться этими функциями можно с помощью мастера функций f(x).

Х -1 – получить обратную матрицу

|X| – вычислить детерминант

М Т – транспонировать

М – из матрицы взять вектор-столбец

v – получить сумму элементов

–скалярное произведение векторов

–векторное произведение векторов

Рис. 3.4. Назначение некоторых команд, расположенных на панели инструментов «Matrix»

На рис. 3.5 представлены вычисления с использованием операций над матрицами.

Рис. 3.5. Примеры матричных вычислений в MathCAD

Пример 3. Требуется сформировать диагональную квадратную матрицу с(6×6). Значения элементов главной диагонали должны совпадать с номером строки/столбца.

Решение. Для получения диагональной матрицы в системе предусмотрена функция diag, которая имеет один параметр – вектор диагональных элементов. Поэтому формирование матрицы начнем с создания вспомогательного вектора, в который занесем элементы для диагонали. Для формирования этого вспомогательного вектора (например, с именем s), воспользуемся вспомогательной переменной, которая будет играть роль индекса (например, i). Тогда формирование диагональной матрицы может быть получено в результате операций, как это показано на рис. 3.6.

Рис. 3.6. Формирование диагональной матрицы

Пример 4. Даны две матрицы: А(4×3) и В(4×2). Требуется объединить эти матрицы в одну матрицу С(4×5), причем, первыми столбцами новой матрицы должны быть столбцы матрицы А, а справа от этих элементов следовать столбцы матрицы В (методом «дописывания справа»).

Решение. Для соединения двух матриц в одну матрицу можно использовать функцию augment, параметрами которой будут являться имена соединяемых матриц, как это показано на рис. 7.7.

Рис. 3.7. Объединения двух матриц по правилу «дописывания справа»

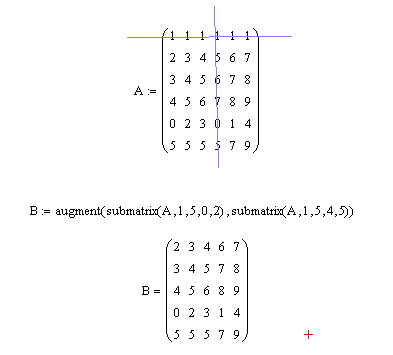
Пример 5. Даны две матрицы: А(2×3) и В(3×3). Требуется объединить эти матрицы в одну матрицу С(5×3), причем, в новой матрицы в качестве первых строк должны быть строки матрицы А, а за ними должны следовать строки матрицы В.

Решение. Для соединения двух матриц в одну матрицу по правилу «друг под другом» можно использовать функцию stack, параметрами которой будут являться имена соединяемых матриц, как это показано на рис. 3.8.

Рис. 3.8. Объединения двух матриц по правилу «друг под другом»

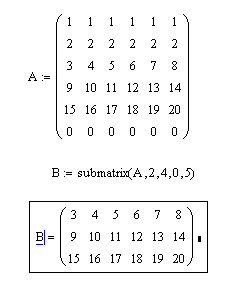
Пример 6. Дана матрица А(6×6). Требуется получить из этой матрицу подматрицу, в которую включить элементы, расположенные в строках, начиная с номера 2-го по номер 4-ый, и столбцах, начиная с номера 0-го по номер 5-ый.

Решение. Для выделения подматрицы с номерами столбцов и строк представленными граничными значениями предусмотрена функция submatrix. Эта функция имеет 5 параметров: имя матрицы, из которой производится выбор; начальный номер строки выбора; конечный номер строки выбора; начальный номер столбца выбора; конечный номер столбца выбора. Возможное решение представлено на рис. 3.9.

Рис. 3.9. Выделение подматрицы из заданной матрицы

Пример 7. Дана матрица А(6×6). Требуется получить из этой матрицу два вектора. Первый вектор должен совпадать с 4–ым столбцом матрицы А, а второй – с 3-ей строкой матрицы А.

Решение. Для получения векторных значений можно воспользоваться командой М (из матрицы взять вектор-столбец), которая расположена на панели «Мatrix». Для получения первого вектора эту команду нужно применить непосредственно к матрице А, а для получения второго вектора нужно сначала получить из матрицы Атранспонированную матрицу, а только потом воспользоваться командой «взять столбец». Возможное решение представлено на рис. 3.10.

Рис. 3.10. Выделение векторных значений из заданной матрицы

Пример 8. Из матрицы А(6×6) выделить минор, который образуется в результате вычеркивания из этой матрицы нулевой строчки и третьего столбца.

Решение. Решение задачи можно свести к соединению двух подматриц, выделенных из матрицы А, как это показано на рис. 3.11.

Рис. 3.11. Выделение минора из заданной матрицы

Видео:MathCAD решение матричного уравнения 2Скачать

3.2. Использование матриц специального вида для выполнения матричных операций в системе MathCad

Известно, что в результате умножении матрицы на вектор получается вектор. Причем, каждый i–ый элемент этого вектора-результата представляет собой сумму попарных произведений соответствующих элементов i–ой строки матрицы на элементы вектора-сомножителя. Очевидно, если в векторе, на который умножается матрица, все элементы равны нулю, а один элемент равен единице, то результатом такого произведения будет число, соответствующее тому элементуi–ой строки матрицы, где векторным сомножителем будет единица. Такой вывод можно использовать для выделения (формирования) из матрицы нужного столбца.

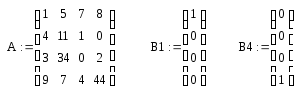
Пример 9. Даны матрица: А(4×4). Требуется получить из этой матрицу два вектора. Первый вектор должен совпадать с 0–ым столбцом матрицы А, а второй — с 3-им столбцом матрицы А.

Решение. Для получения новых векторов сформируем два вспомогательных вектора: вектор B1 – с единичным значением в строке с номером 0, а второй вектор В4 – с единичным значением в строке с номером 3. Тогда для получения векторов в соответствии с условием задачи достаточно умножить матрицу А справа на векторы В1 и В2, как это показано на рис. 3.12.

Рис. 3.12. Выделение векторных значений из заданной матрицы

Аналогичным образом можно получить вектор-строку из матрицы. Для этого достаточно сформировать вспомогательный вектор — строку, у которой все компоненты равны нулю, а одна компонента, номер которой соответствует номеру выделяемой строки из матрицы, равна единице. Если этот вектор умножить слева на матрицу, то в результате будет получена нужная строка.

Пример 10. Дана матрица: А(4×4). Требуется выделить из матрицы первую строку по порядку (с номером 0).

Решение. Сначала требуется подготовить вспомогательный вектор-строку, а потом умножить эту строку слева на матрицу А. Вектор-строку можно получить из предыдущего примера транспонированием вектора-столбца В1.

Такой прием можно использовать для перестановки строк и столбцов матрицы, только для этого потребуется уже вспомогательная матрица, состоящая из векторов-столбцов (векторов-строк), место единичных элементы которых соответствуют тому порядку, который нужно иметь в результате преобразования матрицы.

Пример 11. Дана матрица: А(4×4). Требуется переставить в матрице строки с номерами 0 и 1.

Решение. Для преобразования исходной матрицы требуется подготовить вспомогательную матрицу. Во вспомогательной матрице местоположение единиц в строках должно соответствовать нужному порядку для расположения строк в новой матрице. После этого решение можно получить простым перемножением матриц:

Пример 12. Дана матрица: А(4×4). Требуется переставить в матрице столбцы с номерами 0 и 1.

Решение. Для преобразования исходной матрицы требуется подготовить вспомогательную матрицу. Во вспомогательной матрице местоположение единиц в столбцах соответствуют нужному порядку для выбора их в новую матрицу. После этого решение можно получить простым перемножением матриц:

Рассуждая, таким образом, можно с помощью вспомогательного вектора с единичными компонентами получить вектор, компоненты которого будут равны сумме строк (столбцов) матрицы, а также суммы отдельно выделенного столбика (строчки).

Пример 13. Дана матрица: А(4×4). Требуется найти сумму элементов в столбце с номером 3.

Решение. Для решения задачи требуется подготовить вспомогательный вектор-строку из единичных элементов и выполнить умножение:

Пример 14. Дана матрица: А(4×4). Требуется получить вектора, элементы которого будут представлять суммы элементов в столбцах матрицы.

Решение. Для решения требуется подготовить вспомогательный вектор-строку из единичных элементов и выполнить умножение:

Видео:Решение систем линейных уравнений в MathCAD 14 (31/34)Скачать

3.3. Решение систем линейных алгебраических уравнений с использованием матричных преобразований

Для простоты решения ограничимся случаем системы из трех линейных уравнений с тремя неизвестными. Рассуждения на случай большего числа уравнений можно провести аналогичным образом. Пусть требуется найти решение система линейных алгебраических уравнений (СЛАУ) вида:

(3.1)

Введем следующие обозначения:

, (3.2)

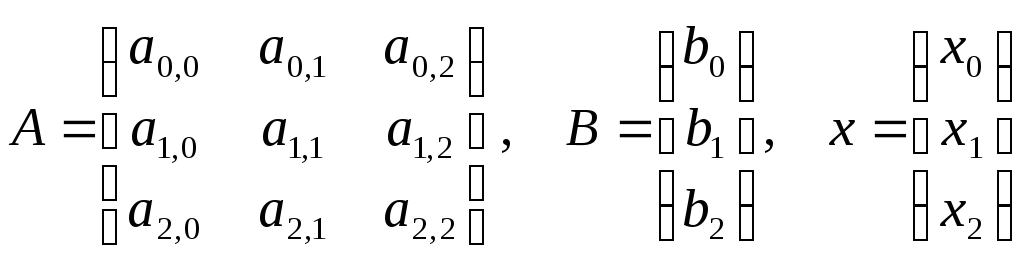
А – матрица коэффициентов;

В – вектор свободных членов;

х – вектор неизвестных.

В обозначениях (5.2) систему уравнений (5.1) можно записать в виде:

Из линейной алгебры известно, что система (3.3) имеет единственное решение при условии невырожденности матрицы, т.е. её детерминант должен быть отличным от нуля. Поэтому, какой бы вычислительный метод не применялся, решение системы линейных уравнений всегда нужно начинать с вычисления определителя (детерминанта) матрицы.

В разделе 6.4 мы уже рассматривали решение систем с использованием блока решения. Если применить к уравнению (3.3) аппарат матричных преобразований можно получить «матричную» формулу для вычисления x:

Помножим уравнение (3.3) слева на матрицу, обратную к матрице А:

. (3.4)

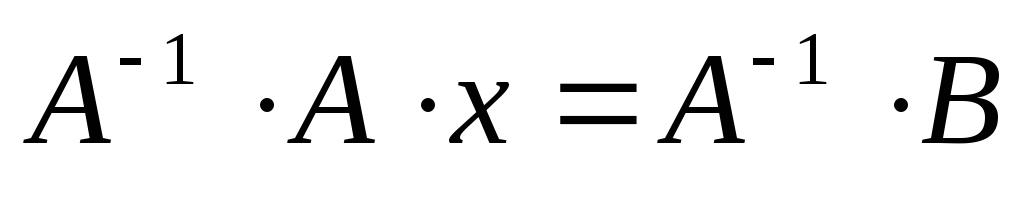
Воспользуемся свойством, что , гдеЕ – единичная матрица. Тогда уравнение (3.4) примет вид:

. (3.5)

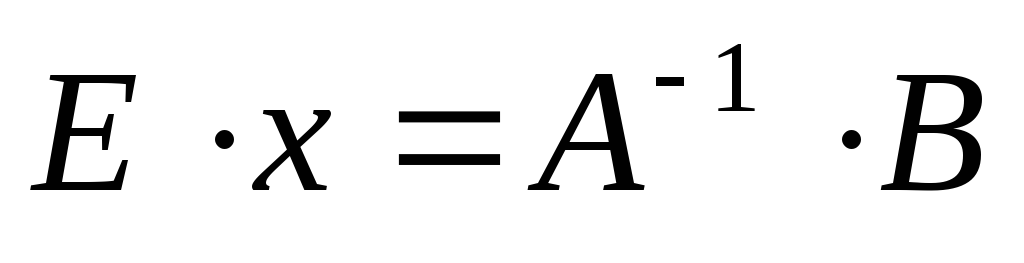
Воспользуемся свойством, что Ex = x. Тогда уравнение (3.5) примет вид:

, (3.6)

где (3.6) – решение системы (3.3).

Пример 15. Требуется найти решение следующей системы линейных уравнений:

Решение. Решение СЛАУ матричным способом в системе MathCAD приведено на рис.3.13.

Видео:Mathcad-09. Пример: уравненияСкачать

Решение матричных уравнений в маткаде

Видео:Решение матричных уравненийСкачать

Mathcad для студентов

Видео:MathCAD решение матричного уравнения 3.wmvСкачать

Mathcad для начинающих

Видео:Матрицы в Mathcad(создание и редактирование матриц)(Урок 3.1)Скачать

Скачать программы бесплатно

Видео:Решение СЛАУ в пакете MathCadСкачать

Решение системы линейных алгебраических уравнений матричным способом в Mathcad

Рассмотрим системы линейных алгебраических уравнений в Mathcad в векторно-матричной форме A*x =b, где А – квадратная матрица коэффициентов при неизвестных, причем определитель матрицы должен быть отличным от нуля; х- вектор неизвестных; b — вектор свободных членов. Решение данной сводится к следующему. Если определитель матрицы А отличен от нуля, то матрица А обратима. Тогда, умножив левую и правую часть и сходного уравнения на обратную матрицу (А-1), получаем решение в виде x=A-1*b. Реализовать полученное решение средствами Mathcad не представляет сложностей. Для случая бесконечного множества решений получаем сингулярную матрицу, Mathcad выдает сообщение “Matrix is singular. Cannot compute its inversу – Матрица сингулярная. Нельзя вычислить эту инверсию” и прерывает вычисления. На листинге представлен пример решения систем линейных алгебраических уравнений.

Видео:§29 Решение матричного уравненияСкачать

Решение системы линейных алгебраических уравнений методом Крамера в Mathcad

В Mathcad метод Крамера также предназначен для решения системы n линейных уравнений с n неизвестными вида A*x =b на основе предварительного вычисления определителей системы, при условии, что определитель матрицы А отличен от нуля. Метод основан на формулах Крамера, вида , где – определитель матрицы, полученной из матрицы А системы заменой i –го столбца, т.е. столбца коэффициентов при неизвестном Xi вектором свободных членов, т.е. b. На листинге в Mathcad приведен пример решения системы линейных алгебраических уравнений методом Крамера.

Видео:Ключевое слово solve в MathCAD 14 (26/34)Скачать

Матрицы и векторы в Mathcad

Операции, выполняемые над векторами и матрицами в Mathcad, можно разбить на две большие группы. К первой группе относятся операции, которые применяются к отдельным векторам и матрицами. Например, транспонирование матрицы или вычисление обратной матрицы в Mathcad. Ко второй группе относятся операции, которые выполняются над группой векторов и матриц. Как правило, они выполняются над двумя матрицами или матрицей и вектором. Например, сложение, вычитание матриц, перемножение матриц или умножение матрицы и вектора. К векторам и матрицам в Mathcad, при выполнении операций над ними, могут предъявляться определенные требования в соответствии с требованиями классической математики. Например, при перемножении матрицы и вектора, количество столбцов матрицы должно быть равно количеству срок вектора. Поэтому при работе с векторами и матрицами пользователь должен иметь необходимую математическую подготовку. В таблице приведены основные операции, выполняемые над векторами и матрицами, используемые в Mathcad. В таблице приняты следующие обозначение: А – массив, под которым понимается вектор или матрица, М – матрица, z — скаляр, v – вектор.

Наиболее удобно выполнять матричные вычисления с использованием кнопок панели инструментов “Матрица”. По умолчанию индексация строк и столбцов элементов матрицы начинается с 0. Для того чтобы индексация начиналась с 1, необходимо системной переменной ORIGIN присвоить значение 1. На листинге приведен пример матричных вычислений в Mathсad.

Видео:Лекция 8. Решение матричных уравненийСкачать

Матричные функции в Mathcad

Mathсad имеет более 50 функций, предназначенных для работы с векторами и матрицами. Все функции можно разбить на группы по их функциональному назначению. Например, функции, предназначенные для создания матриц общего и специального вида, редактирования и преобразования матриц, функции, определяющие параметры матриц и т. д. Рассмотрим часть этих функций, которые имеют наибольшее прикладное значение.

Среди функций, предназначенных для создания матриц, следует выделить функцию matrix(L,N,f), где L – число строк матрицы, N – число столбцов матрицы, f – функция f(l,n) при . Другая функция из этой группы identity(n). Функция предназначена для создания единичной матрицы размерности n. Следующая функция geninv(M) позволяет осуществить обращение матрицы M, аналогично операции M -1 .

Для определения размерности матрицы в Mathcad предназначены функция rows(M), определяющая число строк матрицы M, и функция cols(M), определяющая число колонок матрицы M.

Сортировку элементов матрицы осуществляют две функции csort(M,i), rsort(M,j). Функция csort(M,i) обеспечивает сортировку по возрастанию элементов i – го столбца путем перестановки строк, а функция rsort(M,j) – сортировку по возрастанию элементов j –ой строки путем перестановки столбцов.

Для определения минимального и максимального элемента матрицы используются функции min(M) и max(M).

Выделить произвольную подматрицу из матрицы М в Mathcad можно посредством функции submatrix (M, r1, r2, c1, c2), где М – исходная матрица, r1 и r2 –нижний и верхний номер строки матрицы М, включаемых в результирующую подматрицу, а с1 и с2 – нижней и верхний номер столбца матрицы М, включаемых в результирующую подматрицу. Слияние матриц можно осуществить, используя функции augment(A,B,…) и stack(A,B,…). Функция augment(A,B,…) предназначена для слияния матриц А, В и т.д. слева направо. Причем количество строк в матрицах должно быть одинаково. Вторая функция stack(A,B,…) выполняет слияние матриц сверху вниз. Количество столбцов в матрицах должно быть также одинаково. Данные функции могут быть применены и к векторам. На листинге приведен пример использования рассмотренных матричных функций.

Видео:MathCAD Решение уравнений с помощью функции root 1 вариантСкачать

Матричные вычисления в Mathcad

Создание векторов и матриц реализовано в Mathсad различными способами. В данном разделе рассматриваются только функции и операции с векторами и матрицами, а так же прикладное использование векторов и матриц для решения некоторых задач.

Матричные функции

В Mathсad очень много функций, предназначенных для работы с матрицами и векторами.

Основные операции с матрицами и векторами

Операции, выполняемые над векторами и матрицами, можно разбить на разные большие группы.

Решение системы линейных алгебраических уравнений матричным способом

В Mathcad можно решать системы линейных алгебраических уравнений матричным способом.

Решение системы линейных алгебраических уравнений методом Крамера

Также предназначен метод Крамера для решения системы n линейных уравнений с n неизвестными.

🎬 Видео

Числовое решение. Функция polyroots в MathCAD 14 (27/34)Скачать

MathCAD Решение системы уравненийСкачать

Пример решения уравнения в MathCAD 14 (33/34)Скачать

Mathcad Prime (часть 2)Скачать

MathCAD. Given - FindСкачать