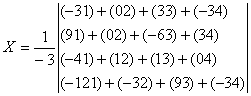Напомним, что решением системы линейных уравнений называется всякая совокупность чисел <x1, x2, . xn> , подстановка которых в эту систему вместо соответствующих неизвестных обращает каждое уравнение системы в тождество.
Система линейных алгебраических уравнений обычно записывается как (для 3-х переменных):
| 2x1-3x2+x3 = 4 -x1+2x2+5x3 = 10 3x1-x2+3x3 = -1 | или | 2x-3y+z = 4 -z+2y+5z = 10 3x-y+3z = -1 |
См. также Решение матричных уравнений.</x
- Алгоритм решения
- Матричный метод решения СЛАУ: пример решения с помощью обратной матрицы
- Пример решения системы линейных уравнений с помощью метода обратной матрицы
- Матричный метод онлайн
- Предупреждение
- Матричный метод решения систем линейных уравнений
- Примеры решения системы линейных уравнений матричным методом
- 🎥 Видео
Видео:Решение матричных уравненийСкачать
Алгоритм решения
- Вычисляется определитель матрицы A . Если определитель равен нулю, то конец решения. Система имеет бесконечное множество решений.
- При определителе отличном от нуля, через алгебраические дополнения находится обратная матрица A -1 .
- Вектор решения X =<x1, x2, . xn> получается умножением обратной матрицы на вектор результата B .
Пример №1 . Найти решение системы матричным методом. Запишем матрицу в виде:
|
Вектор B:
B T = (3,-2,-1)
Система будет иметь решение, если определитель матрицы A отличен от нуля.
Найдем главный определитель.
∆ = 2•(1•(-2)-2•0)-(-2•(3•(-2)-2•1))+1•(3•0-1•1) = -21
Итак, определитель -21 ≠ 0, поэтому продолжаем решение. Для этого найдем обратную матрицу через алгебраические дополнения.
Транспонированная матрица
| A T = |
|
Алгебраические дополнения.
| A1,1 = (-1) 1+1 |
| ∆1,1 = (1•(-2)-0•2) = -2 |
| A1,2 = (-1) 1+2 |
| ∆1,2 = -(3•(-2)-1•2) = 8 |
| A1,3 = (-1) 1+3 |
| ∆1,3 = (3•0-1•1) = -1 |
| A2,1 = (-1) 2+1 |
| ∆2,1 = -(-2•(-2)-0•1) = -4 |
| A2,2 = (-1) 2+2 |
| ∆2,2 = (2•(-2)-1•1) = -5 |
| A2,3 = (-1) 2+3 |
| ∆2,3 = -(2•0-1•(-2)) = -2 |
| A3,1 = (-1) 3+1 |
| ∆3,1 = (-2•2-1•1) = -5 |
| A3,2 = (-1) 3+2 |
| ∆3,2 = -(2•2-3•1) = -1 |
| A3,3 = (-1) 3+3 |
| ∆3,3 = (2•1-3•(-2)) = 8 |
Обратная матрица:
| A -1 = -1/21 |
|
Вектор результатов X = A -1 • B
|
X T = (1,0,1)
x1 = -21 / -21 = 1
x2 = 0 / -21 = 0
x3 = -21 / -21 = 1
Проверка:
2•1+3•0+1•1 = 3
-2•1+1•0+0•1 = -2
1•1+2•0+-2•1 = -1
Запишем матрицу в виде:
Вектор B:
B T = (1,2,3,4)
Главный определитель
Минор для (1,1):
= 3•(3•2-6•2)-5•(3•2-6•1)+7•(3•2-3•1) = 3
Определитель минора
∆ = 2•(-3)-3•0+5•3-4•3 = -3
Вектор результатов X
X = A -1 ∙ B
Пример №3 . Систему уравнений записать в матричной форме и решить ее с помощью обратной матрицы. Сделать проверку полученного решения.
Решение:xls
Пример №4 . Записать систему уравнений в матричной форме и решить с помощью обратной матрицы.
Решение:xls
Пример №5 . Дана система трех линейных уравнений с тремя неизвестными. Требуется: 1) найти ее решение с помощью формул Крамера; 2) записать систему в матричной форме и решить ее средствами матричного исчисления.
Методические рекомендации. После решения методом Крамера, найдите кнопку «Решение методом обратной матрицы для исходных данных». Вы получите соответствующее решение. Таким образом, данные вновь заполнять не придется.
Решение. Обозначим через А — матрицу коэффициентов при неизвестных; X — матрицу-столбец неизвестных; B — матрицу-столбец свободных членов:
|
Вектор B:
B T =(4,-3,-3)
С учетом этих обозначений данная система уравнений принимает следующую матричную форму: А*Х = B.
Если матрица А — невырожденная (ее определитель отличен от нуля, то она имеет обратную матрицу А -1 . Умножив обе части уравнения на А -1 , получим: А -1 *А*Х = А -1 *B, А -1 *А=Е.
Это равенство называется матричной записью решения системы линейных уравнений. Для нахождения решения системы уравнений необходимо вычислить обратную матрицу А -1 .
Система будет иметь решение, если определитель матрицы A отличен от нуля.
Найдем главный определитель.
∆=-1•(-2•(-1)-1•1)-3•(3•(-1)-1•0)+2•(3•1-(-2•0))=14
Итак, определитель 14 ≠ 0, поэтому продолжаем решение. Для этого найдем обратную матрицу через алгебраические дополнения.
Пусть имеем невырожденную матрицу А:
| A= |
|
Тогда:
| A=1/∆ |
|
где Aij — алгебраическое дополнение элемента aij в определителе матрицы А, которое является произведением (—1) i+j на минор (определитель) n-1 порядка, полученный вычеркиванием i-й строки и j-го столбца в определителе матрицы А.
Транспонированная матрица
| A T = |
|
Вычисляем алгебраические дополнения.
| A1,1=(-1) 1+1 |
|
∆1,1=(-2•(-1)-1•1)=1
| A1,2=(-1) 1+2 |
|
∆1,2=-(3•(-1)-0•1)=3
| A1,3=(-1) 1+3 |
|
∆1,3=(3•1-0•(-2))=3
| A2,1=(-1) 2+1 |
|
∆2,1=-(3•(-1)-1•2)=5
| A2,2=(-1) 2+2 |
|
∆2,2=(-1•(-1)-0•2)=1
| A2,3=(-1) 2+3 |
|
∆2,3=-(-1•1-0•3)=1
| A3,1=(-1) 3+1 |
|
∆3,1=(3•1-(-2•2))=7
| A3,2=(-1) 3+2 |
|
∆3,2=-(-1•1-3•2)=7
| A3,3=(-1) 3+3 |
|
∆3,3=(-1•(-2)-3•3)=-7
Обратная матрица
| A -1 =1/14 |
|
Вектор результатов X
X=A -1 • B
|
| X=1/14 |
|
| X=1/14 |
|
X T =(-1,1,2)
x1= -14 / 14=-1
x2= 14 / 14=1
x3= 28 / 14=2
Проверка.
-1•-1+3•1+0•2=4
3•-1+-2•1+1•2=-3
2•-1+1•1+-1•2=-3
doc:xls
Ответ: -1,1,2.
Пример №6 . Решить неоднородную систему линейных алгебраических уравнений методом обратной матрицы.
Видео:Решение системы уравнений методом обратной матрицы - bezbotvyСкачать
Матричный метод решения СЛАУ: пример решения с помощью обратной матрицы
В данной статье мы расскажем о матричном методе решения системы линейных алгебраических уравнений, найдем его определение и приведем примеры решения.
Метод обратной матрицы — это метод, использующийся при решении СЛАУ в том случае, если число неизвестных равняется числу уравнений.
Найти решение системы n линейных уравнений с n неизвестными:
a 11 x 1 + a 12 x 2 + . . . + a 1 n x n = b 1 a n 1 x 1 + a n 2 x 2 + . . . + a n n x n = b n
Матричный вид записи: А × X = B
где А = а 11 а 12 ⋯ а 1 n а 21 а 22 ⋯ а 2 n ⋯ ⋯ ⋯ ⋯ а n 1 а n 2 ⋯ а n n — матрица системы.
X = x 1 x 2 ⋮ x n — столбец неизвестных,
B = b 1 b 2 ⋮ b n — столбец свободных коэффициентов.
Из уравнения, которое мы получили, необходимо выразить X . Для этого нужно умножить обе части матричного уравнения слева на A — 1 :
A — 1 × A × X = A — 1 × B .
Так как А — 1 × А = Е , то Е × X = А — 1 × В или X = А — 1 × В .
Обратная матрица к матрице А имеет право на существование только, если выполняется условие d e t A н е р а в е н н у л ю . Поэтому при решении СЛАУ методом обратной матрицы, в первую очередь находится d e t А .
В том случае, если d e t A н е р а в е н н у л ю , у системы имеется только один вариант решения: при помощи метода обратной матрицы. Если d e t А = 0 , то систему нельзя решить данным методом.
Видео:Решение системы уравнений методом обратной матрицы.Скачать
Пример решения системы линейных уравнений с помощью метода обратной матрицы
Решаем СЛАУ методом обратной матрицы:
2 x 1 — 4 x 2 + 3 x 3 = 1 x 1 — 2 x 2 + 4 x 3 = 3 3 x 1 — x 2 + 5 x 3 = 2
- Записываем систему в виде матричного уравнения А X = B , где
А = 2 — 4 3 1 — 2 4 3 — 1 5 , X = x 1 x 2 x 3 , B = 1 3 2 .
- Выражаем из этого уравнения X :
- Находим определитель матрицы А :
d e t A = 2 — 4 3 1 — 2 4 3 — 1 5 = 2 × ( — 2 ) × 5 + 3 × ( — 4 ) × 4 + 3 × ( — 1 ) × 1 — 3 × ( — 2 ) × 3 — — 1 × ( — 4 ) × 5 — 2 × 4 — ( — 1 ) = — 20 — 48 — 3 + 18 + 20 + 8 = — 25
d e t А не равняется 0, следовательно, для этой системы подходит метод решения обратной матрицей.
- Находим обратную матрицу А — 1 при помощи союзной матрицы. Вычисляем алгебраические дополнения А i j к соответствующим элементам матрицы А :
А 11 = ( — 1 ) ( 1 + 1 ) — 2 4 — 1 5 = — 10 + 4 = — 6 ,
А 12 = ( — 1 ) 1 + 2 1 4 3 5 = — ( 5 — 12 ) = 7 ,
А 13 = ( — 1 ) 1 + 3 1 — 2 3 — 1 = — 1 + 6 = 5 ,
А 21 = ( — 1 ) 2 + 1 — 4 3 — 1 5 = — ( — 20 + 3 ) = 17 ,
А 22 = ( — 1 ) 2 + 2 2 3 3 5 — 10 — 9 = 1 ,
А 23 = ( — 1 ) 2 + 3 2 — 4 3 — 1 = — ( — 2 + 12 ) = — 10 ,
А 31 = ( — 1 ) 3 + 1 — 4 3 — 2 4 = — 16 + 6 = — 10 ,
А 32 = ( — 1 ) 3 + 2 2 3 1 4 = — ( 8 — 3 ) = — 5 ,
А 33 = ( — 1 ) 3 + 3 2 — 4 1 — 2 = — 4 + 4 = 0 .
- Записываем союзную матрицу А * , которая составлена из алгебраических дополнений матрицы А :
А * = — 6 7 5 17 1 — 10 — 10 — 5 0
- Записываем обратную матрицу согласно формуле:
A — 1 = 1 d e t A ( A * ) T : А — 1 = — 1 25 — 6 17 — 10 7 1 — 5 5 — 10 0 ,
- Умножаем обратную матрицу А — 1 на столбец свободных членов В и получаем решение системы:
X = A — 1 × B = — 1 25 — 6 17 — 10 7 1 — 5 5 — 10 0 1 3 2 = — 1 25 — 6 + 51 — 20 7 + 3 — 10 5 — 30 + 0 = — 1 0 1
Ответ: x 1 = — 1 ; x 2 = 0 ; x 3 = 1
Видео:Матричный метод решения систем уравненийСкачать
Матричный метод онлайн
Данный онлайн калькулятор решает систему линейных уравнений матричным методом. Дается очень подробное решение. Для решения системы линейных уравнений выберите количество переменных. Выбирайте метод вычисления обратной матрицы. Затем введите данные в ячейки и нажимайте на кнопку «Вычислить».
Предупреждение
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Видео:9. Метод обратной матрицы для решения систем линейных уравнений / матричный методСкачать
Матричный метод решения систем линейных уравнений
Рассмотрим следующую систему линейных уравнений:
 | (1) |
Для решения системы линейных уравнений (1) матричным методом запишем ее матричном виде:
| Ax=b, | (2) |
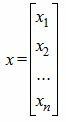   | (3) |
Мы будем предполагать, что матрица A имеет обратное, т.е. определитель матрицы A не равен нулю.
Умножим матричное уравнение (2) на обратную матрицу A −1 . Тогда
| A −1 Ax=A −1 b. | (4) |
Учитывая определение обратной матрицы, имеем A −1 A=E, где E— единичная матрица. Следовательно (4) можно записать так:
| Ex=A −1 b. | (4) |
или, учитывая, что Ex=x:
| x=A −1 b. | (5) |
Таким образом, для решения системы линейных уравнений (1) (или (2)), достаточно умножить обратную к A матрицу на вектор ограничений b.
Видео:Система линейных уравнений. Метод обратной матрицы. Матричный метод.Скачать
Примеры решения системы линейных уравнений матричным методом
Пример 1. Решить следующую систему линейных уравнений матричным методом:
 |
Матричный вид записи системы линейных уравнений: Ax=b, где
 . |
Найдем обратную к матрице A методом Жордана-Гаусса. С правой стороны матрицы A запишем единичную матрицу:
 . |
Выбираем самый большой по модулю ведущий элемент столбца 1. Для этого заменяем местами строки 1 и 2:
 . |
Исключим элементы 1-го столбца матрицы ниже главной диагонали. Для этого сложим строки 2,3 со строкой 1, умноженной на -1/3,-1/3 соответственно:
 . |
Выбираем самый большой по модулю ведущий элемент столбца 2. Для этого заменяем местами строки 2 и 3:
 . |
Исключим элементы 2-го столбца матрицы ниже главной диагонали. Для этого сложим строку 3 со строкой 2, умноженной на -24/51:
 . |
Исключим элементы 3-го столбца матрицы выше главной диагонали. Для этого сложим строки 1, 2 со строкой 3, умноженной на 17/53, 85/159 соответственно:
 . |
Исключим элементы 2-го столбца матрицы выше главной диагонали. Для этого сложим строку 1 со строкой 2, умноженной на -3/17:
 . |
Делим каждую строку матрицы на ведущий элемент соответствующей строки:
 . |
Отделяем правую часть матрицы. Полученная матрица является обратной матрицей к A :
 . |
Обратная матрица найдена. Решение системы линейных уравнений имеет вид x=A−1b. Тогда
  . |
 |
Пример 2. Решить следующую систему линейных уравнений матричным методом:
 . |
Матричный вид записи системы линейных уравнений: Ax=b, где
 . |
Найдем обратную к матрице A методом алгебраических дополнений. Вычислим определитель матрицы A :
 . |
Вычислим все алгебраические дополнения матрицы A:
 , |
 , |
 , |
 , |
 , |
 , |
 , |
 , |
 . |
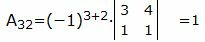Обратная матрица вычисляется из следующего выражения:
 |
где Aij − алгебраическое дополнение элемента матрицы A, находящиеся на пересечении i-ой строки и j-ого столбца, а Δ − определитель матрицы A.
Используя формулу обратной матрицы, получим:
  |
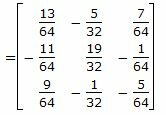Обратная матрица найдена. Решение системы линейных уравнений имеет вид x=A −1 b. Тогда
🎥 Видео
Обратная матрицаСкачать
Матричный метод решения систем линейных уравнений (метод обратной матрицы)Скачать
8. Обратная матрицаСкачать
Обратная матрица. Решение матричных уравненийСкачать
Как находить обратную матрицу - bezbotvyСкачать
Решение системы уравнений методом Крамера.Скачать
Урок 2. Обратная матрица: метод Гаусса, алгебраическое дополнение | Высшая математика | TutorOnlineСкачать
Матричные уравнения Полный разбор трех типов матричных уравненийСкачать
Обратная матрица (2 способа нахождения)Скачать
§29 Решение матричного уравненияСкачать
Лекция 3. Свойства алгебраических операций над матрицамиСкачать
Лекция 8. Решение матричных уравненийСкачать
Математика без Ху!ни. Метод Гаусса.Скачать
Линейная алгебра, 5 урок, Обратная матрицаСкачать
