Министерство образования и науки Республики Беларусь
Белорусский государственный университет
информатики и радиоэлектроники
Факультет информационных технологий и управления
Кафедра Вычислительных Методов и Программирования
к курсовой работе
«Решение системы линейных уравнений»
ст.гр.020603 Навроцкий А.А.
1. Анализ существующих методов решения задачи.
2. Описание используемого метода.
3. Анализ результатов.
Список использованной литературы.
Приложение (распечатка программы, результатов).
Решение систем линейных алгебраических уравнений (СЛАУ) является одной из основных задач линейной алгебры. Эта задача имеет важное прикладное значение при решении научных и технических проблем. Кроме того, является вспомогательной при реализации многих алгоритмов вычислительной математики, математической физики, обработки результатов экспериментальных исследований.
Применяемые на практике численные методы решения СЛАУ делятся на две группы — прямые и итерационные.
В прямых (или точных) методах решение системы получают за конечное число арифметических действий. К ним относятся известное правило Крамера нахождения решения с помощью определителей, метод последовательного исключения неизвестных (метод Гаусса) и его модификации, метод прогонки и другие. Сопоставление различных прямых методов проводится обычно по числу арифметический действий, необходимых для получения решения. Прямые методы являются универсальными и применяются для решения систем до порядка 10 3 . Отметим, что вследствие погрешностей округления при решении задач на ЭВМ прямые методы на самом деле не приводят к точному решению системы.
Итерационные (или приближенные) методы являются бесконечными и находят решение системы как предел при k®¥ последовательных приближений x ( k ) , где k — номер итерации. Обычно задается точность e, и вычисления проводятся до тех пор, пока не будет выполнена оценка ºx ( k ) – x ( k -1) º 2 числовым равенствам
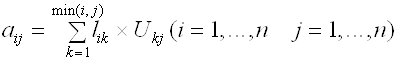
Разложение матрицы A на множители обычно получают посредством алгоритма, который называется компактной схемой метода Гаусса. Элементы lim и Umi могут быть вычислены по формулам
Тогда решение системы Ax=b сводится к последовательному решению двух систем — Ly=b и Ux=y.
Рассмотренный метод можно применять к решению серии систем с одной и той же матрицей.
Метод простых итераций (Якоби).
Для решения итерационным методом система линейных алгебраических уравнений Ax = b должна быть приведена к виду x = Gx+f , где G — некоторая матрица, f — преобразованный вектор свободных членов. Затем выбирается начальное приближение — произвольный вектор x (0) — и строится рекуррентная последовательность векторов x (1) , x (2) . x ( k ) . по формуле
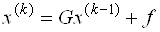
Для сходимости этой последовательности при любом начальном приближении необходимо и достаточно, чтобы все собственные значения матрицы G были по абсолютной величине меньше единицы. На практике это трудно проверить, и обычно пользуются достаточными условиями сходимости — итерации сходятся, если какая-нибудь норма матрицы меньше единицы, т.е.
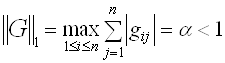
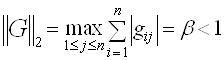
Чем меньше норма матрицы G, тем быстрее сходится итерационный процесс.
Преобразование системы можно осуществить, просто решая каждое i-е уравнение относительно xi :
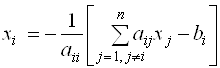
Метод Якоби использует следующий алгоритм построения приближений:
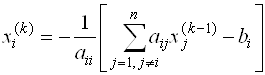
Если A — матрица с доминирующей диагональю, т.е. 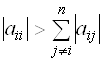
Метод Якоби относится к одношаговым итерационным методам, когда для нахождения x ( k +1) требуется помнить только одну предыдущую итерацию x ( k ) . Для исследования сходимости удобнее записывать итерационные методы не в координатной, а в матричной форме, придерживаясь стандартной формы записи итерационных методов.
Канонической формой одношагового итерационного метода решения СЛАУ называется его запись в виде
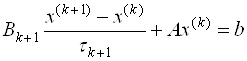
где Bk+1 — матрица, задающая тот или иной итерационный метод, tk+1 — итерационный параметр. Числовые параметры tk вводят для ускорения сходимости. Способ выбора итерационных параметров определяется при исследовании сходимости метода, когда выясняется при каких значениях параметров метод сходится и когда сходимость будет наиболее быстрой (соответствующие параметры называются оптимальными).
Итерационный метод называют явным, если Bk+1 — единичная матрица. Неявные итерационные методы имеет смысл применять лишь в том случае, когда решение системы уравнений с матрицей Bk требует меньше машинной памяти или времени или алгоритмически проще, чем решение исходной системы.
Методом простой итерации называют явный метод с постоянм параметром
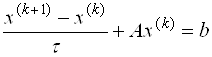
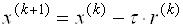
где r ( k ) = Ax ( k ) -b — вектор невязки. Метод сходится для симметричных положительно определенных матриц при 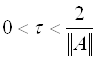
Для окончания итерационного процесса используют три способа. При первом определяют величину стабилизации и прекращают вычисления, если она меньше e, т.е.
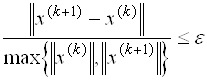
Недостатком этого способа является то, что при медленно сходящихся итерациях величина стабилизации может быть малой, хотя приближенное решение сильно отличается от точного.
При втором способе вычисляют нормы невязки до начала итераций и на каждой итерации. Итерации прекращают при выполнении неравенства
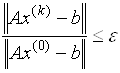
При третьем способе предварительно оценивается число итераций, необходимое для получения заданной точности e. Если для погрешности итерационного метода выполняются оценки
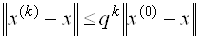
- Привет студент
- ПРОГРАММНАЯ РЕАЛИЗАЦИЯ РЕШЕНИЯ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ
- тема: «ПРОГРАММНАЯ РЕАЛИЗАЦИЯ РЕШЕНИЯ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ»
- Программирование решения уравнений
- Скачать:
- Подписи к слайдам:
- Предварительный просмотр:
- Предварительный просмотр:
- Паспорт проекта
- Индивидуальный план работы над проектом
- Отзыв
- Общие сведения о языке программирования Паскаль
- Решение системы алгебраических уравнений методом Гаусса
- Решение нелинейных уравнений
- Заключение
- Список литературы
- Текст публичного выступления
- 🎬 Видео
Видео:Метод Крамера за 3 минуты. Решение системы линейных уравнений - bezbotvyСкачать

Привет студент
ПРОГРАММНАЯ РЕАЛИЗАЦИЯ РЕШЕНИЯ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ
Приднестровский государственный университет им. Т.Г. Шевченко
Кафедра программного обеспечения вычислительной техники
и автоматизированных систем
КУРСОВАЯ РАБОТА
«Информатика и программирование»
Видео:Алгебра 7 класс (Урок№43 - Решение линейных уравнений с одним неизвестным.)Скачать

тема: «ПРОГРАММНАЯ РЕАЛИЗАЦИЯ РЕШЕНИЯ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ»
студентка группы ИТ13ДР62ИС1
Арабаджи Федор Иванович
ЗАДАНИЕ
на курсовую работу по дисциплине
«ПРОГРАММИРОВАНИЕ»
Студента группы ________ — ___________________
утверждена протоколом кафедры _________ № _____ от «____» ____________ 20___ г.
Цель курсовой работы:
Задачи курсовой работы:
Результаты курсовой работы:
График обязательных консультаций:
Дата сдачи записки на регистрацию «_____» __________20__ г.
Дата защиты курсовой работы «_____» __________20__ г.
Задание принял к исполнению «_____» __________20__ г. ___________/________________/
Руководитель работы ______________________ /________________/
СОДЕРЖАНИЕ
2 ОПИСАНИЕ ПРЕДМЕТНОЙ ОБЛАСТИ………………………………….
2.3 Метод обратной матрицы…………………………………………….
3 РУКОВОДСТВО ПРОГРАММИСТА………………………………………..
3.1 Введение и общие сведения……………………………………………
3.2 Структура программного продукта………………………………….
3.4 Описание исходных текстов программного продукта…………….
3.5 Аппаратная и программная часть…………………………………….
3.6 Результаты тестирования и опытной эксплуатации………………….
4 РУКОВОДСТВО ПОЛЬЗОВАТЕЛЯ……………………………………….
4.3 Установка программного продукта……………………………….…..
4.4 Запуск и работа с программным продуктом…………………….……
4.5 Удаление программного продукта…………………………………….
СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ…………………………….
Введение
Последние десятилетия характеризуются бурным развитием вычислительной техники. Расширяются области применения вычислительных машин и совершенствуются методы их использования. Созданы универсальные языки программирования и разработаны мощные операционные системы.
Сейчас невозможно представить себе какую-либо область деятельности, обходящуюся без применения компьютерной техники.
Компьютеры используются при проведении различных инженерных расчётов, при решении экономических задач, в процессе управления производством, при получении оценок производственных ситуаций и во многих других случаях.
Решение систем линейных алгебраических уравнений является одной из основных задач линейной алгебры. Эта задача имеет важное прикладное значение при решении научных и технических проблем. Кроме того, является вспомогательной при реализации многих алгоритмов вычислительной математики, математической физики, обработки результатов экспериментальных исследований.
Алгебраическое уравнение называется линейным, если оно содержит переменные только в первой степени и не содержит произведений переменных.
Решение систем линейных алгебраических уравнений является одной из фундаментальных задач математики. В частности, она возникает при решении краевых задач для дифференциальных и интегральных уравнений, к которым сводятся реальные проблемы техники, физики, экономики, математики и др. Подобные программы довольно популярны, в особенности среди пользователей глобальной сети Интернет. Они могут быть широко применимы в среде образовательных учреждений. Например, преподавателю необходимо проверить десятки работ студентов в короткий срок или составить варианты контрольных работ, помочь студенту в решении систем линейных уравнений и в их объяснении, так как программа будет содержать краткую теоретическую справку.
Чтобы быстро справится с решением системы линейных уравнений, можно воспользоваться средствами вычислительной техники – написать программу на языке программирования.
Учитывая современные возможности, можно облегчить процесс решения систем линейных уравнений. Данную задачу можно выполнить программно для упрощения и автоматизации процесса решения систем линейных уравнений методом Гаусса, методом Крамера, а также методом обратной матрицы с помощью Windows-приложения, реализованного средствами языка высокого уровня С#.
Данный продукт найдёт своё применение в сфере образования. В частности, например, учащиеся с помощью данной программы смогут проверить правильность решения систем линейных уравнений.
1 постановка задачи
В данной курсовой работе необходимо создать программный продукт при помощи Windows Forms на языке C#, который представлял бы возможность:
- ввода данных с клавиатуры или считывания их из файла с представлением права выбора пользователю;
- решения системы линейных уравнений;
- запись данных в файл;
- доступа к файлу, куда записываются входные и выходные данные.
Программа должна выполнять решение систем линейных уравнений методом Гаусса, методом Крамера или методом обратной матрицы.
Окно программы должно содержать:
- пункты меню: Файл, Правка, Примеры, Справка, О программе;
- поле выбора метода решения системы линейных уравнений;
- поле выбора количества уравнений в системе;
- поля для входных и выходных данных;
- кнопки операций.
Входными данными являются числа вещественного типа, введенные с клавиатуры или считанные из файла. Программа распознает входные данные и производит решение системы одним из выбранных методов.
Результатом работы программы служит отображение получившейся матрицы или определителя (в зависимости от выбранного способа) и корни системы уравнений, полученные в результате решения системы.
2 описание предметной области
Решение систем линейных алгебраических уравнений – одна из фундаментальных задач математики. Система m линейных алгебраических уравнений с n неизвестными (или, линейная система, также употребляется аббревиатура СЛАУ) в линейной алгебре — это система уравнений вида (Рисунок 1)
Рисунок 1- Система уравнений
В системе уравнений (Рисунок 1) m является количеством уравнений, а n – количество неизвестных. x1, x2, … xn – это неизвестные, которые надо определить. a11, a12, … amn – коэффициенты системы, а b1, b2, … bm – свободные члены. Индексы коэффициентов (aij) системы обозначают номера уравнения (i) и неизвестного (j), при котором стоит этот коэффициент, соответственно.
Существуют следующие способы решения систем линейных уравнений:
– метод обратной матрицы.
2.1 Метод Гаусса
Метод Гаусса – классический метод решения системы линейных алгебраических уравнений. Это метод последовательного исключения переменных, когда с помощью элементарных преобразований система уравнений приводится к равносильной системе треугольного вида, из которой последовательно, начиная с последних (по номеру), находятся все переменные системы. Хотя в настоящее время данный метод повсеместно называется методом Гаусса, он был известен и до К.Ф. Гаусса. Первое известное описание данного метода приведено в китайском трактате «Математика в девяти книгах», составленном между первым веком до н. э. и вторым веком н. э.
Далее приведено более подробное описание метода. Пусть исходная система будет вида (Рисунок 2):
Рисунок 2 — Исходная система уравнений
На рисунке 2.1 указана матрица A, вектор x и вектор b. Матрицей А называется основная матрица системы, вектором x – столбец неизвестных, вектором – столбец свободных членов.
Рисунок 2.1 — Матрица A
Согласно свойству элементарных преобразований над строками, основную матрицу этой системы можно привести к треугольному (или ступенчатому) виду (эти же преобразования нужно применять к столбцу свободных членов), что показано на рисунке 2.2
Рисунок 2.2 — Матрица треугольного вида
При этом будем считать, что базисный минор (ненулевой минор максимального порядка) основной матрицы находится в верхнем левом углу, то есть в него входят только коэффициенты при переменных xj1, … , xjr.
Тогда переменные xj1, … , xjr называются главными переменными. Все остальные называются свободными.
Если хотя бы одно число βi ≠ 0, где i > r, то рассматриваемая система несовместна, то есть у неё нет ни одного решения.
Пусть βi ≠ 0 для любых i > r. Перенесём свободные переменные за знаки равенств и поделим каждое из уравнений системы на свой коэффициент при самом левом x (см. рисунок 2.3):
Рисунок 2.3- Несовместная система
Если свободным переменным системы (рисунок 2.3) придавать все возможные значения и решать новую систему относительно главных неизвестных снизу вверх (то есть от нижнего уравнения к верхнему), то мы получим все решения этой системы линейных алгебраических уравнений. Так как эта система получена путём элементарных преобразований над исходной системой, то по теореме об эквивалентности при элементарных преобразованиях системы (рисунок 2) и (рисунок 2.3) эквивалентны, то есть множества их решений совпадают.
2.2 Метод Крамера
Метода Крамера – способ решения систем линейных алгебраических уравнений с числом уравнений равным числу неизвестных с ненулевым главным определителем матрицы коэффициентов системы, причём для таких уравнений решение существует и единственно. Назван по имени Габриэля Крамера, предложившего этот метод в 1750 г.
Рисунок 2.4 — Система линейных уравнений
Для системы n линейных уравнений (рисунок 2.4) с n неизвестными с определителем матрицы системы ≠ 0, решение записывается по формуле показанном на рисунке 2.5:
Рисунок 2.5 — Нахождение решения
i-ый столбец матрицы системы заменяется столбцом свободных членов.
2.3 Метод обратной матрицы
Метод обратной матрицы – метод решения системы линейных алгебраических уравнений, использующий понятие обратной матрицы.
Обратная матрица – такая матрица A −1 , при умножении на которую, исходная матрица A даёт в результате единичную матрицу E (формула 2.6).
Обратная матрица находится по формуле 2.7.
В формуле 2.7 det обозначает определитель.
Если необходимо решить систему линейных уравнений Ax = b, где b – ненулевой вектор, в который входят свободные члены, x – искомый вектор. Если обратная матрица A -1 существует, то x = A -1 b. В противном случае либо размерность пространства решений больше нуля, либо их нет вовсе.
3 ПРОграммная реализация решения задачи
3.1 Введение и общие сведения
Одна из основных задач линейной алгебры – решение систем линейных алгебраических уравнений. Эта задача имеет важное прикладное значение при решении научных и технических проблем. Кроме того, является вспомогательной при реализации многих алгоритмов вычислительной математики, математической физики, обработки результатов экспериментальных исследований.
Программа «MATrix» предназначена для решения систем линейных алгебраических уравнений тремя методами:
- методом Гаусса;
- методом Крамера;
- методом обратной матрицы.
Данный программный продукт значительно упрощает получение корней систем линейных уравнений.
3.2 Структура программного продукта
В процессе разработки программного продукта были реализованы следующие формы:
- Formcs – форма приветсвия;
- MATrix.cs – форма, обеспечивающая решение систем линейных алгебраических уравнений методом Гаусса, методом Крамера или методом обратной матрицы по выбору пользователя;
- About.cs – форма, содержащая информацию о программном продукте.
На рисунке 3.1 изображена функциональная схема.
Видео:ЛИНЕЙНЫЕ УРАВНЕНИЯ - Как решать линейные уравнения // Подготовка к ЕГЭ по МатематикеСкачать

Программирование решения уравнений
Программирование решения уравнений. Презентация, проект и программный продукт (программа в Pascal)
Видео:Python для самых маленьких. Линейные уравнения. Решение задачСкачать

Скачать:
| Вложение | Размер |
|---|---|
| programmirovanie_lineynyh_uravneniy.pptx | 1.54 МБ |
| metod_nyutona.docx | 69.43 КБ |
| programmirovanie_resheniya_uravneniy.docx | 911.13 КБ |
Предварительный просмотр:
Видео:Решение системы линейных алгебраических уравнений (СЛАУ) в Excel МАТРИЧНЫМ МЕТОДОМСкачать

Подписи к слайдам:
Программирование линейных уравнений Работа ученика 9б класса Ф.И.О. обучающегося: Смолькова Андрея Владимировича Руководитель проекта Ф.И.О. Борисова О.А.
Языки программирования — это формальные языки, предназначенные для записи алгоритмов, исполнителем которых будет компьютер. Записи алгоритмов на языках программирования называются программами . Язык Паскаль – универсальный язык программирования. Никлаус Вирт ( 1934 года рождения) — швейцарский учёный, специалист в области информатики, один из известнейших теоретиков в области разработки языков программирования, профессор информатики (компьютерных наук). Разработчик языка Паскаль и ряда других языков программирования.
Метод Гаусса — классический метод решения системы линейных алгебраических уравнений. Это метод последовательного исключения переменных, когда с помощью элементарных преобразований система уравнений приводится к равносильной системе треугольного вида, из которой последовательно, начиная с последних (по номеру), находятся все переменные системы. Метод Гаусса
Метод Ньютона , алгоритм Ньютона (также известный как метод касательных ) — это итерационный численный метод нахождения корня заданной функции. Дана непрерывная функция f ( x ), которая содержит единственный корень на отрезке [ a,b ], где b > a при чем определены непрерывны и сохраняют знак f `( x ) f «( x ). Точность е. Выбираем грубое приближение корня х 0 . Найдем значение функции точке х 0 и проведем касательную до пересечения с осью абсцисс, получим значение х 1 . Определим значение функции в точке х 1 , через эту точку проводим касательную и получаем точку х 2 . Повторим этот процесс n раз. Метод Ньютона
Практически перед каждым программистом рано или поздно встает задача определения корней уравнения. На сегодняшний день существует достаточно много алгоритмов решения данной задачи. Все они могут быть разделены на два этапа: отделения и уточнения корней. Первую часть легко выполнить графическим методом. Для выполнения второго этапа решения уравнения можно воспользоваться одним из многих методов уточнения корней уравнения. Заключение
Видео:Линейное уравнение с одной переменной. 6 класс.Скачать

Предварительный просмотр:
Видео:Решение системы уравнений методом ГауссаСкачать

Предварительный просмотр:
Муниципальное бюджетное общеобразовательное учреждение
«Гимназия №7» г. Торжка
Программирование решения уравнений
Работа ученика 9Б класса
Смольков Андрей Владимирович
Ф.И.О. Борисова Ольга Александровна
Работа допущена к защите «_____» _______________ 2018г.
Подпись руководителя проекта _________________(__________________)
Видео:Видеоурок. 7 класс. Решение линейных уравнений с одним неизвестнымСкачать

Паспорт проекта
Название проекта
Программирование решения уравнений
Руководитель проекта
Борисова Ольга Александровна
Автор проекта
Смольков Андрей Владимирович
Учебная дисциплина
Информатика
Тип проекта
Исследовательский
Цель работы
Изучить программную среду PascalABC для решения уравнений
- Написать программу решения:
- Системы линейных алгебраических уравнений методом Гаусса
- Нелинейных алгебраических уравнений методом Ньютона
Результат проекта (продукт)
Программа в среде программирования PascalABC
Видео:Сколько решений имеет лог. уравнение (!(A *B) + C) IMP (!A * !B + D) = 1. Информатика, ЕГЭ, логикаСкачать

Индивидуальный план работы над проектом
Выбор руководителя и темы проекта.
Выбор типа проекта. Составление плана работы над проектом.
Работа над проектом
Анализ теоретической части.
Составление плана защиты проекта.
Отзыв руководителя. Формирование папки индивидуального проекта.
Защита индивидуального итогового проекта
Видео:Неоднородная система линейных уравненийСкачать

Отзыв
на исследовательскую работу
учащегося 9 б класса МБОУ «Гимназия №7» г. Торжка
Смольков Андрей Владимирович
по теме: «Программирование решения уравнений»
Работа Смолькова Андрея представляет собой исследование программирование решения уравнений. Актуальность работы заключается в том, что на данный момент учащиеся 9-х классов изучают язык программирования Паскаль, и возникла необходимость объединить математику и информатику в единый программный продукт. В работе важно разобраться с различными методами решения уравнений и написать программу. Содержание работы соответствует заявленной теме. Работа включает в себя основную часть, заключение, список литературы. Работу Андрей выполнял самостоятельно, используя материалы Интернета и литературы. При выполнения работы Андрей проявил: самостоятельность, способность решать соответствующие проблемы. Не выполнял все рекомендации научного руководителя и не вовремя устранял замечания. Замечания по данной работе значительные, необходимо продумать и доработать заключение по данной теме. Не достаточно теоретического материала по языку программирования и их разновидности.
Вывод: проектная работа Смолькова А.В. по теме: «Программирование решения уравнений» достигла поставленных целей, отвечает требованиям, предъявляемым к индивидуальному итоговому проекту и рекомендуется к защите.
Учитель информатики . Борисова О.А.
(предмет) (подпись) (расшифровка подписи)
«__»_____________ 2018 г.
Видео:Математика это не ИсламСкачать

Общие сведения о языке программирования Паскаль
Языки программирования — это формальные языки, предназначенные для записи алгоритмов, исполнителем которых будет компьютер. Записи алгоритмов на языках программирования называются программами. Существует несколько тысяч языков программирования. Для данного проекта выбран язык программирования Паскаль, который был разработан в 70-х годах прошлого века Никлаусом Виртом (Швейцария). свое название этот язык получил в честь французского ученого Блеза Паскаля, известного не только своими достижениями в математике, физике и философии, но и созданием первой в мире механической машины, выполнявшей сложение двух чисел.
Язык Паскаль считается универсальным языком программирования, так как он может применяться для записи алгоритмов решения самых разных задач ( вычислительных, обработки текстов, построения графических изображений, поиска информации и т.д.). Он поддерживает процедурный стиль программирования, в соответствии с которым программа представляет собой последовательность операторов, задающих те или иные действия.
Основой языка программирования Паскаль, как и любого другого языка, является алфавит — набор допустимых символов, которые можно использовать для записи программы. Это:
- латинские прописные буквы;
- латинские строчные буквы;
- арабские цифры;
- специальные символы (знак подчеркивания, знаки препинания, круглые, квадратные и фигурные скобки, знаки арифметических операций и д.р.)
В языке существует также некоторое количество различных цепочек символов, рассматриваемых как единые смысловые элементы с фиксированным значением. Такие цепочки символов называются служебными словами.
В программе, записанной на языке Паскаль, можно выделить:
- заголовок программы;
- блок описания используемых данных;
- блок описания действий по преобразованию данных (программный блок).
Заголовок программы состоит из служебного слова program и имени программы. После имени программы ставятся точка с запятой. Блок описания данных состоит из раздела описания констант (const), раздела описания переменных (var) и некоторых других разделов. В разделе описания переменных указываются имена используемых в программе переменных и их типы. Имена переменных одного типа перечисляются через запятую, затем после двоеточия указывается их тип; описание каждого типа заканчивается точкой с запятой.
Общий вид программы:
Видео:Система линейных уравнений. Общее решение. Метод ГауссаСкачать

Решение системы алгебраических уравнений методом Гаусса
Метод Гаусса — классический метод решения системы линейных алгебраических уравнений. Назван в честь немецкого математика Карла Фридриха Гаусса. Это метод последовательного исключения переменных, когда с помощью элементарных преобразований система уравнений приводится к равносильной системе треугольного вида, из которой последовательно, начиная с последних (по номеру), находятся все переменные системы.
В переменную n вводится порядок матрицы системы. С помощью вспомогательной процедуры Input вводятся двумерный массив A и одномерный массив b, после чего оба массива и переменная n передаются функции Gauss. В функции Gauss для каждого k-го шага вычислений выполняется поиск максимального элемента в k-м столбце матрицы начиная с k-й строки. Номер строки, содержащей максимальный элемент сохраняется в переменной l. В том случае если максимальный элемент находится не в k-й строке, строки с номерами k и l меняются местами. Если же все эти элементы равны нулю, то происходит прекращение выполнения функции Gauss c результатом false. После выбора строки выполняется преобразование матрицы по методу Гаусса.
Видео:Решение линейных уравнений.Скачать

Решение нелинейных уравнений
Метод Ньютона , алгоритм Ньютона (также известный как метод касательных ) — это итерационный численный метод нахождения корня заданной функции.
Дана непрерывная функция f(x), которая содержит единственный корень на отрезке [a,b], где b>a при чем определены непрерывны и сохраняют знак f`(x) f«(x). Точность е. Выбираем грубое приближение корня х 0 . Найдем значение функции точке х 0 и проведем касательную до пересечения с осью абсцисс, получим значение х 1 . Определим значение функции в точке х 1 , через эту точку проводим касательную и получаем точку х 2 . Повторим этот процесс n раз.
К сожалению, при всех своих достоинствах метод Ньютона не гарантирует сходимости. Отсутствия решения может возникнуть по нескольким причинам. Например, это может произойти из-за того, что касательная будет параллельна оси абсцисс. В этом случаи необходимо предусмотреть выход из цикла при достижении большого количества итераций.
Существуют также и другие методы, например, золотого сечения. Какой из них использовать решать вам, однако следует отметить, что наиболее быстродейственным считается метод Ньютона, затем метод хорд и последним по быстродействию является метод половинного деления. Хотя количество итераций напрямую зависит от введенных начальных данных. При удачном стечении обстоятельств решение каждым из методов может быть найдено даже при единственной итерации.
Видео:8 Метод простой итерации Ручной счет Решение системы линейных уравнений СЛАУСкачать

Заключение
Практически перед каждым программистом рано или поздно встает задача определения корней уравнения. На сегодняшний день существует достаточно много алгоритмов решения данной задачи. Все они могут быть разделены на два этапа: отделения и уточнения корней. Первую часть легко выполнить графическим методом. Для выполнения второго этапа решения уравнения можно воспользоваться одним из многих методов уточнения корней уравнения.
Язык программирования Паскаль является универсальным языком программирования. В нем можно выполнить самые различные решения уравнений. Язык достаточно прост и понятен для начинающих программистов.
Видео:Линейное уравнение с двумя переменными. 7 класс.Скачать

Список литературы
- Босова Л.Л. Информатика: учебник для 8 класса/ Л.Л. босова, А.Ю. Босова.-3-е изд.-М.: БИНОМ. Лаборатория знаний, 2015. — 160с.:ил.
- http://www.cyberforum.ru
- http://tpdn.ru/library/articles/52/13520
- http://pcfu.ru/metod-gaussa-dlya-resheniya-slau
Видео:Метод Гаусса решения систем линейных уравненийСкачать

Текст публичного выступления
Здравствуйте уважаемые члены комиссии. Я Смольков Андрей, ученик 9Б класса МБОУ «Гимназии №7» города Торжка. Разрешите представить свой исследовательский проект по теме «Программирование решения уравнений». Языки программирования — это формальные языки, предназначенные для записи алгоритмов, исполнителем которых будет компьютер. Записи алгоритмов на языках программирования называются программами. Существует несколько тысяч языков программирования. Для данного проекта выбран язык программирования Паскаль, который был разработан в 70-х годах прошлого века Никлаусом Виртом (Швейцария). Свое название этот язык получил в честь французского ученого Блеза Паскаля, известного не только своими достижениями в математике, физике и философии, но и созданием первой в мире механической машины, выполнявшей сложение двух чисел. Язык Паскаль считается универсальным языком программирования, так как он может применяться для записи алгоритмов решения самых разных задач ( вычислительных, обработки текстов, построения графических изображений, поиска информации и т.д.). Он поддерживает процедурный стиль программирования, в соответствии с которым программа представляет собой последовательность операторов, задающих те или иные действия. Основой языка программирования Паскаль, как и любого другого языка, является алфавит — набор допустимых символов, которые можно использовать для записи программы. Это: латинские прописные буквы; латинские строчные буквы; арабские цифры; специальные символы (знак подчеркивания, знаки препинания, круглые, квадратные и фигурные скобки, знаки арифметических операций и д.р.). В языке существует также некоторое количество различных цепочек символов, рассматриваемых как единые смысловые элементы с фиксированным значением. Такие цепочки символов называются служебными словами. В программе, записанной на языке Паскаль, можно выделить: заголовок программы; блок описания используемых данных; блок описания действий по преобразованию данных (программный блок). Заголовок программы состоит из служебного слова program и имени программы. После имени программы ставятся точка с запятой. Блок описания данных состоит из раздела описания констант (const), раздела описания переменных (var) и некоторых других разделов. В разделе описания переменных указываются имена используемых в программе переменных и их типы. Имена переменных одного типа перечисляются через запятую, затем после двоеточия указывается их тип; описание каждого типа заканчивается точкой с запятой. Общий вид программы:
Метод Гаусса — классический метод решения системы линейных алгебраических уравнений. Назван в честь немецкого математика Карла Фридриха Гаусса. Это метод последовательного исключения переменных, когда с помощью элементарных преобразований система уравнений приводится к равносильной системе треугольного вида, из которой последовательно, начиная с последних (по номеру), находятся все переменные системы. На данных слайдах представлен программный продукт реализации решения уравнения методом Гаусса в Паскале. Метод Ньютона , алгоритм Ньютона (также известный как метод касательных ) — это итерационный численный метод нахождения корня заданной функции. Дана непрерывная функция f(x), которая содержит единственный корень на отрезке [a,b], где b>a при чем определены непрерывны и сохраняют знак f`(x) f«(x). Точность е. Выбираем грубое приближение корня х 0 . Найдем значение функции точке х 0 и проведем касательную до пересечения с осью абсцисс, получим значение х 1 . Определим значение функции в точке х 1 , через эту точку проводим касательную и получаем точку х 2 . Повторим этот процесс n раз. Программа на слайде. К сожалению, при всех своих достоинствах метод Ньютона не гарантирует сходимости. Отсутствия решения может возникнуть по нескольким причинам. Например, это может произойти из-за того, что касательная будет параллельна оси абсцисс. В этом случаи необходимо предусмотреть выход из цикла при достижении большого количества итераций. Практически перед каждым программистом рано или поздно встает задача определения корней уравнения. На сегодняшний день существует достаточно много алгоритмов решения данной задачи. Все они могут быть разделены на два этапа: отделения и уточнения корней. Первую часть легко выполнить графическим методом. Для выполнения второго этапа решения уравнения можно воспользоваться одним из многих методов уточнения корней уравнения.
🎬 Видео
Решение системы линейных уравнений с двумя переменными способом подстановки. 6 класс.Скачать

Решение системы линейных уравнений графическим методом. 7 класс.Скачать

Математика. Линейные диофантовы уравнения с двумя неизвестными. Центр онлайн-обучения «Фоксфорд»Скачать