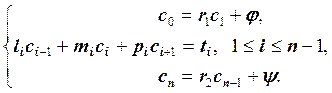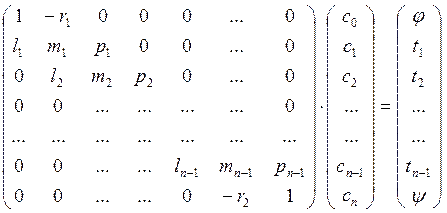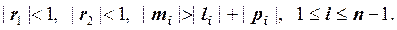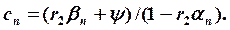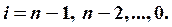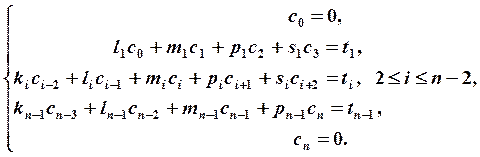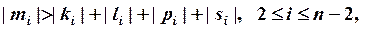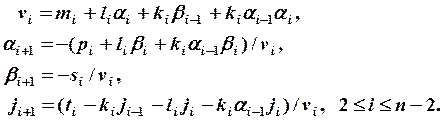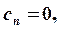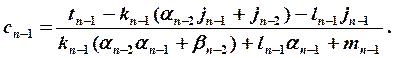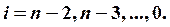Трехдиагональная линейная система уравнений может быть записана в следующем виде:
Решение ищется в виде:
ui-1=beti*ui+gami В этом случае для bet и gam получаются рекуррентные формулы: beti+1=ci*fi, gami+1=(fi+ai*gami)*fi, fi=1/(bi-ai*beti); bet0=gam0=0. По этим формулам вспомогательные массивы вычисляются для i от 1 до N, затем находится uN-1=gamN, а затем при известных вспомогательных массивах вычисляются все значения u.
Алгоритм принципиально не может иметь ведущего элемента, и есть вероятность того, что он не сойдется даже для несингулярной матрицы. Для этого в программе, реализующей прогонку, необходимо контролировать значения fi. Еще два замечания: длины рекуррентных цепочек порядка N, поэтому при экспоненциальном накоплении погрешностей (что происходит при преобладании значений |beti|>1) прогонка практически обязательно разойдется. Второе: алгоритм сохраняет исходные значения коэффициентов. Доказано, что для устойчивой работы алгоритма Томаса достаточно диагонального преобладания, однако, во многих случаях он сходится и при отсутствии такового.
Общее описание алгоритма таково.
Если провести исключение из имеющейся системы уравнений всех уравнений, находящихся на нечетных позициях, то от системы N исходных уравнений мы перейдем к системе из (N-1)/2+1 уравнений только для четных значений u, нечетные же значения будут вычисляться через четные. Повторяя эту процедуру для укороченной системы, мы в конце концов придем к единственному уравнению для узла, лежащего в позиции (N-1)/2 (только если N-1 — степень двойки). Затем, проводя обратную подстановку, определяются крайние, а затем и все прочие узлы.
Формулы для пересчета коэффициентов на каждом этапе исключения таковы:
Если число уравнений не является степенью двойки, алгоритм реализуется методом фиктивного восполнения области определения до степени 2. При этом никаких реальных действий, кроме нескольких целочисленных проверок, не производится, а только коэффициенты, индекс которых выпадает из области определения [0,N-1] включительно, считаются равными нулю и в преобразованиях не участвуют (подробности в программе).
Особая устойчивость этого алгоритма по сравнению с алгоритмом Томаса связана с тем, что длина рекуррентных цепочек здесь не превышает log2(N)+1, и в связи с этим даже при экспоненциальном росте погрешности исходный результат будет ограниченным. Кроме того, в алгоритме Томаса в рекуррентных цепочках производятся операции между коэффициентами соседних узлов, при редукции на этапах больших начального — между далеко отстоящими, что уменьшает вероятность образования погрешности при вычитании двух близких чисел. Проверено, что алгоритм редукции успешно работает во многих случаях, когда алгоритм Томаса (прогонка) расходится.
Алгоритм не требует дополнительной памяти, но сохраняет только половину из имеющихся в начале его работы коэффициентов: те, что находятся на нечетных позициях (независимо от четности N). Скорость работы почти не зависит от того, является ли N-1 целочисленной степенью 2.
Ниже приводятся программы для прогонки и редукции.
Видео:Метод Крамера за 3 минуты. Решение системы линейных уравнений - bezbotvyСкачать

Линейные уравнения. Решение систем линейных уравнений. Метод прогонки.
Метод прогонки (алгоритм Томаса) используют для решения СЛУ типа Ax=F, где A — трёхдиагональная матрица. Это вариант метода последовательного исключения неизвестных.
Система уравнений Ax=F равноценна соотношению:
Метод прогонки базируется на предположении, что неизвестные, которые необходимо найти, связаны соотношением:
Выразим xi-1 и xi через xi+1, подставим в уравнение, используя это соотношение, (1):
где Fi — правая часть i-го уравнения.
Это соотношение выполняется не завися от решения, если потребовать:


Получаем из 1-го уравнения:

После того, как нашли прогоночные коэффициенты α и β, используем уравнение (2) и получим решение системы. Причем,

Еще одним вариантом объяснения смысла метода прогонки является такой вариант: преобразуем уравнение (1) к равнозначному ему уравнению:
c надиагональной (наддиагональной) матрицей:
Рассчеты проводим в 2 этапа. На 1-ом этапе вычисляем компоненты матрицы C′i и вектора F′, начиная с i=2 до i=n:
На 2-ом этапе, для i=n,n−1,…,1 вычисляем решение:
Для применимости формул метода прогонки достаточно свойства строгого диагонального преобладания у матрицы A.
Видео:Система линейных уравнений. Метод обратной матрицы. Матричный метод.Скачать

Метод прогонки для трехдиагональных матриц
Страницы работы
Содержание работы
1. Метод прогонки
Метод прогонки – это метод решения систем линейных уравнений с ленточными матрицами, т.е. матрицами, большая часть элементов которых равна нулю, а ненулевые элементы расположены на нескольких диагоналях. Более строго, матрица, для элементов которой выполняется условие 

Использование метода Гаусса для решения систем линейных уравнений с ленточными матрицами нерационально, так как большая часть времени работы программы будет тратиться на обработку нулевых элементов. Метод прогонки можно рассматривать как частный случай метода Гаусса, в котором учитывается то, что большая часть элементов матрицы равна нулю. Напомним, что для реализации метода Гаусса требуется 
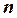
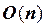
1.1. МЕТОД ПРОГОНКИ ДЛЯ ТРЕХДИАГОНАЛЬНЫХ МАТРИЦ
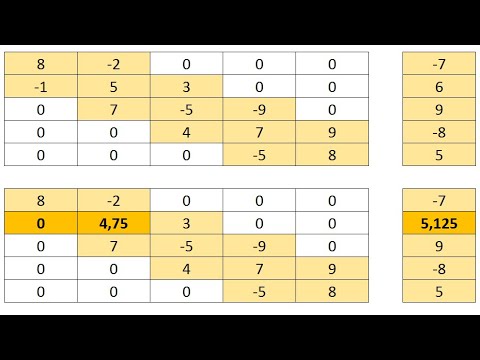
Запишем систему линейных уравнений 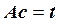
Рассмотрим метод прогонки для матрицы с диагональным преобразованием, то есть для таких квадратных матриц 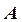

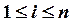
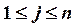
Напомним, что матрица с диагональным преобладанием невырожденна.
Для трехдиагональной матрицы, рассмотренной выше, условия диагонального преобладания записываются следующим образом:
Для матрицы с диагональным преобладанием метод прогонки – это частный случай метода Гаусса, в котором автоматически используется в качестве ведущего элемента максимальный по модулю элемент в строке и учитывается тот факт, что большая часть элементов матрицы равна нулю.
Идея метода прогонки заключается в том, что неизвестное 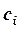
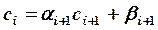
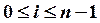
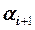
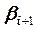
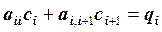
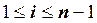

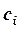
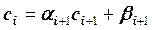
Приведем формулы метода прогонки.
1. На первом этапе находим 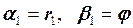
2. Затем, в порядке возрастания индексов, находим остальные прогоночные коэффициенты по формулам:
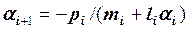
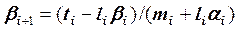
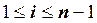
Первые два этапа называют прямой прогонкой. Отметим, что они аналогичны прямому ходу метода Гаусса.
3. Находим неизвестное 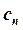
4. Находим неизвестные 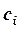
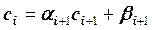
Два последних этапа называют обратной прогонкой.
Рассмотрим устойчивость метода прогонки. Формулы метода прогонки можно применять, если знаменатели дробей при вычислении 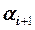
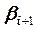
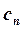
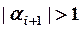
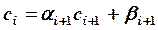
Теорема (корректность и устойчивость метода прогонки). Если выполняются неравенства 
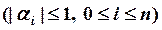
Число арифметических действий, необходимых для реализации метода прогонки, пропорционально числу неизвестных — 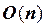
1.2. МЕТОД ПРОГОНКИ ДЛЯ ПЯТИДИАГОНАЛЬНЫХ МАТРИЦ
Рассмотрим метод прогонки для пятидиагональных матриц с диагональным преобладанием. Запишем систему линейных уравнений:
Именно в таком виде записывается система линейных уравнений при нахождении коэффициентов естественного сглаживающего кубического сплайна.
Будем полагать, что выполняются условия диагонального преобладания:
Напомним, что при выполнении этих условий система линейных уравнений имеет единственное решение.
Идея метода прогонки для пятидиагональных матриц заключается в том, что неизвестное 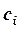
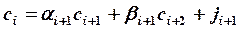
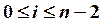
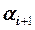
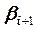
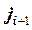
Приведем формулы метода прогонки.
1. На первом этапе находим значения
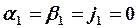
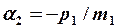

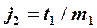
2. Затем, в порядке возрастания индексов, находим остальные прогоночные коэффициенты по формулам:
Первые два этапа называют прямой прогонкой.
3. Находим неизвестные 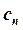
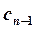
4. Находим неизвестные 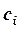
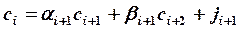
Два последних этапа называют обратной прогонкой.
2. СПЛАЙН – ИНТЕРПОЛЯЦИЯ
Напомним основные определения.
Определение сетки.Рассмотрим отрезок 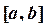
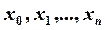
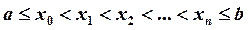
Множество точек 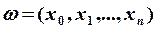
📺 Видео
Математика без Ху!ни. Метод Гаусса.Скачать

Математика без Ху!ни. Метод Гаусса. Совместность системы. Ранг матрицы.Скачать

Лекция 13. Исследование систем линейных уравнений. Теорема Кронекера — Капелли.Скачать

Решение системы уравнений методом обратной матрицы - bezbotvyСкачать

Решение матричных уравненийСкачать

Решение системы уравнений методом ГауссаСкачать

Система с тремя переменнымиСкачать

Метод Гаусса решения систем линейных уравненийСкачать

2.1 Точные методы решения СЛАУ (Крамера, Гаусса, Жордана, прогонки)Скачать
Линейная алгебра, Матрицы: Метод Гаусса. Высшая математикаСкачать

Решение системы уравнений методом Гаусса. Бесконечное множество решенийСкачать

ЛИНЕЙНЫЕ УРАВНЕНИЯ - Как решать линейные уравнения // Подготовка к ЕГЭ по МатематикеСкачать

Лекция 8. Решение матричных уравненийСкачать

Линейная алгебра: матрицы, определители, метод Крамера. Высшая математикаСкачать

Метод Гаусса и метод Жордана-ГауссаСкачать

Урок 1. Матрицы, определитель матрицы и ранг матрицы | Высшая математика | TutorOnlineСкачать

6 5 Формула для обратной матрицы и линейные уравнениЯСкачать