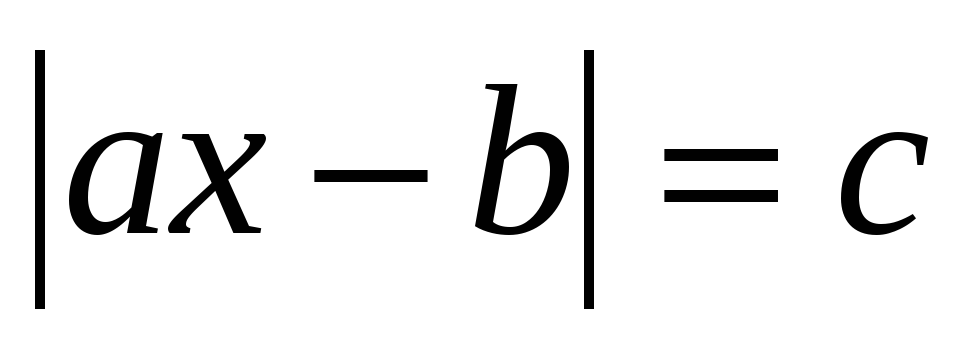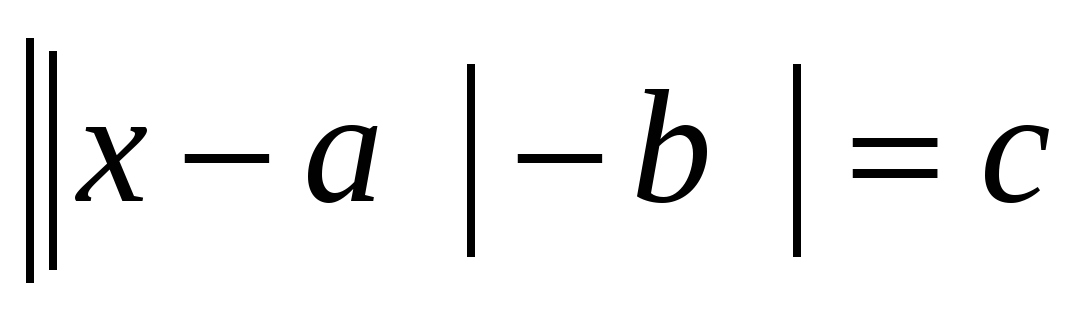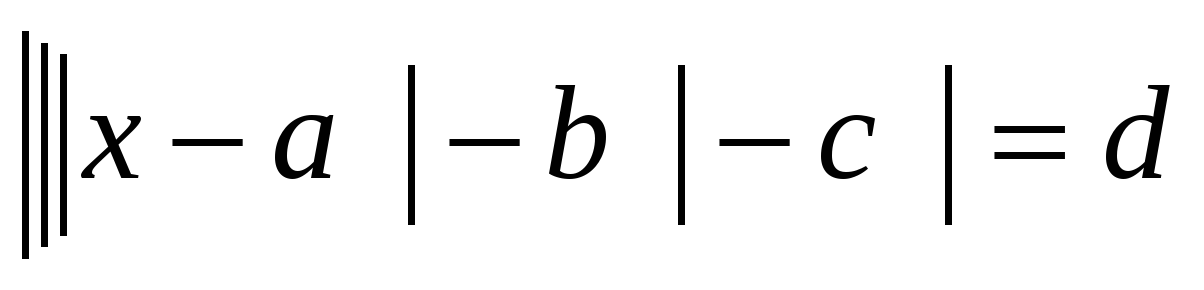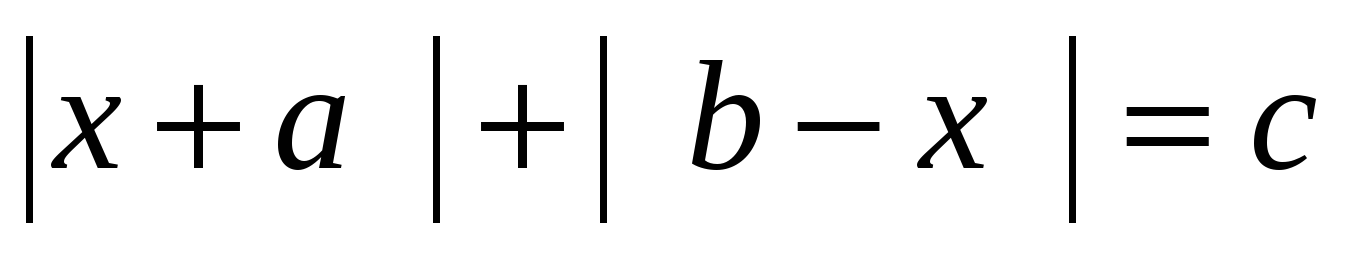Решение линейных уравнений с модулем проект

Видео:Уравнения с модулемСкачать

Исследовательская работа по математике на тему: «Способы решения линейных уравнений, содержащих знак модуля».

Понятие «модуль» широко применяется во многих разделах школьного курса математики, например, в изучении абсолютной и относительной погрешностей приближенного числа; в геометрии и физике будут изучаться понятия вектора и его длины (модуля вектора). Понятия модуля применяется в курсах высшей математики, физики и технических наук, изучаемых в высших учебных заведениях. Несмотря на то, что тема «Модуль числа» проходит «красной нитью» через весь курс школьной и высшей математики, для ее изучения по программе отводится очень мало времени (в 6 классе -2 часа, в 8 классе — 4 часа).

Исходя из всего вышесказанного, возникает проблема: найти разнообразные методы в обучении решению задач с модулем.

Практически у каждого обучающегося вызывают затруднения задания, содержащие модуль. Это один из самых трудных материалов, с которыми школьники сталкиваются на экзаменах (в заданиях ЕГЭ это задания С5 и С6).

Считаю, что эта тема требует более глубокого исследования, так как она прослеживается в различных заданиях повышенной сложности, которые предлагают учащимся авторы дидактических материалов, в задачах математических олимпиад, в заданиях вступительных экзаменов в Высшие Учебные Заведения и на ЕГЭ.

Указанные обстоятельства обусловили мой выбор темы исследовательской работы.

Основной целью работы считаю получение расширенной информации о модуле числа, его применении, а также о различных способах решения уравнений, содержащих знак абсолютной величины.

Цель исследовательской работы определяет следующие задачи:

— показать необходимость более глубокого рассмотрения темы «Решение линейных уравнений, содержащих знак модуля» в школьной программе;

— разработать алгебраический метод решения линейных уравнений, содержащих знак модуля;

— разработать графический методы решения линейных уравнений, содержащих знак модуля.

Я предположила, что в результате исследования я смогу показать своим одноклассникам и друзьям, что решение уравнений с модулями не являются одним из сложнейших заданий.

Формулирование цели исследовательской работы определяет:

объект исследования – решение уравнений, содержащих знак абсолютной величины;

предмет исследования – алгебраический и графический методы решения линейных уравнений, содержащих знак модуля.

Видео:Уравнения с модулем. Что такое модуль числа. Алгебра 7 класс.Скачать

Проект «Решение уравнений с модулем»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

«Актуальность создания школьных служб примирения/медиации в образовательных организациях»

Свидетельство и скидка на обучение каждому участнику

Выберите документ из архива для просмотра:

Выбранный для просмотра документ Математика.pptx

Описание презентации по отдельным слайдам:

Математика. 10- 11 классы

Решение уравнений, содержащих знак модуля

Цель проекта изучение способов решения уравнений , содержащих модуль.

Ход проекта I ОПРЕДЕЛЕНИЕ МОДУЛЯ

ОПРЕДЕЛЕНИЕ МОДУЛЯ | a | =

Алгоритм решения уравнений по определению

Пример 1 |x³ +x+1| = |x³ +3x-1|

Данное уравнение равносильно совокупности двух уравнений : 1 СПОСОБ РЕШЕНИЕ УРАВНЕНИЙ С МОДУЛЕМ ПО ОПРЕДЕЛЕНИЮ 1. x³ +x+1=x³ +3x-1 и 2. x³ +x+1=-(x³ +3x-1) Решаем эти уравнения и получаем корни х1 =1, x2 =0 3.Проверка корней. Ответ: 0;1

2 способ Алгоритм решения уравнений способом возведения в квадрат обеих частей уравнения Возведем в квадрат обе части уравнения Решим полученное уравнение Сделаем проверку Запишем ответ

Пример 2 Решить уравнение: | 2x-1|=|x+3|

Решение: возводим левую и правую части данного уравнения в квадрат, получаем равносильное уравнение (2x-1)² =(x+3)², корнями которого, а значит и исходного уравнения, являются числа х =- 2/3 и х = 4 Ответ:

3 СПОСОБ решение уравнений с модулем с использованием числовой оси

Решаем совокупность систем

Выбранный для просмотра документ ПРОЕКТ Решение уравнений с модулем.docx

«Решение уравнений с модулем»

Тема проекта «Решение уравнений с модулем»

Участники проекта: обучающиеся 11 класса Тюхтин Евгений и Яковлева Светлана

Руководитель проекта: учитель математики Олейникова Г.М.

Краткая аннотация проекта

Вопросы, направляющие проект

Пример продукта проектной деятельности

Критерии оценки проекта

10.Материалы по сопровождению и поддержке проектной деятельности.

Краткая аннотация проекта

Проект может быть использован при изучении темы «Решение уравнений с модулем» в 10-11 классах. Применяться при подготовке к единому государственному экзамену.

Данная работа позволяет увидеть различные способы решения уравнений с модулем: по определению, возведение в квадрат, с помощью числовой прямой.

Данный проект позволит обучающимся расширить объем знаний по данной теме, развивать специальные и общеучебные умения .

Развивать коммуникативные способности обучающихся, навыки исследовательской работы.

Учить обобщать и систематизировать, применять на практике .

Что участие в проекте даст его участникам

После завершения проекта обучающиеся смогут

— знать определение модуля, решать уравнения с модулем по определению;

— решать уравнения с модулем способом возведения в квадрат обеих частей уравнения;

— уметь решать уравнения с модулем, использую числовую ось, определяя знак модуля на промежутках;

— уметь раскрывать знак модуля;

— научаться работать по алгоритму;

— приобретут навыки, умения ориентироваться в информационной среде.

Оформление материалов исследования.

Обсуждение темы проекта

Последовательность подачи материала

Обсуждение форм представления работы

Подведение итогов, оценивание.

Вопросы, направляющие проект

Способы решения уравнений с модулем?

Можно ли решить уравнение с модулем используя определение модуля?

Можно ли решить уравнение с модулем используя другие способы решения?

Можно ли составить алгоритмы решения уравнения с модулем?

«Решение уравнений с модулем по определению модуля»

«Решение уравнений с модулем способом возведения в квадрат»

«Решение уравнений с модулем с использованием числовой оси»

Карточки с заданиями

Критерии оценки проекта

Самостоятельность работы над проектом

Актуальность и значимость темы

Полнота раскрытия темы

Оригинальность решения проблемы

Презентация содержания проекта

Использование средств наглядности, технические средства

Ответы и вопросы

Материалы по сопровождению и поддержке проектной деятельности:

С.М. Никольский «Алгебра и начала математического анализа» изд. Просвещение 2009 г

Р.Б. Райхмист «Задачник по математике» изд. «Московский лицей» Москва 2003 г.

Е.Е. Калугина «Уравнения, содержащие знак модуля» изд. «Илекса» Москва 2010 г.

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 949 человек из 80 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 681 человек из 75 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 314 человек из 70 регионов

Ищем педагогов в команду «Инфоурок»

Видео:Как решать уравнения с модулем или Математический торт с кремом (часть 1) | МатематикаСкачать

Дистанционные курсы для педагогов

Самые массовые международные дистанционные

Школьные Инфоконкурсы 2022

33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 566 123 материала в базе

Другие материалы

• 22.10.2016
• 328
• 0

• 22.10.2016
• 10270
• 130

• 22.10.2016
• 381
• 0

• 22.10.2016
• 333
• 0

• 22.10.2016
• 1057
• 5

• 22.10.2016
• 740
• 2

• 22.10.2016
• 329
• 1

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

• 22.10.2016 2394
• RAR 442.4 кбайт
• 27 скачиваний
• Рейтинг: 4 из 5
• Оцените материал:

Настоящий материал опубликован пользователем Олейникова Галина Михайловна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

• На сайте: 5 лет и 3 месяца
• Подписчики: 0
• Всего просмотров: 23186
• Всего материалов: 10

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Видео:Линейные уравнения с одной переменной, содержащие переменную под знаком модуля. 6 класс.Скачать

Дистанционные курсы
для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

У 76% российских учителей оклад ниже МРОТ

Время чтения: 2 минуты

ЕГЭ в 2022 году будут сдавать почти 737 тыс. человек

Время чтения: 2 минуты

Объявлен конкурс дизайн-проектов для школьных пространств

Время чтения: 2 минуты

Тринадцатилетняя школьница из Индии разработала приложение против буллинга

Время чтения: 1 минута

Профессия педагога на третьем месте по популярности среди абитуриентов

Время чтения: 1 минута

В Рособрнадзоре рассказали, как будет меняться ЕГЭ

Время чтения: 2 минуты

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Видео:Модуль числа. Практическая часть. 6 класс.Скачать

Решение линейных уравнений с модулями

В данной работе рассмотрены различные способы решения уравнений с модулями.

Просмотр содержимого документа
«Введение»

Решение уравнений с модулем – это сложная и важная тема в курсе алгебры. Уравнения с модулем относятся к разделу заданий повышенной сложности и на экзаменах за их решение ставятся высокие баллы. Поэтому мы решили создать проект, который поможет ребятам научиться решать уравнения с модулем. Данный проект разрабатывался учащимися седьмых классов, и в нем рассматривается решение линейных уравнений с модулем.

Поскольку уравнения с модулем не входят в обязательный курс алгебры, то эта тема изучается на элективных курсах. Целью этого проекта было: создать методический и дидактический материал с использованием компьютерных технологий для проведения элективного курса по теме: «Решение линейных уравнений с модулем в 7 классе».

Перед учащимися стояла задачи:

1) за время работы над проектом научиться решать линейные уравнения с модулем различного уровня сложности несколькими методами;
2) для уравнений различного уровня сложности вида:

применить следующие методы решения:

решение линейных уравнений с модулем методом интервалов;

решение линейных уравнений с модулем с использованием геометрического смысла;

решение линейных уравнений с модулем графическим способом;

решение линейных уравнений с модулем с использованием компьютерных технологий — электронных таблиц Excel ;

и для каждого вида уравнений подготовить методические пособия:

карточки — образцы решения этого уравнения каждым из перечисленных способов;

презентации с подробным алгоритмом решения этого уравнения;

карточки – задания для решения уравнений на уроках и на контрольных работах
( 4 варианта по 6 заданий)

ответы к карточкам – заданиям.

Эти пособия планируется использовать во время изучения данной темы на элективном курсе.

Работая над проектом, учащиеся седьмых классов освоили различные методы решения линейных уравнений с модулями, создали карточки-задания и карточки — образцы, которые можно применять для работы на уроках, для проведения самостоятельных и контрольных работ.
Дидактических материалов такого вида не было !
Все уравнения, а их всего 150, учащиеся прорешали, чтобы получить для них ответы. Кроме того, были созданы красочные презентации, которые дают наглядность при изучении данной темы, и прибор, позволяющий решать уравнения с использованием геометрического смысла модуля.

Этот проект является первым этапом в решении такой сложной темы, как « Решение уравнений с модулем».
Мы планируем продолжить эту работу, рассмотрев решение квадратных уравнений с модулями на элективных курсах.

Просмотр содержимого презентации
«ПроектЛинейные уравнения с модулями»

Создать методический и дидактический материал с использованием компьютерных технологий для проведения элективного курса по теме: «Решение линейных уравнений с модулем» в 7 классе.

Это многозначное слово, которое имеет множество значений и применяется не только в математике , но и в архитектуре, физике, технике, программировании и других точных науках .

это исходная единица измерения, устанавливаемая для данного архитектурного сооружения.

термин модуль не имеет универсального значения. Служит для обозначения различных коэффициентов и величин ( модуль зацепления, модуль упругости, модуль сравнения, модуль захвата, модуль сжатия и др.).

при разработке больших проектов программу разбивают на отдельные модули –

относительно независимые и самостоятельные программы. Это упрощает написание, отладку и внедрение проекта.

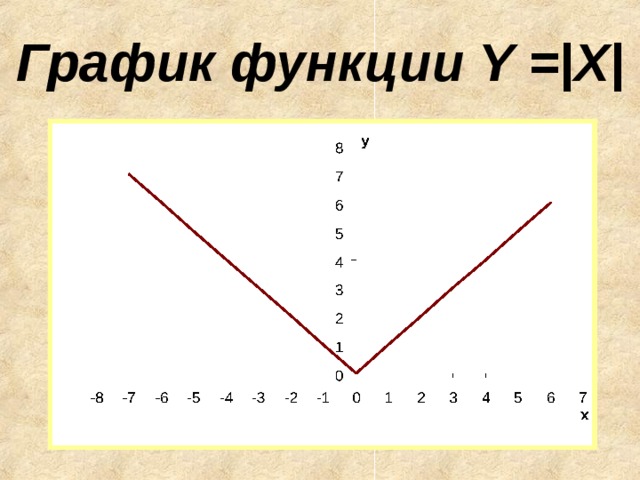
величина́ или мо́дуль , обозначается |x|. В случае вещественного аргумента — это непрерывная

кусочно-линейная функция, определённая таким образом:

если Х

С геометрической точки зрения, модуль числа есть расстояние между числом и точкой отсчета. В математике широко используется тот факт, что геометрически величина |x 1 — x 2 | означает расстояние между точками x 1 и x 2 и, таким образом, может быть использована как мера близости одной величины к другой.

На элективных курсах рассматривались уравнения разного уровня сложности:

Для решения линейных уравнений с модулем рассматривались различные методы:

• метод интервалов;

• графический метод;

• использование геометрического смысла модуля;

• применение компьютерных технологий – электронных таблиц Excel.

Тема: «Решение линейных уравнений с модулем».

1)|x — 2| + |3 + x| = 2x + 1

|x — 2| + |3 + x| = 2x + 1

Для каждого вида уравнений были подготовлены:

 карточки — образцы решения этого уравнения каждым из перечисленных способов;

• презентации с подробным алгоритмом решения этого уравнения;
• карточки – задания для решения уравнений на уроках и на контрольных работах ( 4 варианта по 6 заданий);
• ответы к карточкам – заданиям.

был изготовлен прибор, позволяющий, решать линейные уравнения с модулем используя геометрический смысл.

Сейчас мы покажем вам решение уравнения вида: различными способами.

Презентация, показывающая решение уравнения методом интервалов с построением графика.

=3 ; ||x-3-3|-3|=||x-6|-3| |||x-3|-3|-3|=||-x-3-3|-3|, если x||-x|-3| ||x-6|-3| x 3″ width=»640″

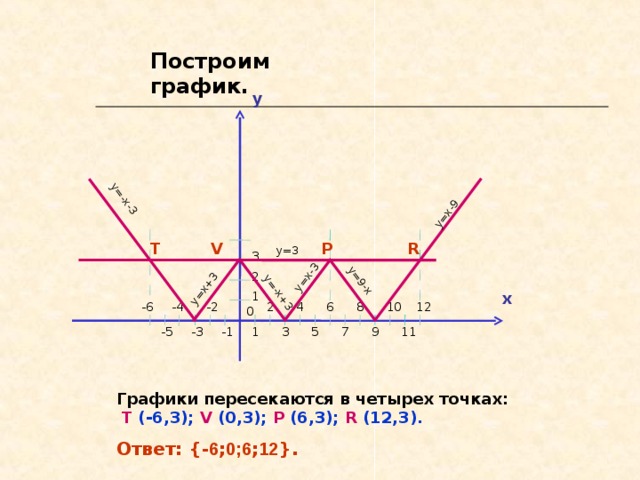
Решение уравнения с модулями вида: |||x-3|-3|-3|=3.

Строим графики функций y=|||x-3|-3|-3|; y=3 в одной системе координат.

1) Преобразуем выражение |||x-3|-3|-3|, применив метод интервалов

=9; y=9-x, если 6 . 2) При x Преобразуем выражение ||x|-3|, применив метод интервалов. x=0. 1 . Преобразуем выражение |x-3|, применив метод интервалов. |x-3| |-x-3| x 0 3 |x-3| x 0 3″ width=»640″

Преобразуем выражение ||x|-3|, применив метод интервалов.

Преобразуем выражение |x-3|, применив метод интервалов.

Преобразуем выражение |-x-3|, применив метод интервалов.

=9.» width=»640″

Получаем функцию, заданную несколькими формулами. Заметим, что каждая формула представляет собой линейную функцию, графиком которой является прямая. Для построения будем использовать таблицы.

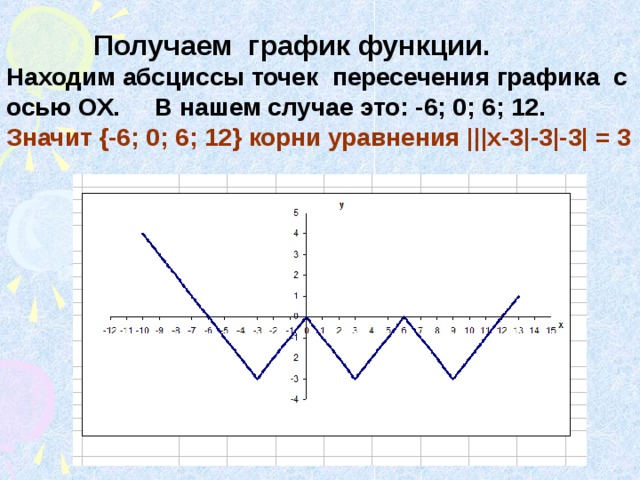
Графики пересекаются в четырех точках: T (-6,3); V (0,3); P (6,3); R (12,3).

Карточка – образец, показывающая решение уравнения с использованием геометрического смысла модуля.

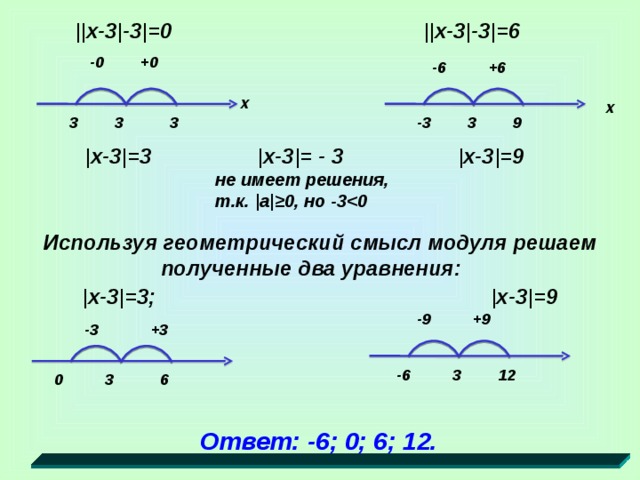
Решение уравнения вида |||x-3|-3|-3|=3 используя геометрический смысл модуля.

Пусть ||x-3|-3| = а, то уравнение принимает вид: | а -3| = 3

Используя геометрический смысл модуля получаем:

Вернемся к прежней переменной и получим два уравнения:

Используя геометрический смысл модуля решаем эти уравнения.

|x-3| = — 3 не имеет решения, т.к. | а |≥ 0, но -3

Используя геометрический смысл модуля решаем полученные два уравнения: |x-3| =3; |x-3| =9

Презентация, показывающая графическое решение уравнений с модулем с использованием компьютерных технологий – Excel

Решим линейное уравнение с модулями при помощи Excel

• Составляем таблицу значений Х и У для построения графика.
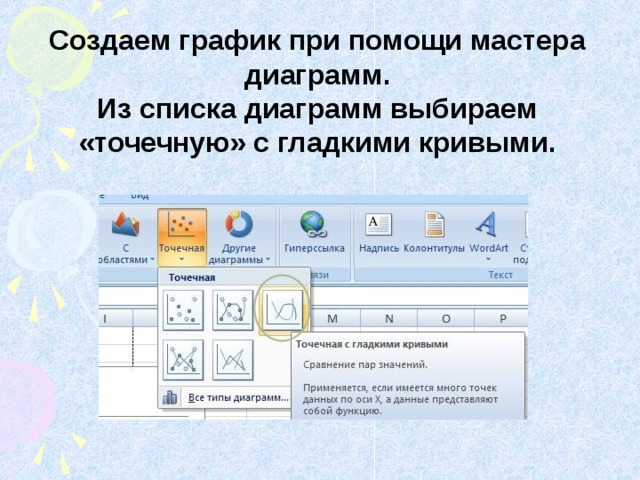
• Выделяем таблицу и открываем мастер диаграмм.
• Выбираем в мастере диаграмм «точечную» диаграмму.
• Создаем диаграмму с заголовком, подписями осей.
• Находим значения корней уравнения – это абсциссы точек пересечения графика с осью ОХ.

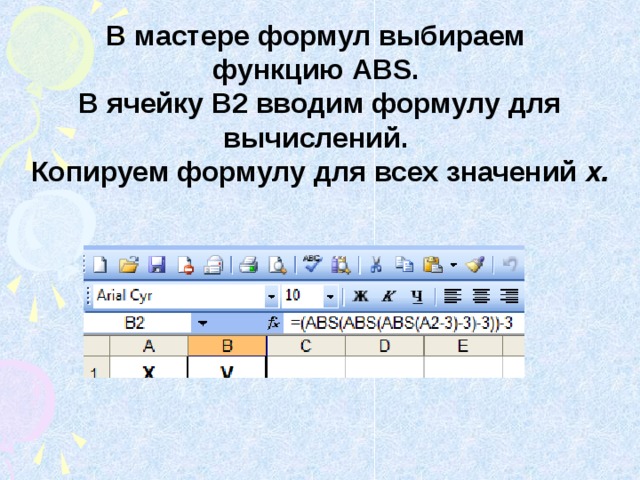
Составим столбец значений Х для получения графика, используя автозаполнение. Возьмем х  [- 10 ; 13 ]

Напишем числа: -10; -9,5 .

Выделим ячейки с этими числами и протянем за маркер заполнения вниз, пока не получим число 10. Будет вот такой столбик c заголовком Х .

В мастере формул выбираем функцию ABS . В ячейку В2 вводим формулу для вычислений. Копируем формулу для всех значений х.

Создаем график при помощи мастера диаграмм.

Из списка диаграмм выбираем «точечную» с гладкими кривыми.

Получаем график функции. Находим абсциссы точек пересечения графика с осью ОХ. В нашем случае это: -6; 0; 6; 12.

Значит корни уравнения |||x-3|-3|-3| = 3

Карточки – задания для решения уравнений на уроках и на контрольных работах ( 4 варианта по 6 заданий).

Решение уравнений типа

Решение уравнений типа

• |||7-3x|-8|+4|=28
• |||5-8x|-3|+2|=32
• |||4-3x|+2|-10|=28
• |||15x-10|-23|+5|=35
• |||10-x|-3|+9|=18
• |||7x+6|+8|-10|= 16

Ответы для уравнений с модулем:

В следующем году мы продолжим эту работу, рассмотрев решение квадратных уравнений с модулями на уроках математики и информатики. В перспективе это уравнения вида: ax 2 + b|x| + c = 0; | ax 2 + bx + c |= 0; |ax 2 + b|x| + c|= 0; |a|x 2 | + b|x|+c|=0.

Список используемой литературы.

• Васюк Н.В., Мартиросян М.А., Слепенкова Е.В., Уединов А.Б., Чулков П.В. «Алгебра 7класс. Дидактические материалы», ИП Милосердов И.В. ,2010 год.
• Ершова А.И., Голобородько В.В., Ершова А.С. «Самостоятельные и контрольные работы по алгебре и геометрии для 7 класса», Москва, ИЛЕКСА, 2010 год.
• Кострикина Н.П. «Задачи повышенной трудности в курсе алгебры 7-9 классов», Москва, Просвещение, 1991 год.
• Вавилов В.В., Мельников И.И., Олехник С.Н., Пасиченко Н.И. «Задачи по математике. Алгебра», Москва, Наука, 1987 год.
• Вавилов В.В., Мельников И.И., Олехник С.Н., Пасиченко Н.И. «Задачи по математике. Уравнения и неравенства», Москва, Наука, 1987 год.
• Родионов Е.М. «Справочник по математике для поступающих в ВУЗЫ», МЦ «Аспект», 1992 год.
• Говоров В.М., Дыбов П.Т., Мирошин Н.В., Смирнова С.Ф. «Сборник конкурсных задач по математике», Москва, Наука, 1986 год.
• Кузнецова Л.В., Суворова С.Б., Бунимович Е.А., Колесникова Т.В., Рослова Л.О. «Алгебра. Сборник заданий для подготовки к ГИА в 9 классе», Москва, Просвещение, 2010 год.
• Интернет.

учитель математики — Скородумова Татьяна Васильевна

учитель информатики -Захарова Антонина Николаевна.

📹 Видео

Как решать уравнение с модулем Уравнение с модулями как решать Как раскрыть модуль в уравненииСкачать

Решение линейных уравнений с модулями.Скачать

Контрольная работа. Уравнения с МОДУЛЕМСкачать

Уравнения с модулем. Часть 2 | Математика | TutorOnlineСкачать

Сложное уравнения с модулем. Алгебра 7 класс.Скачать

Неравенства с модулем | Математика | TutorOnlineСкачать

Модуль в модуле в уравнении. Алгебра 7 класс.Скачать

УРАВНЕНИЯ С МОДУЛЕМ | метод интерваловСкачать

Решение простого уравнения с модулем. #ShortsСкачать

Решение линейных неравенств с одной переменной, содержащих переменную под знаком модуля. 6 класс.Скачать

Решение уравнения с модулем |x+8|+|x-3|+|x+2|=1.Скачать

Уравнение с модулем. 7 класс. Модуль. часть 4Скачать

Линейные уравнения с одной переменной, содержащие переменную под знаком модуля. Практ. ч. 6 класс.Скачать

6 класс. Решение уравнений с модулями.Скачать

УРАВНЕНИЯ С МОДУЛЕМ. Метод интервалов для решения уравнений.Скачать