Решение линейных уравнений python sympy

Что такое SymPy ? Это библиотека символьной математики языка Python. Она является реальной альтернативой таким математическим пакетам как Mathematica или Maple и обладает очень простым и легко расширяемым кодом. SymPy написана исключительно на языке Python и не требует никаких сторонних библиотек.

Документацию и исходный код этой библиотеки можно найти на ее официальной странице.

Видео:Использование библиотеки SymPy для работы с системами уравнений в PythonСкачать

Первые шаги с SymPy

Используем SymPy как обычный калькулятор

В библиотеке SymPy есть три встроенных численных типа данных: Real , Rational и Integer . С Real и Integer все понятно, а класс Rational представляет рациональное число как пару чисел: числитель и знаменатель рациональной дроби. Таким образом, Rational(1, 2) представляет собой 1/2 , а, например, Rational(5, 2) — соответственно 5/2 .

Библиотека SymPy использует библиотеку mpmath , что позволяет производить вычисления с произвольной точностью. Таким образом, ряд констант (например, пи, e), которые в данной библиотеке рассматриваются как символы, могут быть вычислены с любой точностью.

Как можно заметить, функция evalf() дает на выходе число с плавающей точкой.

В SymPy есть также класс, представляющий такое понятие в математике, как бесконечность. Он обозначается следующим образом: oo .

Символы

В отличие от ряда других систем компьютерной алгебры, в SymPy можно в явном виде задавать символьные переменные. Это происходит следующим образом:

После их задания, с ними можно производить различные манипуляции.

С символами можно производить преобразования с использованием некоторых операторов языка Python. А именно, арифметических ( + , -` , «* , ** ) и логических ( & , | ,

Библиотека SymPy позволяет задавать форму вывода результатов на экран. Обычно мы используем формат такого вида:

Видео:Библиотека SymPy для алгебраических операций в PythonСкачать

Алгебраические преобразования

SymPy способна на сложные алгебраические преобразования. Здесь мы рассмотрим наиболее востребованные из них, а именно раскрытие скобок и упрощение выражений.

Раскрытие скобок

Чтобы раскрыть скобки в алгебраических выражениях, используйте следующий синтаксис:

При помощи ключевого слова можно добавить поддержку работы с комплексными переменными, а также раскрытие скобок в тригонометрических функциях.

Упрощение выражений

Если вы хотите привести выражение к более простому виду (возможно, сократить какие-то члены), то используйте функцию simplify .

Также надо сказать, что для определенных видов математических функций существуют альтернативные, более конкретные функции для упрощения выражений. Так, для упрощения степенных функций есть функция powsimp , для тригонометрических — trigsimp , а для логарифмических — logcombine , radsimp .

Видео:Решения системы линейных уравнений на Python (Sympy).Скачать

Вычисления

Вычисления пределов

Для вычисления пределов в SymPy предусмотрен очень простой синтаксис, а именно limit(function, variable, point) . Например, если вы хотите вычислить предел функции f(x) , где x -> 0 , то надо написать limit(f(x), x, 0) .

Также можно вычислять пределы, которые стремятся к бесконечности.

Дифференцирование

Для дифференцирования выражений в SymPy есть функция diff(func, var) . Ниже даны примеры ее работы.

Проверим результат последней функции при помощи определения производной через предел.

tan 2 (𝑥)+1 Результат тот же.

Также при помощи этой же функции могут быть вычислены производные более высоких порядков. Синтаксис функции будет следующим: diff(func, var, n) . Ниже приведено несколько примеров.

Разложение в ряд

Для разложения выражения в ряд Тейлора используется следующий синтаксис: series(expr, var) .

Интегрирование

В SymPy реализована поддержка определенных и неопределенных интегралов при помощи функции integrate() . Интегрировать можно элементарные, трансцендентные и специальные функции. Интегрирование осуществляется с помощью расширенного алгоритма Риша-Нормана. Также используются различные эвристики и шаблоны. Вот примеры интегрирования элементарных функций:

Также несложно посчитать интеграл и от специальных функций. Возьмем, например, функцию Гаусса:

Результат вычисления можете посмотреть сами. Вот примеры вычисления определенных интегралов.

Также можно вычислять определенные интегралы с бесконечными пределами интегрирования (несобственные интегралы).

Решение уравнений

При помощи SymPy можно решать алгебраические уравнения с одной или несколькими переменными. Для этого используется функция solveset() .

Как можно заметить, первое выражение функции solveset() приравнивается к 0 и решается относительно х . Также возможно решать некоторые уравнения с трансцендентными функциями.

Системы линейных уравнений

SymPy способна решать широкий класс полиномиальных уравнений. Также при помощи данной библиотеки можно решать и системы уравнений. При этом переменные, относительно которых должна быть разрешена система, передаются в виде кортежа во втором аргументе функции solve() , которая используется для таких задач.

Факторизация

Другим мощным методом исследования полиномиальных уравнений является факторизация многочленов (то есть представление многочлена в виде произведения многочленов меньших степеней). Для этого в SymPy предусмотрена функция factor() , которая способна производить факторизацию очень широкого класса полиномов.

Булевы уравнения

Также в SymPy реализована возможность решения булевых уравнений, что по сути означает проверку булевого выражения на истинность. Для этого используется функция satisfiable() .

Данный результат говорит нам о том, что выражение (x & y) будет истинным тогда и только тогда, когда x и y истинны. Если выражение не может быть истинным ни при каких значениях переменных, то функция вернет результат False .

Видео:FreeDy010 Решение Системы нелинейных уравнений scipy sympyСкачать

Линейная алгебра

Матрицы

Матрицы в SymPy создаются как экземпляры класса Matrix :

В отличие от NumPy , мы можем использовать в матрицах символьные переменные:

И производить с ними разные манипуляции:

Дифференциальные уравнения

При помощи библиотеки SymPy можно решать некоторые обыкновенные дифференциальные уравнения. Для этого используется функция dsolve() . Для начала нам надо задать неопределенную функцию. Это можно сделать, передав параметр cls=Function в функцию symbols() .

Теперь f и g заданы как неопределенные функции. мы можем в этом убедиться, просто вызвав f(x) .

Теперь решим следующее дифференциальное уравнение:

Чтобы улучшить решаемость и помочь этой функции в поиске решения, можно передавать в нее определенные ключевые аргументы. Например, если мы видим, что это уравнение с разделяемыми переменными, то мы можем передать в функцию аргумент hint=’separable’ .

Бесплатные кодинг марафоны с ревью кода

Наш телеграм канал проводит бесплатные марафоны по написанию кода на Python с ревью кода от преподавателя

Видео:Использование библиотеки SymPy для работы с символами и выражениями в PythonСкачать

Символическая математика с симпы

https://youtu.be/n_zuhuufalk Эта статья показывает, как решать математические уравнения и выражения символически, в Python. Благодаря симпы-библиотеке это оказывается чрезвычайно легкой задачей. Однако, как вы увидите в следующих примерах, количество инструментов и функций, предоставляемых этой библиотекой, огромно. Благодаря всем его функциям, Sympy … Символическая математика с симпы Подробнее »

• Автор записи

Автор: Andrea Ridolfi
Дата записи

Автор оригинала: Andrea Ridolfi.

Эта статья показывает, как решить математические уравнения и выражения символически, в Питон . Благодаря Симпи Библиотека, это оказывается чрезвычайно легкой задачей.

Однако, как вы увидите в следующих примерах, количество инструментов и функций, предоставляемых этой библиотекой, огромно. Благодаря всем его функциям, Симпи представляет собой действительно мощную систему алгебры, с которой мы можем решить Очень непосредственно, Математические выражения, уравнения, неравенства и даже Системы уравнений/неравенств Отказ

По этим причинам Симпи представляет собой фундаментальный инструмент для решения множества Математика связанные проблемы. Статья разделена на разные разделы, каждый из которых имеет дело с конкретным Симпи функция. Если вы заинтересованы в теме, вы можете найти документацию обо всех описанных здесь функциях (и много других) в https://www.sympy.org/en/index.html Отказ

Видео:Алгебра на Питоне - SymPyСкачать

Импорт Sympy

Первый шаг включает в себя импорт в наш скрипт Симпи библиотека; Поскольку несколько разных пакетов будут использоваться во всем этом примере, мы им импортируем их, написав следующую строку кода (для импорта Sympy Вы, должно быть, ранее установили его, если вы еще этого не сделали, введите « | Установить PIP Sympy » в вашем терминале).

Видео:Как решить линейное и квадратное уравнение в Python?Скачать

Определение переменных и функций

Начнем с определения переменных, которые мы хотим использовать в наших расчетах. Для этого мы эксплуатируем Симпи Функция Символы () который принимает в качестве ввода строки и превращает его в Симпи Переменная; Затем мы назначаем значение функции переменной с тем же именем выбранной строки. В следующих строках кода мы инициализируем две переменные « X » и « y ».

Аналогичная процедура может быть использована для определения имени функций, которые будут использоваться в сценарии; На этот раз S YMPY Функция, которая служит для цели, это Функция () и работает так же, как Символы () Отказ Мы, следовательно, инициализировать функцию под названием « F », с данного момента каждый раз, когда мы вводим « f » на скрипте, мы имеем в виду функцию.

Видео:the solve() Function in SymPy: Solving Equations with PythonСкачать

Использование Sympy в вашем компьютере

Симпи можно даже использовать непосредственно с вашего терминала; Именно здесь его способность символически решать математические уравнения и функции выражают все возможное. Теперь мы увидим, как инициализировать и напрямую использовать Симпи в терминале. Первое, что нужно сделать, это открыть свой терминал и импорт Симпи Аналогичным образом как и раньше. Мы, следовательно, введите «Импортировать Sympy» и нажмите Enter. После этого мы входим в следующую команду « Sympy.init_session () », следующие строки содержат две только что описанные команды и вывод, который будет предложена вашим терминалом.

Как вы можете видеть, после Sympy.init_session () Команда, несколько Симпи пакеты были импортированы; Кроме того, буквы «X», «Y», «Z» и «T» были инициализированы как симпы, «K», «M» и «n» как целочисленные параметры, в то время как буквы «F», «G» и «H» как функции.

Все эти задачи были выполнены автоматически в пределах Sympy.init_session () команда, которая в основном инициировала Симпи сеанс с некоторыми заранее определенными функциями и переменными.

Преимущество использования терминала над текстовым редактором заключается в том, что он будет представлять все функции и уравнения, используя улучшенный графический стиль, что делает их (как мы увидим) более непосредственно. Большинство команд, которые будут следовать в следующих разделах, могут быть введены как в скрипте, так и в терминале, я указываю, когда некоторые конкретные функции не будут работать на одной из двух платформ.

Видео:Solving a Second Order Differential Equation Using SympyСкачать

Расширение и упрощение математических выражений

В этом разделе мы узнаем, как использовать Симпи расширить или упростить математическое выражение. Обе задачи могут быть выполнены автоматически и мгновенно, просто используя функции Развернуть () и фактор () Отказ

Чтобы увидеть, как расширять() Функция работает, мы сначала определим функцию f = (3x + 5y 2 – 6) 2 И тогда мы передаем его как единственный входной параметр функции Развернуть () Отказ В терминале набираются следующие строки, чтобы получить лучший графический вывод; Тем не менее, они работают так же, когда набираются в скрипте.

Как вы можете увидеть из сообщенных результатов, функция Развернуть () рассчитал выражение, определенное в функции F И напечатал его усовершенствованным графическим способом, избегая звездочек и размещения показателей в качестве вершины. Представление стиля может варьироваться в зависимости от различных терминалов, но обычно его улучшается в отношении входной.

С другой стороны, функция фактор () Работает совершенно противоположным образом, он упрощает выражение, которое передается в его скобках. Вы можете увидеть пример в следующих строках.

Видео:Python для самых маленьких. Линейные уравнения. Решение задачСкачать

Решение уравнений и неравенства

Еще одна полезная функция, предлагаемая Симпи Является ли возможность найти решение алгебраических уравнений, используя функцию .решать () .

Эта функция принимает в качестве ввода двух разных параметров, уравнение, которое мы хотим решить и переменную, для которой мы хотим решить ее соответственно.

Это особенно полезно в случае символических решений уравнений с несколькими переменными, в которых нас могут быть заинтересованы в получении символического решения по одному из двух неизвестных. Следующие строки сообщают либо численное решение уравнения одного переменного и символического решения двумя переменных уравнения относительно переменной « y ».

Аналогичным образом мы также можем получить численное и/или символическое решение уравнения или неравенства высшего порядка. Оба задача отображаются в следующих строках.

Видео:СКМ-2021-05-25 SymPy Символьные вычисленияСкачать

Решение систем уравнений/неравенств

Симпи Может использоваться для решения систем уравнений/неравенств. Для этого мы будем эксплуатировать, снова функции решить () Отказ В случае системы уравнений мы вводим уравнения в виде элементов списка; Следующие строки описывают решение системы трех линейных уравнений с помощью решить () Отказ

Как видно, вывод решить () Функция – это значения трех разных системных переменных. Таким же образом, мы также можем получить решение систем неравенств; Достаточно ввести неравенства как элементы списка; На этот раз символы «>» Метки

Видео:Решение системы уравнений 5 вариантов Python, SymPy, linsolve() #shorts, #pythonshorts, #codeshortsСкачать

Символьное решение линейных дифференциальных уравнений и систем методом преобразований Лапласа c применением SymPy

Реализация алгоритмов на языке Python с использованием символьных вычислений очень удобна при решении задач математического моделирования объектов, заданных дифференциальными уравнениями. Для решения таких уравнений широко используются преобразования Лапласа, которые, говоря упрощенно, позволяют свести задачу к решению простейших алгебраических уравнений.

В данной публикации предлагаю рассмотреть функции прямого и обратного преобразования Лапласа из библиотеки SymPy, которые позволяют использовать метод Лапласа для решения дифференциальных уравнений и систем средствами Python.

Сам метод Лапласа и его преимущества при решении линейных дифференциальных уравнений и систем широко освещены в литературе, например в популярном издании [1]. В книге метод Лапласа приведен для реализации в лицензионных программных пакетах Mathematica, Maple и MATLAB (что подразумевает приобретение учебным заведением этого ПО) на выбранных автором отдельных примерах.

Попробуем сегодня рассмотреть не отдельный пример решения учебной задачи средствами Python, а общий метод решения линейных дифференциальных уравнений и систем с использованием функций прямого и обратного преобразования Лапласа. При этом сохраним обучающий момент: левая часть линейного дифференциального уравнения с условиями Коши будет формироваться самим студентом, а рутинная часть задачи, состоящая в прямом преобразовании Лапласа правой части уравнения, будет выполняться при помощи функции laplace_transform().

История об авторстве преобразований Лапласа

Преобразования Лапласа (изображения по Лапласу) имеют интересную историю. Впервые интеграл в определении преобразования Лапласа появился в одной из работ Л. Эйлера. Однако в математике общепринято называть методику или теорему именем того математика, который открыл ее после Эйлера. В противном случае существовало бы несколько сотен различных теорем Эйлера.

В данном случае следующим после Эйлера был французский математик Пьер Симон де Лаплас (Pierre Simon de Laplace (1749-1827)). Именно он использовал такие интегралы в своей работе по теории вероятностей. Самим Лапласом не применялись так называемые «операционные методы» для нахождения решений дифференциальных уравнений, основанные на преобразованиях Лапласа (изображениях по Лапласу). Эти методы в действительности были обнаружены и популяризировались инженерами-практиками, особенно английским инженером-электриком Оливером Хевисайдом (1850-1925). Задолго до того, как была строго доказана справедливость этих методов, операционное исчисление успешно и широко применялось, хотя его законность ставилось в значительной мере под сомнение даже в начале XX столетия, и по этой теме велись весьма ожесточенные дебаты.

Функции прямого и обратного преобразования Лапласа

Эта функция возвращает (F, a, cond), где F(s) есть преобразование Лапласа функции f(t), a Текст программы

Время на обратное визуальное преобразование Лапласа: 2.68 s

Обратное преобразование Лапласа часто используется при синтезе САУ, где Python может заменить дорогостоящих программных “монстров” типа MathCAD, поэтому приведенное использование обратного преобразования имеет практическое значение.

Преобразование Лапласа от производных высших порядков для решения задачи Коши

Если a и b — константы, то

для всех s, таких, что существуют оба преобразования Лапласа (изображения по Лапласу) функций f(t) и q(t).

Проверим линейность прямого и обратного преобразований Лапласа с помощью ранее рассмотренных функций laplace_transform() и inverse_laplace_transform(). Для этого в качестве примера примем f(t)=sin(3t), q(t)=cos(7t), a=5, b=7 и используем следующую программу.

(7*s**3 + 15*s**2 + 63*s + 735)/((s**2 + 9)*(s**2 + 49))
(7*s**3 + 15*s**2 + 63*s + 735)/((s**2 + 9)*(s**2 + 49))
True
5*sin(3*t) + 7*cos(7*t)
5*sin(3*t) + 7*cos(7*t)

Приведенный код также демонстрирует однозначность обратного преобразования Лапласа.

Если предположить, что удовлетворяет условиям первой теоремы, то из этой теоремы будет следовать, что:

Повторение этого вычисления дает

После конечного числа таких шагов мы получаем следующее обобщение первой теоремы:

Применяя соотношение (3), содержащее преобразованные по Лапласу производные искомой функции с начальными условиями, к уравнению (1), можно получить его решение по методу, специально разработанному на нашей кафедре при активной поддержке Scorobey для библиотеки SymPy.

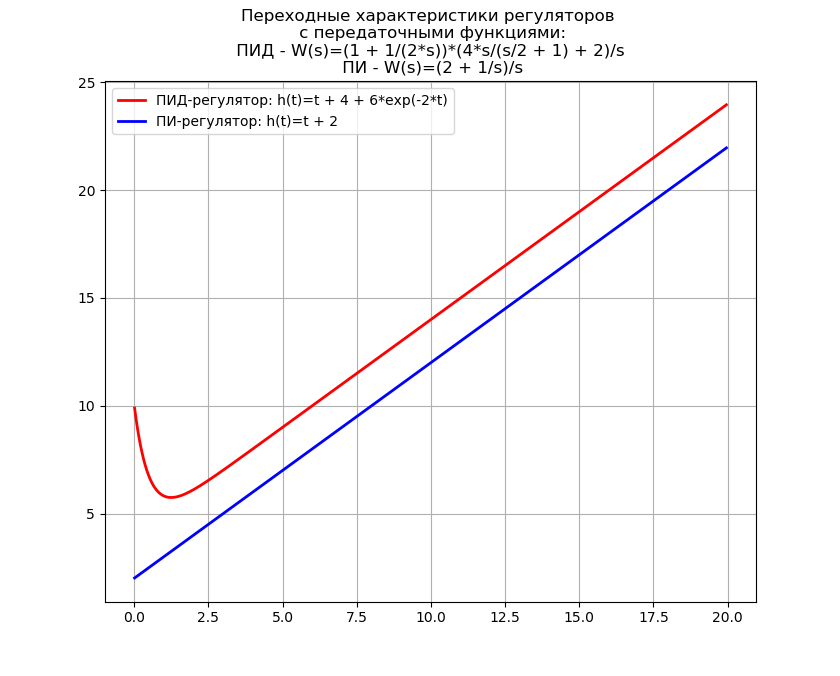
Метод решения линейных дифференциальных уравнений и систем уравнений, основанный на преобразованиях Лапласа, с использованием библиотеки SymPy

где — приведенное начальное положение массы, — приведенная начальная скорость массы.

Упрощённая физическая модель, заданная уравнением (4) при ненулевых начальных условиях [1]:

Система, состоящая из материальной точки заданной массы, закрепленной на пружине, удовлетворяет задаче Коши (задаче с начальными условиями). Материальная точка заданной массы первоначально находится в покое в положении ее равновесия.

Для решения этого и других линейных дифференциальных уравнений методом преобразований Лапласа удобно пользоваться следующей системой, полученной из соотношений (3):

Последовательность решения средствами SymPy следующая:

загружаем необходимые модули и явно определяем символьные переменные:

указываем версию библиотеки sympy, чтобы учесть ее особенности. Для этого нужно ввести такие строки:

по физическому смыслу задачи переменная времени определяется для области, включающей ноль и положительные числа. Задаём начальные условия и функцию в правой части уравнения (4) с её последующим преобразование по Лапласу. Для начальных условий необходимо использовать функцию Rational, поскольку использование десятичного округления приводит к ошибке.

пользуясь (5), переписываем преобразованные по Лапласу производные, входящие в левую часть уравнения (4), формируя из них левую часть этого уравнения, и сравниваем результат с правой его частью:

решаем полученное алгебраическое уравнение относительно преобразования X(s) и выполняем обратное преобразование Лапласа:

осуществляем переход из работы в библиотеке SymPyв библиотеку NumPy:

строим график обычным для Python методом:

Получаем:
Версия библиотеки sympy – 1.3

Получен график периодической функции, дающей положение материальной точки заданной массы. Метод преобразования Лапласа с использованием библиотеки SymPy дает решение не только без потребности сначала найти общее решение однородного уравнения и частное решение первоначального неоднородного дифференциального уравнения, но и без потребности использования метода элементарных дробей и таблиц Лапласа.

При этом учебное значение метода решения сохраняется за счёт необходимости использования системы (5) и перехода в NumPy для исследования решения более производительными методами.

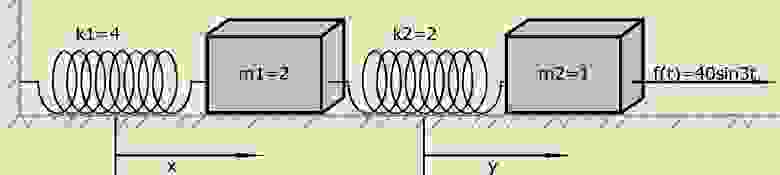
Для дальнейшей демонстрации метода решим систему дифференциальных уравнений:

с начальными условиями

Упрощённая физическая модель, заданная системой уравнений (6) при нулевых начальных условиях:

Таким образом, сила f(t) внезапно прилагается ко второй материальной точке заданной массы в момент времени t = 0, когда система находится в покое в ее положении равновесия.

Решение системы уравнений идентично ранее рассмотренному решению дифференциального уравнения (4), поэтому привожу текст программы без пояснений.

Для ненулевых начальных условий текст программы и график функций примет вид:

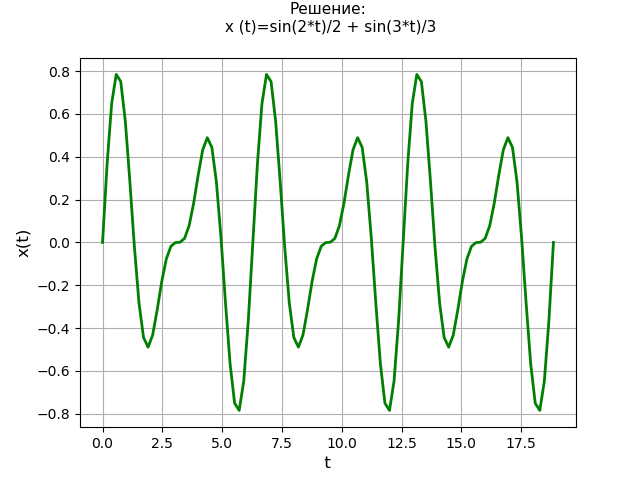
Рассмотрим решение линейного дифференциального уравнения четвёртого порядка с нулевыми начальными условиями:

Решим линейное дифференциальное уравнение четвёртого порядка:

с начальными условиями , , .

Функции для решения ОДУ

Для имеющих аналитическое решение ОДУ и систем ОДУ применяется функция dsolve():
sympy.solvers.ode.dsolve(eq, func=None, hint=’default’, simplify=True, ics=None, xi=None, eta=None, x0=0, n=6, **kwargs)

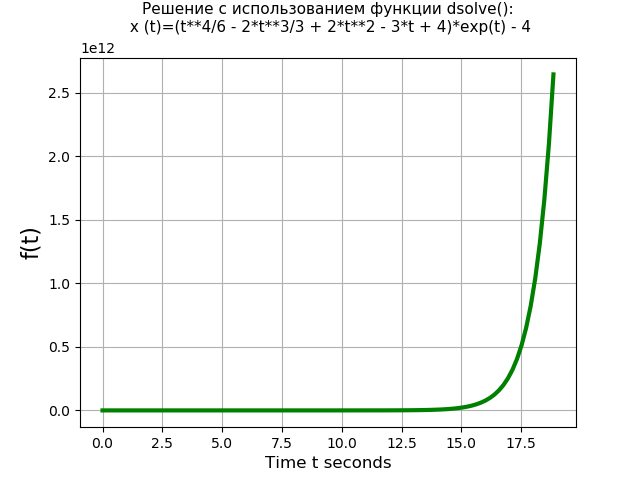
Давайте сравним производительность функции dsolve() с методом Лапласа. Для примера возьмём следующее дифференциальное уравнение четвёртой степени с нулевыми начальными условиями:

Время решения уравнения с использованием функции dsolve(): 1.437 s

Время решения уравнения с использованием преобразования Лапласа: 3.274 s

Итак, функция dsolve() (1.437 s) решает уравнение четвёртого порядка быстрее, чем выполняется решение по методу преобразований Лапласа (3.274 s) более чем в два раза. Однако при этом следует отметить, что функция dsolve() не решает системы дифференциальных уравнений второго порядка, например, при решении системы (6) с использованием функция dsolve() возникает ошибка:

Данная ошибка означает, что решение системы дифференциальных уравнений с помощью функции dsolve() не может быть представлено символьно. Тогда как при помощи преобразований Лапласа мы получили символьное представление решения, и это доказывает эффективность предложенного метода.

Для того чтобы найти необходимый метод решения дифференциальных уравнений с помощью функции dsolve(), нужно использовать classify_ode(eq, f(x)), например:

Eq(f(x), C1*sin(x) + C2*cos(x))
(‘nth_linear_constant_coeff_homogeneous’, ‘2nd_power_series_ordinary’)
(‘separable’, ‘1st_exact’, ‘almost_linear’, ‘1st_power_series’, ‘lie_group’, ‘separable_Integral’, ‘1st_exact_Integral’, ‘almost_linear_Integral’)
[Eq(f(x), -acos((C1 + Integral(0, x))*exp(-Integral(-tan(x), x))) + 2*pi), Eq(f(x), acos((C1 + Integral(0,x))*exp(-Integral(-tan(x), x))))]

Таким образом, для уравнения eq=Eq(f(x).diff(x,x)+f(x),0) работает любой метод из первого списка:

Для уравнения eq = sin(x)*cos(f(x)) + cos(x)*sin(f(x))*f(x).diff(x) работает любой метод из второго списка:

separable, 1st_exact, almost_linear,
1st_power_series, lie_group, separable_Integral,
1st_exact_Integral, almost_linear_Integral

Чтобы использовать выбранный метод, запись функции dsolve() примет вид, к примеру:

Вывод:

Данная статья ставила своей целью показать, как использовать средства библиотек SciPy и NumPy на примере решения систем линейных ОДУ операторным методом. Таким образом, были рассмотрены методы символьного решения линейных дифференциальных уравнений и систем уравнений методом Лапласа. Проведен анализ производительности этого метода и методов, реализованных в функции dsolve().

1. Дифференциальные уравнения и краевые задачи: моделирование и вычисление с помощью Mathematica, Maple и MATLAB. 3-е издание.: Пер. с англ. — М.: ООО «И.Д. Вильяме», 2008. — 1104 с.: ил. — Парал. тит. англ.
2. Использование обратного преобразования Лапласа для анализа динамических звеньев систем управления

🌟 Видео

СЛАУ в PythonСкачать

Решение n го нелинейных алгебраических уравнений в PythonСкачать

Будет день и будет код! SymPy откройся! Видео 3. #Python, #SymPy, #Eq ,#exp, #solveset, #linsolveСкачать

Solving a Differential Equation with Python & SymPyСкачать

Решение систем линейных матричных уравнений через формулы Крамера в PythonСкачать