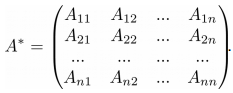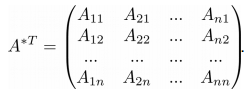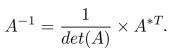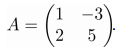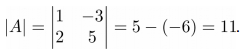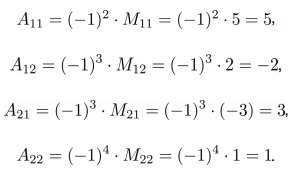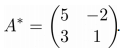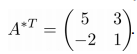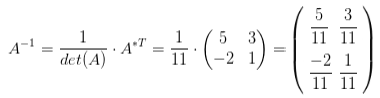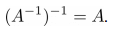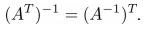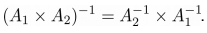Решение линейных уравнений методом обратной матрицы питон

Библиотеку Numpy можно использовать для выполнения множества математических и научных операций, таких как скалярное произведение, поиск значений синуса и косинуса, преобразование Фурье и т.д.

Видео:Решение системы уравнений методом обратной матрицы - bezbotvyСкачать

Что такое система линейных уравнений?

Википедия определяет систему линейных уравнений как:

В математике система линейных уравнений (или линейная система) – это набор двух или более линейных уравнений, включающих один и тот же набор переменных.

Конечная цель решения системы линейных уравнений – найти значения неизвестных переменных. Вот пример системы линейных уравнений с двумя неизвестными переменными x и y:

Чтобы решить указанную выше систему линейных уравнений, нам нужно найти значения переменных x и y. Есть несколько способов решить такую систему, например, исключение переменных, правило Крамера, метод сокращения строк и матричное решение.

В матричном решении решаемая система линейных уравнений представлена в виде матрицы AX = B. Например, мы можем представить уравнение 1 в виде матрицы следующим образом:

Чтобы найти значение переменных x и y в уравнении 1, нам нужно найти значения в матрице X. Для этого мы можем взять скалярное произведение обратной матрицы A и матрицы B, как показано ниже:

Если вы не знакомы с тем, как найти обратную матрицу, взгляните на эту ссылку, чтобы понять, как вручную найти обратную матрицу.

Видео:Решение системы уравнений методом обратной матрицы.Скачать

Решение

Из предыдущего раздела мы знаем, что для решения системы линейных уравнений нам необходимо выполнить две операции: обращение и скалярное произведение матрицы. Библиотека Numpy от Python поддерживает обе операции. Если вы еще не установили библиотеку Numpy, вы можете сделать это с помощью следующей команды pip:

Давайте теперь посмотрим, как решить систему линейных уравнений с помощью библиотеки Numpy.

Видео:Система линейных уравнений. Метод обратной матрицы. Матричный метод.Скачать

Использование методов inv() и dot()

Сначала мы найдем матрицу, обратную матрице A, которую мы определили в предыдущем разделе.

Давайте сначала создадим матрицу A на Python. Для создания матрицы можно использовать метод массива модуля Numpy. Матрицу можно рассматривать как список списков, где каждый список представляет собой строку.

В следующем скрипте мы создаем список с именем m_list, который дополнительно содержит два списка: [4,3] и [-5,9]. Эти списки представляют собой две строки в матрице A. Чтобы создать матрицу A с помощью Numpy, m_list передается методу массива, как показано ниже:

Чтобы найти обратную матрицу, которая передается методу linalg.inv() модуля Numpy:

Следующим шагом является нахождение скалярного произведения между матрицей, обратной матрицей A и B. Важно отметить, что матричное скалярное произведение возможно только между матрицами, если их внутренние размеры равны, т.е. количество столбцов левой матрицы должно соответствовать количеству строк в правой матрице.

Чтобы найти точечный продукт с помощью библиотеки Numpy, используется функция linalg.dot(). Следующий скрипт находит скалярное произведение между обратной матрицей A и B, которая является решением уравнения 1.

Здесь 2 и 4 – соответствующие значения для неизвестных x и y в уравнении 1. Чтобы убедиться, что если вы подставите 2 вместо неизвестного x и 4 вместо неизвестного y в уравнении 4x + 3y, вы увидите что результат будет 20.

Давайте теперь решим систему трех линейных уравнений, как показано ниже:

Вышеупомянутое уравнение можно решить с помощью библиотеки Numpy следующим образом:

В приведенном выше скрипте методы linalg.inv() и linalg.dot() связаны вместе. Переменная X содержит решение уравнения 2 и печатается следующим образом:

Значения неизвестных x, y и z равны 5, 3 и -2 соответственно. Вы можете подставить эти значения в уравнение 2 и проверить их правильность.

Видео:11. Решение систем линейных уравнений методом обратной матрицы (матричный метод)Скачать

resolve()

В двух предыдущих примерах мы использовали методы linalg.inv() и linalg.dot() для поиска решения системы уравнений. Однако библиотека Numpy содержит метод linalg.solve(), который можно использовать для непосредственного поиска решения системы линейных уравнений:

Вы можете видеть, что результат такой же, как и раньше.

Видео:СЛАУ в PythonСкачать

Пример

Давайте посмотрим, как систему линейных уравнений можно использовать для решения реальных задач.

Предположим, продавец фруктов продал 20 манго и 10 апельсинов за один день на общую сумму 350 долларов. На следующий день он продал 17 манго и 22 апельсина за 500 долларов. Если цены на фрукты оставались неизменными в оба дня, какова была цена одного манго и одного апельсина?

Эту задачу легко решить с помощью системы двух линейных уравнений.

Допустим, цена одного манго равна x, а цена апельсина – y. Вышеупомянутую проблему можно преобразовать так:

Решение для указанной выше системы уравнений показано здесь:

И вот результат:

Выходные данные показывают, что цена одного манго составляет 10 долларов, а цена одного апельсина – 15 долларов.

Видео:9. Метод обратной матрицы для решения систем линейных уравнений / матричный методСкачать

Решение систем линейных уравнений с помощью Python’s Numpy

Два или более линейных уравнения с одинаковым набором переменных называются системой линейных уравнений. Мы можем решить эти переменные в Python с помощью Numpy.

• Автор записи

Автор: Guest Contributor
Дата записи

Библиотека Numpy может использоваться для выполнения различных математических/научных операций, таких как матричные кросс-и точечные произведения, поиск значений синуса и косинуса, преобразование Фурье и манипулирование формой и т. Д. Слово Numpy-это сокращенное обозначение “Числового питона”.

В этой статье вы увидите, как решить систему линейных уравнений с помощью библиотеки Numpy Python.

Что такое Система линейных уравнений?

В математике система линейных уравнений (или линейная система) представляет собой совокупность двух или более линейных уравнений, включающих один и тот же набор переменных.

Конечная цель решения системы линейных уравнений – найти значения неизвестных переменных. Вот пример системы линейных уравнений с двумя неизвестными переменными, x и y :

Чтобы решить приведенную выше систему линейных уравнений, нам нужно найти значения переменных x и y . Существует множество способов решения такой системы, таких как Исключение переменных, Правило Крамера, Метод сокращения строк и Матричное решение. В этой статье мы рассмотрим матричное решение.

В матричном решении система решаемых линейных уравнений представляется в виде матрицы AX . Например, мы можем представить Уравнение 1 в виде матрицы следующим образом:

Чтобы найти значение переменных x и y в Уравнение 1 , нам нужно найти значения в матрице X . Для этого мы можем взять точечное произведение обратной матрицы A и матрицы B , как показано ниже:

Если вы не знакомы с тем, как найти обратную матрицу, взгляните на эту ссылку, чтобы понять, как вручную найти обратную матрицу. Чтобы понять матричный точечный продукт, ознакомьтесь с этой статьей .

Решение системы линейных уравнений с Numpy

Из предыдущего раздела мы знаем, что для решения системы линейных уравнений необходимо выполнить две операции: инверсию матрицы и матричное точечное произведение. Библиотека Numpy из Python поддерживает обе эти операции. Если вы еще не установили библиотеку Numpy, вы можете сделать это с помощью следующей команды pip :

Теперь давайте посмотрим, как решить систему линейных уравнений с помощью библиотеки Numpy.

Использование методов inv() и dot()

Во-первых, мы найдем обратную матрицу A , которую мы определили в предыдущем разделе.

Давайте сначала создадим матрицу A в Python. Для создания матрицы можно использовать метод array модуля Numpy. Матрицу можно рассматривать как список списков, где каждый список представляет собой строку.

В следующем скрипте мы создаем список с именем m_list , который далее содержит два списка: [4,3] и [-5,9] . Эти списки являются двумя строками в матрице A . Чтобы создать матрицу A с помощью Numpy, m_list передается методу array , как показано ниже:

Чтобы найти обратную матрицу, матрица передается в метод linalg.inv() модуля Numpy:

Следующий шаг-найти точечное произведение между обратной матрицей A и матрицей B . Важно отметить, что матричное точечное произведение возможно только между матрицами , если внутренние размеры матриц равны , то есть количество столбцов левой матрицы должно соответствовать количеству строк в правой матрице.

Для поиска точечного продукта с помощью библиотеки Numpy используется функция linalg.dot () . Следующий скрипт находит точечное произведение между обратной матрицей A и матрицей B , которая является решением уравнения 1 .

Вот, 2 и 4 являются ли соответствующие значения для неизвестных x и y in Уравнение 1 . Для проверки, если вы подключаете 2 на месте неизвестного x и 4 на месте неизвестного y в уравнении 4x + 3y вы увидите , что результат будет равен 20.

Давайте теперь решим систему из трех линейных уравнений, как показано ниже:

Приведенное выше уравнение можно решить с помощью библиотеки Numpy следующим образом:

В приведенном выше скрипте методы linalg.inv() и linalg.dot() соединены вместе. Переменная X содержит решение для уравнения 2 и печатается следующим образом:

Значение для неизвестных x , y и z равно 5, 3 и -2 соответственно. Вы можете подключить эти значения в Уравнение 2 и проверить их правильность.

Использование метода solve()

В предыдущих двух примерах мы использовали методы linalg.inv() и linalg.dot() для нахождения решения системы уравнений. Однако библиотека Numpy содержит метод linalg.dsolve () , который может быть использован для непосредственного нахождения решения системы линейных уравнений:

Вы можете видеть, что выход такой же, как и раньше.

Реальный Пример

Давайте посмотрим, как система линейных уравнений может быть использована для решения реальных задач.

Предположим, продавец фруктов продал 20 манго и 10 апельсинов за один день на общую сумму 350 долларов. На следующий день он продал 17 манго и 22 апельсина за 500 долларов. Если цены на фрукты оставались неизменными в оба дня, то какова была цена одного манго и одного апельсина?

Эта задача легко решается с помощью системы двух линейных уравнений.

Допустим, цена одного манго равна x , а цена одного апельсина равна y . Вышеприведенная проблема может быть преобразована следующим образом:

Решение приведенной выше системы уравнений показано здесь:

Результат показывает, что цена одного манго составляет 10 долларов, а цена одного апельсина-15 долларов.

Видео:Матричный метод решения систем линейных уравнений (метод обратной матрицы)Скачать

Линейная алгебра на Python. [Урок 5]. Обратная матрица и ранг матрицы

Пятый урок посвящен нахождению обратной матрицы, ее свойствам, а также определению ранга матрицы

Видео:Матричный метод решения систем уравненийСкачать

Обратная матрица

Обратной матрицей A -1 матрицы A называют матрицу, удовлетворяющую следующему равенству:

Видео:Линейная алгебра, 5 урок, Обратная матрицаСкачать

где – E это единичная матрица.

Для того, чтобы у квадратной матрицы A была обратная матрица необходимо и достаточно чтобы определитель |A| был не равен нулю. Введем понятие союзной матрицы . Союзная матрица A* строится на базе исходной A путем замены всех элементов матрицы A на их алгебраические дополнения.

Видео:Метод обратной матрицы решения систем линейных уравненийСкачать

Союзная ей матрица A*:

Транспонируя матрицу A*, мы получим так называемую присоединенную матрицу A* T :

Теперь, зная как вычислять определитель и присоединенную матрицу, мы можем определить матрицу A -1 , обратную матрице A:

Видео:Excel метод обратной матрицыСкачать

Пример вычисления обратной матрицы. Пусть дана исходная матрица A, следующего вида:

Для начала найдем определитель матрицы A:

Как видно из приведенных вычислений, определитель матрицы не равен нулю, значит у матрицы A есть обратная. Построим присоединенную матрицу, для этого вычислим алгебраические дополнения для каждого элемента матрицы A:

Союзная матрица будет иметь следующий вид:

Присоединенная матрица получается из союзной путем транспонирования:

Находим обратную матрицу:

➤ Пример на Python

Решим задачу определения обратной матрицы на Python. Для получения обратной матрицы будем использовать функцию inv():

Рассмотрим свойства обратной матрицы.

Свойство 1 . Обратная матрица обратной матрицы есть исходная матрица:

➤Пример на Python

Свойство 2 . Обратная матрица транспонированной матрицы равна транспонированной матрице от обратной матрицы:

➤ Пример на Python

Свойство 3 . Обратная матрица произведения матриц равна произведению обратных матриц:

➤ Пример на Python

Видео:Обратная матрицаСкачать

Ранг матрицы

Ранг матрицы является еще одной важной численной характеристикой. Рангом называют максимальное число линейно независимых строк (столбцов) матрицы. Линейная независимость означает, что строки (столбцы) не могут быть линейно выражены через другие строки (столбцы). Ранг матрицы можно найти через ее миноры, он равен наибольшему порядку минора, который не равен нулю. Существование ранга у матрицы не зависит от того квадратная она или нет.

Вычислим ранг матрицы с помощью Python. Создадим единичную матрицу:

Ранг такой матрицы равен количеству ее столбцов (или строк), в нашем случае ранг будет равен четырем, для его вычисления на Python воспользуемся функцией matrix_rank():

Если мы приравняем элемент в нижнем правом углу к нулю, то ранг станет равен трем:

Видео:Решение системы линейных алгебраических уравнений (СЛАУ) в Excel МАТРИЧНЫМ МЕТОДОМСкачать

P.S.

Вводные уроки по “Линейной алгебре на Python” вы можете найти соответствующей странице нашего сайта . Все уроки по этой теме собраны в книге “Линейная алгебра на Python”.

Если вам интересна тема анализа данных, то мы рекомендуем ознакомиться с библиотекой Pandas. Для начала вы можете познакомиться с вводными уроками. Все уроки по библиотеке Pandas собраны в книге “Pandas. Работа с данными”.

Видео:Как находить обратную матрицу - bezbotvyСкачать

Линейная алгебра на Python. [Урок 5]. Обратная матрица и ранг матрицы : 1 комментарий

i want that help me
1) написать программу вычисляющую обратную матрицу

2) написать программу для решения СЛАУ с помощью обратной матрицы

3) сравнить скорость работы всех трёх методов решения СЛАУ

🎬 Видео

Метод Крамера за 3 минуты. Решение системы линейных уравнений - bezbotvyСкачать

Обратная матрица (2 способа нахождения)Скачать

Математика без Ху!ни. Метод Гаусса.Скачать

Линейная алгебра, 7 урок, СЛАУ. Матричный методСкачать

6 способов в одном видеоСкачать

8. Обратная матрицаСкачать