Дана система 

Формально задача ставится следующим образом: решить систему:
где коэффициенты 


Удобно матричное представление этой задачи:
где 
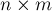




Стоит отметить, что СЛАУ может быть не над полем действительных чисел, а над полем по модулю какого-либо числа 
— алгоритм Гаусса работает и для таких систем тоже (но этот случай будет рассмотрен ниже в отдельном разделе).
- Алгоритм Гаусса
- Базовая схема
- Поиск опорного элемента (pivoting)
- Вырожденные случаи
- Реализация
- Асимптотика
- Более точная оценка числа действий
- Дополнения
- Ускорение алгоритма: разделение его на прямой и обратный ход
- Решение СЛАУ по модулю
- Немного о различных способах выбора опорного элемента
- Улучшение найденного ответа
- Метод Гаусса на Java
- Теоретические сведения
- Реализация
- Вывод
- Параллельное решение систем линейных уравнений.
- Цель лабораторной работы
- Введение
- Изучение последовательного алгоритма Гаусса решения систем линейных уравнений
- Построение параллельного алгоритма решения методом Гаусса
- Анализ эффективности параллельных вычислений метода Гаусса
- Заключение
- 📸 Видео
Видео:Решение системы уравнений методом Гаусса 4x4Скачать

Алгоритм Гаусса
Строго говоря, описываемый ниже метод правильно называть методом «Гаусса-Жордана» (Gauss-Jordan elimination), поскольку он является вариацией метода Гаусса, описанной геодезистом Вильгельмом Жорданом в 1887 г. (стоит отметить, что Вильгельм Жордан не является автором ни теоремы Жордана о кривых, ни жордановой алгебры — всё это три разных учёных-однофамильца; кроме того, по всей видимости, более правильной является транскрипция «Йордан», но написание «Жордан» уже закрепилось в русской литературе). Также интересно заметить, что одновременно с Жорданом (а по некоторым данным даже раньше него) этот алгоритм придумал Класен (B.-I. Clasen).
Базовая схема
Кратко говоря, алгоритм заключается в последовательном исключении переменных из каждого уравнения до тех пор, пока в каждом уравнении не останется только по одной переменной. Если 

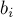
При этом алгоритм основывается на двух простых эквивалентных преобразованиях системы: во-первых, можно обменивать два уравнения, а во-вторых, любое уравнение можно заменить линейной комбинацией этой строки (с ненулевым коэффициентом) и других строк (с произвольными коэффициентами).
На первом шаге алгоритм Гаусса-Жордана делит первую строку на коэффициент 






В итоге, по окончании первого шага первый столбец матрицы 
Аналогично производится второй шаг алгоритма, только теперь рассматривается второй столбец и вторая строка: сначала вторая строка делится на 

И так далее, пока мы не обработаем все строки или все столбцы матрицы 


Поиск опорного элемента (pivoting)
Разумеется, описанная выше схема неполна. Она работает только в том случае, если на каждом 


Чтобы сделать алгоритм работающим в таких случаях, как раз и существует процесс выбора опорного элемента (на английском языке это называется одним словом «pivoting»). Он заключается в том, что производится перестановка строк и/или столбцов матрицы, чтобы в нужном элементе 
Заметим, что перестановка строк значительно проще реализуется на компьютере, чем перестановка столбцов: ведь при обмене местами двух каких-то столбцов надо запомнить, что эти две переменных обменялись местами, чтобы затем, при восстановлении ответа, правильно восстановить, какой ответ к какой переменной относится. При перестановке строк никаких таких дополнительных действий производить не надо.
К счастью, для корректности метода достаточно одних только обменов строк (т.н. «partial pivoting», в отличие от «full pivoting», когда обмениваются и строки, и столбцы). Но какую же именно строку следует выбирать для обмена? И правда ли, что поиск опорного элемента надо делать только тогда, когда текущий элемент 
Общего ответа на этот вопрос не существует. Есть разнообразные эвристики, однако самой эффективной из них (по соотношению простоты и отдачи) является такая эвристика: в качестве опорного элемента следует брать наибольший по модулю элемент, причём производить поиск опорного элемента и обмен с ним надо всегда, а не только когда это необходимо (т.е. не только тогда, когда 
Иными словами, перед выполнением 




Во-первых, эта эвристика позволит решить СЛАУ, даже если по ходу решения будет случаться так, что элемент 
Без этой эвристики, даже если система такова, что на каждой 


Вырожденные случаи
Итак, если останавливаться на алгоритме Гаусса-Жордана с partial pivoting, то, утверждается, если 

Рассмотрим теперь общий случай — когда 






Итак, некоторые переменные в процессе работы алгоритма могут оказываться независимыми. Понятно, что когда количество 


В целом, если обнаружилась хотя бы одна независимая переменная, то она может принимать произвольное значение, в то время как остальные (зависимые) переменные будут выражаться через неё. Это означает, что, когда мы работаем в поле действительных чисел, система потенциально имеет бесконечно много решений (если мы рассматриваем СЛАУ по модулю, то число решений будет равно этому модулю в степени количества независимых переменных). Впрочем, следует быть аккуратным: надо помнить о том, что даже если были обнаружены независимые переменные, тем не менее СЛАУ может не иметь решений вовсе. Это происходит, когда в оставшихся необработанными уравнениях (тех, до которых алгоритм Гаусса-Жордана не дошёл, т.е. это уравнения, в которых остались только независимые переменные) есть хотя бы один ненулевой свободный член.
Впрочем, проще это проверить явной подстановкой найденного решения: всем независимыми переменным присвоить нулевые значения, зависимым переменным присвоить найденные значения, и подставить это решение в текущую СЛАУ.
Видео:Решение системы уравнений методом ГауссаСкачать

Реализация
Приведём здесь реализацию алгоритма Гаусса-Жордана с эвристикой partial pivoting (выбором опорного элемента как максимума по столбцу).
На вход функции 





Функция возвращает число решений системы (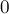

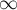


В функции поддерживаются два указателя — на текущий столбец 

Также заводится вектор 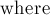
Реализация использует технику partial pivoting, производя поиск строки с максимальным по модулю элементом, и переставляя затем эту строку в позицию 
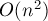
В реализации в целях простоты текущая строка не делится на опорный элемент — так что в итоге по окончании работы алгоритма матрица становится не единичной, а диагональной (впрочем, по-видимому, деление строки на ведущий элемент позволяет несколько уменьшить возникающие погрешности).
После нахождения решения оно подставляется обратно в матрицу — чтобы проверить, имеет ли система хотя бы одно решение или нет. Если проверка найденного решения прошла успешно, то функция возвращает 
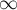
Видео:Решение системы линейных уравнений методом ГауссаСкачать

Асимптотика
Оценим асимптотику полученного алгоритма. Алгоритм состоит из 
- поиск и перестановка опорного элемента — за время
при использовании эвристики «partial pivoting» (поиск максимума в столбце)
- если опорный элемент в текущем столбце был найден — то прибавление текущего уравнения ко всем остальным уравнениям — за время
Очевидно, первый пункт имеет меньшую асимптотику, чем второй. Заметим также, что второй пункт выполняется не более 
Таким образом, итоговая асимптотика алгоритма принимает вид 
При 
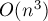
Заметим, что когда СЛАУ рассматривается не в поле действительных чисел, а в поле по модулю два, то систему можно решать гораздо быстрее — об этом см. ниже в разделе «Решение СЛАУ по модулю».
Более точная оценка числа действий
Для простоты выкладок будем считать, что 
Как мы уже знаем, время работы всего алгоритма фактически определяется временем, затрачиваемым на исключение текущего уравнения из остальных.
Это может происходить на каждом из 
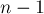

Видео:Решение систем линейных уравнений, урок 4/5. Метод ГауссаСкачать

Дополнения
Ускорение алгоритма: разделение его на прямой и обратный ход
Добиться двукратного ускорения алгоритма можно, рассмотрев другую его версию, более классическую, когда алгоритм разбивается на фазы прямого и обратного хода.
В целом, в отличие от описанного выше алгоритма, можно приводить матрицу не к диагональному виду, а к треугольному виду — когда все элементы строго ниже главной диагонали равны нулю.
Система с треугольной матрицей решается тривиально — сначала из последнего уравнения сразу находится значение последней переменной, затем найденное значение подставляется в предпоследнее уравнение и находится значение предпоследней переменной, и так далее. Этот процесс и называется обратным ходом алгоритма Гаусса.
Прямой ход алгоритма Гаусса — это алгоритм, аналогичный описанному выше алгоритму Гаусса-Жордана, за одним исключением: текущая переменная исключается не из всех уравнений, а только из уравнений после текущего. В результате этого действительно получается не диагональная, а треугольная матрица.
Разница в том, что прямой ход работает быстрее алгоритма Гаусса-Жордана — поскольку в среднем он делает в два раза меньше прибавлений одного уравнения к другому. Обратный ход работает за 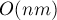
Таким образом, если 

Решение СЛАУ по модулю
Для решения СЛАУ по модулю можно применять описанный выше алгоритм, он сохраняет свою корректность.
Разумеется, теперь становится ненужным использовать какие-то хитрые техники выбора опорного элемента — достаточно найти любой ненулевой элемент в текущем столбце.
Если модуль простой, то никаких сложностей вообще не возникает — происходящие по ходу работы алгоритма Гаусса деления не создают особых проблем.
Особенно замечателен модуль, равный двум: для него все операции с матрицей можно производить очень эффективно. Например, отнимание одной строки от другой по модулю два — это на самом деле их симметрическая разность («xor»). Таким образом, весь алгоритм можно значительно ускорить, сжав всю матрицу в битовые маски и оперируя только ими. Приведём здесь новую реализацию основной части алгоритма Гаусса-Жордана, используя стандартный контейнер C++ «bitset»:
Как можно заметить, реализация стала даже немного короче, при том, что она значительно быстрее старой реализации — а именно, быстрее в 
Если модуль произвольный (не обязательно простой), то всё становится несколько сложнее. Понятно, что пользуясь Китайской теоремой об остатках, мы сводим задачу с произвольным модулем только к модулям вида «степень простого». [ дальнейший текст был скрыт, т.к. это непроверенная информация — возможно, неправильный способ решения ]
Наконец, рассмотрим вопрос числа решений СЛАУ по модулю. Ответ на него достаточно прост: число решений равно 


Немного о различных способах выбора опорного элемента
Как уже говорилось выше, однозначного ответа на этот вопрос нет.
Эвристика «partial pivoting», которая заключалась в поиске максимального элемента в текущем столбце, работает на практике весьма неплохо. Также оказывается, что она даёт практически тот же результат, что и «full pivoting» — когда опорный элемент ищется среди элементов целой подматрицы — начиная с текущей строки и с текущего столбца.
Но интересно отметить, что обе эти эвристики с поиском максимального элемента, фактически, очень зависят от того, насколько были промасштабированы исходные уравнения. Например, если одно из уравнений системы умножить на миллион, то это уравнение почти наверняка будет выбрано в качестве ведущего на первом же шаге. Это кажется достаточно странным, поэтому логичен переход к немного более сложной эвристике — так называемому «implicit pivoting».
Эвристика implicit pivoting заключается в том, что элементы различных строк сравниваются так, как если бы обе строки были пронормированы таким образом, что максимальный по модулю элемент в них был бы равен единице. Для реализации этой техники надо просто поддерживать текущий максимум в каждой строке (либо поддерживать каждую строку так, чтобы максимум в ней был равен единице по модулю, но это может привести к увеличению накапливаемой погрешности).
Улучшение найденного ответа
Поскольку, несмотря на различные эвристики, алгоритм Гаусса-Жордана всё равно может приводить к большим погрешностям на специальных матрицах даже размеров порядка 
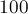
В связи с этим, полученный алгоритмом Гаусса-Жордана ответ можно улучшить, применив к нему какой-либо простой численный метод — например, метод простой итерации.
Таким образом, решение превращается в двухшаговое: сначала выполняется алгоритм Гаусса-Жордана, затем — какой-либо численный метод, принимающий в качестве начальных данных решение, полученное на первом шаге.
Такой приём позволяет несколько расширить множество задач, решаемых алгоритмом Гаусса-Жордана с приемлемой погрешностью.
Видео:Метод Гаусса решения систем линейных уравненийСкачать

Метод Гаусса на Java
Статья посвящена реализации алгоритма Гаусса для решения системы линейных алгебраических уравнений на языке Java.
Видео:12. Решение систем линейных уравнений методом ГауссаСкачать

Теоретические сведения
Рассмотрим математическую теорию. Система линейных уравнений может иметь одно решение, бесконечно много решений или же быть несовместной (не иметь решений). Не все методы решения СЛАУ могут справится с вторым случаем, когда система имеет бесконечно много решений. Например, метод Крамера и матричный метод не применимы, но метод Гаусса вполне можно использовать.
Алгоритм можно условно разделить на два этапа:
- Прямой ход
- Обратный ход
В первом этапе образуются нули ниже или выше главной диагонали, за счет использования элементарных преобразований матрицы. На втором этапе находят неизвестные начиная с конца. Подробную теорию можно посмотреть по ссылке: метод Гаусса, поэтому с теорией пожалуй все. Перейдем к реализации.
Видео:Система линейных уравнений. Общее решение. Метод ГауссаСкачать

Реализация
Начнем с постановки задачи:
- нам нужно создать программу, реализующую систему линейных уравнений в виде некоторой структуры данных, используя приемы обобщенного программирования. Система должна содержать коэффициенты производного типа от класса Number (т.е. Float, Integer, Double и т.д.)
- Запрограммировать алгоритм, который получив на вход структуру данных системы образует нули ниже главной диагонали
Начнем с написания интерфейса, который должно реализовывать каждое уравнение:
Здесь все должно быть ясно, N некоторый наследник Number‘а, T — некоторый тип, реализующий данный интерфейс (рекурсивные дженерики). Метод addEquation(T item) позволяет прибавить каждый элемент уравнения item к каждому своему элементу. Остальные методы работают аналогично.
Теперь рассмотрим класс системы уравнений. Как видно в листинге ниже, он дженеризирован так же, как и интерфейс Gauss и содержит методы для удобного доступа к приватному списку содержащих в себе уравнений.
Теперь можно приступать к реализации «частного случая» структуры уравнения. Создадим класс MyEquation, реализующий наш интерфейс. Пусть наследником Number‘а будет сверхточный класс Float (на практике лучше брать Double). Обратите внимание, что в методе addEquation(MyEquation item) используется объект класса ListIterator, позволяющий изменять элементы перебираемого списка.
Теперь имеем полноценную структуру данных, реализующую систему уравнений. Составим алгоритм который будет принимать некоторый объект, реализующий интерфейс Gauss, затем вызывая нужные методы приведет матрицу к нужному виду.
Алгоритм простой, найти нужный коэффициент, домножить на него i-ю строку (i=0..n-1), и прибавить ее к j-й строке (j=i..n). Заметьте, алгоритм не знает как именно реализуются методы findCoefficient, mul и addEquation, это придает коду бОльшую гибкость, т.к. при потребности изменить способы манипуляции уравнениями (строками), будут изменены только реализации трех вышеупомянутых методов, а главный алгоритм останется нетронутым.
Почти все. Осталось запустить это все в методе main:
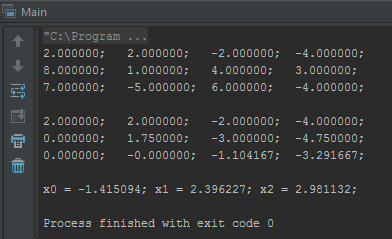
Запустим это чудо, что бы проверить корректность работы…
Это все. Исходники можно скачать на github’е.
Видео:Решение системы линейных уравнений методом Гаусса в ExcelСкачать

Вывод
Метод Гаусса не очень поддается обобщенному программированию (как видите обратный ход выполнен отдельно), однако вышла своеобразная реализация которая, надеюсь, поможет кому то лучше разобраться в искусстве использования интерфейсов и дженериков.
Видео:метод Гаусса СИСТЕМА ЛИНЕЙНЫХ УРАВНЕНИЙ решение СЛАУСкачать

Параллельное решение систем линейных уравнений.
Цель лабораторной работы
Целью данной лабораторной работы является разработка параллельной программы, которая выполняет решение системы линейных уравнений методом Гаусса. Выполнение лабораторной работы включает:
- Определение задачи решения системы линейных уравнений
- Изучение последовательного алгоритма Гаусса решения систем линейных уравнений
- Разработка параллельного алгоритма Гаусса
- Анализ эффективности параллельных вычислений в отдельности для прямого и обратного этапов метода Гаусса
- Реализация параллельного алгоритма Гаусса решения систем линейных уравнений
Введение
Системы линейных уравнений возникают при решении многих прикладных задач. Матрицы коэффициентов систем линейных уравнений могут иметь различные структуру и свойства. Мы будем полагать, что решаемая система имеет плотную матрицу высокого порядка. Линейная система n уравнений с n неизвестными x0, x1, …, xn-1 может быть представлена в виде:
В более кратком (матричном) виде система имеет вид
где A=a(i,j) есть вещественная матрица размера n×n , а вектора b и x состоят из n элементов.
Под задачей решения системы линейных уравнений для заданных матрицы А и вектора b обычно понимается нахождение значения вектора неизвестных x , при котором выполняются все уравнения системы. Метод Гаусса является широко известным прямым алгоритмом решения систем линейных уравнений, для которых матрицы коэффициентов являются плотными . Если система линейных уравнений является невырожденной , то метод Гаусса гарантирует нахождение решения с погрешностью, определяемой точностью машинных вычислений. Основная идея метода состоит в приведении матрицы А посредством эквивалентных преобразований (не меняющих решение системы) к треугольному виду, после чего значения искомых неизвестных может быть получено непосредственно в явном виде.
Изучение последовательного алгоритма Гаусса решения систем линейных уравнений
Метод Гаусса основывается на возможности выполнения преобразований линейных уравнений, которые не меняют при этом решение рассматриваемой системы (такие преобразования носят наименование эквивалентных). К числу таких преобразований относятся:
- Умножение любого из уравнений на ненулевую константу
- Перестановка уравнений
- Прибавление к уравнению любого другого уравнения системы
Метод Гаусса включает последовательное выполнение двух этапов. На первом этапе – прямой ход метода Гаусса – исходная система линейных уравнений при помощи последовательного исключения неизвестных приводится к верхнему треугольному виду
где матрица коэффициентов получаемой системы имеет вид
На обратном ходе метода Гаусса (второй этап алгоритма) осуществляется определение значений неизвестных. Из последнего уравнения преобразованной системы может быть вычислено значение переменной xn-1, после этого из предпоследнего уравнения становится возможным определение переменной xn-2 и т.д.
Прямой ход метода Гаусса
Прямой ход метода Гаусса состоит в последовательном исключении неизвестных в уравнениях решаемой системы линейных уравнений. На итерации i метода производится исключение неизвестной i для всех уравнений с номерами k , большими i . Для этого из этих уравнений осуществляется вычитание строки i , умноженной на константу (aki/aii) , с тем, чтобы результирующий коэффициент при неизвестной xi в строках оказался нулевым. Вычисления, выполняемые над элементами матрицы A и вектора b , определяются следующими соотношениями.
На рисунке представлена общая схема состояния данных на i -ой итерации прямого хода алгоритма Гаусса. Все коэффициенты при неизвестных, расположенные ниже главной диагонали и левее столбца i , уже являются нулевыми. На i -ой итерации прямого хода метода Гаусса осуществляется обнуление коэффициентов столбца i , расположенных ниже главной диагонали, путем вычитания строки i , умноженной на нужную ненулевую константу. После проведения (n-1) подобной итерации матрица, определяющая систему линейных уравнений, становится приведенной к верхнему треугольному виду.
При выполнении прямого хода метода Гаусса строка, которая используется для исключения неизвестных, носит наименование ведущей , а диагональный элемент ведущей строки называется ведущим элементом . Как можно заметить, выполнение вычислений является возможным только, если ведущий элемент имеет ненулевое значение. Более того, если ведущий элемент a(i,i) имеет малое значение, то деление и умножение строк на этот элемент может приводить к накоплению вычислительной погрешности и вычислительной неустойчивости алгоритма. Возможный способ избежать подобной проблемы может состоять в следующем – при выполнении каждой очередной итерации прямого хода метода Гаусса следует определить коэффициент с максимальным значением по абсолютной величине в столбце, соответствующем исключаемой неизвестной, т.е.
и выбрать в качестве ведущей строку, в которой этот коэффициент располагается (данная схема выбора ведущего значения носит наименование метода главных элементов).
Обратный ход алгоритма Гаусса
После приведения матрицы коэффициентов к верхнему треугольному виду становится возможным определение значений неизвестных. Из последнего уравнения преобразованной системы может быть вычислено значение переменной xn-1 , после этого из предпоследнего уравнения становится возможным определение переменной xn-2 и т.д. В общем виде, выполняемые вычисления при обратном ходе метода Гаусса могут быть представлены при помощи соотношений:
Определим вычислительную сложность метода Гаусса. В прямом ходе алгоритма для выбора ведущей строки на каждой итерации должно быть определено максимальное значение в столбце с исключаемой неизвестной. По мере исключения неизвестных количество строк и элементов в строках сокращается. Текущее число элементов строки (включая правую часть), с которыми производятся действия сложения и вычитания (первый элемент без вычислений полагается равным нулю), равно (n-i) , где i , – номер итерации прямого хода. Поскольку кроме выполнения двух операций (умножения и вычитания) с каждым элементом строки предварительно должен быть вычислен масштабирующий коэффициент aik/aii , общие затраты на выполнение действий в одной строке составят 2(n-i)+1 операций. С учетом того, что на каждой итерации обрабатывается n-i строк, общее число операций в прямом ходе метода Гаусса определяется выражением
Для реализации обратного хода на каждой i -й итерации,(итерация для удобства присваиваем номера от n-2 до 0 ) необходимо произвести n-i-1 умножений, столько же вычитаний, а также одно деление для определения очередной неизвестной. Следовательно, общая вычислительная сложность обратного хода составит
Суммируя затраты на реализацию прямого и обратного хода, получаем
В последнем равенстве пределы и порядок суммирования изменены с учетом замены j=n-i . Используя формулы суммирования,
получаем следующее соотношение для оценки вычислительной сложности метода Гаусса при его реализации в виде последовательного алгоритма:
Вычислительная сложность алгоритма Гаусса имеет порядок O(n3).
Построение параллельного алгоритма решения методом Гаусса
Поскольку решение методом Гаусса сводится к последовательности однотипных вычислительных операций умножения и сложения над строками матрицы, в качестве подзадач можно принять вычисления, связанные с обработкой одной или нескольких строк матрицы A и соответствующего элемента вектора b . Каждая итерация, связанная с решением очередной подзадачи, начинается с выбора ведущей строки. Ищется строка с наибольшим по абсолютной величине значением среди элементов i -го столбца, соответствующего исключаемой переменной xi . Поскольку строки матрицы A закреплены за разными подзадачами, для поиска максимального значения в столбце подзадачи с номерами k , должны обменяться элементами при исключаемой переменной xi . После сбора всех указанных коэффициентов может быть определено, какая из подзадач содержит ведущую строку и какое значение является ведущим элементом. Для продолжения вычислений ведущая подзадача должна разослать свою строку матрицы A и соответствующий элемент вектора b всем остальным подзадачам с номерами k, k xi . В обратном ходе метода Гаусса, как только какая-либо, например i –я подзадача, определила свою переменную xi , это значение рассылается всем подзадачам с номерами k . В каждой подзадаче полученное значение неизвестной умножается на соответствующий коэффициент и выполняется корректировка соответствующего элемента вектора b .
Масштабирование и распределение подзадач по процессорам
В качестве подзадач могут быть взяты строки матрицы A, каждая из которых при этом закрепляется за одним процессором. Если число строк матрицы больше, чем число доступных процессоров (s , подзадачи можно укрупнить, объединив несколько строк матрицы.
Анализ эффективности параллельных вычислений метода Гаусса
Пусть n – порядок системы линейных уравнений, а s, s – число используемых процессоров, т.е. матрица А имеет размер n×n , а n/s – размер полосы на каждом процессоре (для простоты полагаем, что n/s – целое число). Определим сложность параллельного варианта метода Гаусса. В прямом ходе алгоритма для выбора ведущей строки на каждой итерации и каждом процессоре должно быть определено максимальное значение в столбце с исключаемой неизвестной в пределах закрепленной за ним полосы. По мере исключения неизвестных количество строк в полосах сокращается. После сбора полученных максимальных значений, определения и рассылки ведущей строки на каждом процессоре выполняется вычитание ведущей строки из каждой строки оставшейся части строк своей полосы матрицы A . Как мы установили выше, общие затраты на выполнение действий в одной строке на i -й итерации, составляет 2(n-i)+1 операций. Если применена циклическая схема распределения данных между процессорами, то на i -й итерации каждый процессор будет обрабатывать примерно (n-i)/s строк. С учетом сказанного, общее число операций параллельного варианта прямого хода метода Гаусса определяется выражением
Заметим, что (n-i)/s , как правило, не будет целым. Для построения приближенных достаточных оценок не будем учитывать операцию округления, но на каждой итерации введем операции с одной дополнительной строкой:
На каждой i -й итерации обратного хода после рассылки очередной вычисленной неизвестной на каждом процессоре обновляются значения правых частей для (n-i)/s еще не обработанных строк из числа закрепленных за ним n / s строк. Поскольку для каждой правой части выполняются 2 операции (умножение и вычитание), общее число операций, необходимых для обновления всех правых частей, составит
Кроме обновления правых частей на каждой итерации обратного хода один из процессоров выполняет операцию деления для определения очередной переменной. При этом остальные процессоры, конечно, простаивают, но эти n операций (по числу определяемых переменных) необходимо включить в общие вычислительные затраты:
Наконец, для построения приближенных достаточных оценок, как и ранее, отменим операцию округления и добавим 2(n-1) операций, которые могут дополнительно иметь место на всех 2(n-1) итерациях обновления правых частей, если в результате округления на каждой добавляется одна строка. Тогда оценка сверху общих вычислительных затрат для реализации обратного хода составит
Таким образом суммарные затраты на реализацию прямого и обратного хода составят
Как и ранее осуществим замену j=n-i , при этом пределы суммирования при записи слагаемых в обратном порядке будут j=2..n . Тогда
Применяя те же, что и ранее, элементарные формулы для подсчета сумм, получаем
Если это допустимо, при больших n можно применять приближенную оценку:
Учтем теперь затраты на передачу данных. В прямом ходе на каждой итерации для определения ведущей строки процессоры обмениваются найденными в своей полосе максимальными значениями в столбце с исключаемой переменной. Для выполнения этой операции необходимо log2(s) шагов. С учетом количества итераций общие затраты на передачу максимальных значений
где α – латентность сети передачи данных, β – пропускная способность сети, и ω – размер пересылаемого элемента данных. На каждой итерации прямого хода метода Гаусса выполняется также рассылка выбранной ведущей строки. Сложность данной операции передачи данных определяется величиной
Наконец, при выполнении обратного хода алгоритма Гаусса на каждой итерации осуществляется рассылка всем процессорам значения очередной вычисленной неизвестной. Общее время, затрачиваемое на рассылку:
Таким образом общая сложность параллельного алгоритма Гаусса составляет
где τ – время выполнения одной вычислительной операции. С использованием приближенных оценок вычислительной сложности последовательного и параллельного алгоритмов можно построить также оценки ускорения и эффективности:
Нетрудно заметить, что при достаточно большом n и отсутствии потерь на коммуникации могут достигаться значения ускорения и эффективности близкие к предельно возможным: s и 1 соответственно. При малых n характеристики быстро падают. Например, непосредственным подсчетом легко установить, что при n =5 и s =10 ускорение составит около 5,8.
Заключение
В данной лабораторной работе была реализована параллельная программа, которая выполняет решение системы линейных уравнений методом Гаусса. Метод Гаусса является широко известным прямым алгоритмом решения систем линейных уравнений. Если система линейных уравнений является невырожденной, то метод Гаусса гарантирует нахождение решения. В данной курсовой работе также были приведены оценки трудоемкости метода Гаусса в его последовательном и параллельном варианте, а также оценки ускорения и эффективности. На основе полученных результатов можно сделать вывод, что при достаточно большом n и отсутствии потерь на коммуникации могут достигаться значения ускорения и эффективности близкие к предельно возможным: s и 1, при малых же n характеристики быстро падают.
📸 Видео
12. Метод Гаусса решения систем линейных уравнений. Часть 1.Скачать

Метод ГауссаСкачать

Алгоритм и программа решеня системы линейных уравнений методом ГауссаСкачать

МЕТОД ГАУССА 😉 #егэ #математика #профильныйегэ #shorts #огэСкачать

СЛУ Метод Гаусса в ExcelСкачать

Гаусс. Решение совместной системы линейных уравнений методом Гаусса | Домашняя работа # 1Скачать

Как решить систему уравнений методом Гаусса? Просто с лидеромСкачать

Лекция №3. преподаватель математики Сивкова Е.А.Скачать

Метод Гаусса решения систем линейных уравненийСкачать

Решение систем линейных уравнений методом Гаусса.Скачать

Общее, частное, базисное решение системы линейных уравнений Метод ГауссаСкачать




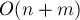 при использовании эвристики «partial pivoting» (поиск максимума в столбце)
при использовании эвристики «partial pivoting» (поиск максимума в столбце)