Решение линейных уравнений метод треугольника

Эта страничка поможет решить Системы Линейных Алгебраических Уравнений (СЛАУ) методом Гаусса, матричным методом или методом Крамера, исследовать их на совместность (теорема Кронекера-Капелли), определить количество решений, найти общее, частное и базисные решения.

Введите коэффициенты при неизвестных в поля. Если Ваше уравнение имеет меньшее количество неизвестных, то оставьте пустыми поля при переменных, не входящих в ваше уравнение. Можно использовать дроби ( 13/31 ).

Видео:Математика без Ху!ни. Вычисление определителя методом треугольников.Скачать

Определитель матрицы: алгоритм и примеры вычисления определителя матрицы

Определитель (детерминант) матрицы — некоторое число, с которым можно сопоставить любую квадратную матрицу А = ( a i j ) n × n .

|А|, ∆ , det A — символы, которыми обозначают определитель матрицы.

Способ вычисления определителя выбирают в зависимости от порядка матрицы.

Определитель матрицы 2-го порядка вычисляют по формуле:

d e t A = 1 — 2 3 1 = 1 × 1 — 3 × ( — 2 ) = 1 + 6 = 7

Видео:Определитель матрицы 3 порядка. Как легко найти? Метод треугольников и Саррюса. Просто и наглядноСкачать

Определитель матрицы 3-го порядка: правило треугольника

Чтобы найти определитель матрицы 3-го порядка, необходимо одно из правил:

• правило треугольника;
• правило Саррюса.

Как найти определитель матрицы 3-го порядка по методу треугольника?

а 11 а 12 а 13 а 21 а 22 а 23 а 31 а 32 а 33 = a 11 × a 22 × a 33 + a 31 × a 12 × a 23 + a 21 × a 32 × a 13 — a 31 × a 22 × a 13 — a 21 × a 12 × a 33 — a 11 × a 23 × a 32

А = 1 3 4 0 2 1 1 5 — 1

d e t A = 1 3 4 0 2 1 1 5 — 1 = 1 × 2 × ( — 2 ) + 1 × 3 × 1 + 4 × 0 × 5 — 1 × 2 × 4 — 0 × 3 × ( — 1 ) — 5 × 1 × 1 = ( — 2 ) + 3 + 0 — 8 — 0 — 5 = — 12

Видео:Метод Крамера за 3 минуты. Решение системы линейных уравнений - bezbotvyСкачать

Правило Саррюса

Чтобы вычислить определитель по методу Саррюса, необходимо учесть некоторые условия и выполнить следующие действия:

• дописать слева от определителя два первых столбца;
• перемножить элементы, которые расположены на главной диагонали и параллельных ей диагоналях, взяв произведения со знаком «+»;
• перемножить элементы, которые расположены на побочных диагоналях и параллельных им, взяв произведения со знаком «—».

а 11 а 12 а 13 а 21 а 22 а 23 а 31 а 32 а 33 = a 11 × a 22 × a 33 + a 31 × a 12 × a 23 + a 21 × a 32 × a 13 — a 31 × a 22 × a 13 — a 21 × a 12 × a 33 — a 11 × a 23 × a 32

А = 1 3 4 0 2 1 — 2 5 — 1 1 3 0 2 — 2 5 = 1 × 2 × ( — 1 ) + 3 × 1 × ( — 2 ) + 4 × 0 × 5 — 4 × 2 × ( — 2 ) — 1 × 1 × 5 — 3 × 0 × ( — 1 ) = — 2 — 6 + 0 + 16 — 5 — 0 = 3

Видео:Решение системы уравнений методом ГауссаСкачать

Методы разложения по элементам строки и столбца

Чтобы вычислить определитель матрицу 4-го порядка, можно воспользоваться одним из 2-х способов:

• разложением по элементам строки;
• разложением по элементам столбца.

Представленные способы определяют вычисление определителя n как вычисление определителя порядка n-1 за счет представления определителя суммой произведений элементов строки (столбца) на их алгебраические дополнения.

Разложение матрицы по элементам строки:

d e t A = a i 1 × A i 1 + a i 2 × A i 2 + . . . + а i n × А i n

Разложение матрицы по элементам столбца:

d e t A = а 1 i × А 1 i + а 2 i × А 2 i + . . . + а n i × А n i

Если раскладывать матрицу по элементам строки (столбца), необходимо выбирать строку (столбец), в которой(-ом) есть нули.

А = 0 1 — 1 3 2 1 0 0 — 2 4 5 1 3 2 1 0

• раскладываем по 2-ой строке:

А = 0 1 — 1 3 2 1 0 0 — 2 4 5 1 3 2 1 0 = 2 × ( — 1 ) 3 × 1 — 1 3 — 2 5 1 3 1 0 = — 2 × 1 — 1 3 4 5 1 2 1 0 + 1 × 0 — 1 3 — 2 5 1 3 1 0

• раскладываем по 4-му столбцу:

А = 0 1 — 1 3 2 1 0 0 — 2 4 5 1 3 2 1 0 = 3 × ( — 1 ) 5 × 2 1 0 — 2 4 5 3 2 1 + 1 × ( — 1 ) 7 × 0 1 — 1 2 1 0 3 2 1 = — 3 × 2 1 0 — 2 4 5 3 2 1 — 1 × 0 1 — 1 2 1 0 3 2 1

Видео:Вычислить определитель 3 порядка. Правило треугольникаСкачать

Свойства определителя

• если преобразовывать столбцы или строки незначительными действиями, то это не влияет на значение определителя;
• если поменять местами строки и столбцы, то знак поменяется на противоположный;
• определитель треугольной матрицы представляет собой произведение элементов, которые расположены на главной диагонали.

Пример 6

А = 1 3 4 0 2 1 0 0 5

d e t А = 1 3 4 0 2 1 0 0 5 = 1 × 5 × 2 = 10

Определитель матрицы, который содержит нулевой столбец, равняется нулю.

Видео:Решение системы уравнений методом Крамера.Скачать

Метод Гаусса онлайн

Данный онлайн калькулятор находит решение системы линейных уравнений (СЛУ) методом Гаусса. Дается подробное решение. Для вычисления выбирайте количество переменных и количество уравнений. Затем введите данные в ячейки и нажимайте на кнопку «Вычислить.»

Предупреждение

Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.

Видео:Математика без Ху!ни. Метод Гаусса.Скачать

Метод Гаусса

Метод Гаусса − это метод перехода от исходной системы линейных уравнений (при помощи эквивалентных преобразований) к системе, которая решается проще, чем исходная система.

Эквивалентными преобразованиями системы линейных уравнений являются:

• перемена местами двух уравнений в системе,
• умножение какого-либо уравнения в системе на ненулевое действительное число,
• прибавление к одному уравнению другого уравнения, умноженного на произвольное число.

Рассмотрим систему линейных уравнений:

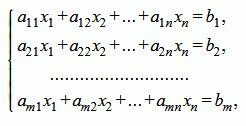(1)

Запишем систему (1) в матричном виде:

(3)

A-называется матрица коэффициентов системы, b − правая часть ограничений, x− вектор переменных, которую нужно найти. Пусть rang(A)=p.

Эквивалентные преобразования не меняют ранг матрицы коэффициентов и ранг расширеннной матрицы системы. Не меняется также множество решений системы при эквивалентных преобразованиях. Суть метода Гаусса заключается в приведении матрцы коэффициентов A к диагональному или ступенчатому.

Построим расшренную матрицу системы:

(4)

Предположим a₁₁≠0. Если это не так, то можно поменять местами эту строку со строкой с ненулевым элементом в столбце 1 (если нет таких строк, то переходим к следующему столбцу). Обнуляем все элементы столбца 1 ниже ведущего элемента a₁₁. Для этого сложим строки 2,3, . m со строкой 1, умноженной на −a₂₁/a₁₁, −a₃₁/a₁₁, . −a_m1/a₁₁, соответственно. Тогда (4) примет следующий вид:

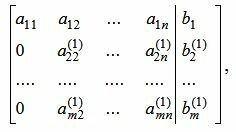(5)

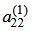
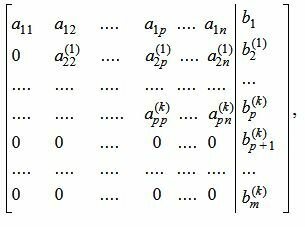На следующем этапе обнуляем все элементы столбца 2, ниже элемента . Если данный элемент нулевой, то эту строку меняем местами со строкой, лежащий ниже данной строки и имеющий ненулевой элемент во втором столбце. Далее обнуляем все элементы столбца 2 ниже ведущего элемента a₂₂. Для этого сложим строки 3, . m со строкой 2, умноженной на −a₃₂/a₂₂, . −a_m2/a₂₂, соответственно. Продолжая процедуру, получим матрицу диагонального или ступенчатого вида. Пусть полученная расширенная матрица имеет вид:

(6)

Обратим внимание на последние строки. Если 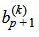. равны нулю, то система линейных уравнений имеет решение, если же хотя бы один из этих чисел отлично от нуля, то система несовместна. Иными словами, система (2) совместна тогда и только тогда, когда ранг матрицы A навен рангу расширенной матрицы (A|b).

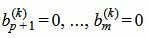
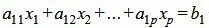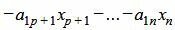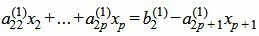Пусть . Тогда

(7)

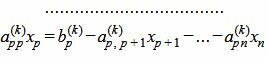Так как rangA=rang(A|b), то множество решений (7) есть (n−p)− многообразие. Следовательно n−p неизвестных можно выбрать произвольно. Остальные неизвестные из системы (7) вычисляются так. Из последнего уравнения выражаем x_p через остальные переменные и вставляем в предыдущие выражения. Далее из предпоследнего уравнения выражаем x_p−1 через остальные переменные и вставляем в предыдущие выражения и т.д. Рассмотрим метод Гаусса на конкретных примерах.

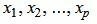
Видео:Решение системы трех уравнений по формулам КрамераСкачать

Примеры решения системы линейных уравнений методом Гаусса

Пример 1. Найти общее решение системы линейных уравнений методом Гаусса:

Матричный вид записи: Ax=b, где

Для решения системы, запишем расширенную матрицу:

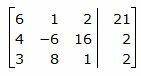Обозначим через a_ij элементы i-ой строки и j-ого столбца.

Исключим элементы 1-го столбца матрицы ниже элемента a_{1 1}. Для этого сложим строки 2,3 со строкой 1, умноженной на -2/3,-1/2 соответственно:

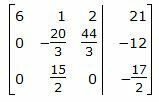Исключим элементы 2-го столбца матрицы ниже элемента a2 2. Для этого сложим строку 3 со строкой 2, умноженной на 9/8:

Делим каждую строку матрицы на соответствующий ведущий элемент (если ведущий элемент существует):

Из вышеизложенной таблицы можно записать:

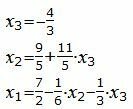Подставив верхние выражения в нижние, получим решение.

,,.

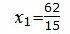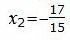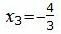Пример 2. Найти общее решение системы линейных уравнений методом Гаусса:

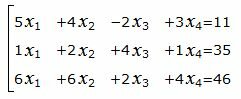Матричный вид записи: Ax=b, где

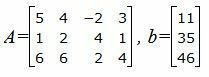Для решения системы, построим расширенную матрицу:

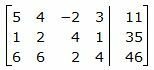Обозначим через a_ij элементы i-ой строки и j-ого столбца.

Исключим элементы 1-го столбца матрицы ниже элемента a₁₁. Для этого сложим строки 2,3 со строкой 1, умноженной на -1/5,-6/5 соответственно:

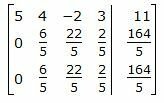Исключим элементы 2-го столбца матрицы ниже элемента a₂₂. Для этого сложим строку 3 со строкой 2, умноженной на -1:

Делим каждую строку матрицы на соответствующий ведущий элемент (если ведущий элемент существует):

Выразим переменные x₁, x₂ относительно остальных переменных.

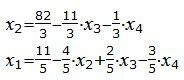где x₃, x₄− произвольные действительные числа.

Подставив верхние выражения в нижние, получим решение.

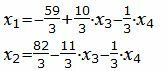где x₃, x₄− произвольные действительные числа.

Векторный вариант решения:

Запишем вышеизложенное решение, представив свободные переменные в виде тождеств:

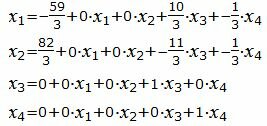Тогда векторное решение можно представить так:

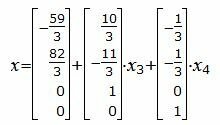где x₃, x₄− произвольные действительные числа.

🎬 Видео

Урок 1. Матрицы, определитель матрицы и ранг матрицы | Высшая математика | TutorOnlineСкачать

Решение системы уравнений методом Крамера 2x2Скачать

Математика Без Ху!ни. Система линейных уравнений. Метод Крамера.Скачать

5 способов вычисления определителя ★ Какой способ лучше?Скачать

ЛИНЕЙНЫЕ УРАВНЕНИЯ - Как решать линейные уравнения // Подготовка к ЕГЭ по МатематикеСкачать

Решение систем линейных алгебраических уравнений методом Крамера.Скачать

Математика без Ху!ни. Метод Гаусса. Совместность системы. Ранг матрицы.Скачать

§10 Правило треугольникаСкачать

Решение системы линейных уравнений методом ГауссаСкачать

6. Вычисление определителя 2 и 3 порядка.Скачать

Решение системы уравнений методом Гаусса 4x4Скачать

Определители матриц 2 и 3 порядка (правило треугольника, Саррюса, разложение по строке)Скачать