В данной статье рассмотрим принцип решения таких уравнений как линейные уравнения. Запишем определение этих уравнений, зададим общий вид. Разберем все условия нахождения решений линейных уравнений, используя, в том числе, практические примеры.
Обратим внимание, что материал ниже содержит информацию по линейным уравнениям с одной переменной. Линейные уравнения с двумя переменными рассматриваются в отдельной статье.
- Что такое линейное уравнение
- Принцип решения линейных уравнений
- Примеры решения линейных уравнений
- Решение простых линейных уравнений
- Понятие уравнения
- Какие бывают виды уравнений
- Как решать простые уравнения
- Примеры линейных уравнений
- Методика введения решения линейных уравнений и уравнений, сводящихся к линейным
- 📺 Видео
Видео:Алгебра 7 класс (Урок№43 - Решение линейных уравнений с одним неизвестным.)Скачать

Что такое линейное уравнение
Линейное уравнение – это уравнение, запись которого такова:
a · x = b , где x – переменная, a и b – некоторые числа.
Такая формулировка использована в учебнике алгебры ( 7 класс) Ю.Н.Макарычева.
Примерами линейных уравнений будут:
3 · x = 11 (уравнение с одной переменной x при а = 5 и b = 10 );
− 3 , 1 · y = 0 (линейное уравнение с переменной y, где а = — 3 , 1 и b = 0 );
x = − 4 и − x = 5 , 37 (линейные уравнения, где число a записано в явном виде и равно 1 и — 1 соответственно. Для первого уравнения b = — 4 ; для второго — b = 5 , 37 ) и т.п.
В различных учебных материалах могут встречаться разные определения. К примеру, Виленкин Н.Я. к линейным относит также те уравнения, которые возможно преобразовать в вид a · x = b при помощи переноса слагаемых из одной части в другую со сменой знака и приведения подобных слагаемых. Если следовать такой трактовке, уравнение 5 · x = 2 · x + 6 – также линейное.
А вот учебник алгебры ( 7 класс) Мордковича А.Г. задает такое описание:
Линейное уравнение с одной переменной x – это уравнение вида a · x + b = 0 , где a и b – некоторые числа, называемые коэффициентами линейного уравнения.
Примером линейных уравнений подобного вида могут быть:
3 · x − 7 = 0 ( a = 3 , b = − 7 ) ;
1 , 8 · y + 7 , 9 = 0 ( a = 1 , 8 , b = 7 , 9 ) .
Но также там приведены примеры линейных уравнений, которые мы уже использовали выше: вида a · x = b , например, 6 · x = 35 .
Мы сразу условимся, что в данной статье под линейным уравнением с одной переменной мы будем понимать уравнение записи a · x + b = 0 , где x – переменная; a , b – коэффициенты. Подобная форма линейного уравнения нам видится наиболее оправданной, поскольку линейные уравнения – это алгебраические уравнения первой степени. А прочие уравнения, указанные выше, и уравнения, приведенные равносильными преобразованиями в вид a · x + b = 0 , определим, как уравнения, сводящиеся к линейным уравнениям.
При таком подходе уравнение 5 · x + 8 = 0 – линейное, а 5 · x = − 8 — уравнение, сводящееся к линейному.
Видео:ЛИНЕЙНЫЕ УРАВНЕНИЯ - Как решать линейные уравнения // Подготовка к ЕГЭ по МатематикеСкачать

Принцип решения линейных уравнений
Рассмотрим, как определить, будет ли заданное линейное уравнение иметь корни и, если да, то сколько и как их определить.
Факт наличия корней линейного уравнения определятся значениями коэффициентов a и b . Запишем эти условия:
- при a ≠ 0 линейное уравнение имеет единственный корень x = — b a ;
- при a = 0 и b ≠ 0 линейное уравнение не имеет корней;
- при a = 0 и b = 0 линейное уравнение имеет бесконечно много корней. По сути в данном случае любое число может стать корнем линейного уравнения.
Дадим пояснение. Нам известно, что в процессе решения уравнения возможно осуществлять преобразование заданного уравнения в равносильное ему, а значит имеющее те же корни, что исходное уравнение, или также не имеющее корней. Мы можем производить следующие равносильные преобразования:
- перенести слагаемое из одной части в другую, сменив знак на противоположный;
- умножить или разделить обе части уравнения на одно и то же число, не равное нулю.
Таким образом, преобразуем линейное уравнение a · x + b = 0 , перенеся слагаемое b из левой части в правую часть со сменой знака. Получим: a · x = − b .
Далее мы разделим обе части равенства на число а , при этом условившись, что это число отлично от нуля, иначе деление станет невозможным. Случай, когда а = 0 , рассмотрим позже.
Итак, производим деление обеих частей уравнения на не равное нулю число а, получив в итоге равенство вида x = — b a . Т.е., когда a ≠ 0 , исходное уравнение a · x + b = 0 равносильно равенству x = — b a , в котором очевиден корень — b a .
Методом от противного возможно продемонстрировать, что найденный корень – единственный. Зададим обозначение найденного корня — b a как x 1 . Выскажем предположение, что имеется еще один корень линейного уравнения с обозначением x 2 . И конечно: x 2 ≠ x 1 , а это, в свою очередь, опираясь на определение равных чисел через разность, равносильно условию x 1 − x 2 ≠ 0 . С учетом вышесказанного мы можем составить следующие равенства, подставив корни:
a · x 1 + b = 0 и a · x 2 + b = 0 .
Свойство числовых равенств дает возможность произвести почленное вычитание частей равенств:
a · x 1 + b − ( a · x 2 + b ) = 0 − 0 , отсюда: a · ( x 1 − x 2 ) + ( b − b ) = 0 и далее a · ( x 1 − x 2 ) = 0 . Равенство a · ( x 1 − x 2 ) = 0 является неверным, поскольку ранее условием было задано, что a ≠ 0 и x 1 − x 2 ≠ 0 . Полученное противоречие и служит доказательством того, что при a ≠ 0 линейное уравнение a · x + b = 0 имеет лишь один корень.
Обоснуем еще два пункта условий, содержащие a = 0 .
Когда a = 0 линейное уравнение a · x + b = 0 запишется как 0 · x + b = 0 . Свойство умножения числа на нуль дает нам право утверждать, что какое бы число не было взято в качестве x, подставив его в равенство 0 · x + b = 0 , получим b = 0 . Равенство справедливо при b = 0 ; в прочих случаях, когда b ≠ 0 , равенство становится неверным.
Таким образом, когда a = 0 и b = 0 , любое число может стать корнем линейного уравнения a · x + b = 0 , поскольку при выполнении этих условий, подставляя вместо x любое число, получаем верное числовое равенство 0 = 0 . Когда же a = 0 и b ≠ 0 линейное уравнение a · x + b = 0 вовсе не будет иметь корней, поскольку при выполнении указанных условий, подставляя вместо x любое число, получаем неверное числовое равенство b = 0 .
Все приведенные рассуждения дают нам возможность записать алгоритм, дающий возможность найти решение любого линейного уравнения:
- по виду записи определяем значения коэффициентов a и b и анализируем их;
- при a = 0 и b = 0 уравнение будет иметь бесконечно много корней, т.е. любое число станет корнем заданного уравнения;
- при a = 0 и b ≠ 0 заданное уравнение не будет иметь корней;
- при a , отличном от нуля, начинаем поиск единственного корня исходного линейного уравнения:
- перенесем коэффициент b в правую часть со сменой знака на противоположный, приводя линейное уравнение к виду a · x = − b ;
- обе части полученного равенства делим на число a , что даст нам искомый корень заданного уравнения: x = — b a .
Собственно, описанная последовательность действий и есть ответ на вопрос, как находить решение линейного уравнения.
Напоследок уточним, что уравнения вида a · x = b решаются по похожему алгоритму с единственным отличием, что число b в такой записи уже перенесено в нужную часть уравнения, и при a ≠ 0 можно сразу выполнять деление частей уравнения на число a .
Таким образом, чтобы найти решение уравнения a · x = b , используем такой алгоритм:
- при a = 0 и b = 0 уравнение будет иметь бесконечно много корней, т.е. любое число может стать его корнем;
- при a = 0 и b ≠ 0 заданное уравнение не будет иметь корней;
- при a , не равном нулю, обе части уравнения делятся на число a , что дает возможность найти единственный корень, который равен b a .
Видео:Решение уравнений, сводящихся к линейным | Алгебра 7 класс #18 | ИнфоурокСкачать

Примеры решения линейных уравнений
Необходимо решить линейное уравнение 0 · x − 0 = 0 .
Решение
По записи заданного уравнения мы видим, что a = 0 и b = − 0 (или b = 0 , что то же самое). Таким образом, заданное уравнение может иметь бесконечно много корней или любое число.
Ответ: x – любое число.
Видео:Как решать уравнения? уравнение 7 класс. Линейное уравнениеСкачать

Решение простых линейных уравнений
О чем эта статья:
Видео:Линейное уравнение с двумя переменными. 7 класс.Скачать

Понятие уравнения
Уравнение — это математическое равенство, в котором неизвестна одна или несколько величин. Значение неизвестных нужно найти так, чтобы при их подстановке в пример получилось верное числовое равенство.
Например, возьмем выражение 2 + 4 = 6. При вычислении левой части получается верное числовое равенство, то есть 6 = 6.
Уравнением можно назвать выражение 2 + x = 6, с неизвестной переменной x, значение которой нужно найти. Результат должен быть таким, чтобы знак равенства был оправдан, и левая часть равнялась правой.
Корень уравнения — то самое число, которое при подстановке на место неизвестной уравнивает выражения справа и слева.
Решить уравнение значит найти все возможные корни или убедиться, что их нет.
Решить уравнение с двумя, тремя и более переменными — это два, три и более значения переменных, которые обращают данное выражение в верное числовое равенство.
Равносильные уравнения — это те, в которых совпадают множества решений. Другими словами, у них одни и те же корни.
Видео:Урок 7 ЛИНЕЙНОЕ УРАВНЕНИЕ С ОДНОЙ ПЕРЕМЕННОЙСкачать

Какие бывают виды уравнений
Уравнения могут быть разными, самые часто встречающиеся — линейные и квадратные.
Особенность преобразований алгебраических уравнений в том, что в левой части должен остаться многочлен от неизвестных, а в правой — нуль.
Линейное уравнение выглядят так: ах + b = 0, где a и b — действительные числа. Вот, что поможет в решении:
если а ≠ 0 — уравнение имеет единственный корень: х = -b : а;
если а = 0 — уравнение корней не имеет;
если а и b равны нулю, то корнем уравнения является любое число.
Квадратное уравнение выглядит так: ax2 + bx + c = 0, где коэффициенты a, b и c — произвольные числа, a ≠ 0.
Числовой коэффициент — число, которое стоит при неизвестной переменной.
Кроме линейных и квадратных есть и другие виды уравнений, с которыми мы познакомимся в следующий раз:
Онлайн-курсы по математике за 7 класс помогут закрепить новые знания на практике с талантливым преподавателем.
Видео:Алгебра 7 Линейное уравнение с одной переменнойСкачать

Как решать простые уравнения
Чтобы научиться решать простые линейные уравнения, нужно запомнить формулу и два основных правила.
1. Правило переноса. При переносе из одной части в другую, член уравнения меняет свой знак на противоположный.
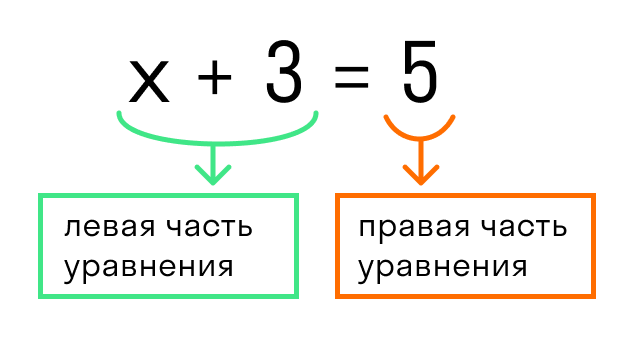
Для примера рассмотрим простейшее уравнение: x+3=5.
Начнем с того, что в каждом уравнении есть левая и правая часть.
Перенесем 3 из левой части в правую и меняем знак на противоположный.
Можно проверить: 2 + 3 = 5. Все верно. Корень равен 2.
Решим еще один пример: 6x = 5x + 10.
Перенесем 5x из правой части в левую. Знак меняем на противоположный, то есть на минус.
Приведем подобные и завершим решение.
2. Правило деления. В любом уравнении можно разделить левую и правую часть на одно и то же число. Это может ускорить процесс решения. Главное — быть внимательным, чтобы не допустить глупых ошибок.
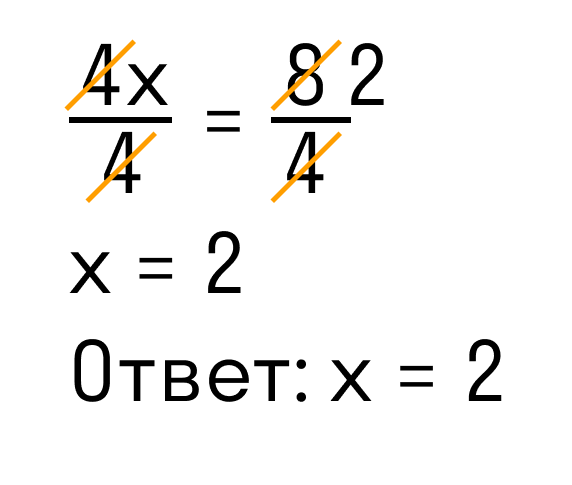
Применим правило при решении примера: 4x=8.
При неизвестной х стоит числовой коэффициент — 4. Их объединяет действие — умножение.
Чтобы решить уравнение, нужно сделать так, чтобы при неизвестной x стояла единица.
Разделим каждую часть на 4. Как это выглядит:
Теперь сократим дроби, которые у нас получились и завершим решение линейного уравнения:
Рассмотрим пример, когда неизвестная переменная стоит со знаком минус: -4x = 12
- Разделим обе части на -4, чтобы коэффициент при неизвестной стал равен единице.
-4x = 12 | : (-4)
x = −3
Если знак минус стоит перед скобками, и по ходу вычислений его убрали — важно не забыть поменять знаки внутри скобок на противоположные. Этот простой факт позволит не допустить обидные ошибки, особенно в старших классах.
Напомним, что не у каждого линейного уравнения есть решение — иногда корней просто нет. Изредка среди корней может оказаться ноль — ничего страшного, это не значит, что ход решения оказался неправильным. Ноль — такое же число, как и остальные.
Способов решения линейных уравнений немного, нужно запомнить только один алгоритм, который будет эффективен для любой задачки.
| Алгоритм решения простого линейного уравнения |
|---|
|
Чтобы быстрее запомнить ход решения и формулу линейного уравнения, скачайте или распечатайте алгоритм — храните его в телефоне, учебнике или на рабочем столе.
Видео:Линейное уравнение с одной переменной. 6 класс.Скачать

Примеры линейных уравнений
Теперь мы знаем, как решать линейные уравнения. Осталось попрактиковаться на задачках, чтобы чувствовать себя увереннее на контрольных. Давайте решать вместе!
Пример 1. Как правильно решить уравнение: 6х + 1 = 19.
ЮПеренести 1 из левой части в правую со знаком минус.
Разделить обе части на множитель, стоящий перед переменной х, то есть на 6.
Пример 2. Как решить уравнение: 5(х − 3) + 2 = 3(х − 4) + 2х − 1.
5х − 15 + 2 = 3х − 12 + 2х − 1
Сгруппировать в левой части члены с неизвестными, а в правой — свободные члены. Не забываем при переносе из одной части уравнения в другую поменять знаки на противоположные у переносимых членов.
5х − 3х − 2х = −12 − 1 + 15 − 2
Приведем подобные члены.
Ответ: х — любое число.
Пример 3. Решить: 4х = 1/8.
Разделим обе части уравнения на множитель стоящий перед переменной х, то есть на 4.
Пример 4. Решить: 4(х + 2) = 6 − 7х.
Видео:ЛИНЕЙНОЕ УРАНЕНИЕ С ДВУМЯ ПЕРЕМЕННЫМИ — Как решать линейное уравнение // Алгебра 7 классСкачать

Методика введения решения линейных уравнений и уравнений, сводящихся к линейным
Разделы: Математика
Изучение уравнений в среднем звене начинается с введения решения линейных уравнений и уравнений, сводящихся к линейным.
Равенство двух функций, рассматриваемых в общей области определения, называется уравнением. Переменные, входящие в уравнение, обозначаются латинскими буквами x, y,z, t … Уравнение с одной переменной х в общем, виде записывается так f(x)= g(x).
Всякое значение переменной, при котором выражения f(x) и g(x) принимают равные числовые значения, называется корнем уравнения.
Решить уравнение – это, значит, найти все его корни или доказать, что их нет.
Например, уравнение 3+x=7 имеет единственный корень 4, так как при этом и только при этом значении переменной 3+x=7 верное равенство.
Уравнение (x-1)(x-2)=0 имеет 2 корня 1 и 2.
Уравнение x 2 +1=0 не имеет действительных корней, так как сумма двух положительных чисел не равняется 0.
Для того, чтобы решить любое уравнение с одной переменной, учащийся должен знать: во-первых, правила, формулы или алгоритмы решения уравнений данного вида и, во-вторых, правила выполнения тождественных и равносильных преобразований, с помощью которых данное уравнение можно привести к простейшим.
Таким образом, решение каждого уравнения складывается из двух основных частей:
- преобразования данного уравнения к простейшим;
- решения простейших уравнений по известным правилам, формулам или алгоритмам.
Если вторая часть является алгоритмической, то первая часть — в значительной степени — эвристической, что и представляет наибольшую трудность для учащихся. В процессе решения уравнения его стараются заменить более простым, поэтому важно знать с помощью каких преобразований это возможно. Здесь необходимо в доступной для ребенка форме дать понятие равносильности.
Уравнения, имеющие одни и теже корни, называются равносильными. Равносильными считаются и уравнения, каждое из которых не имеет корней.
Например, уравнения x+2=5 и x+5=8 равносильны, так как каждое из них имеет единственный корень — число 3.Равносильны и уравнения x 2 +1=0 и 2x 2 +5=0 — ни одно из них не имеет корней.
Уравнения х-5=1 и х 2 =36 не равносильны, так как первое имеет только один корень х=6, тогда как второе имеет два корня 6 и –6.
К равносильным преобразованиям относятся:
1) Если к обеим частям уравнения прибавить одно и тоже число или одно и тоже целое алгебраическое выражение, содержащее неизвестное, то новое уравнение будет равносильно данному.
2) Если обе части уравнения умножить или разделить на одно и тоже отличное от нуля число, то получится уравнение, равносильное данному.
Например, уравнение 
3) Если в уравнении произвести раскрытие скобок и привести подобные слагаемые, то получится уравнения, равносильно данному.
Обучение решения уравнений начинается с простейших линейных уравнений и уравнений сводящихся к ним. Дается определение линейного уравнения и рассматриваются случаи, когда оно имеет одно решение; не имеет решений и имеет бесконечное множество решений.
Линейным уравнением с одной переменной х называют уравнение вида ах = b, где а и b — действительные числа, а — называют коэффициентом при переменной, b — свободным членом.
Для линейного уравнения ах = b могут представиться при случае:
- а
0, в этом случае корень уравнения равен b/a
- а = 0; b = 0; в этом случае уравнение принимает вид 0
х = b, что верно при любом х, т.е. корнем уравнения служит любое действительное число;
- а = 0; b
0; в том случае уравнение принимает вид 0
х = b, оно не имеет корней.
Многие уравнения в результате преобразований сводятся к линейным.
Так в 7 классе можно применить следующие уравнения:
1)
Это уравнение сводиться к линейному уравнению.
Умножением обеих частей на 12 (наименьшее общее краткое знаменателей 3, 4, 6, 12), получим:
8 + 3x + 2 – 2x = 5x –12,
8 + 2 + 12 = 5x – 3x + 2x,
2) Покажем, что уравнение 2 (х + 1) – 1 = 3 — (1 — 2х) не имеет корней.
Упростим обе части уравнения:
2х + 2 – 1 = 3 – 1 + 2х,
Это уравнение не имеет корней, т.к. левая часть 0 х равна 0 при любом х, а значит не равна 1.
3) Покажем, что уравнение 3(1 – x) + 2 = 5 – 3x имеет бесконечное множество корней.
При прохождении темы “линейные уравнения с двумя переменными” можно предложить учащимся графический способ решения уравнения. Данный метод основан на пользовании графиков функций, входящих в уравнение. Суть метода: найти абсциссы точек пересечения графиков функций, стоящих в левой и правой частях уравнения. Основывается на выполнение следующих действий:
1) Преобразовать исходное уравнение к виду f(x) = g(x), где f(x) и g(x) функции, графики, которых можно построить.
2) Построить графики функций f(x) и g(x)
3) Определить точки пересечения построенных графиков.
4) Определить абсциссы найденных точек. Они и дадут множество решений исходного уравнения.
5) Записать ответ.
Преимущество данного метода заключается в том, что он позволяет легко определить число корней уравнения. Недостаток в том, что корни в общем случае определяются приближенно.
Следующим этапом в изучении линейных уравнений, являются уравнения с модулями, причем некоторые решения выполняются несколькими способами.
Решение уравнений, содержащих знак модуля и уравнений с параметрами можно назвать деятельностью, близкой к исследовательской. Это обусловлено тем, что выбор метода решения, процесс решения, запись ответа предполагают определенный уровень сформированности умений наблюдать, сравнивать, анализировать, выдвигать и проверять гипотезу, обобщать полученные результаты.
Особой интерес представляют уравнения, содержащие знак модуля.
По определению модуля числа a, имеем:
Число –a может быть отрицательным при a>0; -a положительным при a -1, тогда

Видим, что число 0 принадлежит промежутку. Значит, является корнем. Таким образом, уравнение 
На простых примерах рассмотрим алгоритм решения уравнений с параметрами: область допустимых значений, область определения, общие решения, контрольные значения параметров, типы частных уравнений. Способы их нахождения будут устанавливаться в каждом виде уравнений отдельно.
На базе введенных понятий определим общую схему решения всякого уравнения F(a;x)=0 с параметром а (для случая двух параметров схема аналогична):
- устанавливаются область допустимых значений параметра и область определения;
- определяются контрольные значения параметра, разбивающие область допустимых значений параметра на области однотипности частных уравнений;
- для контрольных значений параметра соответствующие частные уравнения исследуются отдельно;
- находятся общие решения x=f1 (a),…, fk (a) уравнения F(a;x)=0 на соответствующих множествах Аf1,…, Аfk значений параметра;
- составляется модель общих решений, контрольных значений параметра;
- на модели выделяются промежутки значений параметра с одинаковыми общими решениями (области однотипности);
- для контрольных значений параметра и выделенных областей однотипности записываются характеристики всех типов частных уравнений
- Особое место в алгебре отводится линейным уравнениям с параметрами.
Рассмотрим несколько примеров.
| 1. | 2х – 3 = m +1, +1, |
2х – 3 = 
Умножим обе части уравнения на 3, получим
6х — m•х + 12m + 12,

 , при m
, при m  6.
6.Уравнение 2х – 3 + m (х/3 + 4) + 1 имеет множество решений, заданных формулой 
2. 



mx – n = 2x – 2 + 2n + 3xn,
mx – 2x – 3xn = — 2 + 2n +n,
mx – 2x – 3xn = 3n – 2,
x (m – 2 – 3n) = 3n – 2, при m 


Рассмотрим случай, где a = 0, тогда
m = 3n +2, при n 
n = 
m = 3 • 
x(4 – 2 – 3 

x – любое число, кроме x = 1.
б) 3n – 2 
0 • x = b. В этом случае уравнение не имеет решений.
2) a 
m – 2 – 3n 
m 
x = 


3n – 2 
3n + 3n 
6n 

В этом случае уравнение решений не имеет.
Значит, при n = 
(n 


Ответ: 1. n = 

2. n = 0, m = 6n (n 

3. n 




В дальнейшем предлагается рассмотреть решение задач методом составления линейных уравнений. Это сложный процесс, где надо уметь думать, догадываться, хорошо знать фактически материал.
В процессе решения каждой задачи надо четко размечать четыре этапа:
- изучение условия задачи;
- поиск плана решения и его составление;
- оформление найденного решения;
- критический анализ результата решения.
Теперь рассмотрим задачи, при решении которых применяются линейные уравнения.
1. Сплав меди и цинка содержит меди на 640 г. Больше, чем цинка. После того, как из сплава выделили 6/7 содержащейся в нем меди и 60% цинка, масса сплава оказалась равной 200 г. Какова была масса сплава первоначально?
Пусть в сплаве было х г. цинка, тогда меди (640 + х) г. после того, как выделили 6/7 меди и 60% цинка, осталось 1/7 меди и 40% цинка, т.е. 0,4 части. Зная, что масса сплава оказалась равной 200 г., составим уравнение.
1/7 (х + 640) + 0,4•х = 200,
х + 640 + 2,8•х =1400,
Значит, цинка было 200 г., а меди 840 г.
(200 + 640 = 840). 1) 200 + 840 = 1040 (г.) – масса сплава. Ответ: первоначальная масса сплава 1040 г.
2. Сколько литров 60% серной кислоты нужно прибавить к 10 л 30% кислоты, чтобы получить 40% раствор?
Пусть число литров 60% кислоты, которое прибавим х л, тогда раствора чистой кислоты будет 





60х + 300 = 40х + 400,
60х – 40х = 400 – 300,
Значит, нужно прибавить 5 л 60% кислоты.
При изучении темы “Решение линейных уравнений” рекомендуется некоторая историческая справка.
Задачи на решение уравнений первой степени встречаются еще в вавилонских клинописных текстах. В них же есть некоторые задачи, приводящие к квадратным и даже кубическим уравнениям (последние, по-видимому, решались с помощью подбора корней). Древнегреческие математики нашли геометрическую форму решения квадратного уравнения. В геометрической же форме арабский математик Омар Хайям (конец XI – начало XII века н. э.) исследовал кубическое уравнение, хотя и не нашел общей формулы для его решения. Решение кубического уравнения было найдено в начале XVI века в Италии. После того, как Сципиан дель Ферро решил один частный вид таких уравнений в 1535 году, итальянец Тарталья нашел общую формулу. Он доказал, что корни уравнения x 3 + px + q = 0 имеют вид x =
Это выражение обычно называют формулой Кардано, по имени ученого, узнавшего ее от Тартальи и опубликовавшего в 1545 году в своей книге “Великое искусство алгебраических правил”. Ученик Кардано – молодой математик Феррари решил общее уравнение четвертой степени. После этого на протяжении двух с половиной столетий продолжались поиски формулы для решения уравнений пятой степени. В 1823 году замечательный норвежский математик Нильс Хендрик Абель (1802-1829) доказал, что такой формулы не существует. Точнее говоря, он доказал, что корни общего уравнения пятой степени нельзя выразить через его коэффициенты с помощью арифметических действий и операций извлечения корня. Глубокое исследование вопроса об условиях разрешимости уравнений в радикалах провел французский математик Эварист Галуа (1811-1832), погибший на дуэли в возрасте 21 года. Некоторые проблемы теории Галуа решил советский алгебраист И.Т.Шафаревич.
Наряду с поисками формулы для решения уравнения пятой степени велись и другие исследования в области теории алгебраических уравнений. Виета установил связь между коэффициентами уравнений и его корнями. Он доказал, что если x1,…,xn – корни уравнения x n + a1x n-1 +…+an=0, то имеют место формулы:
Литература:
- Журнал “Математика в школе” 6, 1999
- Приложение к газете “Первое сентября”- математика 20, 1999.
- С.И. Туманов “Алгебра”, пособие для учащихся 6-8 классов.
- Н.И. Александров; И. П.Ярандай “Словарь-справочник по математике”.
- О.Б. Епишева; В.И. Крупич “Учить школьников учиться математике”.
- Е.И.Ямщенко “Изучение функций”.
- А.И. Худобин; М.Ф. Шуршалов “Сборник задач по алгебре и элементарным функциям”.
- Ш. А. Алимов, В.А. Ильин “Алгебра 6-8 классы”.
📺 Видео
Решение уравнений с одним неизвестным, сводящихся к линейным. Алгебра. 7 класс.Скачать

Алгебра 7 Линейное уравнение с двумя переменными и его графикСкачать

7 класс, 4 урок, Линейное уравнение с одной переменнойСкачать

Видеоурок. 7 класс. Решение линейных уравнений с одним неизвестнымСкачать

Решаем линейные уравнения на ОГЭ по математике 2022. Блок №1Скачать

Линейные уравненияСкачать

Алгебра 7 класс. 11 сентября. Решение линейных уравнений #1Скачать

Как решать линейные уравнения #математика #математика7классСкачать

МЕТОД ПОДСТАНОВКИ 😉 СИСТЕМЫ УРАВНЕНИЙ ЧАСТЬ I#математика #егэ #огэ #shorts #профильныйегэСкачать

Решение простых линейных уравнений. 6 класс.Скачать

Как решать линейные уравнения Решите уравнение 5 класс 6 класс 7 класс Как решать простое уравнениеСкачать


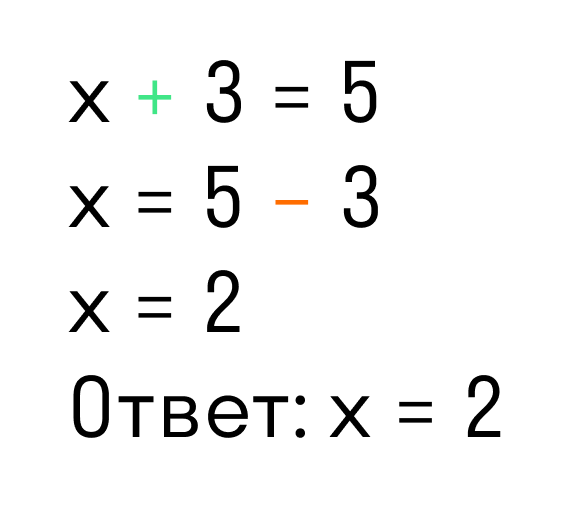



 0, в этом случае корень уравнения равен b/a
0, в этом случае корень уравнения равен b/a х = b, что верно при любом х, т.е. корнем уравнения служит любое действительное число;
х = b, что верно при любом х, т.е. корнем уравнения служит любое действительное число; 0; в том случае уравнение принимает вид 0
0; в том случае уравнение принимает вид 0 х = b, оно не имеет корней.
х = b, оно не имеет корней.

