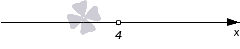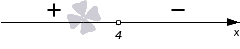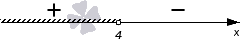Решение линейных уравнений и неравенств с одной переменной основные свойства их решений

После получения начальных сведений о неравенствах с переменными, переходим к вопросу их решения. Разберем решение линейных неравенств с одной переменной и все методы для их разрешения с алгоритмами и примерами. Будут рассмотрены только линейные уравнения с одной переменной.

Видео:Как решать неравенства? Часть 1| МатематикаСкачать

Что такое линейное неравенство?

В начале необходимо определить линейное уравнение и выяснить его стандартный вид и чем оно будет отличаться от других. Из школьного курса имеем, что у неравенств нет принципиального различия, поэтому необходимо использовать несколько определений.

Линейное неравенство с одной переменной x – это неравенство вида a · x + b > 0 , когда вместо > используется любой знак неравенства , ≤ , ≥ , а и b являются действительными числами, где a ≠ 0 .

Неравенства a · x c или a · x > c , с x являющимся переменной, а a и c некоторыми числами, называют линейными неравенствами с одной переменной.

Так как ничего не сказано за то, может ли коэффициент быть равным 0 , тогда строгое неравенство вида 0 · x > c и 0 · x c может быть записано в виде нестрогого, а именно, a · x ≤ c , a · x ≥ c . Такое уравнение считается линейным.

Их различия заключаются в:

• форме записи a · x + b > 0 в первом, и a · x > c – во втором;
• допустимости равенства нулю коэффициента a , a ≠ 0 — в первом, и a = 0 — во втором.

Считается, что неравенства a · x + b > 0 и a · x > c равносильные, потому как получены переносом слагаемого из одной части в другую. Решение неравенства 0 · x + 5 > 0 приведет к тому, что его необходимо будет решить, причем случай а = 0 не подойдет.

Считается, что линейными неравенствами в одной переменной x считаются неравенства вида a · x + b 0 , a · x + b > 0 , a · x + b ≤ 0 и a · x + b ≥ 0 , где a и b являются действительными числами. Вместо x может быть обычное число.

Исходя из правила, имеем, что 4 · x − 1 > 0 , 0 · z + 2 , 3 ≤ 0 , — 2 3 · x — 2 0 являются примерами линейных неравенств. А неравенства такого плана, как 5 · x > 7 , − 0 , 5 · y ≤ − 1 , 2 называют сводящимися к линейному.

Видео:Линейное уравнение с одной переменной. 6 класс.Скачать

Как решить линейное неравенство

Основным способом решения таких неравенств сводится к равносильным преобразованиям для того, чтобы найти элементарные неравенства x p ( ≤ , > , ≥ ) , p являющееся некоторым числом, при a ≠ 0 , а вида a p ( ≤ , > , ≥ ) при а = 0 .

Для решения неравенства с одной переменной, можно применять метода интервалов или изображать графически. Любой из них можно применять обособленно.

Видео:Как понять неравенства? Квадратные неравенства. Линейные и сложные неравенства | TutorOnlineСкачать

Используя равносильные преобразования

Чтобы решить линейное неравенство вида a · x + b 0 ( ≤ , > , ≥ ) , необходимо применить равносильные преобразования неравенства. Коэффициент может быть равен или не равен нулю. Рассмотрим оба случая. Для выяснения необходимо придерживаться схемы, состоящей из 3 пунктов: суть процесса, алгоритм, само решение.

Алгоритм решение линейного неравенства a · x + b 0 ( ≤ , > , ≥ ) при a ≠ 0

• число b будет перенесено в правую часть неравенства с противоположным знаком, что позволит прийти к равносильному a · x − b ( ≤ , > , ≥ ) ;
• будет производиться деление обеих частей неравенства на число не равное 0 . Причем , когда a является положительным, то знак остается, когда a – отрицательное, меняется на противоположный.

Рассмотрим применение данного алгоритма на решении примеров.

Решить неравенство вида 3 · x + 12 ≤ 0 .

Данное линейное неравенство имеет a = 3 и b = 12 . Значит, коэффициент a при x не равен нулю. Применим выше сказанные алгоритмы, решим.

Необходимо перенести слагаемое 12 в другую часть неравенства с изменением знака перед ним. Тогда получаем неравенство вида 3 · x ≤ − 12 . Необходимо произвести деление обеих частей на 3 . Знак не поменяется, так как 3 является положительным числом. Получаем, что ( 3 · x ) : 3 ≤ ( − 12 ) : 3 , что даст результат x ≤ − 4 .

Неравенство вида x ≤ − 4 является равносильным. То есть решение для 3 · x + 12 ≤ 0 – это любое действительное число, которое меньше или равно 4 . Ответ записывается в виде неравенства x ≤ − 4 , или числового промежутка вида ( − ∞ , − 4 ] .

Весь выше прописанный алгоритм записывается так:

3 · x + 12 ≤ 0 ; 3 · x ≤ − 12 ; x ≤ − 4 .

Ответ: x ≤ − 4 или ( − ∞ , − 4 ] .

Указать все имеющиеся решения неравенства − 2 , 7 · z > 0 .

Из условия видим, что коэффициент a при z равняется — 2 , 7 , а b в явном виде отсутствует или равняется нулю. Первый шаг алгоритма можно не использовать, а сразу переходить ко второму.

Производим деление обеих частей уравнения на число — 2 , 7 . Так как число отрицательное, необходимо поменять знак неравенства на противоположный. То есть получаем, что ( − 2 , 7 · z ) : ( − 2 , 7 ) 0 : ( − 2 , 7 ) , и дальше z 0 .

Весь алгоритм запишем в краткой форме:

− 2 , 7 · z > 0 ; z 0 .

Ответ: z 0 или ( − ∞ , 0 ) .

Решить неравенство — 5 · x — 15 22 ≤ 0 .

По условию видим, что необходимо решить неравенство с коэффициентом a при переменной x , которое равняется — 5 , с коэффициентом b , которому соответствует дробь — 15 22 . Решать неравенство необходимо, следуя алгоритму, то есть: перенести — 15 22 в другую часть с противоположным знаком, разделить обе части на — 5 , изменить знак неравенства:

— 5 · x ≤ 15 22 ; — 5 · x : — 5 ≥ 15 22 : — 5 x ≥ — 3 22

При последнем переходе для правой части используется правило деления числе с разными знаками 15 22 : — 5 = — 15 22 : 5 , после чего выполняем деление обыкновенной дроби на натурально число — 15 22 : 5 = — 15 22 · 1 5 = — 15 · 1 22 · 5 = — 3 22 .

Ответ: x ≥ — 3 22 и [ — 3 22 + ∞ ) .

Рассмотрим случай, когда а = 0 . Линейное выражение вида a · x + b 0 является неравенством 0 · x + b 0 , где на рассмотрение берется неравенство вида b 0 , после чего выясняется, оно верное или нет.

Все основывается на определении решения неравенства. При любом значении x получаем числовое неравенство вида b 0 , потому что при подстановке любого t вместо переменной x , тогда получаем 0 · t + b 0 , где b 0 . В случае, если оно верно, то для его решения подходит любое значение. Когда b 0 неверно, тогда линейное уравнение не имеет решений, потому как не имеется ни одного значения переменной, которое привело бы верному числовому равенству.

Все суждения рассмотрим в виде алгоритма решения линейных неравенств 0 · x + b 0 ( ≤ , > , ≥ ) :

Числовое неравенство вида b 0 ( ≤ , > , ≥ ) верно, тогда исходное неравенство имеет решение при любом значении, а неверно тогда, когда исходное неравенство не имеет решений.

Решить неравенство 0 · x + 7 > 0 .

Данное линейное неравенство 0 · x + 7 > 0 может принимать любое значение x . Тогда получим неравенство вида 7 > 0 . Последнее неравенство считается верным, значит любое число может быть его решением.

Найти решение неравенства 0 · x − 12 , 7 ≥ 0 .

При подстановке переменной x любого числа получим, что неравенство получит вид − 12 , 7 ≥ 0 . Оно является неверным. То есть 0 · x − 12 , 7 ≥ 0 не имеет решений.

Ответ: решений нет.

Рассмотрим решение линейных неравенств , где оба коэффициента равняется нулю.

Определить не имеющее решение неравенство из 0 · x + 0 > 0 и 0 · x + 0 ≥ 0 .

При подстановке любого числа вместо x получим два неравенства вида 0 > 0 и 0 ≥ 0 . Первое является неверным. Значит, 0 · x + 0 > 0 не имеет решений, а 0 · x + 0 ≥ 0 имеет бесконечное количество решений, то есть любое число.

Ответ: неравенство 0 · x + 0 > 0 не имеет решений, а 0 · x + 0 ≥ 0 имеет решения.

Видео:Урок по теме РЕШЕНИЕ НЕРАВЕНСТВ С ОДНОЙ ПЕРЕМЕННОЙСкачать

Методом интервалов

Данный метод рассматривается в школьном курсе математики. Метод интервалов способен разрешать различные виды неравенств, также и линейные.

Метод интервалов применяется для линейных неравенств при значении коэффициента x не равному 0 . Иначе придется вычислять при помощи другого метода.

Метод интервалов – это:

• введение функции y = a · x + b ;
• поиск нулей для разбивания области определения на промежутки;
• определение знаков для понятия их на промежутках.

Соберем алгоритм для решения линейных уравнений a · x + b 0 ( ≤ , > , ≥ ) при a ≠ 0 с помощью метода интервалов:

• нахождение нулей функции y = a · x + b , чтобы решить уравнение вида a · x + b = 0 . Если a ≠ 0 , тогда решением будет единственный корень, который примет обозначение х 0 ;
• построение координатной прямой с изображением точки с координатой х 0 , при строгом неравенстве точка обозначается выколотой, при нестрогом – закрашенной;
• определение знаков функции y = a · x + b на промежутках, для этого необходимо находить значения функции в точках на промежутке;
• решение неравенства со знаками > или ≥ на координатной прямой добавляется штриховка над положительным промежутком, или ≤ над отрицательным промежутком.

Рассмотрим несколько примеров решения линейного неравенства при помощи метода интервалов.

Решить неравенство − 3 · x + 12 > 0 .

Из алгоритма следует, что для начала нужно найти корень уравнения − 3 · x + 12 = 0 . Получаем, что − 3 · x = − 12 , x = 4 . Необходимо изобразить координатную прямую, где отмечаем точку 4 . Она будет выколотой, так как неравенство является строгим. Рассмотрим чертеж, приведенный ниже.

Нужно определить знаки на промежутках. Чтобы определить его на промежутке ( − ∞ , 4 ) , необходимо произвести вычисление функции y = − 3 · x + 12 при х = 3 . Отсюда получим, что − 3 · 3 + 12 = 3 > 0 . Знак на промежутке является положительным.

Определяем знак из промежутка ( 4 , + ∞ ) , тогда подставляем значение х = 5 . Имеем, что − 3 · 5 + 12 = − 3 0 . Знак на промежутке является отрицательным. Изобразим на числовой прямой, приведенной ниже.

Мы выполняем решение неравенства со знаком > , причем штриховка выполняется над положительным промежутком. Рассмотрим чертеж, приведенный ниже.

Из чертежа видно, что искомое решение имеет вид ( − ∞ , 4 ) или x 4 .

Ответ: ( − ∞ , 4 ) или x 4 .

Видео:ЛИНЕЙНЫЕ НЕРАВЕНСТВА - Как решать линейные неравенства // Подготовка к ЕГЭ по МатематикеСкачать

Графическим способом

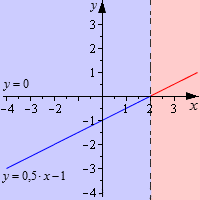
Чтобы понять, как изображать графически, необходимо рассмотреть на примере 4 линейных неравенства: 0 , 5 · x − 1 0 , 0 , 5 · x − 1 ≤ 0 , 0 , 5 · x − 1 > 0 и 0 , 5 · x − 1 ≥ 0 . Их решениями будут значения x 2 , x ≤ 2 , x > 2 и x ≥ 2 . Для этого изобразим график линейной функции y = 0 , 5 · x − 1 , приведенный ниже.

• решением неравенства 0 , 5 · x − 1 0 считается промежуток, где график функции y = 0 , 5 · x − 1 располагается ниже О х ;
• решением 0 , 5 · x − 1 ≤ 0 считается промежуток, где функция y = 0 , 5 · x − 1 ниже О х или совпадает;
• решением 0 , 5 · x − 1 > 0 считается промежуток, гре функция располагается выше О х ;
• решением 0 , 5 · x − 1 ≥ 0 считается промежуток, где график выше О х или совпадает.

Смысл графического решения неравенств заключается в нахождении промежутков, которое необходимо изображать на графике. В данном случае получаем, что левая часть имеет y = a · x + b , а правая – y = 0 , причем совпадает с О х .

Видео:8 класс, 40 урок, Решение линейных неравенствСкачать

Алгоритм решения линейных неравенств графическим способом.

Построение графика функции y = a · x + b производится:

• во время решения неравенства a · x + b 0 определяется промежуток, где график изображен ниже О х ;
• во время решения неравенства a · x + b ≤ 0 определяется промежуток, где график изображается ниже оси О х или совпадает;
• во время решения неравенства a · x + b > 0 производится определение промежутка, где график изображается выше О х ;
• во время решения неравенства a · x + b ≥ 0 производится определение промежутка, где график находится выше О х или совпадает.

Решить неравенство — 5 · x — 3 > 0 при помощи графика.

Необходимо построить график линейной функции — 5 · x — 3 > 0 . Данная прямая является убывающей, потому как коэффициент при x является отрицательным. Для определения координат точки его пересечения с О х — 5 · x — 3 > 0 получим значение — 3 5 . Изобразим графически.

Решение неравенства со знаком > , тогда необходимо обратить внимание на промежуток выше О х . Выделим красным цветом необходимую часть плоскости и получим, что

Необходимый промежуток является частью О х красного цвета. Значит, открытый числовой луч — ∞ , — 3 5 будет решением неравенства. Если бы по условию имели нестрогое неравенство, тогда значение точки — 3 5 также являлось бы решением неравенства. И совпадало бы с О х .

Ответ: — ∞ , — 3 5 или x — 3 5 .

Графический способ решения используется, когда левая часть будет отвечать функции y = 0 · x + b , то есть y = b . Тогда прямая будет параллельна О х или совпадающей при b = 0 . Эти случаю показывают, что неравенство может не иметь решений, либо решением может быть любое число.

Определить из неравенств 0 · x + 7 = 0 , 0 · x + 0 ≥ 0 то, которое имеет хотя бы одно решение.

Представление y = 0 · x + 7 является y = 7 , тогда будет задана координатная плоскость с прямой, параллельной О х и находящейся выше О х . Значит, 0 · x + 7 = 0 решений не имеет, потому как нет промежутков.

График функции y = 0 · x + 0 , считается y = 0 , то есть прямая совпадает с О х . Значит, неравенство 0 · x + 0 ≥ 0 имеет множество решений.

Ответ: второе неравенство имеет решение при любом значении x .

Видео:ЛИНЕЙНЫЕ УРАВНЕНИЯ - Как решать линейные уравнения // Подготовка к ЕГЭ по МатематикеСкачать

Неравенства, сводящиеся к линейным

Решение неравенств можно свести к решению линейного уравнения, которые называют неравенствами, сводящимися к линейным.

Данные неравенства были рассмотрены в школьном курсе, так как они являлись частным случаем решения неравенств, что приводило к раскрытию скобок и приведению подобных слагаемых. Для примера рассмотрим, что 5 − 2 · x > 0 , 7 · ( x − 1 ) + 3 ≤ 4 · x − 2 + x , x — 3 5 — 2 · x + 1 > 2 7 · x .

Неравенства, приведенные выше, всегда приводятся к виду линейного уравнения. После чего раскрываются скобки и приводятся подобные слагаемые, переносятся из разных частей, меняя знак на противоположный.

При сведении неравенства 5 − 2 · x > 0 к линейному, представляем его таким образом, чтобы оно имело вид − 2 · x + 5 > 0 , а для приведения второго получаем, что 7 · ( x − 1 ) + 3 ≤ 4 · x − 2 + x . Необходимо раскрыть скобки, привести подобные слагаемые, перенести все слагаемые в левую часть и привести подобные слагаемые. Это выглядит таким образом:

7 · x − 7 + 3 ≤ 4 · x − 2 + x 7 · x − 4 ≤ 5 · x − 2 7 · x − 4 − 5 · x + 2 ≤ 0 2 · x − 2 ≤ 0

Это приводит решение к линейному неравенству.

Эти неравенства рассматриваются как линейные, так как имеют такой же принцип решения, после чего возможно приведение их к элементарным неравенствам.

Для решения такого вида неравенства такого вида необходимо свести его к линейному. Это следует делать таким образом:

• раскрыть скобки;
• слева собрать переменные, а справа числа;
• привести подобные слагаемые;
• разделить обе части на коэффициент при x .

Решить неравенство 5 · ( x + 3 ) + x ≤ 6 · ( x − 3 ) + 1 .

Производим раскрытие скобок, тогда получим неравенство вида 5 · x + 15 + x ≤ 6 · x − 18 + 1 . После приведения подобных слагаемых имеем, что 6 · x + 15 ≤ 6 · x − 17 . После перенесения слагаемых с левой в правую, получим, что 6 · x + 15 − 6 · x + 17 ≤ 0 . Отсюда имеет неравенство вида 32 ≤ 0 из полученного при вычислении 0 · x + 32 ≤ 0 . Видно, что неравенство неверное, значит, неравенство, данное по условию, не имеет решений.

Ответ: нет решений.

Стоит отметить, что имеется множество неравенств другого вида, которые могут сводится к линейному или неравенству вида, показанного выше. Например, 5 2 · x − 1 ≥ 1 является показательным уравнением, которое сводится к решению линейного вида 2 · x − 1 ≥ 0 . Эти случаи будут рассмотрены при решении неравенств данного вида.

Видео:Решение системы линейных неравенств с одной переменной. 6 класс.Скачать

Решение линейных неравенств

О чем эта статья:

Видео:Неравенства с двумя переменными. 9 класс.Скачать

Основные понятия

Алгебра не всем дается легко с первого раза. Чтобы не запутаться во всех темах и правилах, важно изучать темы последовательно и по чуть-чуть. Сегодня узнаем, как решать линейные неравенства.

Неравенство — это алгебраическое выражение, в котором используются знаки ≠, , ≤, ≥.

Линейные неравенства — это неравенства вида:

где a и b — любые числа, a ≠ 0, x — неизвестная переменная. Как решаются неравенства рассмотрим далее в статье.

Решение — значение переменной, при котором неравенство становится верным.

Решить неравенство значит найти все значения переменной, при которой неравенство верное.

Видео:Линейное неравенство с одной переменной. 6 класс.Скачать

Типы неравенств

1. Строгие — используют только больше (>) или меньше ( b — это значит, что a больше, чем b.
2. a > b и b > и

Видео:Подготовка к ОГЭ . Рациональные неравенства | Математика | TutorOnlineСкачать

Линейные неравенства: свойства и правила

Вспомним свойства числовых неравенств:

1. Если а > b , то b а.
2. Если а > b и b > c, то а > c. И также если а b, то а + c > b+ c (и а – c > b – c).

Если же а b и c > d, то а + c > b + d.

Если а 8 почленно вычесть 3 > 2, получим верный ответ 9 > 6. Если из 12 > 8 почленно вычесть 7 > 2, то полученное будет неверным.

Если а d, то а – c b, m — положительное число, то mа > mb и

Обе части можно умножить или разделить на одно положительное число (знак при этом остаётся тем же).

Если же а > b, n — отрицательное число, то nа

Обе части можно умножить или разделить на одно отрицательное число, при этом знак неравенства поменять на противоположный.

1. Если а > b и c > d, где а, b, c, d > 0, то аc > bd.

Если а 0, то аc b, где а, b > 0, то а2 > b2, и если а b, где а, b > 0, то
b» height=»45″ src=»https://lh5.googleusercontent.com/MuRDPQeqxIZvVG_mHVaktFp6nlIEEbz8zdRs1ZW8CZbZacJrS4aKzrDyhKxXpJvc35TSAgiRpqr-63sGzL9_sPU80vFhR0ZDAmSmRFZtwEldDkWRttfSGuaJJIb7xWxZDugU3xTt»>

Решением неравенства с одной переменной называется значение переменной, которое трансформирует его в верное числовое неравенство.

Чтобы упростить процесс нахождения корней неравенства, нужно провести равносильные преобразования — то заменить данное неравенство более простым. При этом все решения должны быть сохранены без возникновения посторонних корней.

Свойства выше помогут нам использовать следующие правила.

Видео:Как решать неравенства? Математика 10 класс | TutorOnlineСкачать

Правила линейных неравенств

1. Любой член можно перенести из одной части в другую с противоположным знаком. Знак неравенства при этом не меняется.

• 2x − 3 > 6 ⇒ 2x > 6 + 3 ⇒ 2x > 9.

1. Обе части можно умножить или разделить на одно положительное число. Знак неравенства при этом не меняется.

• Умножим обе части на пять 2x > 9 ⇒ 10x > 45.

1. Обе части можно умножить или разделить на одно отрицательное число. Знак неравенства при этом меняется на противоположный.

• Разделим обе части на минус два 2x > 9 ⇒ 2x : (–2) > 9 : (–2) ⇒ x
  

  Видео:Линейные неравенства. Решение линейных неравенств с одной переменной. Числовые промежутки. Алгебра 9Скачать

  

  Решение линейных неравенств

  Линейные неравенства с одной переменной x выглядят так:

  где a и b — действительные числа. А на месте x может быть обычное число.

  Видео:Система уравнений VS Система неравенств. ОГЭ по математике №9, 13| Математика TutorOnlineСкачать

  

  Равносильные преобразования

  Для решения ax + b , ≥) нужно применить равносильные преобразования неравенства. Рассмотрим два случая: когда коэффициент равен и не равен нулю.

  Алгоритм решения ax + b , ≥) является верным, когда исходное имеет решение при любом значении. Неверно тогда, когда исходное не имеет решений.

  Рассмотрим пример: 0 * x + 5 > 0.

  Как решаем:

  • Данное неравенство 0 * x + 5 > 0 может принимать любое значение x.
  • Получается верное числовое неравенство 5 > 0. Значит его решением может быть любое число.

  Видео:Решение системы неравенствСкачать

  

  Метод интервалов

  Метод интервалов можно применять для линейных неравенств, когда значение коэффициента x не равно нулю.

  Метод интервалов заключается в следующем:

  • вводим функцию y = ax + b;
  • ищем нули для разбиения области определения на промежутки;
  • отмечаем полученные корни на координатной прямой;
  • определяем знаки и отмечаем их на интервалах.

  Алгоритм решения ax + b , ≥) при a ≠ 0 с использованием метода интервалов:

  • найдем нули функции y = ax + b для решения уравнения ax + b = 0.

  Если a ≠ 0, тогда решением будет единственный корень — х₀;

  • начертим координатную прямую с изображением точки с координатой х₀, при строгом неравенстве точку рисуем выколотой, при нестрогом — закрашенной;
  • определим знаки функции y = ax + b на промежутках.

  Для этого найдем значения функции в точках на промежутке;

  если решение неравенства со знаками > или ≥ — добавляем штриховку над положительным промежутком на координатной прямой, если 0.

  Как решаем:

  В соответствии с алгоритмом, сначала найдем корень уравнения − 6x + 12 = 0,

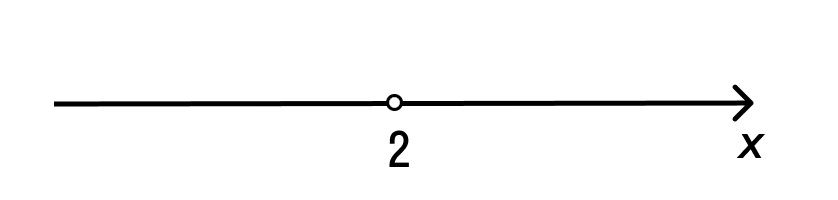
  Изобразим координатную прямую с отмеченной выколотой точкой, так как неравенство является строгим.

  

  Определим знаки на промежутках.

  Чтобы определить на промежутке (−∞, 2), необходимо вычислить функцию y = −6x + 12 при х = 1. Получается, что −6 * 1 + 12 = 6, 6 > 0. Знак на промежутке является положительным.

  Определяем знак на промежутке (2, + ∞) , тогда подставляем значение х = 3. Получится, что −6 * 3 + 12 = − 6, − 6

  Видео:Линейное неравенство с одной переменной. 6 класс.Скачать

  

  Графический способ

  Смысл графического решения неравенств заключается в том, чтобы найти промежутки, которые необходимо изобразить на графике.

  Алгоритм решения y = ax + b графическим способом

  • во время решения ax + b 0 определить промежуток, где график изображается выше Ох;
  • во время решения ax + b ≥ 0 определить промежуток, где график находится выше оси Ох или совпадает.

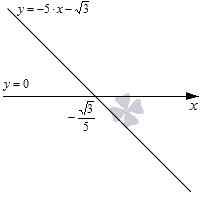
  Рассмотрим пример: −5 * x − √3 > 0.

  Как решаем

  • Так как коэффициент при x отрицательный, данная прямая является убывающей.
  • Координаты точки пересечения с Ох равны (−√3 : 5; 0).
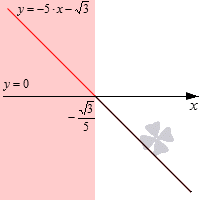
  • Неравенство имеет знак >, значит нужно обратить внимание на промежуток выше оси Ох.
  • Поэтому открытый числовой луч (−∞, −√3 : 5) будет решением.

  Ответ: (−∞, −√3 : 5) или x

  Видео:Алгебра 9. Урок 4 - Неравенства линейные - решение.Скачать

  

  Учебное пособие «Методика обучения решению линейных неравенств с одной переменной»

  Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

  Рабочие листы и материалы для учителей и воспитателей

  Более 2 500 дидактических материалов для школьного и домашнего обучения

  « Методика обучения решению линейных неравенств с одной переменной »

  исполнила учитель математики МБОУ СОШ»Лидер-2»

  Драгунова Елена Геннадьевна

  Г.Находка Приморский край

  2. Методическая особенность темы «Линейные неравенства с одной переменной».

  3. Разработка урока по теме « Линейные неравенства».

  4. Список литературы .

  Аксиома современной школы – раскрытие способностей каждого ученика, воспитание личности, готовой к жизни в высокотехнологичном и конкурентном мире. Есть несколько условий для ее воплощения в жизнь: адаптивность систем образования к особенностям развития и подготовки учащихся; равный доступ молодых людей к полноценному образованию в соответствии с их интересами и склонностями, независимо от материального достатка семьи, места проживания и национальной принадлежности.

  Учебная деятельность, позволяющая сформировать у подростков стремление к саморазвитию и самосовершенствованию, имеет свои особенности: работа по модифицированным программам; блочный метод построения программного материала; входная, текущая, итоговая диагностика уровня обученности; зачетная система контроля и учета знаний, расширяющая возможности индивидуальной работы; метод « погружения» в предмет.

  М етодические особенности темы « Линейные неравенства»

  Тема «Линейные неравенства с одной переменной» изучается в 8 классе

  Учебник Алгебра 8 класс. Авторы: Ю.Н.Макарычев, Н.Г. Миндюк,

  К.И. Нешков, С.Б. Суворова.

  На изучение темы отводится 4 урока

  Основная учебно-познавательная цель : Сформировать умение решать линейные неравенства с одной переменной.

  Перед объяснением нового материала необходимо повторить понятие числовых промежутков, используя геометрическую интерпретацию понятий «больше» и «меньше». Повторение можно провести в устных упражнениях с использованием таблицы или при выполнении математического диктанта. Рекомендуется включить упражнения как на непосредственное чтение промежутков, определение наибольшего и наименьшего целых значений в данных промежутках, так и на переход от простейших неравенств к геометрической интерпретации их в виде числовых промежутков. Можно повторение провести в виде математического диктанта.

  Затем перейти к новому материалу: ввести определение линейного неравенства с одной переменной , определение строгого и нестрогого неравенства, определение решения неравенства , что значит решить неравенство . Определение равносильных неравенств разъяснить на примерах. Затем перечислить свойства неравенств . Алгоритм решения линейных неравенств, содержащих одну переменную сходен с решением линейных уравнений. Единственная сложность – деление обеих частей неравенства на отрицательное число. Чтобы ученики поняли, почему меняется знак неравенства при делении на отрицательное число, можно поступить следующим образом: написать на доске «неверное» решение:

  -2х > 4; х > -2 и убедиться, что числа из промежутка (-2;+∞) не являются решениям данного неравенства, а вот числа, из промежутка (-∞; -2) являются решениями. А как можно получить этот промежуток в решении? Надо взять симметричный промежуток –(-∞;-2). А как его получить без этих лишних действий? Надо поменять знак неравенства при делении на отрицательное число и ответ сразу будет верным. Можно рассмотреть еще несколько аналогичных примеров и убедиться, что это так.

  Навык получения неравенства, равносильного данному при делении (умножении) на отрицательное число формируется путем решения большого числа устных упражнений. Этой цели могут служить упражнения типа:

  -2х -4; -2х 12; -х -12; -х ≤ 0; -х ≥4.

  Затем решаются неравенства и показывается, что решения его на координатной прямой изображаются в виде луча или открытого луча.

  Но решением неравенства может служить также числовая прямая и пустое множество.

  На конкретных примерах рассматриваются решения неравенств ах > b ;

  ах b при а=0. Например, 0х -7 неверно при любом значении х, т. е. неравенство не имеет решений.

  Убедившись, что основной навык решения линейных неравенств с одной переменной сформирован, можно переходить к более сложным неравенствам, способствующим дальнейшему совершенствованию навыков тождественных преобразований.

  На резервных уроках, на факультативных занятиях и при подготовке к итоговой аттестации можно рассмотреть более сложные неравенства, доказательство неравенств, текстовые задачи и задания с параметром.

  Приобретенные учащимися умения в решении и доказательстве неравенств находит применение при рассмотрении свойств функций.

  При изучении темы «Применение неравенств для изучения свойств функций» даются понятия о возрастании и убывании функции и промежутках знакопостоянства. Важно сформировать у учащихся понимание того, что при ответе на вопрос «При каких значениях х f(х) > 0 ( f(х)

  Методическая разработка урока

  Обучающая : ввести определение линейного неравенства с одной переменной, определение равносильных неравенств и основных свойств неравенств, используемых при решении, и показать их применение при решении неравенств, закрепить умения учащихся изображать промежуток на координатной прямой.

  Развивающая : Развитие внимания, умение выделять главное, формирование графической культуры оформления чертежей.

  Воспитательная : воспитание трудолюбия, аккуратности, самостоятельности.

  Оборудование : интерактивная доска, учебник, доска, мел.

  I. Устные упражнения (слайды на экране интерактивной доски)

  1. Прочитайте неравенство и назовите соответствующий ему промежуток:

  а) х ≤ -3; б) х ≥ 7; в) -1 ≤ х ≤ 1; г) -2 ≤ х ≤ 3; д) х ≤ -5; е) х ≥12.

  2.Принадлежит ли промежутку (-2; 7,5) число -3; -2; 0; 4.6; 7; 7,5?

  3. Укажите наибольшее и наименьшее целое число, принадлежащее промежутку: а) [-8;5]; б) [-1; 6); в) (-∞; 9]; г) (4; +∞); д) (-3; -2)

  II. Изучение нового материала

  1. Рассмотрим неравенство с одной переменной 3х – 1 >5. Это неравенство при одних значениях х обращается в верное числовое неравенство (например, при х=3; 9; 10,5; 52), при других – не является верным (например, при = 0; -4; -11; 2) . Говорят, что числа 3; 9; 10,5; 52 являются решениями данного неравенства, а числа 0; -4; -11; 2 не являются его решениями.

  2. Что же является решением неравенства ? Дать определение.

  3. Что значит решить неравенство ? Дать определение.

  4. Как найти все решения неравенства?

  Линейные неравенства решают почти так же, как и линейные уравнения. Вызвать к доске ученика решить линейное уравнение 3х – 1 =5. Затем рядом с решением ученика учитель пишет решение неравенств 3х – 1 равносильных неравенств . Правила, которые использовались при решении неравенств, вытекают из свойств неравенств и позволяют выполнять преобразования, приводящие к равносильному неравенству.

  Итак, при решении линейного неравенства используются следующие свойства . Перечислить. Прочитать по учебнику. (На экране основные определения и свойства равносильных неравенств)

  5. Показать решение неравенства 1) 5х + 10 >3х + 2

  .Показать множество решений на рисунке

  4у -8 ≥ 5у – 15; 4у – 5у ≥ -15 + 8; -у ≥ -7; у ≤ 7

  Прежде, чем поменять знак неравенства можно подобрать несколько решений и «догадаться», что решением будут все числа, меньшие или равные 7, т.е. промежуток (-∞; 7].

  Итак, все решения линейного неравенства на координатной прямой изображаются в виде луча или открытого луча.

  🎥 Видео

  Урок на тему РЕШЕНИЕ СИСТЕМ НЕРАВЕНСТВ С ОДНОЙ ПЕРЕМЕННОЙ 8 КЛАСССкачать

  

  Урок 7 ЛИНЕЙНОЕ УРАВНЕНИЕ С ОДНОЙ ПЕРЕМЕННОЙСкачать

  

  Решение квадратных неравенств | МатематикаСкачать