Решение линейных и квадратных уравнений и неравенств с одной переменной

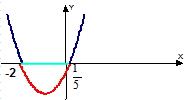
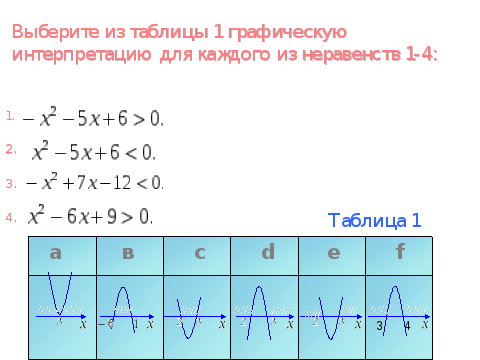
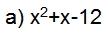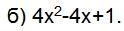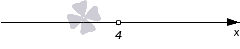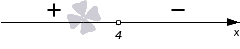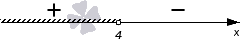Смотрите бесплатные видео-уроки по теме “Неравенства” на канале Ёжику Понятно.

Видео-уроки на канале Ёжику Понятно. Подпишись!

Содержание страницы:

• Неравенства

• Линейные неравенства

Видео:Решение квадратных неравенств | МатематикаСкачать

Неравенства

Что такое неравенство? Если взять любое уравнение и знак = поменять на любой из знаков неравенства:

≥ больше или равно,

≤ меньше или равно,

то получится неравенство.

Линейные неравенства

Линейные неравенства – это неравенства вида:

a x b a x ≤ b a x > b a x ≥ b

где a и b – любые числа, причем a ≠ 0, x – переменная.

Примеры линейных неравенств:

3 x 5 x − 2 ≥ 0 7 − 5 x 1 x ≤ 0

Решить линейное неравенство – получить выражение вида:

x c x ≤ c x > c x ≥ c

где c – некоторое число.

Последний шаг в решении неравенства – запись ответа. Давайте разбираться, как правильно записывать ответ.

• Если знак неравенства строгий > , , точка на оси будет выколотой (не закрашенной), а скобка, обнимающая точку – круглой .

Смысл выколотой точки в том, что сама точка в ответ не входит.

• Если знак неравенства нестрогий ≥ , ≤ , точка на оси будет жирной (закрашенной), а скобка, обнимающая точку – квадратной .

Смысл жирной точки в том, что сама точка входит в ответ.

• Скобка, которая обнимает знак бесконечности всегда круглая – не можем мы объять необъятное, как бы нам этого ни хотелось.

Таблица числовых промежутков

//mailru,yandex,google,vkontakte,odnoklassniki,instagram,wargaming,facebook,twitter,liveid,steam,soundcloud,lastfm, // echo( ‘

Видео:Как понять неравенства? Квадратные неравенства. Линейные и сложные неравенства | TutorOnlineСкачать

Калькулятор онлайн.
Решение неравенств: линейные, квадратные и дробные.

Программа решения неравенств не просто даёт ответ задачи, она приводит подробное решение с пояснениями, т.е. отображает процесс решения для того чтобы проконтролировать знания по математике и/или алгебре.

Причём, если в процессе решения неравенства нужно решить, например, квадратное уравнение, то его подробное решение также выводится (оно заключается в спойлер).

Данная программа может быть полезна учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.

Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.

В качестве переменной может выступать любая латинсая буква.
Например: ( x, y, z, a, b, c, o, p, q ) и т.д.

Числа можно вводить целые или дробные.
Причём, дробные числа можно вводить не только в виде десятичной, но и в виде обыкновенной дроби.

Правила ввода десятичных дробей.
В десятичных дробях дробная часть от целой может отделяться как точкой так и запятой.
Например, можно вводить десятичные дроби так: 2.5x — 3,5x^2

Правила ввода обыкновенных дробей.
В качестве числителя, знаменателя и целой части дроби может выступать только целое число.

Знаменатель не может быть отрицательным.

При вводе числовой дроби числитель отделяется от знаменателя знаком деления: /
Целая часть отделяется от дроби знаком амперсанд: &
Ввод: 3&1/3 — 5&6/5y +1/7y^2
Результат: ( 3frac — 5frac y + fracy^2 )

При вводе выражений можно использовать скобки. В этом случае при решении неравенства выражения сначала упрощаются.
Например: 5(a+1)^2+2&3/5+a > 0,6(a-2)(a+3)

Нажмите на кнопку для изменения типа неравенства.

Выберите нужный знак неравенства и введите многочлены в поля ниже.
Решить неравенство

Видео:Как решать неравенства? Часть 1| МатематикаСкачать

Немного теории.

Сравнивать величины и количества при решении практических задач приходилось ещё с древних времён. Тогда же появились и такие слова, как больше и меньше, выше и ниже, легче и тяжелее, тише и громче, дешевле и дороже и т.д., обозначающие результаты сравнения однородных величин.

Понятия больше и меньше возникли в связи со счётом предметов, измерением и сравнением величин. Например, математики Древней Греции знали, что сторона любого треугольника меньше суммы двух других сторон и что против большего угла в треугольнике лежит большая сторона. Архимед, занимаясь вычислением длины окружности, установил, что периметр всякого круга равен утроенному диаметру с избытком, который меньше седьмой части диаметра, но больше десяти семьдесят первых диаметра.

Символически записывать соотношения между числами и величинами с помощью знаков > и b. Записи, в которых два числа соединены одним из знаков: > (больше), frac ) верное числовое неравенство, 0,23 > 0,235 — неверное числовое неравенство.

Неравенства, в которые входят неизвестные, могут быть верными при одних значениях неизвестных и неверными при других. Например, неравенство 2x+1>5 верное при х = 3, а при х = -3 — неверное. Для неравенства с одним неизвестным можно поставить задачу: решить неравенство. Задачи решения неравенств на практике ставятся и решаются не реже, чем задачи решения уравнений. Например, многие экономические проблемы сводятся к исследованию и решению систем линейных неравенств. Во многих разделах математики неравенства встречаются чаще, чем уравнения.

Некоторые неравенства служат единственным вспомогательным средством, позволяющим доказать или опровергнуть существование определённого объекта, например, корня уравнения.

Далее вы узнаете свойства неравенств, научитесь решать неравенства. Полученные умения вам понадобятся при изучении последующего материала, для решения практических задач, а также задач физики и геометрии.

Видео:8 класс, 40 урок, Решение линейных неравенствСкачать

Числовые неравенства

Вы умеете сравнивать целые числа, десятичные дроби. Знаете правила сравнения обыкновенных дробей с одинаковыми знаменателями, но разными числителями; с одинаковыми числителями, но разными знаменателями. Здесь вы научитесь сравнивать любые два числа с помощью нахождения знака их разности.

Сравнение чисел широко применяется на практике. Например, экономист сравнивает плановые показатели с фактическими, врач сравнивает температуру больного с нормальной, токарь сравнивает размеры вытачиваемой детали с эталоном. Во всех таких случаях сравниваются некоторые числа. В результате сравнения чисел возникают числовые неравенства.

Определение. Число а больше числа b, если разность а-b положительна. Число а меньше числа b, если разность а-b отрицательна.

Если а больше b, то пишут: а > b; если а меньше b, то пишут: а b означает, что разность а — b положительна, т.е. а — b > 0. Неравенство а b, a = b, a , = или b и b > с, то а > с.

Теорема. Если к обеим частям неравенства прибавить одно и то же число, то знак неравенства не изменится.
Следствие. Любое слагаемое можно перенести из одной части неравенства в другую, изменив знак этого слагаемого на противоположный.

Теорема. Если обе части неравенства умножить на одно и то же положительное число, то знак неравенства не изменится. Если обе части неравенства умножить на одно и то же отрицательное число, то знак неравенства изменится на противоположный.
Следствие. Если обе части неравенства разделить на одно и то же положительное число, то знак неравенства не изменится. Если обе части неравенства разделить на одно и то же отрицательное число, то знак неравенства изменится на противоположный.

Вы знаете, что числовые равенства можно почленно складывать и умножать. Далее вы научитесь выполнять аналогичные действия с неравенствами. Умения почленно складывать и умножать неравенства часто применяются на практике. Эти действия помогают решать задачи оценивания и сравнения значений выражений.

При решении различных задач часто приходится складывать или умножать почленно левые и правые части неравенств. При этом иногда говорят, что неравенства складываются или умножаются. Например, если турист прошёл в первый день более 20 км, а во второй — более 25 км, то можно утверждать, что за два дня он прошёл более 45 км. Точно так же если длина прямоугольника меньше 13 см, а ширина меньше 5 см, то можно утверждать, что площадь этого прямоугольника меньше 65 см2.

При рассмотрении этих примеров применялись следующие теоремы о сложении и умножении неравенств:

Теорема. При сложении неравенств одинакового знака получается неравенство того же знака: если а > b и c > d, то a + c > b + d.

Теорема. При умножении неравенств одинакового знака, у которых левые и правые части положительны, получается неравенство того же знака: если а > b, c > d и а, b, с, d — положительные числа, то ac > bd.

Неравенства со знаком > (больше) и 1/2, 3/4 b, c и и b, quad ax

Видео:Линейное неравенство с одной переменной. 6 класс.Скачать

Решение неравенств второй степени с одной переменной

Неравенства вида
( ax^2+bx+c >0 ) и ( ax^2+bx+c 0 ) или ( ax^2+bx+c 0 или вниз при a 0 или в нижней при a 0 ) ) или ниже оси x (если решают неравенство
( ax^2+bx+c

Видео:Решение квадратных неравенств методом интервалов. 8 класс.Скачать

Решение неравенств методом интервалов

Рассмотрим функцию
f(x) = (х + 2)(х — 3)(х — 5)

Областью определения этой функции является множество всех чисел. Нулями функции служат числа -2, 3, 5. Они разбивают область определения функции на промежутки ( (-infty; -2), ; (-2; 3), ; (3; 5) ) и ( (5; +infty) )

Выясним, каковы знаки этой функции в каждом из указанных промежутков.

Выражение (х + 2)(х — 3)(х — 5) представляет собой произведение трех множителей. Знак каждого из этих множителей в рассматриваемых промежутках указан в таблице:

Неравенство	Графическое решение	Форма записи ответа
x c	x ∈ ( − ∞ ; c )
x ≤ c		x ∈ ( − ∞ ; c ]
x > c		x ∈ ( c ; + ∞ )
x ≥ c	Алгоритм решения линейного неравенства Раскрыть скобки (если они есть), перенести иксы в левую часть, числа в правую и привести подобные слагаемые. Должно получиться неравенство одного из следующих видов: a x b a x ≤ b a x > b a x ≥ b Пусть получилось неравенство вида a x ≤ b. Для того, чтобы его решить, необходимо поделить левую и правую часть неравенства на коэффициент a. Если a > 0 то неравенство приобретает вид x ≤ b a . Если a 0 , то знак неравенства меняется на противоположный , неравенство приобретает вид x ≥ b a . Записываем ответ в соответствии с правилами, указанными в таблице числовых промежутков. Примеры решения линейных неравенств: №1. Решить неравенство 3 ( 2 − x ) > 18. Решение: Раскрываем скобки, переносим иксы влево, числа вправо, приводим подобные слагаемые. − 3 x > 18 − 6 − 3 x > 12 | ÷ ( − 3 ) Делим обе части неравенства на ( -3 ) – коэффициент, который стоит перед x . Так как − 3 0 , знак неравенства поменяется на противоположный . x 12 − 3 ⇒ x − 4 Остается записать ответ (см. таблицу числовых промежутков). Ответ: x ∈ ( − ∞ ; − 4 ) №2. Решить неравество 6 x + 4 ≥ 3 ( x + 1 ) − 14. Решение: Раскрываем скобки, переносим иксы влево, числа вправо, приводим подобные слагаемые. 6 x + 4 ≥ 3 x + 3 − 14 6 x − 3 x ≥ 3 − 14 − 4 3 x ≥ − 15 | ÷ 3 Делим обе части неравенства на ( 3 ) – коэффициент, который стоит перед x . Так как 3 > 0, знак неравенства после деления меняться не будет. x ≥ − 15 3 ⇒ x ≥ − 5 Остается записать ответ (см. таблицу числовых промежутков). Особые случаи (в 14 задании ОГЭ 2019 они не встречались, но знать их полезно). №1. Решить неравенство 6 x − 1 ≤ 2 ( 3 x − 0,5 ). Решение: Раскрываем скобки, переносим иксы влево, числа вправо, приводим подобные слагаемые. 6 x − 6 x ≤ − 1 + 1 Получили верное неравенство, которое не зависит от переменной x . Возникает вопрос, какие значения может принимать переменная x , чтобы неравенство выполнялось? Любые! Какое бы значение мы ни взяли, оно все равно сократится и результат неравенства будет верным. Рассмотрим три варианта записи ответа. Ответ: x – любое число x ∈ ( − ∞ ; + ∞ ) x ∈ ℝ №2. Решить неравенство x + 3 ( 2 − 3 x ) > − 4 ( 2 x − 12 ). Решение: Раскрываем скобки, переносим иксы влево, числа вправо, приводим подобные слагаемые. x + 6 − 9 x > − 8 x + 48 − 8 x + 8 x > 48 − 6 Получили неверное равенство, которое не зависит от переменной x . Какие бы значения мы ни подставляли в исходное неравенство, результат окажется одним и тем же – неверное неравенство. Ни при каких значениях x исходное неравенство не станет верным. Данное неравенство не имеет решений. Запишем ответ. Квадратные неравенства Квадратные неравенства – это неравенства вида: a x 2 + b x + c > 0 a x 2 + b x + c ≥ 0 a x 2 + b x + c 0 a x 2 + b x + c ≤ 0 где a, b, c — некоторые числа, причем a ≠ 0, x — переменная. Существует универсальный метод решения неравенств степени выше первой (квадратных, кубических, биквадратных и т.д.) – метод интервалов. Если его один раз как следует осмыслить, то проблем с решением любых неравенств не возникнет. Для того, чтобы применять метод интервалов для решения квадратных неравенств, надо уметь хорошо решать квадратные уравнения (см. урок 4). Алгоритм решения квадратного неравенства методом интервалов Решить уравнение a x 2 + b x + c = 0 и найти корни x 1 и x 2 . Отметить на числовой прямой корни трехчлена. Если знак неравенства строгий > , , точки будут выколотые. Если знак неравенства нестрогий ≥ , ≤ , точки будут жирные (заштрихованный). Расставить знаки на интервалах. Для этого надо выбрать точку из любого промежутка (в примере взята точка A ) и подставить её значение в выражение a x 2 + b x + c вместо x . Если получилось положительное число, знак на интервале плюс. На остальных интервалах знаки будут чередоваться. Точки выколотые, если знак неравенства строгий. Точки жирные, если знак неравенства нестрогий. Если получилось отрицательное число, знак на интервале минус. На остальных интервалах знаки будут чередоваться. Точки выколотые, если знак неравенства строгий. Точки жирные, если знак неравенства нестрогий. Выбрать подходящие интервалы (или интервал). Если знак неравенства > или ≥ в ответ выбираем интервалы со знаком +. Если знак неравенства или ≤ в ответ выбираем интервалы со знаком -. Примеры решения квадратных неравенств: №1. Решить неравенство x 2 ≥ x + 12. Решение: Приводим неравенство к виду a x 2 + b x + c ≥ 0, а затем решаем уравнение a x 2 + b x + c = 0. a = 1, b = − 1, c = − 12 D = b 2 − 4 a c = ( − 1 ) 2 − 4 ⋅ 1 ⋅ ( − 12 ) = 1 + 48 = 49 D > 0 ⇒ будет два различных действительных корня x 1,2 = − b ± D 2 a = − ( − 1 ) ± 49 2 ⋅ 1 = 1 ± 7 2 = [ 1 + 7 2 = 8 2 = 4 1 − 7 2 = − 6 2 = − 3 Наносим точки на ось x . Так как знак неравенства нестрогий, точки будут жирными. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 6 . Подставляем эту точку в исходное выражение: x 2 − x − 1 = 6 2 − 6 − 1 = 29 > 0 Это значит, что знак на интервале, в котором лежит точка 6 будет +. Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный. В ответ пойдут два интервала. В математике для объединения нескольких интервалов используется знак объединения: ∪ . Точки -3 и 4 будут в квадратных скобках, так как они жирные. Ответ: x ∈ ( − ∞ ; − 3 ] ∪ [ 4 ; + ∞ ) №2. Решить неравенство − 3 x − 2 ≥ x 2 . Решение: Приводим неравенство к виду a x 2 + b x + c ≥ 0, а затем решаем уравнение a x 2 + b x + c = 0. a = − 1, b = − 3, c = − 2 D = b 2 − 4 a c = ( − 3 ) 2 − 4 ⋅ ( − 1 ) ⋅ ( − 2 ) = 9 − 8 = 1 D > 0 ⇒ будет два различных действительных корня x 1,2 = − b ± D 2 a = − ( − 3 ) ± 1 2 ⋅ ( − 1 ) = 3 ± 1 − 2 = [ 3 + 1 − 2 = 4 − 2 = − 2 3 − 1 − 2 = 2 − 2 = − 1 x 1 = − 2, x 2 = − 1 Наносим точки на ось x . Так как знак неравенства нестрогий, точки будут жирными. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 0 . Подставляем эту точку в исходное выражение: − x 2 − 3 x − 2 = − ( 0 ) 2 − 3 ⋅ 0 − 2 = − 2 0 Это значит, что знак на интервале, в котором лежит точка 0 будет − . Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный. Поскольку знак неравенства ≥ , выбираем в ответ интервал со знаком +. Точки -2 и -1 будут в квадратных скобках, так как они жирные. Ответ: x ∈ [ − 2 ; − 1 ] №3. Решить неравенство 4 x 2 + 3 x . Решение: Приводим неравенство к виду a x 2 + b x + c ≥ 0, а затем решаем уравнение a x 2 + b x + c = 0. a = − 1, b = − 3, c = 4 D = b 2 − 4 a c = ( − 3 ) 2 − 4 ⋅ ( − 1 ) ⋅ 4 = 9 + 16 = 25 D > 0 ⇒ будет два различных действительных корня x 1,2 = − b ± D 2 a = − ( − 3 ) ± 25 2 ⋅ ( − 1 ) = 3 ± 5 − 2 = [ 3 + 5 − 2 = 8 − 2 = − 4 3 − 5 − 2 = − 2 − 2 = 1 Наносим точки на ось x . Так как знак неравенства строгий, точки будут выколотыми. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 2 . Подставляем эту точку в исходное выражение: − x 2 − 3 x + 4 = − ( 2 ) 2 − 3 ⋅ 2 + 4 = − 6 0 Это значит, что знак на интервале, в котором лежит точка 2 , будет -. Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный. Поскольку знак неравенства , выбираем в ответ интервалы со знаком − . Точки -4 и 1 будут в круглых скобках, так как они выколотые. Ответ: x ∈ ( − ∞ ; − 4 ) ∪ ( 1 ; + ∞ ) №4. Решить неравенство x 2 − 5 x 6. Решение: Приводим неравенство к виду a x 2 + b x + c ≥ 0, а затем решаем уравнение a x 2 + b x + c = 0. a = 1, b = − 5, c = − 6 D = b 2 − 4 a c = ( − 5 ) 2 − 4 ⋅ 1 ⋅ ( − 6 ) = 25 + 25 = 49 D > 0 ⇒ будет два различных действительных корня x 1,2 = − b ± D 2 a = − ( − 5 ) ± 49 2 ⋅ 1 = 5 ± 7 2 = [ 5 + 7 2 = 12 2 = 6 5 − 7 2 = − 2 2 = − 1 Наносим точки на ось x . Так как знак неравенства строгий, точки будут выколотыми. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 10. Подставляем эту точку в исходное выражение: x 2 − 5 x − 6 = 10 2 − 5 ⋅ 10 − 6 = 100 − 50 − 6 = 44 > 0 Это значит, что знак на интервале, в котором лежит точка 10 будет +. Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный. Поскольку знак неравенства , выбираем в ответ интервал со знаком -. Точки -1 и 6 будут в круглых скобках, так как они выколотые Ответ: x ∈ ( − 1 ; 6 ) №5. Решить неравенство x 2 4. Решение: Переносим 4 в левую часть, раскладываем выражение на множители по ФСУ и находим корни уравнения. ( x − 2 ) ( x + 2 ) = 0 ⇔ [ x − 2 = 0 x + 2 = 0 [ x = 2 x = − 2 Наносим точки на ось x . Так как знак неравенства строгий, точки будут выколотыми. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 3 . Подставляем эту точку в исходное выражение: x 2 − 4 = 3 2 − 4 = 9 − 4 = 5 > 0 Это значит, что знак на интервале, в котором лежит точка 3 будет +. Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный. Поскольку знак неравенства , выбираем в ответ интервал со знаком − . Точки -2 и 2 будут в круглых скобках, так как они выколотые. Ответ: x ∈ ( − 2 ; 2 ) №6. Решить неравенство x 2 + x ≥ 0. Решение: Выносим общий множитель за скобку, находим корни уравнения x 2 + x = 0. x ( x + 1 ) = 0 ⇔ [ x = 0 x + 1 = 0 [ x = 0 x = − 1 Наносим точки на ось x . Так как знак неравенства нестрогий, точки будут жирными. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 1 . Подставляем эту точку в исходное выражение: x 2 + x = 1 2 + 1 = 2 > 0 Это значит, что знак на интервале, в котором лежит точка 1 будет +. Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный. Поскольку знак неравенства ≥ , выбираем в ответ интервалы со знаком +. В ответ пойдут два интервала. Точки -1 и 0 будут в квадратных скобках, так как они жирные. Ответ: x ∈ ( − ∞ ; − 1 ] ∪ [ 0 ; + ∞ ) Вот мы и познакомились с методом интервалов. Он нам еще пригодится при решении дробно рациональных неравенств, речь о которых пойдёт ниже. Дробно рациональные неравенства Дробно рациональное неравенство – это неравенство, в котором есть дробь, в знаменателе которой стоит переменная, т.е. неравенство одного из следующих видов: f ( x ) g ( x ) 0 f ( x ) g ( x ) ≤ 0 f ( x ) g ( x ) > 0 f ( x ) g ( x ) ≥ 0 Дробно рациональное неравенство не обязательно сразу выглядит так. Иногда, для приведения его к такому виду, приходится потрудиться (перенести слагаемые в левую часть, привести к общему знаменателю). Примеры дробно рациональных неравенств: x − 1 x + 3 0 3 ( x + 8 ) ≤ 5 x 2 − 1 x > 0 x + 20 x ≥ x + 3 Как же решать эти дробно рациональные неравенства? Да всё при помощи того же всемогущего метода интервалов. Алгоритм решения дробно рациональных неравенств: Привести неравенство к одному из следующих видов (в зависимости от знака в исходном неравенстве): f ( x ) g ( x ) 0 f ( x ) g ( x ) ≤ 0 f ( x ) g ( x ) > 0 f ( x ) g ( x ) ≥ 0 Приравнять числитель дроби к нулю f ( x ) = 0. Найти нули числителя . Приравнять знаменатель дроби к нулю g ( x ) = 0. Найти нули знаменателя . В этом пункте алгоритма мы будем делать всё то, что нам запрещали делать все 9 лет обучения в школе – приравнивать знаменатель дроби к нулю. Чтобы как-то оправдать свои буйные действия, полученные точки при нанесении на ось x будем всегда рисовать выколотыми, вне зависимости от того, какой знак неравенства. Нанести нули числителя и нули знаменателя на ось x . Вне зависимости от знака неравенства при нанесении на ось x нули знаменателя всегда выколотые . Если знак неравенства строгий , при нанесении на ось x нули числителя выколотые . Если знак неравенства нестрогий , при нанесении на ось x нули числителя жирные . Расставить знаки на интервалах. Выбрать подходящие интервалы и записать ответ. Примеры решения дробно рациональных неравенств: №1. Решить неравенство x − 1 x + 3 > 0. Решение: Будем решать данное неравенство в соответствии с алгоритмом. Первый шаг алгоритма уже выполнен. Неравенство приведено к виду f ( x ) g ( x ) > 0. Приравниваем числитель к нулю f ( x ) = 0. x = 1 — это ноль числителя . Поскольку знак неравенства строгий, ноль числителя при нанесени на ось x будет выколотым. Запомним это. Приравниваем знаменатель к нулю g ( x ) = 0. x = − 3 — это ноль знаменателя . При нанесении на ось x точка будет всегда выколотой (вне зависимости от знака неравенства) . Наносим нули числителя и нули знаменателя на ось x . При нанесении нулей числителя обращаем внимание на знак неравенства. В данном случае знак неравенства строгий, значит нули числителя будут выколотыми. Ну а нули знаменателя выколоты всегда. Расставляем знаки на интервалах. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 2 . Подставляем эту точку в исходное выражение f ( x ) g ( x ) : x − 1 x + 3 = 2 − 1 2 + 3 = 1 5 > 0, Это значит, что знак на интервале, в котором лежит точка 2 будет +. Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный. Выбираем подходящие интервалы и записываем ответ. Поскольку знак неравенства > , выбираем в ответ интервалы со знаком +. В ответ пойдут два интервала. Точки -3 и 1 будут в круглых скобках, так как обе они выколотые. Ответ: x ∈ ( − ∞ ; − 3 ) ∪ ( 1 ; + ∞ ) №2. Решить неравенство 3 ( x + 8 ) ≤ 5. Решение: Будем решать данное неравенство в соответствии с алгоритмом. Привести неравенство к виду f ( x ) g ( x ) ≤ 0. 3 ( x + 8 ) − 5 x + 8 ≤ 0 3 x + 8 − 5 ( x + 8 ) x + 8 ≤ 0 3 − 5 ( x + 8 ) x + 8 ≤ 0 3 − 5 x − 40 x + 8 ≤ 0 − 5 x − 37 x + 8 ≤ 0 Приравнять числитель к нулю f ( x ) = 0. x = − 37 5 = − 37 5 = − 7,4 x = − 7,4 — ноль числителя . Поскольку знак неравенства нестрогий, при нанесении этой точки на ось x точка будет жирной. Приравнять знаменатель к нулю g ( x ) = 0. x = − 8 — это ноль знаменателя . При нанесении на ось x , точка будет всегда выколотой (вне зависимости от знака неравенства). Наносим нули числителя и нули знаменателя на ось x . При нанесении нулей числителя обращаем внимание на знак неравенства. В данному случае знак неравенства нестрогий, значит нули числителя будут жирными. Ну а нули знаменателя выколоты всегда. Расставляем знаки на интервалах. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 0 . Подставляем эту точку в исходное выражение f ( x ) g ( x ) : − 5 x − 37 x + 8 = − 5 ⋅ 0 − 37 0 + 8 = − 37 8 0 Это значит, что знак на интервале, в котором лежит точка 0 будет -. Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный. Выбираем подходящие интервалы и записываем ответ. Поскольку знак неравенства ≤ , выбираем в ответ интервалы со знаком -. В ответ пойдут два интервала. Точка -8 будет в круглой скобке, так как она выколотая, точка -7,4 будет в квадратных скобках, так как она жирная. Ответ: x ∈ ( − ∞ ; − 8 ) ∪ [ − 7,4 ; + ∞ ) №3. Решить неравенство x 2 − 1 x > 0. Решение: Будем решать данное неравенство в соответствии с алгоритмом. Первый шаг алгоритма уже выполнен. Неравенство приведено к виду f ( x ) g ( x ) > 0. Приравнять числитель к нулю f ( x ) = 0. ( x − 1 ) ( x + 1 ) = 0 ⇒ [ x − 1 = 0 x + 1 = 0 [ x = 1 x = − 1 x 1 = 1, x 2 = − 1 — нули числителя . Поскольку знак неравенства строгий, при нанесении этих точек на ось x точки будут выколотыми. Приравнять знаменатель к нулю g ( x ) = 0. x = 0 — это ноль знаменателя . При нанесении на ось x , точка будет всегда выколотой (вне зависимости от знака неравенства). Наносим нули числителя и нули знаменателя на ось x . При нанесении нулей числителя обращаем внимание на знак неравенства. В данному случае знак неравенства строгий, значит нули числителя будут выколотыми. Ну а нули знаменателя и так выколоты всегда. Расставляем знаки на интервалах. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 2 . Подставляем эту точку в исходное выражение f ( x ) g ( x ) : x 2 − 1 x = 2 2 − 1 2 = 4 − 1 2 = 3 2 > 0, Это значит, что знак на интервале, в котором лежит точка 2, будет +. Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный. Выбираем подходящие интервалы и записываем ответ. Поскольку знак неравенства > , выбираем в ответ интервалы со знаком +. В ответ пойдут два интервала. Все точки будут в круглых скобках, так как они выколотые. Ответ: x ∈ ( − 1 ; 0 ) ∪ ( 1 ; + ∞ ) Системы неравенств Системой неравенств называют два неравенства с одной неизвестной, которые объединены в общую систему фигурной скобкой. Пример системы неравенств: Алгоритм решения системы неравенств Решить первое неравенство системы, изобразить его графически на оси x . Решить второе неравенство системы, изобразить его графически на оси x . Нанести решения первого и второго неравенств на ось x . Выбрать в ответ те участки, в которых решение первого и второго неравенств пересекаются. Записать ответ. Примеры решений систем неравенств: №1. Решить систему неравенств < 2 x − 3 ≤ 5 7 − 3 x ≤ 1 Решение: Будем решать данную систему неравенств в соответствии с алгоритмом. Решаем первое неравенство системы. 2 x ≤ 8 | ÷ 2 , поскольку 2 > 0, знак неравенства после деления сохраняется. Точка 4 на графике жирная, так как знак неравенства нестрогий. Решаем второе неравенство системы. − 3 x ≤ − 6 | ÷ ( − 3 ), поскольку − 3 0, знак неравенства после деления меняется на противоположный. Графическая интерпретация решения: Точка 2 на графике жирная, так как знак неравенства нестрогий. Наносим оба решения на ось x . Выбираем подходящие участки и записываем ответ. Пересечение решений наблюдается на отрезке от 2 до 4 . Точки 2 и 4 в ответе буду в квадратных скобках, так как обе они жирные. №2. Решить систему неравенств < 2 x − 1 ≤ 5 1 − 3 x − 2 Решение: Будем решать данную систему неравенств в соответствии с алгоритмом. Решаем первое неравенство системы. 2 x ≤ 6 | ÷ 2 , поскольку 2 > 0, знак неравенства после деления сохраняется. Точка 3 на графике жирная, так как знак неравенства нестрогий. Решаем второе неравенство системы. 3 x − 3 | ÷ 3 , поскольку 3 > 0, знак неравенства после деления сохраняется. Графическая интерпретация решения: Точка -1 на графике выколотая, так как знак неравенства строгий. Наносим оба решения на ось x . Выбираем подходящие участки и записываем ответ. Пересечение решений наблюдается на самом левом участке. Точка -1 будет в ответе в круглых скобках, так как она выколотая. Ответ: x ∈ ( − ∞ ; − 1 ) №3. Решить систему неравенств 5 − x Решение: Будем решать данную систему неравенств в соответствии с алгоритмом. Решаем первое неравенство системы. Графическая интерпретация решения: Решаем второе неравенство системы 2 x > 12 | ÷ 2 , поскольку 2 > 0, знак неравенства после деления сохраняется. Графическая интерпретация решения: Наносим оба решения на ось x . Выбираем подходящие участки и записываем ответ. Пересечений решений не наблюдается. Значит у данной системы неравенств нет решений. №4. Решить систему неравенств 0 2 x + 3 ≤ x 2 Решение: Будем решать данную систему неравенств в соответствии с алгоритмом. Решаем первое неравенство системы. Графическая интерпретация решения первого неравенства: Решаем второе неравенство системы Решаем методом интервалов. a = − 1, b = 2, c = 3 D = b 2 − 4 a c = 2 2 − 4 ⋅ ( − 1 ) ⋅ 3 = 4 + 12 = 16 D > 0 — два различных действительных корня. x 1,2 = − b ± D 2 a = − 2 ± 16 2 ⋅ ( − 1 ) = − 2 ± 4 − 2 = [ − 2 − 4 − 2 = − 6 − 2 = 3 − 2 + 4 − 2 = 2 − 2 = − 1 Наносим точки на ось x и расставляем знаки на интервалах. Поскольку знак неравенства нестрогий, обе точки будут заштрихованными. Графическая интерпретация решения второго неравенства: Наносим оба решения на ось x . Выбираем подходящие участки и записываем ответ. Пересечение решений наблюдается в двух интервалах. Для того, чтобы в ответе объединить два интервала, используется знак объединения ∪ . Точка -4 будет в круглой скобке, так как она выколотая, а точки -1 и 3 в квадратных, так как они жирные. Видео:ЛИНЕЙНЫЕ НЕРАВЕНСТВА - Как решать линейные неравенства // Подготовка к ЕГЭ по МатематикеСкачать Решение задач по математике онлайн

Отсюда ясно, что:
если ( x in (-infty;-2) ), то f(x) 0;
если ( x in (3;5) ), то f(x) 0.

Мы видим, что в каждом из промежутков ( (-infty; -2), ; (-2; 3), ; (3; 5), ; (5; +infty) ) функция сохраняет знак, а при переходе через точки -2, 3 и 5 ее знак изменяется.

Вообще пусть функция задана формулой
f(x) = (x-x₁)(x-x₂) . (x-x_n),
где x–переменная, а x₁, x₂, . x_n – не равные друг другу числа. Числа x₁, x₂, . x_n являются нулями функции. В каждом из промежутков, на которые область определения разбивается нулями функции, знак функции сохраняется, а при переходе через нуль ее знак изменяется.

Выбираем те промежутки, на которых функция меньше нуля и записываем ответ.

Ответ:
( x in left( -4; ; 0 right) cup left( 0,5; ; +infty right) )
или
( -4 0,5 )

Наносим на числовую ось нули и точки разрыва функции:

Выбираем те промежутки, на которых функция меньше или равна нулю и записываем ответ.

Ответ:
( x in left( -infty; ; 1 right) cup left[ 4; ; +infty right) )
или
( x

Видео:ЛИНЕЙНЫЕ УРАВНЕНИЯ - Как решать линейные уравнения // Подготовка к ЕГЭ по МатематикеСкачать

«Решение линейных и квадратных неравенств с одной переменной»

• Повторить понятие неравенства первой и второй степени с одной переменной, дать определение.
• Повторить алгоритмы решения неравенств на основе свойств линейной квадратичной функции.
• Сформировать навыки и умения решать неравенства данных видов.

Просмотр содержимого документа
«доп материал»

Алгоритмы решения неравенств:

Раскрыть скобки, имеющиеся в обеих частях уравнения, упростить выражения;

Перенести члены, содержащие неизвестную

величину в левую часть, а члены , не содержащие неизвестную величину, -в правую;

Разделить обе части неравенства на коэффициент при неизвестном, если он не равен нулю , при этом важно помнить, что знак неравенства сохраняется, если делим на положительное число, и знак неравенства меняется на противоположный, если делим на отрицательное число

Записать ответ в виде промежутка или неравенства

Определить направление ветвей функции

Найти корни квадратного уравнения

ax 2 + bx + c =0, которые являются точками пересечения с осью Ох

Отметить на координатной прямой найденные корни и схематически изобразить параболу

Определить, на каких промежутках оси х ординаты графика положительны (отрицательны)

Записать ответ в виде промежутка или неравенства.

Алгоритмы решения неравенств:

Раскрыть скобки, имеющиеся в обеих частях уравнения, упростить выражения;

Перенести члены, содержащие неизвестную

величину в левую часть, а члены , не содержащие неизвестную величину, -в правую;

Разделить обе части неравенства на коэффициент при неизвестном, если он не равен нулю , при этом важно помнить, что знак неравенства сохраняется, если делим на положительное число, и знак неравенства меняется на противоположный, если делим на отрицательное число

Записать ответ в виде промежутка или неравенства

Определить направление ветвей функции

Найти корни квадратного уравнения

ax 2 + bx + c =0, которые являются точками пересечения с осью Ох

Отметить на координатной прямой найденные корни и схематически изобразить параболу

Определить, на каких промежутках оси х ординаты графика положительны (отрицательны)

Записать ответ в виде промежутка или неравенства.

Просмотр содержимого документа
«открытый урок»

Муниципальное Бюджетное Образование

Основной Общеобразовательной Школы № 31

«Решение линейных и квадратных

неравенств с одной переменной»

Лапшина Анна Владимировна

2012-2013 учебный год

«С тех пор как существует мирозданье,
Такого нет, кто б не нуждался в знанье.
Какой мы ни возьмем язык и век,
Всегда стремится к знанью человек»

Урок закрепления знаний (умений и навыков) по пройденному материалу.

Повторить понятие неравенства первой и второй степени с одной переменной, дать определение.

Повторить алгоритмы решения неравенств на основе свойств линейной квадратичной функции.

Сформировать навыки и умения решать неравенства данных видов.

Выработать умения анализировать, выделять главное, сравнивать, обобщать.

Формировать графическую и функциональную культуру учащихся.

Показать взаимосвязь математики с окружающей действительностью.

Формировать навыки общения, умения работать индивидуально и в парах.

Раздаточный материал (карточки с алгоритмами, карточки с заданиями, таблички с графической интерпретацией)

Плакаты с алгоритмами решения неравенств

Учебник 9 класса (А.Г. Мордкович, Л.А. Александрова, Т.Н. Мишустина)

Рабочие тетради учащихся

Сообщение темы и цели урока

Актуализация знаний в виде устной работы по заданиям на доске

Составление алгоритма решения линейных и квадратных неравенств

Работа у доски, развитие устной речи.

Решение заданий из учебника по алгоритмам.

Самостоятельная работа по табличкам с графической интерпретацией

Подведение итогов урока.

Запись домашней работы в дневники.

Ι. Организационный момент.

Ни один школьный экзамен не обходится без задания с неравенствами различных видов. Но практически все неравенства сводятся к решению двух видов:

— Какие виды неравенств вы знаете? (это линейные и квадратные неравенства).

— Понятие «неравенство» какими знаками определяется? (знаком больше и меньше)

Понятия « больше», « меньше» наряду с понятием равенства возникли в связи со счетом предметов и необходимостью сравнивать различные величины. Понятием неравенства пользовались уже древние греки. Архимед, занимаясь вычислением длины окружности, указал границы числа П. Однако, все рассуждения проводили словесно, опираясь в большинстве случаев на геометрическую терминологию. Современные знаки неравенств появились лишь в ХVII – XVIII вв. Знаки ,

А находит ли применение эти неравенства в окружающем нас мире или может это просто прихоть математиков?! Наверно нет! Ведь всякое явление можно описать с помощью функции, а умения решать неравенства позволяют ответить на вопрос, при каких значениях аргумента эта функция положительна, а при каких отрицательна.

Каскады падающей воды — фонтаны украшают многие города, развлекательные центры, дома. А при чем здесь неравенства? Чтобы ответить на этот вопрос нужно вспомнить, кукую функцию описывают капли воды из фонтана?

Итак, сегодня на уроке мы с вами закрепим наши знания и умения в решении линейных и квадратных неравенствах.

Какое неравенство называется линейным?

Что значит решить неравенство?

Какие правила применяются для решения линейного неравенства? (изменение знака неравенства и замена равносильным неравенством)

а) х -2; г) х ≤4; д) х ж) х

2)Укажите наибольшее целое число, принадлежащее промежутку:

а) (-8; 8) ; б) (-14; -1); в) [-6; 2]; г) [-1,5; 1,5]

а) 7; б) -2; в) 2; г) 1;

Какое неравенство называется квадратным неравенством?

Как найти корни квадратного трехчлена?

Что является графиком квадратичной функции?

Как располагается график квадратичной функции в зависимости от а и от числа корней уравнения ax 2 + bx + c =0;

Как определить промежуток знакопостоянства функции.

Каким методом решаются неравенства?

3) Назовите число корней уравнения ax 2 + bx + c =0 и знак коэффициента а,если график соответствующей квадратичной функции расположен следующим образом::

а) 2 корня, а›0; б) коней нет, а›0; в) 2 корня, а‹0;

г) коней нет, а‹0; д) 1 корень, а›0; е) 1 корень, а‹0;

4) Найдите корни квадратного трехчлена:

а) Д= 49, х1= 3, х2= -4; б) Д=0, х=0,5

Итак, мы повторили необходимый материал. С какими трудностями вы встретились при выполнении данных работ? Некоторые обнаружили у себя слабые места, но разобрались в своих ошибках, и я надеюсь, что больше эти ошибки они не совершат. (Подводится итог этапа актуализации).

ΙΙΙ. Закрепление пройденного материала.

Давайте с вами сформулируем алгоритмы решения линейных и квадратных неравенств и разберем примеры пошаговых решений двух неравенств:

Линейные неравенства Квадратные неравенства

Раскрыть скобки, имеющиеся в обеих частях уравнения, упростить выражения;

Перенести члены, содержащие неизвестную

величину в левую часть, а члены , не содержащие неизвестную величину, -в правую;

Разделить обе части неравенства на коэффициент при неизвестном, если он не равен нулю , при этом важно помнить, что знак неравенства сохраняется, если делим на положительное число, и знак неравенства меняется на противоположный, если делим на отрицательное число

Записать ответ в виде промежутка или неравенства

Определить направление ветвей функции

Найти корни квадратного уравнения

ax 2 + bx + c =0, которые являются точками пересечения с осью Ох

Отметить на координатной прямой найденные корни и схематически изобразить параболу

Определить, на каких промежутках оси х ординаты графика положительны (отрицательны)

Записать ответ в виде промежутка или неравенства.

На каждую парту раздаются карточки с алгоритмом решения неравенств.

К доске вызываются 2 ученика, и каждый решает своё неравенство, все остальные у себя в тетради.

5( х -1 )+8 ≤ 1 — 3( х + 2)

-1 х

Развитие устной речи

После решения примеров на доске классу предлагается задавать вопросы учащимся, которые решали неравенства. Ученик должен дать полный развернутый ответ, в случае не ответа, задаваемый сам должен ответить на поставленный вопрос. Оценивается и решающий и задающий вопрос.

В классе где-то спрятаны карточки с правильными и неправильными ответами решения этих неравенств, найдите их.

IV . Применение знаний, формирование умений и навыков.

Учебник: № 2.11 (а,б); № 2.15 (а,в); № 2.30 (а)

При наличии времени решить № 2.34

На каждой парте лежат карточки с заданиями. Учащиеся выполняют задания, а затем обмениваются карточками и проверяют друг друга, выставляя объективную оценку. Ответы видят на доске.

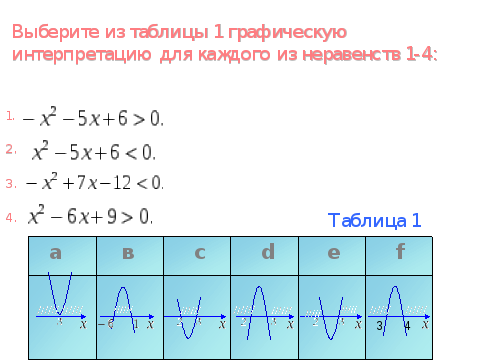
Ответ: таблица 2 – в; таблица 3 — а

Видео:КВАДРАТНЫЕ НЕРАВЕНСТВА ПОНЯТНЫМ ЯЗЫКОМСкачать

Линейные неравенства, примеры, решения

После получения начальных сведений о неравенствах с переменными, переходим к вопросу их решения. Разберем решение линейных неравенств с одной переменной и все методы для их разрешения с алгоритмами и примерами. Будут рассмотрены только линейные уравнения с одной переменной.

Видео:Урок по теме РЕШЕНИЕ НЕРАВЕНСТВ С ОДНОЙ ПЕРЕМЕННОЙСкачать

Что такое линейное неравенство?

В начале необходимо определить линейное уравнение и выяснить его стандартный вид и чем оно будет отличаться от других. Из школьного курса имеем, что у неравенств нет принципиального различия, поэтому необходимо использовать несколько определений.

Линейное неравенство с одной переменной x – это неравенство вида a · x + b > 0 , когда вместо > используется любой знак неравенства , ≤ , ≥ , а и b являются действительными числами, где a ≠ 0 .

Неравенства a · x c или a · x > c , с x являющимся переменной, а a и c некоторыми числами, называют линейными неравенствами с одной переменной.

Так как ничего не сказано за то, может ли коэффициент быть равным 0 , тогда строгое неравенство вида 0 · x > c и 0 · x c может быть записано в виде нестрогого, а именно, a · x ≤ c , a · x ≥ c . Такое уравнение считается линейным.

Их различия заключаются в:

• форме записи a · x + b > 0 в первом, и a · x > c – во втором;
• допустимости равенства нулю коэффициента a , a ≠ 0 — в первом, и a = 0 — во втором.

Считается, что неравенства a · x + b > 0 и a · x > c равносильные, потому как получены переносом слагаемого из одной части в другую. Решение неравенства 0 · x + 5 > 0 приведет к тому, что его необходимо будет решить, причем случай а = 0 не подойдет.

Считается, что линейными неравенствами в одной переменной x считаются неравенства вида a · x + b 0 , a · x + b > 0 , a · x + b ≤ 0 и a · x + b ≥ 0 , где a и b являются действительными числами. Вместо x может быть обычное число.

Исходя из правила, имеем, что 4 · x − 1 > 0 , 0 · z + 2 , 3 ≤ 0 , — 2 3 · x — 2 0 являются примерами линейных неравенств. А неравенства такого плана, как 5 · x > 7 , − 0 , 5 · y ≤ − 1 , 2 называют сводящимися к линейному.

Видео:Как решать неравенства? Математика 10 класс | TutorOnlineСкачать

Как решить линейное неравенство

Основным способом решения таких неравенств сводится к равносильным преобразованиям для того, чтобы найти элементарные неравенства x p ( ≤ , > , ≥ ) , p являющееся некоторым числом, при a ≠ 0 , а вида a p ( ≤ , > , ≥ ) при а = 0 .

Для решения неравенства с одной переменной, можно применять метода интервалов или изображать графически. Любой из них можно применять обособленно.

Видео:Линейное неравенство с одной переменной. 6 класс.Скачать

Используя равносильные преобразования

Чтобы решить линейное неравенство вида a · x + b 0 ( ≤ , > , ≥ ) , необходимо применить равносильные преобразования неравенства. Коэффициент может быть равен или не равен нулю. Рассмотрим оба случая. Для выяснения необходимо придерживаться схемы, состоящей из 3 пунктов: суть процесса, алгоритм, само решение.

Алгоритм решение линейного неравенства a · x + b 0 ( ≤ , > , ≥ ) при a ≠ 0

• число b будет перенесено в правую часть неравенства с противоположным знаком, что позволит прийти к равносильному a · x − b ( ≤ , > , ≥ ) ;
• будет производиться деление обеих частей неравенства на число не равное 0 . Причем , когда a является положительным, то знак остается, когда a – отрицательное, меняется на противоположный.

Рассмотрим применение данного алгоритма на решении примеров.

Решить неравенство вида 3 · x + 12 ≤ 0 .

Данное линейное неравенство имеет a = 3 и b = 12 . Значит, коэффициент a при x не равен нулю. Применим выше сказанные алгоритмы, решим.

Необходимо перенести слагаемое 12 в другую часть неравенства с изменением знака перед ним. Тогда получаем неравенство вида 3 · x ≤ − 12 . Необходимо произвести деление обеих частей на 3 . Знак не поменяется, так как 3 является положительным числом. Получаем, что ( 3 · x ) : 3 ≤ ( − 12 ) : 3 , что даст результат x ≤ − 4 .

Неравенство вида x ≤ − 4 является равносильным. То есть решение для 3 · x + 12 ≤ 0 – это любое действительное число, которое меньше или равно 4 . Ответ записывается в виде неравенства x ≤ − 4 , или числового промежутка вида ( − ∞ , − 4 ] .

Весь выше прописанный алгоритм записывается так:

3 · x + 12 ≤ 0 ; 3 · x ≤ − 12 ; x ≤ − 4 .

Ответ: x ≤ − 4 или ( − ∞ , − 4 ] .

Указать все имеющиеся решения неравенства − 2 , 7 · z > 0 .

Из условия видим, что коэффициент a при z равняется — 2 , 7 , а b в явном виде отсутствует или равняется нулю. Первый шаг алгоритма можно не использовать, а сразу переходить ко второму.

Производим деление обеих частей уравнения на число — 2 , 7 . Так как число отрицательное, необходимо поменять знак неравенства на противоположный. То есть получаем, что ( − 2 , 7 · z ) : ( − 2 , 7 ) 0 : ( − 2 , 7 ) , и дальше z 0 .

Весь алгоритм запишем в краткой форме:

− 2 , 7 · z > 0 ; z 0 .

Ответ: z 0 или ( − ∞ , 0 ) .

Решить неравенство — 5 · x — 15 22 ≤ 0 .

По условию видим, что необходимо решить неравенство с коэффициентом a при переменной x , которое равняется — 5 , с коэффициентом b , которому соответствует дробь — 15 22 . Решать неравенство необходимо, следуя алгоритму, то есть: перенести — 15 22 в другую часть с противоположным знаком, разделить обе части на — 5 , изменить знак неравенства:

— 5 · x ≤ 15 22 ; — 5 · x : — 5 ≥ 15 22 : — 5 x ≥ — 3 22

При последнем переходе для правой части используется правило деления числе с разными знаками 15 22 : — 5 = — 15 22 : 5 , после чего выполняем деление обыкновенной дроби на натурально число — 15 22 : 5 = — 15 22 · 1 5 = — 15 · 1 22 · 5 = — 3 22 .

Ответ: x ≥ — 3 22 и [ — 3 22 + ∞ ) .

Рассмотрим случай, когда а = 0 . Линейное выражение вида a · x + b 0 является неравенством 0 · x + b 0 , где на рассмотрение берется неравенство вида b 0 , после чего выясняется, оно верное или нет.

Все основывается на определении решения неравенства. При любом значении x получаем числовое неравенство вида b 0 , потому что при подстановке любого t вместо переменной x , тогда получаем 0 · t + b 0 , где b 0 . В случае, если оно верно, то для его решения подходит любое значение. Когда b 0 неверно, тогда линейное уравнение не имеет решений, потому как не имеется ни одного значения переменной, которое привело бы верному числовому равенству.

Все суждения рассмотрим в виде алгоритма решения линейных неравенств 0 · x + b 0 ( ≤ , > , ≥ ) :

Числовое неравенство вида b 0 ( ≤ , > , ≥ ) верно, тогда исходное неравенство имеет решение при любом значении, а неверно тогда, когда исходное неравенство не имеет решений.

Решить неравенство 0 · x + 7 > 0 .

Данное линейное неравенство 0 · x + 7 > 0 может принимать любое значение x . Тогда получим неравенство вида 7 > 0 . Последнее неравенство считается верным, значит любое число может быть его решением.

Найти решение неравенства 0 · x − 12 , 7 ≥ 0 .

При подстановке переменной x любого числа получим, что неравенство получит вид − 12 , 7 ≥ 0 . Оно является неверным. То есть 0 · x − 12 , 7 ≥ 0 не имеет решений.

Ответ: решений нет.

Рассмотрим решение линейных неравенств , где оба коэффициента равняется нулю.

Определить не имеющее решение неравенство из 0 · x + 0 > 0 и 0 · x + 0 ≥ 0 .

При подстановке любого числа вместо x получим два неравенства вида 0 > 0 и 0 ≥ 0 . Первое является неверным. Значит, 0 · x + 0 > 0 не имеет решений, а 0 · x + 0 ≥ 0 имеет бесконечное количество решений, то есть любое число.

Ответ: неравенство 0 · x + 0 > 0 не имеет решений, а 0 · x + 0 ≥ 0 имеет решения.

Видео:Линейные неравенства. Решение линейных неравенств с одной переменной. Числовые промежутки. Алгебра 9Скачать

Методом интервалов

Данный метод рассматривается в школьном курсе математики. Метод интервалов способен разрешать различные виды неравенств, также и линейные.

Метод интервалов применяется для линейных неравенств при значении коэффициента x не равному 0 . Иначе придется вычислять при помощи другого метода.

Метод интервалов – это:

• введение функции y = a · x + b ;
• поиск нулей для разбивания области определения на промежутки;
• определение знаков для понятия их на промежутках.

Соберем алгоритм для решения линейных уравнений a · x + b 0 ( ≤ , > , ≥ ) при a ≠ 0 с помощью метода интервалов:

• нахождение нулей функции y = a · x + b , чтобы решить уравнение вида a · x + b = 0 . Если a ≠ 0 , тогда решением будет единственный корень, который примет обозначение х 0 ;
• построение координатной прямой с изображением точки с координатой х 0 , при строгом неравенстве точка обозначается выколотой, при нестрогом – закрашенной;
• определение знаков функции y = a · x + b на промежутках, для этого необходимо находить значения функции в точках на промежутке;
• решение неравенства со знаками > или ≥ на координатной прямой добавляется штриховка над положительным промежутком, или ≤ над отрицательным промежутком.

Рассмотрим несколько примеров решения линейного неравенства при помощи метода интервалов.

Решить неравенство − 3 · x + 12 > 0 .

Из алгоритма следует, что для начала нужно найти корень уравнения − 3 · x + 12 = 0 . Получаем, что − 3 · x = − 12 , x = 4 . Необходимо изобразить координатную прямую, где отмечаем точку 4 . Она будет выколотой, так как неравенство является строгим. Рассмотрим чертеж, приведенный ниже.

Нужно определить знаки на промежутках. Чтобы определить его на промежутке ( − ∞ , 4 ) , необходимо произвести вычисление функции y = − 3 · x + 12 при х = 3 . Отсюда получим, что − 3 · 3 + 12 = 3 > 0 . Знак на промежутке является положительным.

Определяем знак из промежутка ( 4 , + ∞ ) , тогда подставляем значение х = 5 . Имеем, что − 3 · 5 + 12 = − 3 0 . Знак на промежутке является отрицательным. Изобразим на числовой прямой, приведенной ниже.

Мы выполняем решение неравенства со знаком > , причем штриховка выполняется над положительным промежутком. Рассмотрим чертеж, приведенный ниже.

Из чертежа видно, что искомое решение имеет вид ( − ∞ , 4 ) или x 4 .

Ответ: ( − ∞ , 4 ) или x 4 .

Видео:Неравенства с двумя переменными. 9 класс.Скачать

Графическим способом

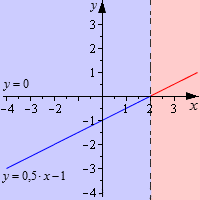
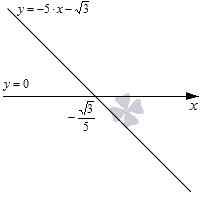
Чтобы понять, как изображать графически, необходимо рассмотреть на примере 4 линейных неравенства: 0 , 5 · x − 1 0 , 0 , 5 · x − 1 ≤ 0 , 0 , 5 · x − 1 > 0 и 0 , 5 · x − 1 ≥ 0 . Их решениями будут значения x 2 , x ≤ 2 , x > 2 и x ≥ 2 . Для этого изобразим график линейной функции y = 0 , 5 · x − 1 , приведенный ниже.

• решением неравенства 0 , 5 · x − 1 0 считается промежуток, где график функции y = 0 , 5 · x − 1 располагается ниже О х ;
• решением 0 , 5 · x − 1 ≤ 0 считается промежуток, где функция y = 0 , 5 · x − 1 ниже О х или совпадает;
• решением 0 , 5 · x − 1 > 0 считается промежуток, гре функция располагается выше О х ;
• решением 0 , 5 · x − 1 ≥ 0 считается промежуток, где график выше О х или совпадает.

Смысл графического решения неравенств заключается в нахождении промежутков, которое необходимо изображать на графике. В данном случае получаем, что левая часть имеет y = a · x + b , а правая – y = 0 , причем совпадает с О х .

Видео:Линейное уравнение с одной переменной. 6 класс.Скачать

Алгоритм решения линейных неравенств графическим способом.

Построение графика функции y = a · x + b производится:

• во время решения неравенства a · x + b 0 определяется промежуток, где график изображен ниже О х ;
• во время решения неравенства a · x + b ≤ 0 определяется промежуток, где график изображается ниже оси О х или совпадает;
• во время решения неравенства a · x + b > 0 производится определение промежутка, где график изображается выше О х ;
• во время решения неравенства a · x + b ≥ 0 производится определение промежутка, где график находится выше О х или совпадает.

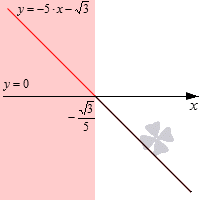
Решить неравенство — 5 · x — 3 > 0 при помощи графика.

Необходимо построить график линейной функции — 5 · x — 3 > 0 . Данная прямая является убывающей, потому как коэффициент при x является отрицательным. Для определения координат точки его пересечения с О х — 5 · x — 3 > 0 получим значение — 3 5 . Изобразим графически.

Решение неравенства со знаком > , тогда необходимо обратить внимание на промежуток выше О х . Выделим красным цветом необходимую часть плоскости и получим, что

Необходимый промежуток является частью О х красного цвета. Значит, открытый числовой луч — ∞ , — 3 5 будет решением неравенства. Если бы по условию имели нестрогое неравенство, тогда значение точки — 3 5 также являлось бы решением неравенства. И совпадало бы с О х .

Ответ: — ∞ , — 3 5 или x — 3 5 .

Графический способ решения используется, когда левая часть будет отвечать функции y = 0 · x + b , то есть y = b . Тогда прямая будет параллельна О х или совпадающей при b = 0 . Эти случаю показывают, что неравенство может не иметь решений, либо решением может быть любое число.

Определить из неравенств 0 · x + 7 = 0 , 0 · x + 0 ≥ 0 то, которое имеет хотя бы одно решение.

Представление y = 0 · x + 7 является y = 7 , тогда будет задана координатная плоскость с прямой, параллельной О х и находящейся выше О х . Значит, 0 · x + 7 = 0 решений не имеет, потому как нет промежутков.

График функции y = 0 · x + 0 , считается y = 0 , то есть прямая совпадает с О х . Значит, неравенство 0 · x + 0 ≥ 0 имеет множество решений.

Ответ: второе неравенство имеет решение при любом значении x .

Видео:Решение системы линейных неравенств с одной переменной. 6 класс.Скачать

Неравенства, сводящиеся к линейным

Решение неравенств можно свести к решению линейного уравнения, которые называют неравенствами, сводящимися к линейным.

Данные неравенства были рассмотрены в школьном курсе, так как они являлись частным случаем решения неравенств, что приводило к раскрытию скобок и приведению подобных слагаемых. Для примера рассмотрим, что 5 − 2 · x > 0 , 7 · ( x − 1 ) + 3 ≤ 4 · x − 2 + x , x — 3 5 — 2 · x + 1 > 2 7 · x .

Неравенства, приведенные выше, всегда приводятся к виду линейного уравнения. После чего раскрываются скобки и приводятся подобные слагаемые, переносятся из разных частей, меняя знак на противоположный.

При сведении неравенства 5 − 2 · x > 0 к линейному, представляем его таким образом, чтобы оно имело вид − 2 · x + 5 > 0 , а для приведения второго получаем, что 7 · ( x − 1 ) + 3 ≤ 4 · x − 2 + x . Необходимо раскрыть скобки, привести подобные слагаемые, перенести все слагаемые в левую часть и привести подобные слагаемые. Это выглядит таким образом:

7 · x − 7 + 3 ≤ 4 · x − 2 + x 7 · x − 4 ≤ 5 · x − 2 7 · x − 4 − 5 · x + 2 ≤ 0 2 · x − 2 ≤ 0

Это приводит решение к линейному неравенству.

Эти неравенства рассматриваются как линейные, так как имеют такой же принцип решения, после чего возможно приведение их к элементарным неравенствам.

Для решения такого вида неравенства такого вида необходимо свести его к линейному. Это следует делать таким образом:

• раскрыть скобки;
• слева собрать переменные, а справа числа;
• привести подобные слагаемые;
• разделить обе части на коэффициент при x .

Решить неравенство 5 · ( x + 3 ) + x ≤ 6 · ( x − 3 ) + 1 .

Производим раскрытие скобок, тогда получим неравенство вида 5 · x + 15 + x ≤ 6 · x − 18 + 1 . После приведения подобных слагаемых имеем, что 6 · x + 15 ≤ 6 · x − 17 . После перенесения слагаемых с левой в правую, получим, что 6 · x + 15 − 6 · x + 17 ≤ 0 . Отсюда имеет неравенство вида 32 ≤ 0 из полученного при вычислении 0 · x + 32 ≤ 0 . Видно, что неравенство неверное, значит, неравенство, данное по условию, не имеет решений.

Ответ: нет решений.

Стоит отметить, что имеется множество неравенств другого вида, которые могут сводится к линейному или неравенству вида, показанного выше. Например, 5 2 · x − 1 ≥ 1 является показательным уравнением, которое сводится к решению линейного вида 2 · x − 1 ≥ 0 . Эти случаи будут рассмотрены при решении неравенств данного вида.

🔍 Видео

Система уравнений VS Система неравенств. ОГЭ по математике №9, 13| Математика TutorOnlineСкачать

Алгебра 9. Урок 4 - Неравенства линейные - решение.Скачать

ОГЭ за одну минуту, математика задание 13, линейное неравенство.Скачать

Решение линейных неравенств с одной переменной. Числовые промежутки. Алгебра 9клСкачать