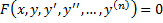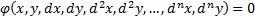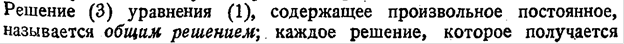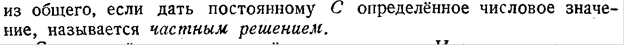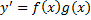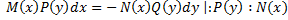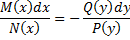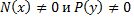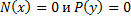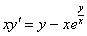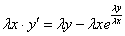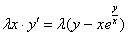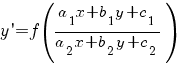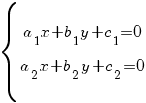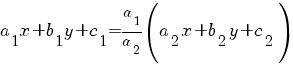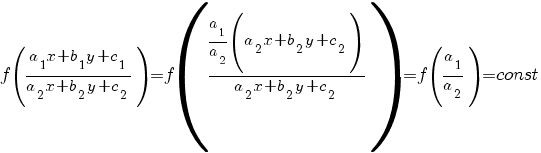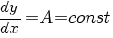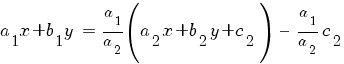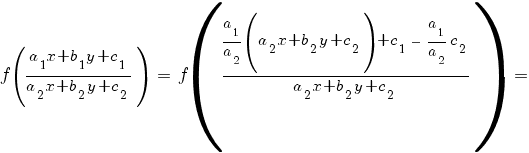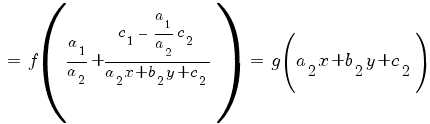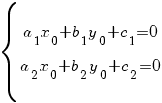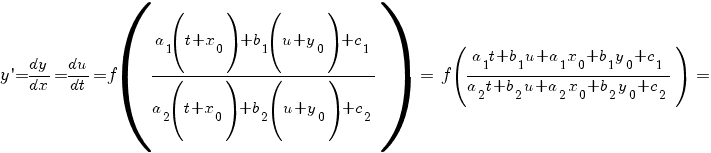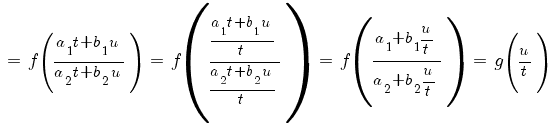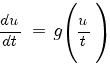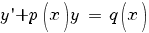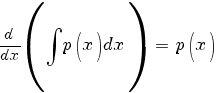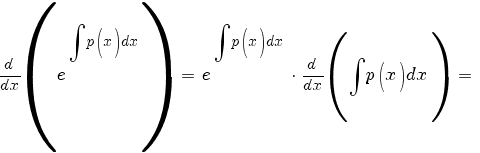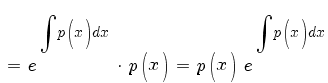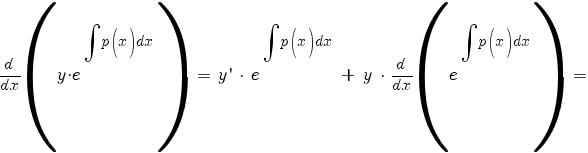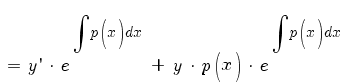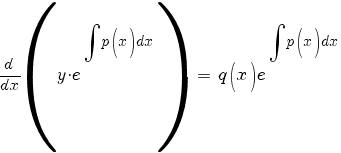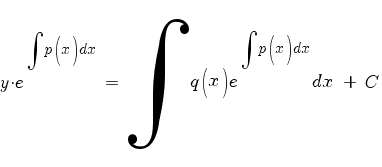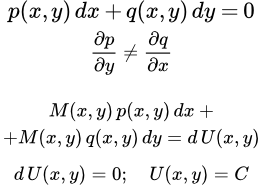Решение линейных дифференциальных уравнений метод интегрирующего множителя

Определение дифференциального уравнения. Понятие общего решения и частного решения.

Дифференциальное уравнение – уравнение, связывающее независимую переменную x и y, y’, y’’,…,y ( n)

Общий вид:

Решение ДУ – всякая функция 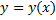, которая, при подстановке в ДУ, обращает ДУ в тождество.

При этом график функции 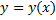называется интегральной кривой.

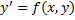
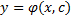
Общее решение уравнения это функция , удовлетворяющая следующим условиям:

1. C обращает в тождество

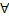
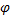
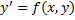
2. , удовлетворяет данным условиям, при этом — частное решение.

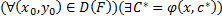
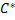
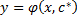
По Степанову:

Уравнения с разделяющимися переменными.

(*)

(*):

или при

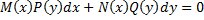
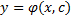
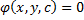
Затем проверим

Пусть 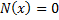при x=b, тогда x=b – частное решение.

Пусть 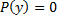при y=a, тогда y=a – частное решение.

Однородные уравнения и уравнения, приводящие к однородным.

По Степанову:

Проверка уравнения на однородное

В исходное уравнение:

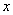
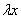
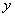
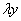
вместо подставляем , вместо подставляем , производную не трогаем:

Буква лямбда – это некоторый абстрактный числовой параметр, дело не в самих лямбдах, и не в их значениях, а дело вот в чём:

Если в результате преобразований удастся сократить ВСЕ «лямбды» (т.е. получить исходное уравнение), то данное дифференциальное уравнение является однородным.

Очевидно, что лямбды сразу сокращаются в показателе степени:

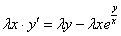
Теперь в правой части выносим лямбду за скобки:

Обе части уравнения можно сократить на эту самую лямбду:

В результате все лямбды исчезли как сон, как утренний туман, и мы получили исходное уравнение.

Вывод: Данное уравнение является однородным.

Приведение к уравнению с разделяющимися переменными

Однородное уравнение приводится к уравнению с разделяющимися переменными путем замены y=tx, где t-функция, зависящая от x.

Уравнения, приводимые к однородным

К однородным уравнениям первого порядка приводится уравнение вида:

Как определить, что дифференциальное уравнение приводится к однородному

Для того, чтобы определить, что дифференциальное уравнение приводится к однородному, нужно выделить две линейные формы:
a₁ x + b₁ y + c₁, a₂ x + b₂ y + c₂, и выполнить замену:

Если после преобразований t сократится, то это уравнение приводится к однородному.

Решение дифференциального уравнения, приводящегося к однородному уравнению

Решаем систему уравнений:

Здесь возможны три случая:

1) Система имеет бесконечное множество решений (прямые a₁ x + b₁ y + c₁ = 0 и a₂ x + b₂ y + c₂ = 0совпадают). В этом случае

Это простейший вид уравнения с разделяющимися переменными:

Это уравнение приводится к уравнению с разделяющимися переменными подстановкой
z = a₂ x + b₂ y + c₂.

3) Система имеет одно решение (прямые a₁ x + b₁ y + c₁ = 0 и a₂ x + b₂ y + c₂ = 0 пересекаются в одной точке). Обозначим это решение x₀, y₀. Тогда

Делаем подстановку x = t + x₀, y = u + y₀. Тогда dx = dt, dy = du,

Это однородное дифференциальное уравнение первого порядка. Оно решается подстановкой u = zt, где z — функция от t.

Линейные уравнения первого порядка.

Решение линейного дифференциального уравнения с помощью интегрирующего множителя

Рассмотрим линейное неоднородное дифференциальное уравнение первого порядка:

Существует три способа решения этого уравнения:

• метод интегрирующего множителя;
• метод введения двух функций (Бернулли);
• метод вариации постоянной (Лагранжа).

Рассмотрим метод решения линейного дифференциального уравнения первого порядка с помощью интегрирующего множителя.

Умножим исходное уравнение на интегрирующий множитель —

:

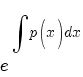
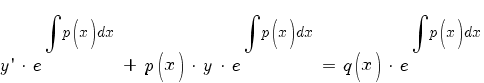(1)

Далее замечаем, что производная от интеграла равна подынтегральной функции:

По правилу дифференцирования сложной функции:

По правилу дифференцирования произведения:

Подставляем в (1):

Умножаем на 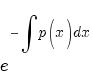. Получаем общее решение линейного дифференциального уравнения первого порядка:

Видео:11. Уравнения в полных дифференциалахСкачать

Решение дифференциальных уравнений с помощью интегрирующего множителя

Видео:7. Линейные дифференциальные уравнения первого порядка. Метод Бернулли.Скачать

Определение интегрирующего множителя

Видео:12. Интегрирующий множитель. Уравнения в полных дифференциалахСкачать

Свойства интегрирующего множителя

Рассмотрим дифференциальное уравнение:
(1)
Если

То левая часть уравнения (1) не является дифференциалом некоторой функции. Однако при выполнении условий существования единственного решения уравнения (1), его можно привести к уравнению в полных дифференциалах умножением на некоторую функцию от переменных и .

Теорема о существовании интегрирующего множителя

Дифференциальное уравнение первого порядка имеет бесконечное число интегрирующих множителей (при выполнении условий существования единственного решения).

Докажем это. Если существует решение уравнения (1), то его общий интеграл можно представить в виде:

Возьмем дифференциал:
(2)
Отсюда:

С другой стороны, из уравнения (1):

Левые части уравнений равны. Поэтому равны правые части:

Или:

Тогда уравнение (2) можно переписать в виде:

Исходное уравнение (1) превратилось в полный дифференциал умножением на интегрирующий множитель:

что доказывает существование интегрирующего множителя.

Покажем, что существует бесконечно много интегрирующих множителей. Для этого выражение:

Умножим на произвольную функцию от :

Это выражение также является полным дифференциалом, поэтому множитель

также является интегрирующим множителем. Поскольку – это произвольная функция, то можно построить бесконечное число интегрирующих множителей.

Теорема об отношении интегрирующих множителей

Если известны два интегрирующих множителя, отношение которых не является постоянной, то их отношение является общим интегралом дифференциального уравнения:
.

Действительно, поскольку , то

Но, поскольку, – общий интеграл уравнения, то

Отсюда:

Видео:Дифференциальные уравнения, 4 урок, Линейные дифференциальные уравнения первого порядкаСкачать

Методы определения интегрирующего множителя

Хотя каждое уравнение имеет интегрирующий множитель, совсем не обязательно, что он выражается через известные функции. Поэтому найти интегрирующий множитель можно не всегда. Но даже если интегрирующий множитель выражается через известные функции, нет методов, следуя которыми, можно было бы с гарантией определить его. Поэтому, при решении уравнений, следует проверить, не принадлежит ли уравнение одному из известных типов. И в том случае, если оно не принадлежит ни одному из известных типов, попытаться найти интегрирующий множитель.

Ниже описан ряд методов, с помощью которых, в некоторых случаях, можно найти интегрирующий множитель.

Метод последовательного выделения дифференциала

Этот метод аналогичен методу выделения полного дифференциала для уравнений в полных дифференциалах. Только здесь полный дифференциал удается выделить, умножая уравнение на множители. Для этого применяем формулы дифференцирования, записанные в дифференциальной форме:
;
;
;
.
В этих формулах и – произвольные выражения, составленные из любых комбинаций переменных.

Пример

Сгруппируем члены:

Замечаем, что

Подставляем и делим на . При уравнение принимает вид:

Но:
;
.
Подставляем:

Отсюда:
.

Мы получили решение, справедливое при . Теперь рассмотрим случай . Нетрудно видеть, что постоянная также является решением уравнения. Поэтому добавим ее в окончательный результат.

В процессе выделения дифференциала мы разделили уравнение на . Поэтому интегрирующий множитель оказался равным
.

Метод группировки членов уравнения

Если сразу найти интегрирующий множитель не удается, то можно попытаться сгруппировать члены уравнения. Пусть мы имеем уравнение:

разбиваем его на сумму слагаемых:

Пусть первое слагаемое имеет интегрирующий множитель:

Умножаем уравнение на :

Далее следует подобрать такую функцию от , чтобы при умножении на нее, второе слагаемое стало полным дифференциалом:
.
Первое слагаемое при этом остается полным дифференциалом:
.
Тогда:

Далее следует подобрать такую функцию от , чтобы при умножении на нее, следующее слагаемое стало полным дифференциалом. И так далее, пока все выражение станет полным дифференциалом.

Пример

Сгруппируем члены и разделим на :

Первые два члена являются полным дифференциалом:
, подставляем:

Теперь нужно подобрать такую функцию от , чтобы оставшееся выражение стало полным дифференциалом. Методом перебора различных вариантов находим, что для этого нужно разделить уравнение на . Тогда при и уравнение примет вид:
;
;
;
.
Отсюда
.

Теперь рассмотрим случаи и . Зависимости и удовлетворяют исходному уравнению, но не входят в полученный общий интеграл. Поэтому добавим их в окончательный результат.

Определение интегрирующего множителя заданного вида

В предыдущем примере мы получили два члена

уравнения, для которых нужно было подобрать интегрирующий множитель вида . Мы это сделали методом подбора. То есть просто угадали, что интегрирующий множитель имеет вид
.
На самом деле процедуры подбора можно избежать. Можно точно определить, имеется ли для заданного уравнения интегрирующий множитель заданного вида. И если имеется, то определить его.

Пусть имеется уравнение
,
для которого ищется интегрирующий множитель вида

где – заданная функция от переменных и .
Найдем такой интегрирующий множитель, или определим, что множителя такого вида не существует.

Для этого умножим исходное уравнение на :

Это уравнение будет уравнением в полных дифференциалах при выполнении условия
.
Или:
;

Теперь положим, что – это функция от , где – это заданная функция переменных и . Тогда
.
Подставляем:
;
.
Отсюда:
(3)
Левая часть этого уравнения является функцией от . Поэтому и правая часть тоже должна быть функцией от .

Таким образом, интегрирующий множитель заданного вида существует, если правая часть уравнения (3) является функцией от u :

В этом случае

Или

Интегрируем:

Отсюда

Поскольку постоянная для интегрирующего множителя никакого значения не имеет, положим :

Пример

Проверить, имеет ли уравнение:

Интегрирующий множитель вида . И если имеет, то найти его.

В нашем случае:
;
;
;
.
Интегрирующий множитель вида существует, поскольку есть функция от :

Находим его.
;
.
Опускаем знак модуля.

Уравнение имеет интегрирующий множитель
.

Использованная литература:
В.В. Степанов, Курс дифференциальных уравнений, «ЛКИ», 2015.
Н.М. Гюнтер, Р.О. Кузьмин, Сборник задач по высшей математике, «Лань», 2003.

Автор: Олег Одинцов . Опубликовано: 12-08-2012 Изменено: 01-03-2016

Видео:Видеоурок "Интегрирующий множитель"Скачать

Уравнения в полных дифференциалах. Интегрирующий множитель

Дифференциальное уравнение первого порядка вида

называется уравнением в полных дифференциалах , если его левая часть представляет полный дифференциал некоторой функции , т.е.

Теорема. Для того, чтобы уравнение (1) являлось уравнением в полных дифференциалах, необходимо и достаточно, чтобы в некоторой односвязной области изменения переменных и выполнялось условие

Общий интеграл уравнения (1) имеет вид или

Пример 1. Решить дифференциальное уравнение .

Решение. Проверим, что данное уравнение является уравнением в полных дифференциалах:

так что т.е. условие (2) выполнено. Таким образом, данное уравнение есть уравнение в полных дифференциалах и

поэтому , где пока неопределенная функция.

Интегрируя, получаем . Частная производная найденной функции должна равняться , что дает откуда так что Таким образом, .

Общий интеграл исходного дифференциального уравнения .

При интегрировании некоторых дифференциальных уравнений можно так сгруппировать члены, что получаются легко интегрируемые комбинации.

Пример 2. Решить дифференциальное уравнение .

Решение. Здесь , так что условие (2) выполнено и, следовательно, данное уравнение есть уравнение в полных дифференциалах. Это уравнение легко привести к виду непосредственной группировкой его членов. С этой целью перепишем его так:

Поэтому изначальное уравнение можно записать в виде

Следовательно, есть общий интеграл исходного уравнения.

Видео:Математика без Ху!ни. Линейное неоднородное уравнение 1 порядка. Метод вариации постоянной.Скачать

Интегрирующий множитель

В некоторых случаях, когда уравнение (1) не является уравнением в полных дифференциалах, удается подобрать функцию , после умножения на которую левая часть (1) превращается в полный дифференциал

Такая функция называется интегрирующим множителем . Из определения интегрирующего множителя имеем

Мы получили для нахождения интегрирующего множителя уравнение в частных производных.

Отметим некоторые частные случаи, когда удается сравнительно легко найти решение уравнения (5), т.е. найти интегрирующий множитель.

1. Если , то и уравнение (5) примет вид

Для существования интегрирующего множителя, не зависящего от , необходимо и достаточно, чтобы правая часть (6) была функцией только . В таком случае найдется квадратурой.

Пример 3. Решить уравнение .

Решение. Здесь . Имеем

Уравнение есть уравнение в полных дифференциалах. Его левую часть можно представить в виде

2. Аналогично, если есть функция только , то уравнение (1) имеет интегрирующий множитель , зависящий только от .

Пример 4. Решить уравнение .

Решение. Здесь . Имеем

Уравнение является уравнением в полных дифференциалах. Его можно записать в виде

Пример 5. Решить уравнение , если его интегрирующий множитель имеет вид .

Решение. Положим , тогда , и, следовательно,

Уравнение (5) для нахождения интегрирующего множителя будет иметь вид

и, значит, , откуда , т.е. . Умножая данное уравнение на , получим

Это есть уравнение в полных дифференциалах и его общий интеграл согласно (3) будет

После несложных преобразований будем иметь .

📸 Видео

#Дифуры I. Урок 7. Интегрирующий множительСкачать

Решение системы дифференциальных уравнений методом ЭйлераСкачать

16. Линейные неоднородные дифференциальные уравнения 2-го порядка с постоянными коэффициентамиСкачать

#Дифуры I. Урок 5. Линейные дифференциальные уравнения. Метод БернуллиСкачать

Видеоурок "Нахождение частных решений по виду правой части"Скачать

9. Метод вариации произвольной постоянной ( метод Лагранжа ). Линейные дифференциальные уравнения.Скачать

Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентамиСкачать

Задача Коши ➜ Частное решение линейного однородного дифференциального уравненияСкачать

Метод Лагранжа & Метод Бернулли ★ Решение линейных неоднородных дифференциальных уравненийСкачать

13. Как решить дифференциальное уравнение первого порядка?Скачать