план-конспект урока по алгебре (8 класс) по теме
Одним из главных аспектов современного урока, согласно требованиям ФГОС ООО, является деятельностный аспект. Применение деятельностного подхода в обучении математике обеспечивает развитие у школьников основной школы высокого уровня знаний, умений, приемов мышления, которые в свою очередь способствуют повышению качества обучения.
Видео:Линейная функция: краткие ответы на важные вопросы | Математика | TutorOnlineСкачать

Скачать:
| Вложение | Размер |
|---|---|
| uravnenie_pryamoy_vida_ukhv.doc | 249.5 КБ |
| uravnenie_pryamoy_vida_ukhv.pptx | 173.43 КБ |
Видео:Линейная функция и ее график. 7 класс.Скачать

Предварительный просмотр:
Тема: Уравнение прямой вида y = kx + l.
- Предметные: знать геометрический смысл коэффициентов к и l в уравнении прямой у = кх + l, уметь по уравнению прямой определять взаимное расположение графиков
- Метапредметные: развивать навыки исследовательской работы, систематизации и обобщения, формировать умение четко и ясно излагать мысли.
- Личностные: развитие личности учащихся на основе универсальных учебных действий: формировать учебно-познавательный интерес к предмету, готовность и способность к саморазвитию, умение оценивать свою работу, навыки сотрудничества
Материально-техническое обеспечение урока:
презентация к уроку, задания для групп с исследовательской работой (приложение 1),
материалы для домашней работы (приложение 2)
Методы организации работы:
- создание проблемной ситуации
- организация исследовательской деятельности
- метод рефлексивной самоорганизации (деятельностный метод)
Приветствие, эмоциональный настрой.
На доске написаны слова : « Скажи мне – и я забуду, покажи мне – и я запомню, дай сделать – и я пойму»
- Проверка уровня усвоения изученного материала, готовности к работе на уроке. Актуализация опорных знаний (презентация):
Какое уравнение называется линейным уравнением с двумя переменными?
Уравнение вида ax +by=c, где a, b,c – некоторые числа, а х, у – переменные.
Что является решением линейного уравнения с двумя переменными?
Пара чисел (х ; у), которая обращает уравнение в верное равенство.
Что является графиком линейного уравнения с двумя переменными?
Графиком является прямая.
Как из уравнения вида ax +by=c получить уравнение вида у=kx + l?
Решить уравнение относительно переменной у.
Что является графиком уравнения у = kх ?
Графиком является прямая, проходящая через начало координат.
В каких координатных четвертях расположен график прямой у=kx ,
если k > 0? ( График расположен в 1 и 3 координатных четвертях)
Что является графиком уравнения у = l?
Графиком является прямая, параллельная оси Х и проходящая через точку c координатами (0, l).
Слайд №8: На чертеже изображены три прямые. Каждой прямой поставить в соответствии уравнение: 1) у = 1,5х 2) у = 1,5 3) у = — 1,5х
Запишите уравнение прямой, параллельной прямой у = 0,5 х + 2 и проходящей через точку (4; — 1).
2. Актуализация и фиксирование затруднения в поставленной задаче (проблемная ситуация). (4-5 мин)
Готовы ли мы выполнить такое задание? Достаточно ли знаем? Как вы думаете, от чего зависит расположение прямой в координатной плоскости? (от коэффициентов)
3. Постановка учебной задачи: выясним, как влияют коэффициенты на взаимное расположение прямых в координатной плоскости. Цели для учеников:
- знать геометрический смысл коэффициентов k и l в уравнении прямой
2. уметь по уравнению прямых определять взаимное расположение графиков
4. Проведем исследовательскую работу (работа выполняется по группам в программе УМК «Живая математика»). Для каждой группы приготовлены карточки для исследовательской работы (приложение 1).
Выясним, какую роль играет коэффициент k
1 группа: Построить в одной и той же координатной плоскости прямые у = 3х,
у = 3х + 3 и у = 3х — 4
2 группа: Построить в одной и той же координатной плоскости прямые у = — 3х,
у = — 3х +3 и у = -3х — 1
3 группа: Построить в одной и той же координатной плоскости прямые у = 2х,
у = 2х + 3 и у = 2х- 3
Что общего у уравнений? Что общего у прямых, являющихся графиками этих уравнений? После построения ученики в группах обсуждают полученный результат, формулируют свои выводы, один человек от группы выступает с отчетом о работе.
1. если коэффициенты k равны, то прямые параллельны
2. если k > 0, то угол острый, а если k
k — угловой коэффициент прямой.
Если угловые коэффициенты одинаковы, то прямые параллельны.
Если же угловые коэффициенты различны, то прямые пересекаются.
Если k > 0, то угол наклона к положительному направлению оси Х — острый, а если k
Выясним, какую роль играет коэффициент l .
Проведем аналогичную исследовательскую работу.
1 группа: Построить в одной и той же координатной плоскости прямые у = 2 у = 2х + 2 и у = — х +2
2 группа: Построить в одной и той же координатной плоскости прямые у = — 2,
у = х – 2 и у = -2х — 2
3 группа: Построить в одной и той же координатной плоскости прямые у = 4, у = 0,6х + 4 и у = -3х + 4
Что общего у уравнений? Что общего у прямых, являющихся графиками этих уравнений?
Проводится аналогичная работа в группах.
После исследования делаем выводы: в каждом случае мы получили пучок прямых, приходящих через точку (0; l).
Прямая y = kx + l пересекает ось у в точке (0; l)
Если l >0 , то точка пересечения расположена выше оси Х
Учитель: Итак, посмотрите, сколько полезной информации мы можем извлечь из уравнения прямой: Коэффициенты k и l позволяют судить о положении прямой в координатной плоскости: коэффициент к определяет угол наклона прямой к положительному направлению оси ох, а коэффициент l показывает, в какой точке прямая пересекает ось у.
- Первичное закрепление: задания выполняются устно, с пояснениями и комментариями..
1. Для каждой прямой назвать угловой коэффициент и точку пересечения с осью Y. а) у = х + 7 б) у = -0,4х + 3 в) у = 2,4х — 5 г) у = 6 — 3х
2. Запишите уравнение прямой, если известен ее угловой коэффициент k и точка, в которой эта прямая пересекает ось у:
а) k = 2, А(0,1) б) к = — 4, А(0, -0,5) в) к = -0,5, А(0;0)
3. На доске схематично показать расположение в координатной плоскости прямой, заданной уравнением у = 3,2х — 3 у = 3,2х + 4 у = 0,6х -3 у = -2х +4 (первую — учитель с пояснениями, дальше по одной ученики с комментарием)
6. Включение в систему знаний, разрешение проблемной ситуации . (возвращаемся к задаче из ГИА): Запишите уравнение прямой, параллельной прямой у = 0,5 х + 2 и проходящей через точку (4; — 1).
- k = 0,5 , т.к. прямые параллельны у = 0,5х + l
- прямая проходит через точку (4;-1), значит -1 = 0,5· 4 + l, l = -3
- у = 0,5х -3
- Самостоятельная работа с самопроверкой и коррекция.
- Отметьте пары параллельных прямых.
а) y = 2х – 3 и у = 3х – 2
б) y = 5х – 2 и у = 5х — 4
в) y = 4х – 3 и у = -4х +3
г) y = -2х – 3 и у = 3 -2х
- Назовите координаты точки в которой прямая y=-5x+4 пересекает ось Оу.
- Дана прямая у = — 4х + 3. Запишите уравнение какой-нибудь прямой:
а) имеющей такую же точку пересечения с осью у;
б) имеющей такой же угловой коэффициент.
4) Изобразить схематически на координатной плоскости прямые:
а) у= 3х- 2 б) у = 3х +2 в) у=3х г) у = — 2
8. Рефлексия учебной деятельности на уроке (итог урока):
Слайд № 19 – изображение дерева
Если вы считаете, что вы поняли тему сегодняшнего урока, то наклейте зеленый листочек на дерево.
Если вы считаете, что не достаточно усвоили материал, то наклейте желтый листочек на дерево.
Если вы считаете, что вы не поняли тему сегодняшнего урока, то наклейте красный листочек на дерево.
Я увижу цветовой индекс урока.
Ученики наклеивают листочек нужного цвета.
9. Домашнее задание:
- придумать и решить 3 различных задачи, аналогичных тем, которые выполняли на уроке, записать их для взаимообмена заданиями.
- Сделать кластер по теме урока (материалы для кластера выдаются каждому)- приложение 2.
Карточка для выполнения исследовательской работы
1 часть «Коэффициент k»
- Используя программу «Живая математика», построить в одной и той же координатной плоскости прямые:
у = 3х; у = 3х + 3; у = 3х – 4
- Заполнить таблицу:
| Функция — это зависимость y от x, где x является независимой переменной или аргументом функции, а y — зависимой переменной или значением функции. |
|---|
Задать функцию значит определить правило, следуя которому по значениям независимой переменной можно найти соответствующие значения функции. Вот какими способами ее можно задать:
Табличный способ помогает быстро определить конкретные значения без дополнительных измерений или вычислений.
Аналитический способ — через формулы. Компактно, и можно посчитать функцию при произвольном значении аргумента из области определения.
Словесный способ.
Графический способ — наглядно. Его мы и разберем в этой статье.
| График функции — это множество точек (x; y), где x — это аргумент, а y — значение функции, которое соответствует данному аргументу. |
|---|
Видео:ЛИНЕЙНЫЕ УРАВНЕНИЯ - Как решать линейные уравнения // Подготовка к ЕГЭ по МатематикеСкачать

Понятие линейной функции
| Линейная функция — это функция вида y = kx + b, где х — независимая переменная, k, b — некоторые числа. При этом k — угловой коэффициент, b — свободный коэффициент. |
|---|
Геометрический смысл коэффициента b — длина отрезка, который отсекает прямая по оси OY, считая от начала координат.
Геометрический смысл коэффициента k — угол наклона прямой к положительному направлению оси OX, считается против часовой стрелки.
Если известно конкретное значение х, можно вычислить соответствующее значение у.
Нам дана функция: у = 0,5х — 2. Значит:
если х = 0, то у = -2;
если х = 2, то у = -1;
если х = 4, то у = 0 и т. д.
Для удобства результаты можно оформлять в виде таблицы:
| х | 0 | 2 | 4 |
| y | -2 | -1 | 0 |
Графиком линейной функции является прямая. Для ее построения достаточно двух точек, координаты которых удовлетворяют уравнению функции.
Угловой коэффициент отвечает за угол наклона прямой, свободный коэффициент — за точку пересечения графика с осью ординат.
k и b — это числовые коэффициенты функции. На их месте могут стоять любые числа: положительные, отрицательные или дроби.
Давайте потренируемся и определим для каждой функций, чему равны числовые коэффициенты k и b.
| Функция | Коэффициент k | Коэффициент b |
|---|---|---|
| y = 2x + 8 | k = 2 | b = 8 |
| y = −x + 3 | k = −1 | b = 3 |
| y = 1/8x − 1 | k = 1/8 | b = −1 |
| y = 0,2x | k = 0,2 | b = 0 |
Может показаться, что в функции y = 0,2x нет числового коэффициента b, но это не так. В данном случае он равен нулю. Чтобы не поддаваться сомнениям, нужно запомнить: в каждой функции типа y = kx + b есть коэффициенты k и b.
Видео:Линейная Функция — как БЫСТРО построить график и получить 5-куСкачать

Свойства линейной функции
Область определения функции — множество всех действительных чисел.
Множеством значений функции является множество всех действительных чисел.
График линейной функции — прямая. Для построения прямой достаточно знать две точки. Положение прямой на координатной плоскости зависит от значений коэффициентов k и b.
Функция не имеет ни наибольшего, ни наименьшего значений.
Четность и нечетность линейной функции зависят от значений коэффициентов k и b:
b ≠ 0, k = 0, значит, y = b — четная;
b = 0, k ≠ 0, значит, y = kx — нечетная;
b ≠ 0, k ≠ 0, значит, y = kx + b — функция общего вида;
b = 0, k = 0, значит, y = 0— как четная, так и нечетная функция.
Свойством периодичности линейная функция не обладает, потому что ее спектр непрерывен.
График функции пересекает оси координат:
ось абсцисс ОХ — в точке (−b/k; 0);
ось ординат OY — в точке (0; b).
x = −b/k — является нулем функции.
Если b = 0 и k = 0, то функция y = 0 обращается в ноль при любом значении переменной х.
Если b ≠ 0 и k = 0, то функция y = b не обращается в нуль ни при каких значениях переменной х.
Функция монотонно возрастает на области определения при k > 0 и монотонно убывает при k 0 функция принимает отрицательные значения на промежутке (−∞; −b/k) и положительные значения на промежутке (−b/k; +∞).
При k 0, то этот угол острый, если k
Видео:Линейное уравнение с двумя переменными. 7 класс.Скачать

Построение линейной функции
В геометрии есть аксиома: через любые две точки можно провести прямую и притом только одну. Исходя из этой аксиомы следует: чтобы построить график функции вида у = kx + b, достаточно найти всего две точки. А для этого нужно определить два значения х, подставить их в уравнение функции и вычислить соответствующие значения y.
Например, чтобы построить график функции y = 1/3x + 2, можно взять х = 0 и х = 3, тогда ординаты этих точек будут равны у = 2 и у = 3. Получим точки А (0; 2) и В (3; 3). Соединим их и получим такой график:
В уравнении функции y = kx + b коэффициент k отвечает за наклон графика функции:
если k > 0, то график наклонен вправо;
если k 0, то график функции y = kx + b получается из y = kx со сдвигом на b единиц вверх вдоль оси OY;
если b 0, то график функции y = kx + b выглядит так:
0″ src=»https://user84060.clients-cdnnow.ru/uploads/5fc1049363f94987951092.png» style=»height: 600px;»>
Если k > 0 и b > 0, то график функции y = kx + b выглядит так:
0 и b > 0″ src=»https://user84060.clients-cdnnow.ru/uploads/5fc104b2640e6151326286.png» style=»height: 600px;»>
Если k > 0 и b
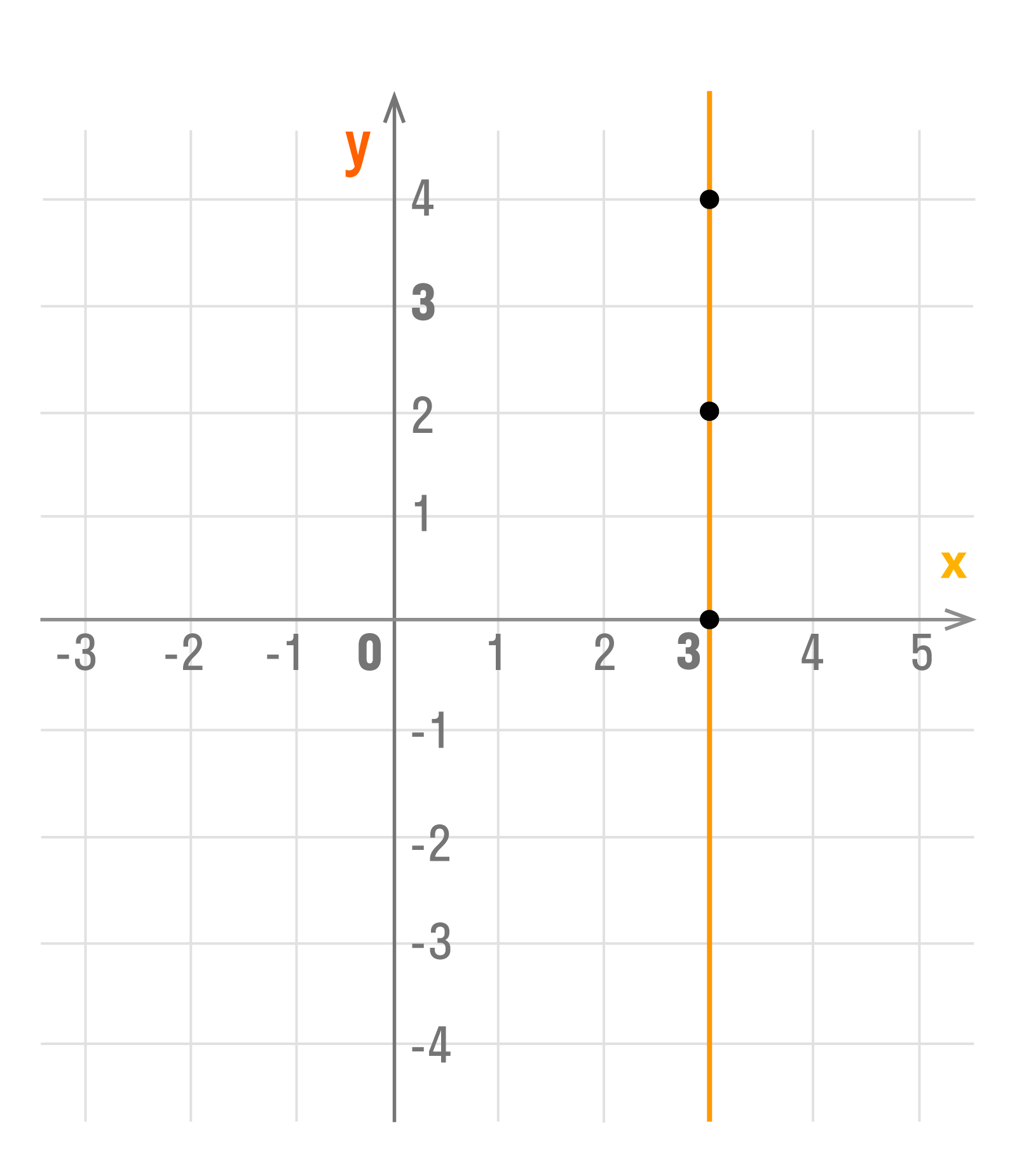
В задачах 7 класса можно встретить график уравнения х = а. Он представляет собой прямую линию, которая параллельна оси ОY все точки которой имеют абсциссу х = а.
Важно понимать, что уравнение х = а не является функцией, так как различным значениям аргумента соответствует одно и то же значение функции, что не соответствует определению функции.
Например, график уравнения х = 3:
Условие параллельности двух прямых:
График функции y = k1x + b1 параллелен графику функции y = k2x + b2, если k1 = k2.
Условие перпендикулярности двух прямых:
График функции y = k1x + b1 перпендикулярен графику функции y = k2x + b2, если k1k2 = −1 или k1 = −1/k2.
Точки пересечения графика функции y = kx + b с осями координат:
С осью ОY. Абсцисса любой точки, которая принадлежит оси ОY равна нулю. Поэтому, чтобы найти точку пересечения с осью ОY, нужно в уравнение функции вместо х подставить ноль. Тогда получим y = b.
Координаты точки пересечения с осью OY: (0; b).
С осью ОХ. Ордината любой точки, которая принадлежит оси ОХ равна нулю. Поэтому, чтобы найти точку пересечения с осью ОХ, нужно в уравнение функции вместо y подставить ноль. И получим 0 = kx + b. Значит x = −b/k.
Координаты точки пересечения с осью OX: (−b/k; 0).
Видео:Построить график ЛИНЕЙНОЙ функции и найти:Скачать

Решение задач на линейную функцию
Чтобы решать задачи и строить графики линейных функций, нужно рассуждать и использовать свойства и правила выше. Давайте потренируемся!
Пример 1. Построить график функции y = kx + b, если известно, что он проходит через точку А (-3; 2) и параллелен прямой y = -4x.
В уравнении функции y = kx + b два неизвестных параметра: k и b. Поэтому в тексте задачи нужно найти два условия, которые характеризуют график функции.
Из того, что график функции y = kx + b параллелен прямой y = -4x, следует, что k = -4. То есть уравнение функции имеет вид y = -4x + b.
Осталось найти b. Известно, что график функции y = -4x + b проходит через точку А (-3; 2). Подставим координаты точки в уравнение функции и мы получим верное равенство:
Таким образом, нам надо построить график функции y = -4x — 10
Мы уже знаем точку А (-3; 2), возьмем точку B (0; -10).
Поставим эти точки в координатной плоскости и соединим прямой:
Пример 2. Написать уравнение прямой, которая проходит через точки A (1; 1); B (2; 4).
Если прямая проходит через точки с заданными координатами, значит координаты точек удовлетворяют уравнению прямой y = kx + b.
Следовательно, если координаты точек подставить в уравнение прямой, то получим верное равенство.
Подставим координаты каждой точки в уравнение y = kx + b и получим систему линейных уравнений.
Вычтем из второго уравнения системы первое, и получим k = 3.
Подставим значение k в первое уравнение системы, и получим b = -2.
Ответ: уравнение прямой y = 3x — 2.
Видео:запишите уравнения прямых в виде у=кх+lСкачать

Решение линейных уравнений онлайн
Линейным называется уравнение вида:
Линейное уравнение всегда имеет только один корень. Данный калькулятор предназначен для решения таких уравнений. Для получения решения уравнения, необходимо ввести уравнение в естественной форме записи. Помимо десятичных чисел, например 2.43, в калькулятор можно вводить дроби (1/3, -5/8 и т.д.). Кроме того, уравнение может содержать буквы (параметры). В этом случае решение будет дано в общем виде.
📽️ Видео
7 класс, 8 урок, Линейное уравнение с двумя переменными и его графикСкачать

Как построить график линейной функции.Скачать

ГРАФИК ЛИНЕЙНОГО УРАВНЕНИЯ С ДВУМЯ ПЕРЕМЕННЫМИ 7 КЛАСС видеоурокСкачать

Линейное уравнение с одной переменной. 6 класс.Скачать

ГРАФИК ФУНКЦИИ y = kx + b | линейная функция | 7 классСкачать

Как решать уравнения? уравнение 7 класс. Линейное уравнениеСкачать

Видеоурок. 7 класс. Решение линейных уравнений с одним неизвестнымСкачать

ЛИНЕЙНАЯ ФУНКЦИЯ y=kx график линейной функции 7 и 8 классСкачать

Алгебра 7 класс (Урок№43 - Решение линейных уравнений с одним неизвестным.)Скачать

Алгебра 7 класс. 8 октября. y=kxСкачать