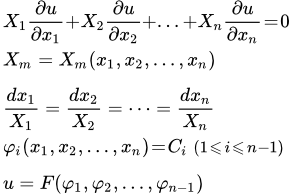Решение квазилинейных уравнений в частных производных первого порядка методом характеристик

Как и выше, мы рассмотрим сначала случай двух независимых переменных х и у.

Определение. Квазилинейным уравнением в частных производных первого порядка называется уравнение вида

где а(х, у, и), Ь(х, у, и) и с(х, у, и) — заданные в некоторой области G 3 непрерывно дифференцируемые функции, причем а(х, у, и), Ь(х, у, и) и с(х, у, и) в области G не обращаются в нуль одновременно.

Замечание. Очевидно, линейное неоднородное уравнение (2.7) является частным случаем квазилинейного уравнения, так как если в (2.25) положить с(х, у, и) = /(х, у) — с(х, у)и, мы получим уравнение (2.7).

Решение квазилинейного уравнения (2.25) будем искать в неявном виде, заданном равенством

По правилу дифференцирования функции и(х, у), заданной неявно равенством (2.26), находим: и_х = , и,, = . Подставив эти

выражения в уравнение (2.25), получим уравнение для функции |/(х, у, и):

Оно совпадает с уравнением (2.15) с точностью до обозначений неизвестной функции и одной из переменных. Поэтому для нахождения общего решения |/(х, у, и) уравнения (2.27) необходимо найти два независимых первых интеграла (рДх, у, и) = Cj и ср₂(х, у, и) = С₂ характеристической системы этого уравнения

и положить по аналогии с (2.18)

где Ф(ср_1? е G и эти переменные считаются независимыми. Но можно допустить существование и таких решений и = и(х, у) уравнения (2.25), для которых (2.27) удовлетворяется тождественно лишь по переменным (х, у) е D только при и = и(х, у). Эти решения могут и не содержаться в формуле (2.31); они называются специалъними решениями. Дополнительный анализ показывает, что в содержательных задачах специальное решение — это исключительный случай, не представляющий интереса, см. [7, 9]. Поэтому обычно рассматривают формулу (2.31) как неявное представление общего решения квазилинейного уравнения (2.25).

Пример 2.9. Найти общее решение уравнения хи_х + уи_у = и.

Другой первый интеграл

получаем из уравнения — = —.

Таким образом, неявное представление общего решения уравнения в частных производных имеет вид

Поскольку от переменной и зависит только один из первых интегралов, можно записать: хе

и = ‘<'(х 2 + у 2 ), где Ч'(ф) — произвольная непрерывно дифференцируемая функция. Отсюда находим явное представление общего решения:

где Ч'(ф) = 1пЧДх 2 + у 2 ) — произвольная гладкая функция. >

Замечание. В отличие от линейного однородного уравнения (2.9) характеристики квазилинейного уравнения (2.25) лежат не в пространстве R 2 переменных (х, у), а в пространстве R 3 переменных (х, у, и). С учетом этого возможна следующая геометрическая интерпретация связи интегральной поверхности квазилинейного уравнения в частных производных и его характеристик.

Теорема 2.5. Для того чтобы поверхность Е в пространстве R 3 переменных (х, у, и) была интегральной поверхностью квазилинейного уравнения (2.25), необходимо и достаточно, чтобы через любую точку поверхности Е проходила характеристика данного уравнения, целиком лежащая на этой поверхности.

2 описывает интегральную поверхность Е уравнения (2.25), а Р(х, у, и(х, у)) — произвольная точка этой поверхности и М(х, у) — проекция точки Р на плоскость Оху, рис. 2.3.

Рассмотрим систему обыкновенных дифференциальных уравнений:

Пусть Г: х = x(t), у = y(t) — интегральная кривая (решение системы (2.32)), проходящая через точку М. В пространстве R 3 переменных (х, у, и) ей соответствует кривая у: х = x(t), у = y(t), и = u(x(t), y(t)), проходящая через точку Р и, по построению, лежащая на интегральной поверхности и = и(х, у). Убедимся в том, что кривая у является характеристикой уравнения (2.25), т.е. функции х = x(f), у = y(t) и и = u(x(t), y(t)) удовлетворяют характеристической системе (2.28).

В силу (2.32) первые два уравнения системы (2.28) удовлетворяются. Проверим выполнение третьего уравнения. По правилу дифференцирования сложной функции получаем:

По условию функция и = и(х, у) является решением квазилинейного уравнения (2.25), поэтому правая часть последнего из равенств (2.33) равна с(х, у, и). Таким образом, мы убедились в том, что du

• — = с(х, у, и), т.е. и третье уравнение характеристической системы dt
• (2.28) удовлетворяется.

Значит, кривая у, лежащая на интегральной поверхности X и проходящая через точку Р, действительно является характеристикой уравнения (2.25). В силу произвольности точки Р необходимость утверждения теоремы доказана.

2. Достаточность. Пусть поверхность X описывается уравнением и = и(х, у) и через любую точку этой поверхности проходит характеристика уравнения (2.25), целиком лежащая на этой поверхности. Выберем произвольную точку Р(х₀, у₀, и(х₀, у₀)) е X и рассмотрим характеристику у, проходящую через эту точку. Поскольку кривая у описывается характеристической системой (2.29), она является векторной линией векторного поля а = (а(х, у, и), Ь(х, у, и), с(х, у, и)), см. (П2.2). Поэтому вектор а(Р) направлен по касательной к кривой у. С другой стороны, вектор нормали к поверхности и = и(х, у) в точке Р имеет вид

Поскольку векторы а(Р) и п(/ > ) ортогональны, их скалярное произведение равно нулю, т.е.

Последнее равенство означает, что функция и(х, у) удовлетворяет уравнению (2.25) в точке (х₀, у₀) е D- в СИЛ У произвольности точки Ре! можно утверждать, что эта функция является решением уравнения (2.25) в области D, т.е. Е есть интегральная поверхность этого уравнения. >

Замечание. Геометрический смысл теоремы 2.5 состоит в том, что любая интегральная поверхность квазилинейного уравнения (2.25) состоит из характеристик этого уравнения (рис. 2.4).

Видео:Линейные дифференциальные уравнения в частных производныхСкачать

КВАЗИЛИНЕЙНЫЕ УРАВНЕНИЯ В ЧАСТНЫХ ПРОИЗВОДНЫХ ПЕРВОГО ПОРЯДКА

Рассмотрим квазилинейное уравнение в частных производных первого порядка

где и — неизвестная функция от независимых переменных t, х_х, х₂, . х_п, Х_х, Х₂, . Х„ и В— заданные функции своих аргументов. Считаем, что Х₁,Х₂. Х_п, Be C>_XU(D), D с В п+2 .

Сведем это уравнение к линейному однородному уравнению в частных производных первого порядка. Будем искать решение и в неявной форме

где функция и непрерывно дифференцируема по своим аргументам и

Если u(t, х) — решение уравнения (50), то и(t, х, u(t, х)) = 0. Продифференцируем данное тождество по переменным t, х_х, х_п, получим равенства

1 (l? n+1 )— произвольная функция такая, что равенство (55) разрешимо относительно переменной и.

Доказательство. Доказательство состоит из объединения теорем 8 и 9.

Пример 1. Найти общее решение квазилинейного уравнения в частных производных первого порядка.

Составляем систему для характеристик

и находим общее решение

Разрешая общее решение относительно С_1; С₂ получаем Ci=/2(x + u + t + l)e t , С₂ = l/2(x-u + t-l)e +t . Поэтому общий интеграл этой системы суть

Следовательно, общее решение исходного уравнения задается равенством

Пример 2. Дано квазилинейное уравнение в частных производных первого порядка

Найти общее решение и решение задачи Коши г = у — — 4, х = 2.

Запишем соответствующую систему обыкновенных дифференциальных уравнений для характеристик в симметрической форме

Решая последовательно уравнение

и для уравнения получаем решение г = с₂х.

Разрешая полученные решения относительно произвольных постоянных, находим общий интеграл

Таким образом, общее решение может быть представлено в неявном виде

В данном случае мы можем записать его и в явном виде

Найдем теперь решение задачи Коши. При х = 2 должно выполняться равенство , поэтому f(s) = s.

Следовательно, z = у — х* — решение задачи Коши.

Видео:1. Уравнения в частных производных первого порядка (уравнения переноса)Скачать

ЗАДАЧИ И УПРАЖНЕНИЯ

1. Построить матричную экспоненту и матричный логарифм для матриц

2. Покажите, что любая фундаментальная матрица не вырождена.

3. Проинтегрировать системы уравнений

4. Имеет ли периодические решения система уравнений

• 5. Покажите, что все решения системы z’ = A(x)z стремятся к нулю при х—> +оо тогда и только тогда, когда все собственные числа матрицы А расположены в открытой левой комплексной полуплоскости.
• 6. Покажите, что система z’ = A(x)z имеет решения, не ограниченные при х —> +оо тогда и только тогда, когда матрица А имеет хотя бы одно собственное число с положительной вещественной частью.
• 7. Какой из следующих вариантов ответа будет верным?

Общим решением уравнения

будет

б) , где F — произвольная непрерывно дифференцируемая функция;

в) , где с₁,с₂ — произвольные постоянные.

8. Какой из следующих вариантов ответа будет верным?

Интегральной поверхностью для системы

при условии z — у при х = 0 будет:

Видео:Уравнения в частных производных первого порядка| poporyadku.schoolСкачать

Линейные дифференциальные уравнения в частных производных первого порядка

Видео:Найти общее решение уравнения в частных производных первого порядка.Скачать

Линейные однородные уравнения в частных производных первого порядка

Пусть X ₁ , X ₂ , . X_n – заданные функции переменных x ₁ , x ₂ , . x_n .

Чтобы решить линейное однородное уравнение в частных производных первого порядка:

необходимо решить систему обыкновенных дифференциальных уравнений (уравнение характеристик):
:
Далее нужно представить решение в виде:
φ ₁( x ₁ , x ₂ , . x_n ) = C ₁ ,
φ ₂( x ₁ , x ₂ , . x_n ) = C ₂ ,
.
φ_{n- 1} ( x ₁ , x ₂ , . x_n ) = C_{n- 1} ,
где C_k – постоянные.
После чего сразу получаем общее решение:
,
где F – произвольная функция от n – 1 аргументов.

Если нужно получить частное решение с определенными граничными условиями, то необходимо подставить значения переменных из граничных условий в общее решение и найти вид функции F .

Видео:Тема 4. Задача Коши для квазилинейного уравнения в частных производных первого порядкаСкачать

Линейные неоднородные уравнения в частных производных первого порядка

Пусть X ₁ , X ₂ , . X_{n+ 1} – заданные функции от переменных x ₁ , x ₂ , . x_n и z .

Чтобы решить линейное неоднородное уравнение в частных производных первого порядка:
,
необходимо решить уравнение характеристик:
.
Решение этой системы нужно представить в следующем виде:
φ ₁( x ₁ , x ₂ , . x_n , z ) = C ₁ ,
φ ₂( x ₁ , x ₂ , . x_n , z ) = C ₂ ,
.
φ_n ( x ₁ , x ₂ , . x_n , z ) = C_n .
После чего сразу получаем общий интеграл в неявном виде:

где F – произвольная функция. Также общий интеграл можно представить в различных вариантах, например:
φ ₁ = F ( φ ₂ , φ ₃ , . φ_n ) ,
φ ₂ = F ( φ ₁ , φ ₃ , . φ_n ) ,
и т. д.

Видео:Простейшие уравнения в частных производныхСкачать

Примеры решений линейных уравнений в частных производных первого порядка

Однородное уравнение

Найти общее решение линейного однородного уравнения в частных производных первого порядка и решить задачу Коши с указанным граничным условием:
,
при .

Это линейное однородное уравнение в частных производных первого порядка. Составляем уравнение характеристик:

Это уравнение характеристик содержит три уравнения:
;
;
.
Нам нужно выбрать и решить любые два из них. Тогда третье будет выполнено автоматически.

Выбираем и решаем первое уравнение:

Здесь переменные уже разделены, интегрируем:

Интегралы табличные,

Потенцируем:

Отсюда

Подставим во второе уравнение:

Или:

Это линейное уравнение. Решаем с помощью интегрирующего множителя. Умножим на x -1 и преобразуем:

Интегрируем:

Подставим полученное ранее выражение C₁ = x y 2 :

Итак, мы нашли два интеграла уравнения характеристик:

Общее решение исходного уравнения в частных производных имеет вид:

где F — произвольная функция от двух аргументов F(φ₁, φ₂) . Найдем ее вид из граничного условия
при .

Рассматриваем решение на границе.
Положим x y = –1 :

Отсюда

На границе
.

Итак, мы нашли, что на границе функция F имеет вид:
F ( φ ₁ , φ ₂ ) = φ ₁ φ ₂ .
Такой же вид она имеет и во всей области
Подставляя
;
,
получаем частное решение исходного уравнения в частных производных с заданным граничным условием:

Общее решение:

где F — произвольная функция от двух аргументов F ( φ ₁ , φ ₂ ) .

Неоднородное уравнение

Найти поверхность, удовлетворяющую данному уравнению
,
и проходящую через данную окружность x + y + z = 0 , x 2 + y 2 + z 2 = a 2 .

Это линейное неоднородное уравнение в частных производных первого порядка. Составляем уравнение характеристик:

Оно содержит три уравнения:
;
;
.
Нам нужно выбрать и решить любые два из них. Тогда третье удовлетворится автоматически. Выбираем первое и второе уравнения.

Решаем уравнение:

Умножаем на 2 z и интегрируем:

Интегралы табличные,

Потенцируем:

Отсюда
x = C ₁ y

Подставим во второе уравнение:

Или:

Замечаем, что , тогда

Это линейное уравнение. Решаем с помощью интегрирующего множителя. Разделим на y 2 и преобразуем:

Интегрируем:

Подставим полученное ранее выражение и преобразуем:

Итак, мы нашли два интеграла уравнения характеристик:

Для удобства дальнейших вычислений заметим, что функция от постоянной также является постоянной. Поэтому запишем интегралы в виде:

Общий интеграл исходного уравнения в частных производных имеет вид:
F ( φ ₁ , φ ₂) = 0
Но, поскольку F — произвольная функция от двух аргументов, то общий интеграл можно записать также в виде:
φ ₁ = F ( φ ₂) ,
где F — произвольная функция от одного аргумента.

Найдем вид этой функции, рассматривая решение на границе.
На границе, x 2 + y 2 + z 2 = a 2 , .
Из уравнения x + y + z = 0 , z = – ( x + y ) . Подставим в x 2 + y 2 + z 2 = a 2 и преобразуем:
x 2 + y 2 + ( x + y ) 2 = a 2
x 2 + y 2 + x 2 + 2 xy + y 2 = a 2
2 x 2 + 2 xy + 2 y 2 = a 2
Разделив на y 2 , имеем

Итак, мы нашли, что на границе:

.
Подставим в выражение общего интеграла:
φ ₁ = F ( φ ₂)
.
Сделаем подстановку
:
.

Итак, мы нашли, что на границе функция F имеет вид:
.
Такой же вид она имеет и во всей области, тогда
.
Подставляем выражения для φ₁ и φ₂ :

.
Умножим на a 2 y 2 .

Автор: Олег Одинцов . Опубликовано: 23-09-2014

💥 Видео

2.1. Метод характеристик. Задача Коши для гиперболического уравнения на плоскости.Скачать

Горицкий А. Ю. - Уравнения математической физики - Уравнения с частными производными 1-го порядкаСкачать

Как решать уравнения с модулем или Математический торт с кремом (часть 1) | МатематикаСкачать

Пример 65. Решить задачу Коши (диффуры)Скачать

6. Линейные однородные уравнения в частных производных первого порядкаСкачать

Задача Коши ДУ I п. 1. Caushy`s ProblemСкачать

Уравнения в частных производных 1Скачать

Лекция №7 Характеристики. Квазилинейные уравнения с частными производнымиСкачать

Приведение ДУ 2 порядка в частных производных к каноническому видуСкачать

Сергеев И. Н. - Дифференциальные уравнения II - Уравнения в частных производных первого порядкаСкачать

Лекция №13 по ДУ. Задача Коши для уравнений в частных производных 1-ого порядка. Бишаев А. М.Скачать

Тема 3. Квазилинейные, неоднородные дифференциальные уравнения в частных производных первого порядкаСкачать

Тема 5. Нелинейные уравнения в частных производных первого порядка. Метод Лагранжа-ШарпиСкачать