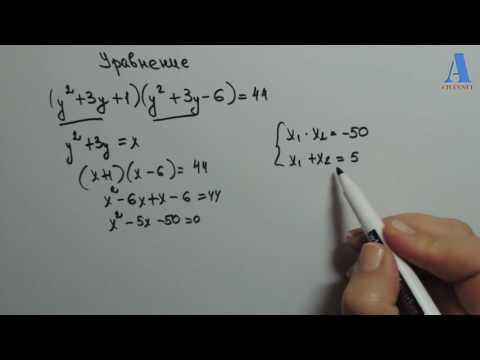- Метод замены переменной – это такой способ решения, при котором в уравнение (или неравенство) вводится новая переменная, в результате чего оно становится более простым.
- Примеры использования метода замены переменной
- Разработка урока алгебры в 8-м классе по теме «Решение уравнений методом замены переменной»
- Решение уравнений, сводящихся к квадратным
- Биквадратные уравнения
- Метод разложения на множители
- Метод замены переменной
- Выделение полного квадрата
- Примеры
- 🌟 Видео
Метод замены переменной – это такой способ решения, при котором в уравнение (или неравенство) вводится новая переменная, в результате чего оно становится более простым.
Этот метод один из самых популярных при решении сложных заданий, в частности, в ЕГЭ и ОГЭ.
У нас довольно сложное уравнение. А если раскрыть скобки, оно станет еще сложнее. Что делать? Давайте попробуем заменить переменную.
Заменим выражение (x+frac) буквой (t).
Получилось обычное квадратное уравнение! Решив его, найдем чему равно (t), после чего, сделав обратную замену, вычислим (x).
Когда не стоит вводить новую переменную? Когда это не сделает уравнение проще. Например, если старая переменная остается, несмотря на замену:
Попробуем сделать замену здесь.
Заменим выражение (sin x) буквой (t).
Видим, что в этой замене нет никакого смысла – она не упростила уравнение, даже наоборот, усложнила его, потому что теперь у нас в уравнении две переменные.
Видео:Решение уравнения методом замены переменнойСкачать
Примеры использования метода замены переменной
Заметим, что (x^4=(x^2 )^2) (см. свойства степеней ). Тогда наше уравнение приобретает следующий вид.
Теперь используем метод замены.
Вводим новую переменную, заменяя (x^2) на (t).
Мы нашли чему равно (t), но найти-то надо иксы! Поэтому делаем обратную замену.
Ответ: (±1); (±) (frac) .
Весьма частая ошибка при использовании этого метода: забыть «вернуться к иксам», то есть не сделать обратную замену. Помните – нам нужно найти (x), а не (t)! Поэтому возврат к (x) — строго обязателен!
Пример. Решить неравенство: (log^2_3x-log_3x-2>0)
Приступим к решению.
Теперь нужно вернуться к исходной переменной – иксу. Для этого перейдем к совокупности , имеющей такое же решение, и сделаем обратную замену.
Видео:решение уравнения с заменой переменнойСкачать
Разработка урока алгебры в 8-м классе по теме «Решение уравнений методом замены переменной»
Разделы: Математика
Класс: 8.
Программа: для общеобразовательных учреждений, п/р А.Г. Мордковича.
Учебник: Алгебра 8, автор А.Г. Мордкович.
Тип урока: ознакомление с новым материалом.
Цели урока: сформировать умение решать уравнения, приводимые к квадратным, путем введения новой переменной, повторить способы решения неполных квадратных уравнений, формулы сокращенного умножения
Оборудование: компьютер, мультимедийный проектор, экран, презентация к уроку, индивидуальные доски, маркеры по доске.
Раздаточный материал: карточки с заданием для самостоятельной работы.
Ход урока
1. Оргмомент.
2. Сообщение темы урока и целей урока.
— Мы должны сегодня изучить новый метод решения уравнений. Он широко применяется при решении многих типов уравнений, которые мы будем изучать в старших классах. А сегодня мы рассмотрим, как применить его при решении уравнений, которые можно свести к квадратным. Что это за способ, вы узнаете немного позже, а сейчас проверим домашнее задание.
3. Проверка домашнего задания: (Приложение 1)
4. Подготовка к изучению нового материала (работа устно).
У каждого учащегося есть индивидуальная маркерная доска, на которой он пишет ответ на задание, появляющееся на экране.
— А сейчас вспомним то, что вы изучали раньше. (Приложение 1)
Слайд 4 Решить уравнение:
х 2 = 16 2х 2 = 50
х 2 + 9 = 0 х 3 — 4х = 0
Слайд 5 Разложить на множители:
- а 2 — 36 =
- 3в 2 — 12 =
- х 2 — 10х + 25 =
- х 3 — 49х =
Раскрыть скобки:
- (х 2 + 3х ) 2 =
- (7 — х 2 ) 2 =
- — (3х — 5у ) 2 =
5. Изучение нового материала.
— Сейчас попробуйте решить это уравнение:
Слайд 6 (х 2 — 3 ) 2 + 5 (х 2 — 3 ) + 6 = 0 (Проблема)
— Как? Если, как мы обычно делали, раскрывать скобки, то получится уравнение четвертой степени (вспомните устные упражнения ), а их мы решать не умеем. Значит, надо искать другие методы. Посмотрите внимательнее на это уравнение. Ничего необычного не замечаете?
Чаще всего, дети догадываются, что в уравнении встречается повторяющееся выражение.
— Мы всегда старались все упростить. И теперь давайте попробуем это сделать: заменим выражение х 2 — 3 какой-нибудь буквой, например, t , Посмотрите, что получили?
D = b 2 — 4ac = 25 — 24 = 1
— Но мы нашли только t , нам нужно найти х. Что делать дальше ?
— Вы узнали новый метод решения уравнений, который называется » замена переменной». Это и есть тема нашего урока. Запишите. Слайд 8
— Итак, давайте попробуем сформулировать алгоритм решения уравнений методом введения новой переменной.
— Посмотрите решение еще одного примера.
— А сейчас в тетради решим подобные уравнения и поучимся оформлять их решение.
Пример 1 (3х — 4 ) 2 — 5(3х — 4 ) + 6 = 0
Сделаем замену переменной. Пусть 3х — 4 = t, получим
D = b 2 — 4ac = 25 — 24 = 1
Вернемся к замене.
1) 3х — 4 = 3
2) 3х — 4 = 2 Ответ:
; 2.
Пример 2 2(х 2 + 3 ) 2 — 7 (х 2 + 3) 2 = — 3
Сделаем замену переменной. Пусть х 2 + 3 = t, получим
D = b 2 — 4ac = 49 — 24 = 25
Вернемся к замене:
1) х 2 + 3 = 3 х = 0
2) х 2 + 3 = х 2 =
нет корней
6. Закрепление изученного материала.
— Сейчас решите из учебника № 26.22 б ; 26.23 а.в ; дополнительно 26.25.
7. Подведение итогов и задание на дом.
— Что нового вы узнали на уроке?
— Каков алгоритм решения уравнений методом замены переменной?
— Ваше домашнее задание на экране.
— На следующем уроке вы узнаете, что такое биквадратные уравнения и научитесь их решать. А сейчас проверим. как вы научились решать уравнения методом замены переменной. У каждого есть карточка с заданием. Если у вас останется время, дополнительное задание на экране. Желаю успеха!
8. Самостоятельная работа. (Приложение 2)
Вариант 1 Вариант 2 Решить уравнения: 1) (х — 5 ) 2 — 2 (х — 5 ) = 8
2) (х 2 — 8 ) 2 + 3 (х 2 — 8 ) 2 — 4 = 0
Решить уравнения: 1) (2х + 3 ) 2 — 4 (2х + 3 ) = 5
2) (х 2 + х ) 2 — 11 (х 2 + х ) = 12
Вариант 3 Вариант 4 Решить уравнения: 1) (х 2 — 2х ) 2 + (х 2 — 2х ) = 12
2) (х 2 + 2 ) 2 — 5 (х 2 + 2 ) — 6 = 0
Решить уравнения: 1) (х 2 — х ) 2 — 8 (х 2 — х ) + 12 = 0
2) (х 2 — 1 ) 2 + 2 (х 2 — 1 ) = 15
Дополнительно.
- (х 2 + 4х )( х 2 + 4х — 17 ) + 60 = 0
- (х 2 — 5х )( х 2 — 5х + 10 ) = — 24
Видео:Решение биквадратных уравнений. 8 класс.Скачать
Решение уравнений, сводящихся к квадратным
Биквадратные уравнения
Биквадратным уравнением называется уравнение вида:
$$ ax^4+bx^2+c = 0, a neq 0 $$
Алгоритм решения биквадратного уравнения
Шаг 1. Ввести новую переменную: $z = x^2 ge 0$.
Переписать уравнение для новой переменной: $az^2+bz+c = 0$
Шаг 2. Решить полученное квадратное уравнение.
Если $D gt 0$, $z_ = frac<-b pm sqrt> $. Проверить условие $z ≥ 0$, если положительных корней нет, решений нет, переход на шаг 4.
Если D = 0,$z_0 = -frac$. Проверить условие $z ge 0$, если корень отрицательный, решений нет, переход на шаг 4.
Если $D lt 0$, решений нет, переход на шаг 4.
Шаг 3.Если после шага 2 остались положительные корни, найти x: $x = pm sqrt$.
Шаг 4. Работа завершена.
Шаг 1. $z = x^2 ge 0, z^2+7z-30 = 0$
$z_1 = -10 lt 0, z_2 = 3 gt 0 $
Шаг 3. Находим корни из положительного $z: x_ = pm sqrt$
Метод разложения на множители
Решение уравнений, в которые переменная x входит с различными натуральными степенями и вещественными коэффициентами, по существу, является поиском корней многочлена.
Число $x_0$ называют корнем многочлена $P_n (x) = a_n x^n+a_ x^ + ⋯ + a_1 x+a_0$ если $P_n (x_0 ) = 0$.
Для многочлена $P_n$ (x) произвольной степени n справедливо следующее.
Если $x = x_0$ является корнем многочлена $P_n$ (x), то $P_n (x) = (x-x_0) P_ (x)$, где $P_ (x)$ — многочлен степени n-1.
Таким образом, разными способами находя корни и формируя скобки, можно постепенно добиваться понижения степени «оставшегося» многочлена, пока не будут найдены все корни.
При разложении многочлена
- множители вида (x-a) называют линейными множителями ;
- множители вида $ (x^2+bx+c)$, для которых $D lt 0$, называют неприводимыми квадратичными множителями .
Любой многочлен $P_n$ (x) можно представить в виде конечного числа линейных и/или неприводимых квадратичных множителей.
Причём, такое представление единственно с точностью до порядка множителей.
Для разложения многочленов на множители применяются разные методы:
- вынесение общего множителя за скобку (см. §19 справочника для 7 класса);
- группировка (см. §20 справочника для 7 класса);
- формулы сокращенного умножения (см. §25 справочника для 7 класса);
- метод неопределённых коэффициентов;
- выделение полного квадрата и т.п.
Решим уравнение $2x^3-x^2-8x+4 = 0$.
Раскладываем на множители: $x^2 (2x-1)-4(2x-1) = 0$
$$ (x^2-4)(2x-1) = 0 Rightarrow (x-2)(x+2)(2x-1) = 0 $$
Корни уравнения: $x_1 = 2, x_2 = -2, x_3 = frac$
Метод замены переменной
Замена переменной – это уравнение, с помощью которого можно упростить исходное уравнение, и перейти к решению системы из двух более простых уравнений:
$Исходное quad сложное quad уравнение iff <left< begin Новая quad переменная quad (урав. quad связи quad со quad старой quad переменной \ Исходное quad урав. quad в quad «упрощ.» quad виде end right.>$
Например, для биквадратных уравнений:
$$ ax^4+bx^2+c = 0 iff <left< begin z = x^2 ge 0 \ az^2+bz+c = 0 end right.> $$
Можно предложить аналогичные схемы для других уравнений:
$$ ax+b sqrt+c = 0 iff <left< begin z = sqrt ge 0 \ az^2+bz+c = 0 end right.> $$
И, в общем виде, для любой рациональной степени n:
$$ ax^+bx^n+c = 0 iff <left< begin z = x^n \ az^2+bz+c = 0 end right.> , n in Bbb Q $$
В других случаях замена переменной не настолько очевидна.
Но при удачном выборе, этот метод очень упрощает задачу.
Раскроем скобки:$ x^2-x = frac$. Сделаем замену:
$$ z = frac Rightarrow z(z-2) = 24 Rightarrow z^2-2z-24 = 0 Rightarrow (z-6)(z+4) = 0 Rightarrow left[ begin z_1 = -4 \ z_2 = 6 end right.$$
Возвращаемся к исходной переменной x:
$$ left[ begin x^2-x = -4 \ x^2-x = 6 end right. Rightarrow left[ begin x^2-x+4 = 0 \ x^2-x-6 = 0 end right. Rightarrow left[ begin D lt 0, x in varnothing \ (x-3)(x+2) = 0 end right. Rightarrow left[ begin x_1 = -2 \ x_2 = 3 end right. $$
При использовании метода замены переменной не забывайте возвращаться к исходной переменной.
Выделение полного квадрата
Метод выделения полного квадрата является одним из методов разложения на множители. Его идея – представить многочлен в виде разности квадратов двух других многочленов степенью пониже, и разложить разность на две скобки:
$$ P_n (x) = Q_k^2 (x)-R_m^2 (x) = (Q_k (x)-R_m (x))(Q_k (x)+R_m (x)) $$
Такое разложение не всегда возможно.
Рассмотрим выделение полного квадрата для квадратного трёхчлена:
$$ = a Biggl(x+frac Biggr)^2 — frac = a Biggl(x+ frac Biggr)^2- frac, D = b^2-4ac $$
Нами выделен полный квадрат $(x+frac)^2$.
Данное выражение используется для построения и анализа графиков парабол (см. §28 данного справочника).
А его разложение на две линейные скобки, известное как теорема Виета (см. §26 данного справочника), возможно только при условии $D ge 0$.
Решить уравнение $x^4+4x^2-1 = 0$
Выделим полный квадрат и разложим на множители:
$$ left[ begin x^2+2-sqrt = 0 \ x^2+2+sqrt = 0 end right. Rightarrow left[ begin x^2 = sqrt -2 gt 0 \ x^2 = -(2+sqrt) lt 0 end right. Rightarrow x_1,2 = pm sqrt<sqrt-2> $$
Примеры
Пример 1. Решите биквадратные уравнения:
Делаем замену: $2x^4+7x^2-4 = 0 iff <left< begin z = x^2 ge 0 \ 2z^2+7z-4 = 0 end right.>$
Решаем квадратное уравнение: $D = 7^2-4 cdot 2 cdot (-4) = 49+32 = 81 = 9^2$
$$ z = frac = left[ begin z_1 = -4 lt 0 \ z_2 = frac gt 0 end right. $$
Выбираем положительный z и возвращаемся к исходной переменной x:
Делаем замену: $(x+3)^4-10(x+3)^2+24 = 0 iff <left< begin z = (x+3)^2 ge 0 \ z^2-10z+24 = 0 end right.>$
Решаем квадратное уравнение: $z^2-10z+24 = 0 Rightarrow (z-4)(z-6) = 0 Rightarrow left[ begin z_1 = 4 \ z_2 = 6 end right.$
Берём оба корня и возвращаемся к исходной переменной.
$$ left[ begin (x+3)^2 = 4 \ (x+3)^2 = 6 end right. Rightarrow left[ begin x+3 = pm sqrt \ x+3 = pm sqrt end right. Rightarrow left[ begin x_ = -3 pm 2 \ x_ = -3 pm sqrt end right. Rightarrow left[ begin x_1 = -5 \ x_2 = -1 \ x_ = -3 pm sqrt end right. $$
Пример 2. Решите уравнения аналогичные биквадратным:
Делаем замену: $x+4 sqrt-60 = 0 iff <left< begin z = sqrt ge 0 \ z^2+4z-60 = 0 end right.>$
Решаем квадратное уравнение: $ z^2+4z-60 = 0 Rightarrow (z+10)(z-6) = 0 Rightarrow left[ begin z_1 = -10 \ z_2 = 6 end right.$
Выбираем положительный корень и возвращаемся к исходной переменной:
Делаем замену: $(x-1)^6-7(x-1)^3-8 = 0 iff <left< begin z = (x-1)^3 \ z^2-7z-8 = 0 end right.>$
Решаем квадратное уравнение: $ z^2-7z-8 = 0 Rightarrow (z+1)(z-8) = 0 Rightarrow left[ begin z_1 = -1 \ z_2 = 8 end right.$
При замене куба знак z может быть любым, берём оба корня и возвращаемся к исходной переменной.
$$ left[ begin (x-1)^3 = -1 \ (x-1)^3 = 8 end right. Rightarrow left[ begin x-1 = -1 \ x-1 = 2 end right. Rightarrow left[ begin x_1 = 0 \ x_2 = 3 end right. $$
Пример 3. Решите уравнения с помощью замены переменной:
Заметим, что $(x+3)^2 = x^2+6x+9$. Получаем:
$$ (x^2+6x)^2-(x^2+6x+9) = 33 Rightarrow (x^2+6x)^2-(x^2+6x)-42 = 0 $$
Решаем квадратное уравнение: $ z^2-z-42 = 0 Rightarrow (z+6)(z-7) = 0 Rightarrow left[ begin z_1 = -6 \ z_2 = 7 end right.$
Берём оба корня и возвращаемся к исходной переменной.
$$ left[ begin x^2+6x = -6 \ x^2+6x = 7 end right. Rightarrow left[ begin x^2+6x+6 = 0 \ x^2+6x-7=0 end right. Rightarrow left[ begin D = 12, x = frac<-6 pm 2 sqrt> \ (x+7)(x-1) = 0 end right. Rightarrow left[ begin x_ = -3 pm sqrt \ x_3 = -7 \ x_4 = 1 end right. $$
Делаем замену: $ frac + frac = 2 iff left[ begin z = x^2+3 ge 3 \ frac + frac = 2 end right.$
Решаем уравнение относительно z:
$$ frac + frac = 2 Rightarrow frac = frac Rightarrow 4(z+1)+5z = 2z(z+1) $$
$$ 2z^2+2z-9z-4 = 0 Rightarrow 2z^2-7z-4 = 0 $$
$$ D = 7^2-4 cdot 2 cdot (-4) = 49+32 = 81 = 9^2 $$
$$ z = frac = left[ begin z_1 = — frac lt 3 \ z_2 = 4 gt 3 end right. $$
Выбираем корень больше 3 и возвращаемся к исходной переменной:
$$ x^2+3 = 4 Rightarrow x^2 = 1 Rightarrow x_ = pm 1$$
Пример 4*. Решите уравнения:
Приведём это уравнение к биквадратному.
В линейных множителях (x+a) выберем все a =
Найдем их среднее арифметическое (см. §52 справочника для 7 класса)
Замена переменных $z = x+a_$:
Упрощаем уравнение, используя формулу разности квадратов:
$$ (z^2-9)(z^2-1) = 945 Rightarrow z^4-10z^2+9 = 945 Rightarrow z^4-10z^2-936 = 0 $$
Получили биквадратное уравнение.
Делаем замену: $z^4-10z^2-936 = 0 iff <left< begin t = z^2 ge 0 \ t^2-10t-936 = 0 end right.> $
Решаем квадратное уравнение:
$$ D = 100+4 cdot 936 = 3844 = 62^2, t = frac = left[ begin t_1 = -26 lt 0 \ t_2 = 36 gt 0 end right. $$
Выбираем положительный корень и возвращаемся к переменной z:
$$ z = pm sqrt = pm sqrt = pm 6 $$
Возвращаемся к исходной переменной x:
$$ x = z-4 = pm 6-4 = left[ begin x_1 = -10 \ x_2 = 2 end right. $$
$$ z- frac =2,1 |times z (z neq 0) $$
$$ z^2-2,1z-1 = 0 Rightarrow D = 2,1^2+4 = 8,41 = 2,9^2; z = frac = left[ begin z_1 = -0,4 \ z_2 = 2,5 end right. $$
Берём оба корня и возвращаемся к исходной переменной.
$$ left[ begin frac = -0,4 \ frac = 2,5 end right. Rightarrow left[ begin x^2+1 = -0,4x \x^2+1 = 2,5x end right. Rightarrow left[ begin x^2+0,4x+1 = 0 \ x^2-2,5x+1 = 0 end right. $$
В первом уравнении $D = 0,4^2-4 lt 0$, решений нет.
Во втором уравнении (x-2)(x-1/2) = 0 $Rightarrow left[ begin x_1 = frac \ x_2 = 2 end right.$
🌟 Видео
Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать
Решение квадратных уравнений. Метод разложения на множители. 8 класс.Скачать
Решение квадратного уравнения методом замены переменнойСкачать
Решение задач с помощью квадратных уравнений. Алгебра, 8 классСкачать
9 класс. Алгебра. Решение уравнений методом замены переменной.Скачать
Алгебра Система уравнений Метод замены переменной № 6.22 9 классСкачать
Решение уравнений методом замены переменной.Скачать
Решение квадратных неравенств | МатематикаСкачать
8 класс "Решение уравнений методом замены переменной"Скачать
Алгебра 9 класс. Решение систем уравнений методом замены переменныхСкачать
Решение квадратных уравнений. Дискриминант. 8 класс.Скачать
10 класс, 23 урок, Методы решения тригонометрических уравненийСкачать
Математика | Система уравнений на желтую звездочку (feat Золотой Медалист по бегу)Скачать
Быстрый способ решения квадратного уравненияСкачать
#134 Урок 59. Замена переменной. Решение уравнений, приводящихся к квадратным. Алгебра 8 класс.Скачать
9 класс. Алгебра. Решение уравнений. Замена переменной.Скачать
; 2.
