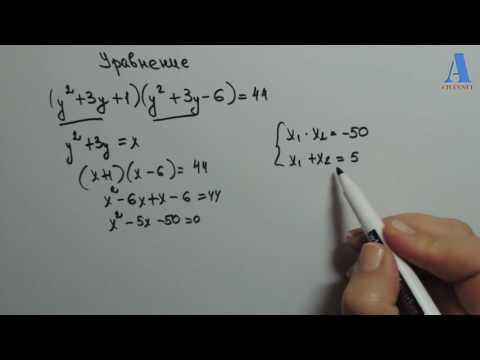Решение квадратных уравнений способом введения новой переменной

В этой статье мы всесторонне разберем метод введения новой переменной. Здесь мы выясним, для решения каких уравнений этот метод предназначен, проникнем в его суть, приведем обоснование метода, доказав соответствующее утверждение, запишем алгоритм решения уравнений методом введения новой переменной и рассмотрим решения характерных примеров.

Видео:Решение биквадратных уравнений. 8 класс.Скачать

Когда применяется и в чем суть метода

Метод введения новой переменной предназначен для решения уравнений, имеющих вид f(g(x))=0 или f₁(g(x))=f₂(g(x)) , где f , f₁ и f₂ – некоторые функции, а x – неизвестная переменная. Для лучшего восприятия приведем примеры таких уравнений:

• (x 2 ) 3 −3·x 2 +2=0 , это уравнение имеет вид f(g(x))=0 , здесь g(x)=x 2 , а функция f такая, что f(t)=t 2 −3·t+2 ;
• , это уравнение вида f₁(g(x))=f₂(g(x)) , здесь в качестве g(x) можно рассматривать x 2 +2·x , тогда функции f₁ и f₂ таковы, что и ;
• , это уравнение, имеющее вид f(g(x))=0 , где , а функция f описывается как .

Понятно, что f(g(x))=0 и f₁(g(x))=f₂(g(x)) — равносильные уравнения, так как уравнение f₁(g(x))=f₂(g(x)) приводится к виду f(g(x))=0 при помощи равносильного преобразования, заключающегося в переносе выражения f₂(g(x)) из правой части в левую с противоположным знаком. Поэтому дальнейшую теорию мы будем излагать только для уравнений вида f(g(x))=0 , это сделано в угоду краткости без ущерба для общности.

Суть метода введения новой переменной для решения уравнения f(g(x))=0 состоит во введении новой переменной t как g(x)=t с целью нахождения всех корней исходного уравнения через множество решений T уравнения f(t)=0 с новой переменной t и использование равенства g(x)=t . Забегая немного вперед, скажем, что корнями исходного уравнения являются все такие значения x , которые удовлетворяют условию g(x)∈T . В частности,

• если T – пустое множество, то есть, уравнение f(t)=0 не имеет решений, то условие g(x)∈T определяет пустое множество, а это означает, что исходное уравнение не имеет решений;
• если T – конечное множество, то есть, уравнение f(t)=0 имеет n решений t₁, t₂, …, t_n , то условие g(x)∈T есть не что иное, как совокупность уравнений g(x)=t₁, g(x)=t₂, …, g(x)=t_n , а это означает, что решением исходного уравнения является решение совокупности уравнений g(x)=t₁, g(x)=t₂, …, g(x)=t_n .

Поясним на примере. Возьмем уже упомянутое выше уравнение (x 2 ) 3 −3·x 2 +2=0 . Введение новой переменной x 2 =t позволяет от исходного уравнения перейти к кубическому уравнению t 3 −3·t+2=0 с новой переменной (заменяем в исходном уравнении x 2 на t ). Множество решений этого уравнения T (оно в нашем случае состоит из двух чисел t₁=1 и t₂=−2 , то есть, T= ) и использование равенства x 2 =t дают возможность определить все корни исходного уравнения. Они определяются по условию x 2 ∈ , которое есть не что иное, как совокупность двух уравнений x 2 =−2 , x 2 =1 .

В основе метода введения новой переменной лежит следующее утверждение:

Решение уравнения f(g(x))=0 есть множество значений переменной x , удовлетворяющих условию g(x)∈T , где T – множество всех корней уравнения f(t)=0 .

Приведем обоснование озвученного утверждения в следующем пункте.

Видео:§101 Метод введения новой переменнойСкачать

Обоснование

Докажем утверждение, лежащее в основе метода введения новой переменной, которое мы привели в предыдущем пункте. Для этого нужно доказать два момента:

• что любой корень уравнения f(g(x))=0 удовлетворяет условию g(x)∈T , где T – множество всех корней уравнения f(t)=0 ,
• что любое значение переменной x , удовлетворяющее условию g(x)∈T , где T – множество всех корней уравнения f(t)=0 , является корнем уравнения f(g(x))=0 .

Начнем с первой части. Пусть x₀ – корень уравнения f(g(x))=0 . Докажем, что x₀ удовлетворяет условию g(x)∈T , где T – множество всех корней уравнения f(t)=0 .

Так как x₀ – корень уравнения f(g(x))=0 , то f(g(x₀))=0 – верное числовое равенство. Из этого равенства следует, что g(x₀) – корень уравнения f(t)=0 . А из этого следует, что g(x₀) принадлежит множеству всех корней уравнения f(t)=0 .

Первая часть доказана. Переходим к доказательству второй части утверждения.

Пусть x₀ удовлетворяет условию g(x)∈T , где T – множество всех корней уравнения f(t)=0 . Докажем, что x₀ является корнем уравнения f(g(x))=0 .

Так как x₀ удовлетворяет условию g(x)∈T , то g(x₀)∈T , то есть, g(x₀) – это один из корней уравнения f(t)=0 . Значит, f(g(x₀))=0 – верное числовое равенство. А из этого равенства следует, что x₀ – корень уравнения f(g(x))=0 .

Так доказана вторая часть утверждения и все утверждение в целом.

Видео:Решение уравнения методом замены переменнойСкачать

Алгоритм решения уравнений методом введения новой переменной

Приведенная выше информация позволяет записать алгоритм решения уравнения f(g(x))=0 методом введения новой переменной:

• Вводится новая переменная t как g(x)=t , и осуществляется переход от исходного уравнения f(g(x))=0 со старой переменной x к уравнению f(t)=0 с новой переменной t .
• Решается полученное уравнение с новой переменной. При этом
  • если оно не имеет корней, то делается вывод об отсутствии корней у исходного уравнения,
  • если уравнение имеет корни, то выполняются следующие шаги алгоритма.
• Осуществляется возврат к старой переменной. Для этого
  • если решенное на предыдущем шаге уравнение имеет единственный корень, обозначим его t₁ , то составляется уравнение g(x)=t₁ ,
  • если решенное на предыдущем шаге уравнение имеет два, три или любое другое, но конечное число корней, обозначим их t₁, t₂, …, t_n , то составляется совокупность уравнений g(x)=t₁, g(x)=t₂, …, g(x)=t_n ,
  • если же решенное на предыдущем шаге уравнение имеет бесконечно много корней, и они составляют числовое множество T , то составляется совокупность уравнений, неравенств и двойных неравенств, отвечающая выражению g(x)∈T (например, если решением уравнения с новой переменной t является числовое множество (−∞, t₁)∪<t₂>∪[t₃, t₄) , что то же самое , то соответствующая совокупность будет иметь вид ).
• Наконец, решается составленное уравнение или совокупность – ее решение есть искомое решение исходного уравнения.

Видео:Решение рациональных уравнений методом введения новой переменной | Алгебра 8 класс #37 | ИнфоурокСкачать

Решение примеров

Обычно первое знакомство с методом введения новой переменной происходит в школе в рамках темы «решение рациональных уравнений». В частности, рациональными являются биквадратные уравнения, стандартным методом решения которых как раз является метод введения новой переменной. Для примера приведем краткое решение методом введения новой переменной биквадратного уравнения x 4 −3·x 2 +5=0 . После представления его в виде (x 2 ) 2 −3·x 2 +5=0 , вводим новую переменную x 2 =t , это позволяет перейти к квадратному уравнению с новой переменной: t 2 −3·t+5=0 . Оно не имеет действительных корней, так как его дискриминант D=(−3) 2 −4·1·5=−11 – отрицательный, откуда заключаем, что исходное уравнение не имеет корней.

Среди рациональных уравнений масса и других типичных представителей, решающихся методом введения новой переменной. Такими, во-первых, являются уравнения, в которых переменная фигурирует только в одинаковых квадратных двучленах, например (x 2 −5·x+4)·(x 2 −5·x+6)=120 , (x 2 +5) 2 −11·(x 2 +5)+28=0 , . Во-вторых, через введение новой переменной решаются уравнения, в которых переменная находится только во взаимно обратных дробях, например, , здесь одна из дробей принимается за t , а другая, очевидно, выражается через t как 1/t , ведь на ОДЗ для данного уравнения . В-третьих, упомянем про возвратные уравнения, которые тоже решаются методом введения новой переменной, а именно . Решения подобных уравнений Вы без труда найдете в статье, упомянутой в первом предложении этого пункта, а также на страницах школьных учебников, например, [1, c. 74-75, 80; 2, с. 150-152; 3, с. 213-216].

Продвигаясь дальше в школьном курсе математики по пути знакомства с уравнениями, нам встречаются иррациональные, тригонометрические, показательные, логарифмические и другие уравнения, и каждый раз мы возвращаемся к методу введения новой переменной для их решения. Для уравнений каждого вида есть свои особенности в плане введения новой переменной. Рекомендуем ознакомиться с ними в следующих материалах:

• решение иррациональных уравнений методом введения новой переменной,
• метод введения новой переменной при решении показательных уравнений,
• решение показательных уравнений методом введения новой переменной,
• решение тригонометрических уравнений методом введения новой переменной.

В заключение покажем пример решения уравнения, которое после введения новой переменной имеет бесконечное множество решений. Подобные случаи встречаются крайне редко, и тем они еще более интересны. В них главное разобраться с особенностями возврата к старой переменной.

Решите уравнение

Видео:Решение уравнений методом введения новой переменнойСкачать

Решение уравнения методом введения новой переменной

Математика. Уравнения. 283гр. Дистанционное обучение.

Просмотр содержимого документа
«Решение уравнения методом введения новой переменной»

21.04.20. Задание: Записать конспект и решить уравнения

Тема: Основные приемы решения уравнений:

Решение уравнения методом введения новой переменной

Метод введения новой переменной:

1. в уравнении какая-то его часть заменяется другой переменной (a, y, t. )

(прежнее неизвестное одновременно с новым в уравнении быть не может);

2. решается новое уравнение;

3. возвращаются к обозначенному и, используя полученное число (корни), вычисляют требуемое неизвестное.

Пример: Решить уравнение (2x−21) 2 −5(2x−21)+4=0.

Это уравнение можно решить и без использования новой переменной (раскрываются скобки по формуле разности квадратов и т. д.), но решение будет длинным и с большими числами.

Используем то, что обе скобки равны.

Обозначаем 2x−21=y. Получается простое квадратное уравнение:

D=b 2 -4ac=(-5) 2 -4•1•4=25-16=9

Возвращаемся к обозначенному:

Методом введения новой переменной решаются биквадратные уравнения:

ax 4 +bx 2 +c=0, где a,b,c ∈R; x 2 =y; ay 2 +by+c=0. В биквадратных уравнениях всегда используется новая переменная. Получается квадратное уравнение

Пример: Решить уравнение:

x 4 −13x 2 +12=0; x 2 =y, тогда

1)x 2 =12; или 2) x 2 =1,

Задание: Решить уравнения 1. (3x−4) 2 +3 (3x−4)-4=0.

Видео:Квадратные уравнения. Метод введения новой переменнойСкачать

Разработка урока алгебры в 8-м классе по теме «Решение уравнений методом замены переменной»

Разделы: Математика

Класс: 8.

Программа: для общеобразовательных учреждений, п/р А.Г. Мордковича.

Учебник: Алгебра 8, автор А.Г. Мордкович.

Тип урока: ознакомление с новым материалом.

Цели урока: сформировать умение решать уравнения, приводимые к квадратным, путем введения новой переменной, повторить способы решения неполных квадратных уравнений, формулы сокращенного умножения

Оборудование: компьютер, мультимедийный проектор, экран, презентация к уроку, индивидуальные доски, маркеры по доске.

Раздаточный материал: карточки с заданием для самостоятельной работы.

Ход урока

1. Оргмомент.

2. Сообщение темы урока и целей урока.

— Мы должны сегодня изучить новый метод решения уравнений. Он широко применяется при решении многих типов уравнений, которые мы будем изучать в старших классах. А сегодня мы рассмотрим, как применить его при решении уравнений, которые можно свести к квадратным. Что это за способ, вы узнаете немного позже, а сейчас проверим домашнее задание.

3. Проверка домашнего задания: (Приложение 1)

4. Подготовка к изучению нового материала (работа устно).

У каждого учащегося есть индивидуальная маркерная доска, на которой он пишет ответ на задание, появляющееся на экране.

— А сейчас вспомним то, что вы изучали раньше. (Приложение 1)

Слайд 4 Решить уравнение:

х 2 = 16 2х 2 = 50

х 2 + 9 = 0 х 3 — 4х = 0

Слайд 5 Разложить на множители:

1. а 2 — 36 =
2. 3в 2 — 12 =
3. х 2 — 10х + 25 =
4. х 3 — 49х =

Раскрыть скобки:

1. (х 2 + 3х ) 2 =
2. (7 — х 2 ) 2 =
3. — (3х — 5у ) 2 =

5. Изучение нового материала.

— Сейчас попробуйте решить это уравнение:

Слайд 6 (х 2 — 3 ) 2 + 5 (х 2 — 3 ) + 6 = 0 (Проблема)

— Как? Если, как мы обычно делали, раскрывать скобки, то получится уравнение четвертой степени (вспомните устные упражнения ), а их мы решать не умеем. Значит, надо искать другие методы. Посмотрите внимательнее на это уравнение. Ничего необычного не замечаете?

Чаще всего, дети догадываются, что в уравнении встречается повторяющееся выражение.

— Мы всегда старались все упростить. И теперь давайте попробуем это сделать: заменим выражение х 2 — 3 какой-нибудь буквой, например, t , Посмотрите, что получили?

D = b 2 — 4ac = 25 — 24 = 1

— Но мы нашли только t , нам нужно найти х. Что делать дальше ?

— Вы узнали новый метод решения уравнений, который называется » замена переменной». Это и есть тема нашего урока. Запишите. Слайд 8

— Итак, давайте попробуем сформулировать алгоритм решения уравнений методом введения новой переменной.

— Посмотрите решение еще одного примера.

— А сейчас в тетради решим подобные уравнения и поучимся оформлять их решение.

Пример 1 (3х — 4 ) 2 — 5(3х — 4 ) + 6 = 0

Сделаем замену переменной. Пусть 3х — 4 = t, получим

D = b 2 — 4ac = 25 — 24 = 1

Вернемся к замене.

1) 3х — 4 = 3

2) 3х — 4 = 2 Ответ: ; 2. Пример 2 2(х 2 + 3 ) 2 — 7 (х 2 + 3) 2 = — 3 Сделаем замену переменной. Пусть х 2 + 3 = t, получим D = b 2 — 4ac = 49 — 24 = 25 Вернемся к замене: 1) х 2 + 3 = 3 х = 0 2) х 2 + 3 = х 2 = нет корней 6. Закрепление изученного материала. — Сейчас решите из учебника № 26.22 б ; 26.23 а.в ; дополнительно 26.25. 7. Подведение итогов и задание на дом. — Что нового вы узнали на уроке? — Каков алгоритм решения уравнений методом замены переменной? — Ваше домашнее задание на экране. — На следующем уроке вы узнаете, что такое биквадратные уравнения и научитесь их решать. А сейчас проверим. как вы научились решать уравнения методом замены переменной. У каждого есть карточка с заданием. Если у вас останется время, дополнительное задание на экране. Желаю успеха! 8. Самостоятельная работа. (Приложение 2) Вариант 1 Вариант 2 Решить уравнения: 1) (х — 5 ) 2 — 2 (х — 5 ) = 8 2) (х 2 — 8 ) 2 + 3 (х 2 — 8 ) 2 — 4 = 0 Решить уравнения: 1) (2х + 3 ) 2 — 4 (2х + 3 ) = 5 2) (х 2 + х ) 2 — 11 (х 2 + х ) = 12 Вариант 3 Вариант 4 Решить уравнения: 1) (х 2 — 2х ) 2 + (х 2 — 2х ) = 12 2) (х 2 + 2 ) 2 — 5 (х 2 + 2 ) — 6 = 0 Решить уравнения: 1) (х 2 — х ) 2 — 8 (х 2 — х ) + 12 = 0 2) (х 2 — 1 ) 2 + 2 (х 2 — 1 ) = 15 Дополнительно. (х 2 + 4х )( х 2 + 4х — 17 ) + 60 = 0 (х 2 — 5х )( х 2 — 5х + 10 ) = — 24 🎥 Видео Алгебра Система уравнений Метод замены переменной № 6.22 9 классСкачать Решение квадратных уравнений. Метод разложения на множители. 8 класс.Скачать Быстрый способ решения квадратного уравненияСкачать Алгебра 9 класс. Решение систем уравнений методом замены переменныхСкачать Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать 9 класс, 11 урок, Методы решения систем уравненийСкачать Решение квадратных уравнений. Дискриминант. 8 класс.Скачать Решение показательных уравнений способом введения новой переменнойСкачать решение уравнения с заменой переменнойСкачать Квадратные уравнения от «А» до «Я». Классификация, решение и теорема Виета | МатематикаСкачать 5 способов решения квадратного уравнения ➜ Как решать квадратные уравнения?Скачать Неполные квадратные уравнения. Алгебра, 8 классСкачать Решение показательных уравнений методом введения новой переменной. Подготовка к ГВЭ11 + ЕГЭ 2021 #70Скачать Решение биквадратных уравнений. Практическая часть. 2ч. 8 класс.Скачать Поделиться или сохранить к себе: Смотрите также Сера — химические свойства, получение, соединения. Нитрат кальция: способы получения и химические свойства Кальций: способы получения и химические свойства Гидроксид натрия: способы получения и химические свойства Гидроксид кальция: способы получения и химические свойства Получение бензола Разница между глюкозой и сахарозой Гидроксид калия: способы получения и химические свойства