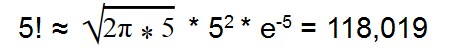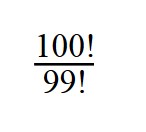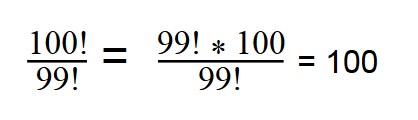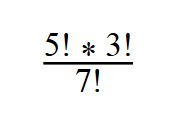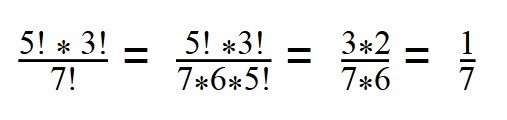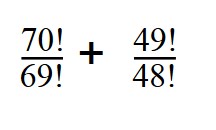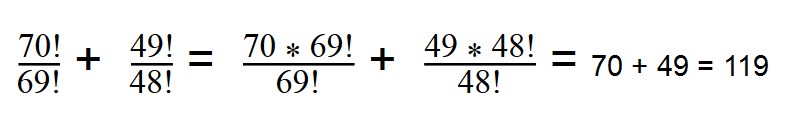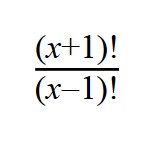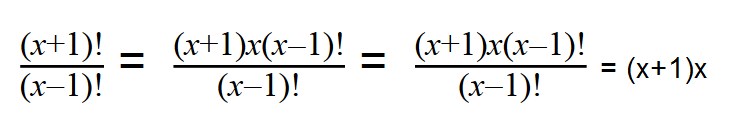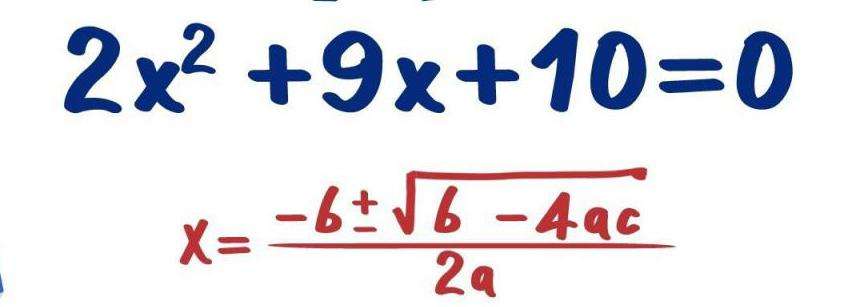Применение уравнений широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Уравнения человек использовал еще в древности и с тех пор их применение только возрастает. Факториалом n! называется произведение n последовательных натуральных чисел, начиная с единицы:
[n! = 1cdot2cdot3(n-1) cdot n]
Факториал нуля равен единице:
Так же используются факториалы по четным и нечетным числам. Обозначаются они следующим образом:
[ (2n)!! = 2cdot4cdot6ldots(2n — 2)( 2n) ] (1)
[ (2n + 1)!!] — факториал по всем нечетным числам до [(2n +1) ]
Факториал — частое явление в комбинаторике, поэтому знание их способов решения очень важно.
Допустим, дано уравнение с факториалом следующего вида:
Для решения данного дробного уравнения с факториалом необходимо вынести за пределы скобок 6!:
Решим дробное уравнение с двойным факториалом следующего вида:
Из вышеописанного равенства (1) следует:
Как видите, уравнения с факториалами довольно легко решаются с помощью несложных преобразований и арифметических операций, главное знать алгоритм их решения и формулы преобразования.
- Где можно решить уравнение с факториалом онлайн?
- Факториал
- Факториал: определение
- Формулы и свойства факториала
- Примеры решений
- Методы решения квадратных уравнений. Формула Виета для квадратного уравнения
- Какое уравнение называется квадратным
- Какие методы решения уравнений квадратных существуют
- Метод №1. Разложение на множители
- Пример решения методом факторизации
- Метод №2. Дополнение до полного квадрата
- Пример решения с помощью дополнения до полного квадрата
- Метод №3. Применение известной формулы
- Теорема Виета
- Пример использования теоремы Виета
- 🎥 Видео
Видео:5 способов решения квадратного уравнения ➜ Как решать квадратные уравнения?Скачать
Где можно решить уравнение с факториалом онлайн?
Решить уравнение вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить уравнение онлайн любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как решить уравнение на нашем сайте. А если у вас остались вопросы, то вы можете задать их в нашей групе Вконтакте http://vk.com/pocketteacher. Вступайте в нашу группу, мы всегда рады помочь вам.
Наш искусственный интеллект решает сложные математические задания за секунды.
Мы решим вам контрольные, домашние задания, олимпиадные задачи с подробными шагами. Останется только переписать в тетрадь!
Видео:Как решить уравнение с факториалами | Подходы и методы решенияСкачать
Факториал
О чем эта статья:
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Видео:Решение квадратных уравнений. Дискриминант. 8 класс.Скачать
Факториал: определение
Факториал числа n — это произведение натуральных чисел от 1 до n. Обозначается n, произносится «эн-факториал».
Факториал определен для целых неотрицательных чисел. Это значит, что вот так нельзя:
Число должно быть целое и положительное:
- 3! 56! 12!
| Формула факториала n!=1⋅2⋅3⋅. ⋅(n−2)⋅(n−1)⋅n |
Вычисляется факториал по формуле: путем умножения всех чисел от одного до значения самого числа под факториалом. Факторизация — это разложение функции на множители.
Мы видим, что 4! — это 3!*4
5! — это 4!*5
6! — это 5!*6
Видео:Решите уравнение ➜ ДВИ до ЕГЭСкачать
Формулы и свойства факториала
Чтобы узнать, как вычислять факториалы быстро — воспользуемся табличкой. Сохраняйте себе и решайте раньше остальных.
| 1! = 1 |
| 2! = 2 |
| 3! = 6 |
| 4! = 24 |
| 5! = 120 |
| 6! = 720 |
| 7! = 5040 |
| 8! = 40320 |
| 9! = 362880 |
| 10! = 3628800 |
| 11! = 39916800 |
| 12! = 479001600 |
| 13! = 6227020800 |
| 14! = 87178291200 |
| 15! = 1307674368000 |
| 16! = 20922789888000 |
| 17! = 355687428096000 |
| 18! = 6402373705728000 |
| 19! = 121645100408832000 |
| 20! = 2432902008176640000 |
| 21! = 51090942171709440000 |
| 22! = 1124000727777607680000 |
| 23! = 25852016738884976640000 |
| 24! = 620448401733239439360000 |
| 25! = 15511210043330985984000000 |
Факториалов в математике 9 класса — полно. Чтобы всегда быть готовым решить пример, запомните основные формулы:
- (n — 1)! = 1*2*3*4*5*. *(n — 2)(n — 1)
- n! = 1*2*3*4*5*. *(n — 2)(n — 1)n
- (n + 1)! = 1*2*3*4*5*. *(n — 2)(n — 1)n(n + 1)
С помощью формулы Стирлинга можно вычислить факториал многоразрядных чисел.
Такая формула дает результат с небольшой погрешностью.
 |
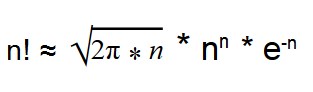Рекуррентная формула
 |
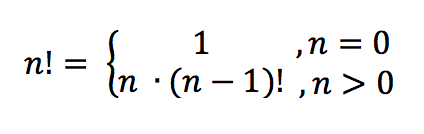- 5! = 5*(5 — 1)! = 5*4! = 5*24 = 120
- 6! = 6*(6-1)! = 6*5! = 6*120 = 720
Для решения примеров обращайтесь к таблице.
Примеры умножения факториалов:
- Пользуйтесь готовой таблицей 5! * 7! = 120 * 5040 = 604800
- Или раскладывайте факториалы отдельно, если хотите потренироваться:
5! = 1*2*3*4*5 = 4! * 5 =120
7! = 1*2*3*4*5*6*7 = 6! * 7 = 5040
120 * 5040 = 604800
Нужно быстро привести знания в порядок перед экзаменом? Записывайтесь на курсы ЕГЭ по математике в Skysmart!
Видео:Как решать квадратные уравнения. 8 класс. Вебинар | МатематикаСкачать
Примеры решений
Давайте поупражняемся и решим пару примеров.
1. Сократите дробь:
При сокращении факториалов, пользуйтесь свойством:
n! = (n — 1)! * n
100! = 99! * 100
Далее сокращаем по принципу сокращения обыкновенных дробей.
2. Вычислите значение выражения с факториалом: 8! + 5!
Можно для решения факториалов воспользоваться таблицей и вычислить быстрее.
А можно потренироваться и разложить их:
8! = 1*2*3*4*5*6*7*8 = 7!*8 = 5040 * 8 = 40320
5! = 1*2*3*4*5 = 4!*5 = 120
40320 + 120 = 40440
8! + 5! = 40440
3. Вычислите значение выражения:
7! = 1*2*3*4*5*6*7 = 5! * 6 *7
Далее сокращаем все, что можем сократить (3*2=6, сокращаем числа 6) и получаем ответ.
4. Вычислите значение выражение:
Вы уже знаете, как найти факториал — раскладываем 70 и 49:
70! = 1*2*3*. *69 = 69! * 70
49! = 1*2*3*. 49! * 48
Далее сокращаем все одинаковые множители.
5. Сократите дробь:
Проводим разложение на множители при помощи формул сокращенного умножения (x+1)x(x-1) и сокращаем все одинаковые множители (x-1)!.
Если вы все еще считаете, что факториал бесполезен и не может помочь вам в жизни, то это не так. Он помогает легко вычислять вероятности (а это бывает нужно чаще, чем кажется). К тому же, комбинаторика необходима тем, кто собирается работать в IT. Поэтому решайте побольше задачек на факториалы, в мире будущего без них — никуда.
Видео:Быстрый способ решения квадратного уравненияСкачать
Методы решения квадратных уравнений. Формула Виета для квадратного уравнения
Квадратные уравнения часто появляются в ряде задач по математике и физике, поэтому уметь их решать должен каждый школьник. В этой статье подробно рассматриваются основные методы решения уравнений квадратных, а также приводятся примеры их использования.
Видео:Решите уравнение c факториаламиСкачать
Какое уравнение называется квадратным
В первую очередь ответим на вопрос этого пункта, чтобы лучше понимать, о чем пойдет речь в статье. Итак, уравнение квадратное имеет следующий общий вид: c + b*x+a*x2=0, где a, b, c — некоторые числа, которые называются коэффициентами. Здесь a≠0 — это обязательное условие, в противном случае указанное уравнение вырождается в линейное. Остальные коэффициенты (b, c) могут принимать абсолютно любые значения, включая ноль. Так, выражения типа a*x2=0, где b=0 и c=0 или c+a*x2=0,где b=0, или b*x+a*x2=0, где c=0 — это тоже уравнения квадратные, которые называют неполными, поскольку в них либо линейный коэффициент b равен нулю, либо нулевым является свободный член c, либо они оба зануляются.
Вам будет интересно: Химические цепочки превращений: примеры и способы решения
Уравнение, в котором a=1, называют приведенным, то есть оно вид имеет: x2 + с/a + (b/a)*x =0.
Решение квадратного уравнения заключается в нахождении таких значений x, которые удовлетворяют его равенству. Эти значения называются корнями. Поскольку рассматриваемое уравнение — это выражение второй степени, то это означает, что максимальное число его корней не может превышать двух.
Видео:Квадратные уравнения от «А» до «Я». Классификация, решение и теорема Виета | МатематикаСкачать
Какие методы решения уравнений квадратных существуют
В общем случае существует 4 метода решения. Ниже перечисляются их названия:
Вам будет интересно: Каково значение слова «транспарентность»?
Как понятно из приведенного списка, первые три метода являются алгебраическими, поэтому они используются чаще, чем последний, который предполагает построение графика функции.
Существует еще один способ решения по теореме Виета уравнений квадратных. Его можно было бы включить 5-м в список выше, однако, это не сделано, поскольку теорема Виета является простым следствием 3-го метода.
Далее в статье рассмотрим подробнее названные способы решения, а также приведем примеры их использования для нахождения корней конкретных уравнений.
Видео:ФакториалСкачать
Метод №1. Разложение на множители
Для этого метода в математике квадратных уравнений существует красивое название: факторизация. Суть этого способа заключается в следующем: необходимо квадратное уравнение представить в виде произведения двух членов (выражений), которое должно равняться нулю. После такого представления можно воспользоваться свойством произведения, которое будет равно нулю только тогда, когда один или несколько (все) его членов являются нулевыми.
Теперь рассмотрим последовательность конкретных действий, которые нужно выполнить, чтобы найти корни уравнения:
Вам будет интересно: Коммуникативная методика обучения английскому языку: главные принципы, учебники, результаты, отзывы
Как видно, алгоритм факторизации является достаточно простым, тем не менее, у большинства школьников возникают трудности во время реализации 2-го пункта, поэтому поясним его подробнее.
Чтобы догадаться, какие 2-а линейных выражения при умножении их друг на друга дадут искомое квадратное уравнение, необходимо запомнить два простых правила:
- Линейные коэффициенты двух линейных выражений при умножении их друг на друга должны давать первый коэффициент квадратного уравнения, то есть число a.
- Свободные члены линейных выражений при их произведении должны давать число c искомого уравнения.
После того, как подобраны все числа множителей, следует выполнить их перемножение, и если они дают искомое уравнение, тогда переходить к пункту 3 в изложенном выше алгоритме, в противном случае следует изменить множители, но делать это нужно так, чтобы приведенные правила всегда выполнялись.
Видео:Факториалы - быстрое вычисление | Профильная математикаСкачать
Пример решения методом факторизации
Покажем наглядно, как алгоритм решения уравнения квадратного составить и найти неизвестные корни. Пусть дано произвольное выражение, например, 2*x-5+5*x2-2*x2 = x2+2+x2+1. Перейдем к его решению, соблюдая последовательность пунктов от 1-го до 3-х, которые изложены в предыдущем пункте статьи.
Пункт 1. Перенесем все члены в левую часть и выстроим их в классической последовательности для квадратного уравнения. Имеем следующее равенство: 2*x+(-8)+x2=0.
Пункт 2. Разбиваем на произведение линейных уравнений. Поскольку a=1, а с=-8, то подберем, например, такое произведение (x-2)*(x+4). Оно удовлетворяет изложенным в пункте выше правилам поиска предполагаемых множителей. Если раскрыть скобки, то получим: -8+2*x+x2, то есть получается точно такое же выражение, как в левой части уравнения. Это означает, что мы правильно угадали множители, и можно переходить к 3-му пункту алгоритма.
Пункт 3. Приравниваем каждый множитель нулю, получаем: x=-4 и x=2.
Если возникают какие-либо сомнения в полученном результате, то рекомендуется выполнить проверку, подставляя найденные корни в исходное уравнение. В данном случае имеем: 2*2+22-8=0 и 2*(-4)+(-4)2-8=0. Корни найдены правильно.
Таким образом, методом факторизации мы нашли, что заданное уравнение два корня различных имеет: 2 и -4.
Видео:Решение задач с помощью квадратных уравнений. Алгебра, 8 классСкачать
Метод №2. Дополнение до полного квадрата
В алгебре уравнений квадратных метод множителей не всегда может использоваться, поскольку в случае дробных значений коэффициентов квадратного уравнения возникают сложности в реализации пункта 2 алгоритма.
Метод полного квадрата, в свою очередь, является универсальным и может применяться для квадратных уравнений любого типа. Суть его заключается в выполнении следующих операций:
Описанный алгоритм может на первый взгляд быть воспринят, как достаточно сложный, однако, на практике его реализовать проще, чем метод факторизации.
Видео:Решение квадратных уравнений. Дискриминант. Практическая часть. 1ч. 8 класс.Скачать
Пример решения с помощью дополнения до полного квадрата
Приведем пример уравнения квадратного для тренировки его решения методом изложенным в предыдущем пункте. Пусть дано уравнение квадратное -10 — 6*x+5*x2 = 0. Начинаем решать его, следуя описанному выше алгоритму.
Пункт 1. Используем метод переброски при решении уравнений квадратных, получаем: — 6*x+5*x2 = 10.
Пункт 2. Приведенный вид этого уравнения получается путем деления на число 5 каждого его члена (если равенства обе части поделить или умножить на одинаковое число, то равенство сохранится). В результате преобразований получим: x2 — 6/5*x = 2.
Пункт 3. Половина от коэффициента — 6/5 равна -6/10 = -3/5, используем это число для составления полного квадрата, получаем: (-3/5+x)2. Раскроем его и полученный свободный член следует вычесть из части равенства левой, чтобы удовлетворить исходному виду квадратного уравнения, что эквивалентно его добавлению в правую часть. В итоге получаем: (-3/5+x)2 = 59/25.
Пункт 4. Вычисляем квадратный корень с положительным и отрицательным знаками и находим корни: x = 3/5±√59/5 = (3±√59)/5. Два найденных корня имеют значения: x1 = (√59+3)/5 и x1 = (3-√59)/5.
Поскольку проведенные вычисления связаны с корнями, то велика вероятность допустить ошибку. Поэтому рекомендуется проверить правильность корней x2 и x1. Получаем для x1: 5*((3+√59)/5)2-6*(3+√59)/5 — 10 = (9+59+6*√59)/5 — 18/5 — 6*√59/5-10 = 68/5-68/5 = 0. Подставляем теперь x2: 5*((3-√59)/5)2-6*(3-√59)/5 — 10 = (9+59-6*√59)/5 — 18/5 + 6*√59/5-10 = 68/5-68/5 = 0.
Таким образом, мы показали, что найденные корни уравнения являются истинными.
Видео:ФакториалСкачать
Метод №3. Применение известной формулы
Этот метод решения уравнений квадратных является, пожалуй, самым простым, поскольку он заключается в подставлении коэффициентов в известную формулу. Для его использования не нужно задумываться о составлении алгоритмов решения, достаточно запомнить только одну формулу. Она приведена на рисунке выше.
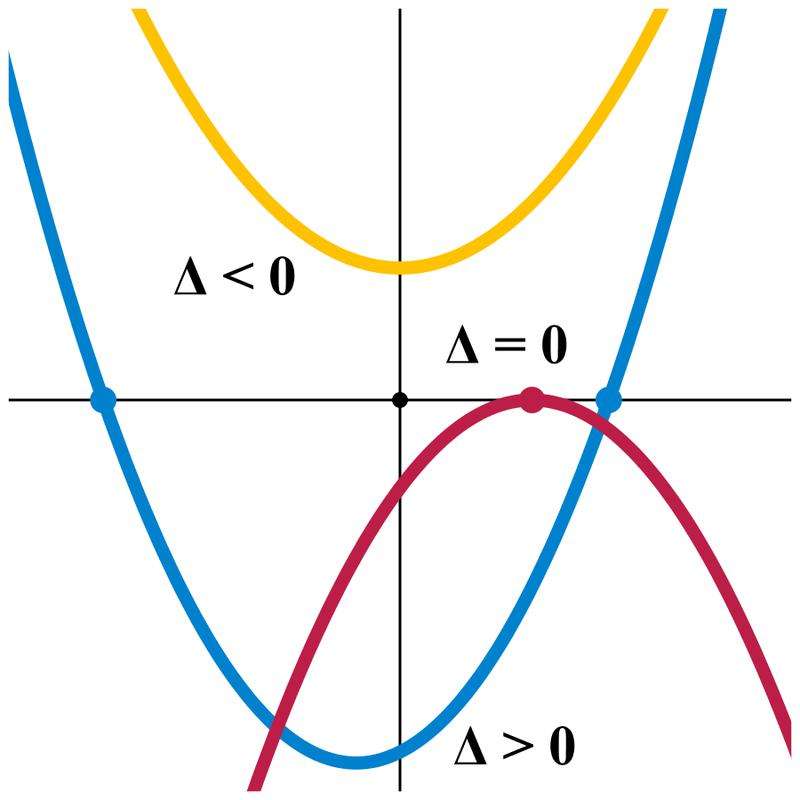
В этой формуле подкоренное выражение (b2-4*a*c) называется дискриминантом (D). От его значения зависит то, какие корни получатся. Возможны 3-и случая:
- D>0, тогда уравнение корня два имеет действительных и разных.
- D=0, тогда получается корень один, который можно вычислить из выражения x = -b/(a*2).
- D 0 — параболы ветви направлены вверх, наоборот, если a 0. Ее экстремум имеет координаты: x=4/10=2/5, y=-4*2/5+5*(2/5)2+10 = 9,2. Поскольку минимум кривой лежит над осью абсцисс (y=9,2), то она не пересекает последнюю ни при каких значениях x. То есть действительных корней приведенное уравнение не имеет.
Видео:Метод переброски при решении квадратных уравненийСкачать
Теорема Виета
Как выше было отмечено, эта теорема является следствием метода №3, который основан на применении формулы с дискриминантом. Суть теоремы Виета заключается в том, что она позволяет связать в равенство коэффициенты уравнения и его корни. Получим соответствующие равенства.
Воспользуемся формулой для вычисления корней через дискриминант. Сложим два корня, получаем: x1+x2 = -b/a. Теперь умножим корни друг на друга: x1*x2, после ряда упрощений получается число c/a.
Таким образом, для решения уравнений квадратных по теореме Виета можно использовать полученных два равенства. Если все три коэффициента уравнения известны, тогда корни можно найти путем решения соответствующей системы из этих двух уравнений.
Видео:Решение квадратных уравнений. Метод разложения на множители. 8 класс.Скачать
Пример использования теоремы Виета
Необходимо составить квадратное уравнение, если известно, что оно имеет вид x2+c = -b*x и корни его равны 3 и -4.
Поскольку в рассматриваемом уравнении a=1, то формулы Виета будут иметь вид: x2+x1 =-b и x2*x1= с. Подставляя известные значения корней, получаем: b = 1 и c = -12. В итоге восстановленное уравнение квадратное приведенное будет вид иметь: x2-12 = -1*x. Можно подставить в него значение корней и убедиться, что равенство выполняется.
Обратное применение Виета теоремы, то есть вычисление корней по известному виду уравнения, позволяет для небольших целых чисел a, b и c быстро (интуитивно) находить решения.
🎥 Видео
Решение квадратных уравненийСкачать
Комплексные корни квадратных уравнений. 11 класс.Скачать
Алгебра 8 класс (Урок№29 - Решение задач с помощью квадратных уравнений.)Скачать
Как решать квадратные уравнения без дискриминантаСкачать
Ещё один способ решения квадратных уравненийСкачать
