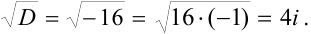Про уравнения - легко » Статьи

Решение квадратных уравнений с действительными коэффициентами и отрицательным дискриминантом

Обновлено
Решение квадратных уравнений с действительными коэффициентами и отрицательным дискриминантом

КОМПЛЕКСНЫЕ ЧИСЛА XI

§ 253. Извлечение корней квадратных из отрицательных чисел.
Решение квадратных уравнений с отрицательными дискриминантами

Таким образом, существуют по крайней мере два значения корня квадратного из — 1, а именно i и — i . Но, может быть, есть еще какие-нибудь комплексные числа, квадраты которых равны — 1?

Чтобы выяснить этот вопрос, предположим, что квадрат комплексного числа а + bi равен — 1. Тогда

Два комплексных числа равны тогда и только тогда, когда равны их действительные части и коэффициенты при мнимых частях. Поэтому

Согласно второму уравнению системы (1) хотя бы одно из чисел а и b должно равняться нулю. Если b = 0, то из первого уравнения получается а 2 = — 1. Число а действительное, и поэтому а 2 > 0. Неотрицательное число а 2 не может равняться отрицательному числу — 1. Поэтому равенство b = 0 в данном случае невозможно. Остается признать, что а = 0, но тогда из первого уравнения системы получаем: — b 2 = — 1, b = ± 1.

Следовательно, комплексными числами, квадраты которых равны —1, являются только числа i и —i, Условно это записывается в виде:

Аналогичными рассуждениями учащиеся могут убедиться в том, что существует ровно два числа, квадраты которых равны отрицательному числу —а. Такими числами являются √ a i и —√ a i . Условно это записывается так:

Под √ a здесь подразумевается арифметический, то есть положительный, корень. Например, √ 4 = 2, √ 9 =.3; поэтому

Если раньше при рассмотрении квадратных уравнений с отрицательными дискриминантами мы говорили, что такие уравнения не имеют корней, то теперь так говорить уже нельзя. Квадратные уравнения с отрицательными дискриминантами имеют комплексные корни. Эти корни получаются по известным нам формулам. Пусть, например, дано уравнение x 2 + 2х + 5 = 0; тогда

Итак, данное уравнение имеет два корня: х1 = — 1 +2i, х2 = — 1 — 2i. Эти корни являются взаимно сопряженными. Интересно отметить, что сумма их равна — 2, а произведение 5, так что выполняется теорема Виета.

2022. (У с т н о.) Решить уравнения:

2023. Найти все комплексные числа, квадраты которых равны:

2024. Решить квадратные уравнения:

Решить системы уравнений (№ 2025, 2026):

2027. Доказать, что корни квадратного уравнения с действительными коэффициентами и отрицательным дискриминантом являются взаимно сопряженными.

2028. Доказать, что теорема Виета верна для любых квадратных уравнений, а не только для уравнений с неотрицательным дискриминантом.

2029. Составить квадратное уравнение с действительными коэффициентами, корнями которого являются:

2030. Составить квадратное уравнение с действительными коэффициентами, один из корней которого равен (3 — i) (2i — 4).

2031. Составить квадратное уравнение с действительными коэффициентами, один из корней которого равен 32 — i
1— 3i .

Содержание
  1. Дискриминант
  2. Дискриминантом квадратного трехчлена называют выражение (b^-4ac), где (a, b) и (c) – коэффициенты данного трехчлена.
  3. Дискриминант и корни квадратного уравнения
  4. Значение дискриминанта показывает количество корней квадратного уравнения: — если (D) положителен – уравнение будет иметь два корня; — если (D) равен нулю – только один корень; — если (D) отрицателен – корней нет.
  5. Если дискриминант положителен
  6. Если дискриминант равен нулю
  7. Если дискриминант отрицателен
  8. Решение квадратных уравнений с отрицательным дискриминантом
  9. Пример №42.4.
  10. 🔍 Видео

Видео:Комплексные корни квадратного уравненияСкачать

Комплексные корни квадратного уравнения

Дискриминант

Дискриминантом квадратного трехчлена называют выражение (b^-4ac), где (a, b) и (c) – коэффициенты данного трехчлена.

Например, для трехчлена (3x^2+2x-7), дискриминант будет равен (2^2-4cdot3cdot(-7)=4+84=88). А для трехчлена (x^2-5x+11), он будет равен ((-5)^2-4cdot1cdot11=25-44=-19).

Дискриминант обозначается буквой (D) и часто используется при решении квадратных уравнений . Также по значению дискриминанта можно понять, как примерно выглядит график квадратичной функции (см. ниже).

Видео:Решение квадратных уравнений. Дискриминант. 8 класс.Скачать

Решение квадратных уравнений. Дискриминант. 8 класс.

Дискриминант и корни квадратного уравнения

Значение дискриминанта показывает количество корней квадратного уравнения:
— если (D) положителен – уравнение будет иметь два корня;
— если (D) равен нулю – только один корень;
— если (D) отрицателен – корней нет.

Это не надо учить, к такому выводу несложно прийти, просто зная, что квадратный корень из дискриминанта (то есть, (sqrt) входит в формулу для вычисления корней квадратного уравнения: (x_=) (frac<-b+sqrt>) и (x_=) (frac<-b-sqrt>) . Давайте рассмотрим каждый случай подробнее.

Видео:Отрицательный дискриминантСкачать

Отрицательный дискриминант

Если дискриминант положителен

В этом случае корень из него – это некоторое положительное число, а значит (x_) и (x_) будут различны по значению, ведь в первой формуле (sqrt) прибавляется, а во второй – вычитается. И мы имеем два разных корня.

Пример: Найдите корни уравнения (x^2+2x-3=0)
Решение:

Вычисляем дискриминант по формуле (D=b^2-4ac)

Найдем корни уравнения

Получили два различных корня из-за разных знаков перед (sqrt)

На графике квадратичной функции положительный дискриминант будет означать пересечение функции с осью икс ровно в двух точках – корнях уравнения. И это логично. Вдумайтесь – если уравнение (x^2+2x-3=0) имеет корни (x_=1) и (x_=-3), значит при подстановке (1) и (-3) вместо икса, левая часть станет нулем. А значит, если те же самые единицу и минус тройку подставить в функцию (y=x^2+2x-3) получим (y=0). То есть, функция (y=x^2+2x-3) проходит через точки ((1;0)) и ((-3;0)) (подробнее смотри статью Как построить график функции ).

Решение квадратных уравнений с действительными коэффициентами и отрицательным дискриминантом

Видео:Неполные квадратные уравнения. Алгебра, 8 классСкачать

Неполные квадратные уравнения. Алгебра, 8 класс

Если дискриминант равен нулю

А сколько корней будет, если дискриминант равен нулю? Давайте рассуждать.

Формулы корней выглядят так: (x_=) (frac<-b+sqrt>) и (x_=) (frac<-b-sqrt>) . И если дискриминант – ноль, то и корень из него тоже ноль. Тогда получается:

То есть, значения корней уравнения будут совпадать, потому что прибавление или вычитание нуля ничего не меняет.

Пример: Найдите корни уравнения (x^2-4x+4=0)
Решение:

Вычисляем дискриминант по формуле (D=b^2-4ac)

Находим корни уравнения

Получили два одинаковых корня, поэтому нет смысла писать их по отдельности – записываем как один.

На графике квадратичной функции нулевой дискриминант означает одну точку пересечения функции с осью икс. Все аналогично изложенному выше: два корня – две точки пересечения, один корень – одна. В частности, функция (y=x^2-4x+4) будет выглядеть вот так:

Решение квадратных уравнений с действительными коэффициентами и отрицательным дискриминантом

Видео:5 способов решения квадратного уравнения ➜ Как решать квадратные уравнения?Скачать

5 способов решения квадратного уравнения ➜ Как решать квадратные уравнения?

Если дискриминант отрицателен

В этом случае корень из дискриминанта извлечь нельзя (т.к. квадратный корень из отрицательного числа – невычислим), а значит и корни квадратного уравнения мы вычислить не можем.

Пример: Найдите корни уравнения (x^2+x+3=0)
Решение

Вычисляем дискриминант по формуле (D=b^2-4ac)

Находим корни уравнения

Оба корня содержат невычислимое выражение (sqrt), значит, и сами не вычислимы

То есть, отсутствие корней у квадратного уравнения с отрицательным дискриминантом – не чья-то случайная придумка. Это не потому что «в учебнике так написано», а действительно правда: невозможно найти такое число, чтоб при подстановке его вместо икса в выражение (x^2+x+3) получился ноль.

Матхак: заметим, что если вы решаете обычное квадратное уравнение или неравенство и получаете отрицательный дискриминант, стоит проверить решение еще раз, так как это не частая ситуация в школьном курсе математики.

Ну, а на графиках все просто: нет корней – нет точек пересечения с осью икс!

Видео:РАЗБИРАЕМ ДИСКРИМИНАНТ ЧАСТЬ I #shorts #математика #егэ #огэ #дискриминантСкачать

РАЗБИРАЕМ ДИСКРИМИНАНТ ЧАСТЬ I #shorts #математика #егэ #огэ #дискриминант

Решение квадратных уравнений с отрицательным дискриминантом

Рассмотрим решение квадратных уравнений, дискриминант которых отрицателен:

Решение квадратных уравнений с действительными коэффициентами и отрицательным дискриминантом

Пример №42.4.

Решить уравнение: 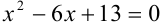Решение квадратных уравнений с действительными коэффициентами и отрицательным дискриминантом.

Решение:

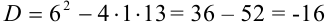
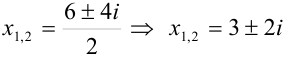
Найдем дискриминант: Решение квадратных уравнений с действительными коэффициентами и отрицательным дискриминантом.

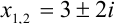
Решение квадратных уравнений с действительными коэффициентами и отрицательным дискриминантом

Тогда Решение квадратных уравнений с действительными коэффициентами и отрицательным дискриминантом.

Ответ: Решение квадратных уравнений с действительными коэффициентами и отрицательным дискриминантом.

Видим, что если дискриминант квадратного уравнения отрицателен, то уравнение имеет решения на множестве комплексных чисел. В ответе получаются два сопряженных комплексных числа. Это очень важный результат: теперь мы знаем, что абсолютно любое квадратное уравнение имеет два корня на множестве комплексных чисел.

Подобное утверждение, известное под названием «основная теорема алгебры», было доказано Гауссом в конце XVIII века: любое алгебраическое уравнение Решение квадратных уравнений с действительными коэффициентами и отрицательным дискриминантом-й степени имеет Решение квадратных уравнений с действительными коэффициентами и отрицательным дискриминантомкомплексных корней (при этом некоторые корни являются кратными). Эти результаты подчеркивают ту исключительную роль, которую играют комплексные числа в теории алгебраических уравнений.

Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:

Другие лекции по высшей математике, возможно вам пригодятся:

Решение квадратных уравнений с действительными коэффициентами и отрицательным дискриминантом

Решение квадратных уравнений с действительными коэффициентами и отрицательным дискриминантом Решение квадратных уравнений с действительными коэффициентами и отрицательным дискриминантом Решение квадратных уравнений с действительными коэффициентами и отрицательным дискриминантом Решение квадратных уравнений с действительными коэффициентами и отрицательным дискриминантом Решение квадратных уравнений с действительными коэффициентами и отрицательным дискриминантом Решение квадратных уравнений с действительными коэффициентами и отрицательным дискриминантом Решение квадратных уравнений с действительными коэффициентами и отрицательным дискриминантом Решение квадратных уравнений с действительными коэффициентами и отрицательным дискриминантом Решение квадратных уравнений с действительными коэффициентами и отрицательным дискриминантом Решение квадратных уравнений с действительными коэффициентами и отрицательным дискриминантом Решение квадратных уравнений с действительными коэффициентами и отрицательным дискриминантом Решение квадратных уравнений с действительными коэффициентами и отрицательным дискриминантом Решение квадратных уравнений с действительными коэффициентами и отрицательным дискриминантом Решение квадратных уравнений с действительными коэффициентами и отрицательным дискриминантом Решение квадратных уравнений с действительными коэффициентами и отрицательным дискриминантом Решение квадратных уравнений с действительными коэффициентами и отрицательным дискриминантом Решение квадратных уравнений с действительными коэффициентами и отрицательным дискриминантом Решение квадратных уравнений с действительными коэффициентами и отрицательным дискриминантом Решение квадратных уравнений с действительными коэффициентами и отрицательным дискриминантом Решение квадратных уравнений с действительными коэффициентами и отрицательным дискриминантом Решение квадратных уравнений с действительными коэффициентами и отрицательным дискриминантом Решение квадратных уравнений с действительными коэффициентами и отрицательным дискриминантом Решение квадратных уравнений с действительными коэффициентами и отрицательным дискриминантом Решение квадратных уравнений с действительными коэффициентами и отрицательным дискриминантом Решение квадратных уравнений с действительными коэффициентами и отрицательным дискриминантом Решение квадратных уравнений с действительными коэффициентами и отрицательным дискриминантом Решение квадратных уравнений с действительными коэффициентами и отрицательным дискриминантом Решение квадратных уравнений с действительными коэффициентами и отрицательным дискриминантом Решение квадратных уравнений с действительными коэффициентами и отрицательным дискриминантом Решение квадратных уравнений с действительными коэффициентами и отрицательным дискриминантом Решение квадратных уравнений с действительными коэффициентами и отрицательным дискриминантом Решение квадратных уравнений с действительными коэффициентами и отрицательным дискриминантом Решение квадратных уравнений с действительными коэффициентами и отрицательным дискриминантом Решение квадратных уравнений с действительными коэффициентами и отрицательным дискриминантом Решение квадратных уравнений с действительными коэффициентами и отрицательным дискриминантом Решение квадратных уравнений с действительными коэффициентами и отрицательным дискриминантом Решение квадратных уравнений с действительными коэффициентами и отрицательным дискриминантом Решение квадратных уравнений с действительными коэффициентами и отрицательным дискриминантом Решение квадратных уравнений с действительными коэффициентами и отрицательным дискриминантом Решение квадратных уравнений с действительными коэффициентами и отрицательным дискриминантом Решение квадратных уравнений с действительными коэффициентами и отрицательным дискриминантом Решение квадратных уравнений с действительными коэффициентами и отрицательным дискриминантом Решение квадратных уравнений с действительными коэффициентами и отрицательным дискриминантом Решение квадратных уравнений с действительными коэффициентами и отрицательным дискриминантом Решение квадратных уравнений с действительными коэффициентами и отрицательным дискриминантом Решение квадратных уравнений с действительными коэффициентами и отрицательным дискриминантом Решение квадратных уравнений с действительными коэффициентами и отрицательным дискриминантом Решение квадратных уравнений с действительными коэффициентами и отрицательным дискриминантом Решение квадратных уравнений с действительными коэффициентами и отрицательным дискриминантом Решение квадратных уравнений с действительными коэффициентами и отрицательным дискриминантом Решение квадратных уравнений с действительными коэффициентами и отрицательным дискриминантом Решение квадратных уравнений с действительными коэффициентами и отрицательным дискриминантом Решение квадратных уравнений с действительными коэффициентами и отрицательным дискриминантом

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

🔍 Видео

Комплексные корни квадратных уравнений. 11 класс.Скачать

Комплексные корни квадратных уравнений. 11 класс.

ОТРИЦАТЕЛЬНЫЙ ДИСКРИМИНАНТ 😉 #егэ #математика #профильныйегэ #shorts #огэСкачать

ОТРИЦАТЕЛЬНЫЙ ДИСКРИМИНАНТ 😉 #егэ #математика #профильныйегэ #shorts #огэ

Решение квадратных уравнений. Дискриминант. Практическая часть. 1ч. 8 класс.Скачать

Решение квадратных уравнений. Дискриминант. Практическая часть. 1ч. 8 класс.

Как решить квадратное уравнение за 30 секунд#математика #алгебра #уравнение #дискриминант #репетиторСкачать

Как решить квадратное уравнение за 30 секунд#математика #алгебра #уравнение #дискриминант #репетитор

Формула корней квадратного уравнения. Алгебра, 8 классСкачать

Формула корней квадратного уравнения. Алгебра, 8 класс

Квадратное уравнение. Как решить? | Математика ОГЭ 2023 | УмскулСкачать

Квадратное уравнение. Как решить? | Математика ОГЭ 2023 | Умскул

Решение квадратного уравнения с отрицательным дискриминантом. ПримерСкачать

Решение квадратного уравнения с отрицательным дискриминантом. Пример

КВАДРАТНОЕ УРАВНЕНИЕ дискриминантСкачать

КВАДРАТНОЕ УРАВНЕНИЕ дискриминант

Дробно-рациональные уравнения. 8 класс.Скачать

Дробно-рациональные уравнения. 8 класс.

Быстрый способ решения квадратного уравненияСкачать

Быстрый способ решения квадратного уравнения

Квадратные уравнения от «А» до «Я». Классификация, решение и теорема Виета | МатематикаСкачать

Квадратные уравнения от «А» до «Я». Классификация, решение и теорема Виета | Математика

4.Квадратное уравнение. Дискриминант отрицательный.Скачать

4.Квадратное уравнение. Дискриминант отрицательный.

Решение квадратных уравнений. Дискриминант. Практическая часть. 3ч. 8 класс.Скачать

Решение квадратных уравнений. Дискриминант. Практическая часть. 3ч. 8 класс.

Решение квадратных уравнений. Дискриминант. Практическая часть. 4ч. 8 класс.Скачать

Решение квадратных уравнений. Дискриминант. Практическая часть. 4ч. 8 класс.
Поделиться или сохранить к себе: