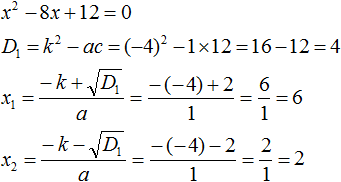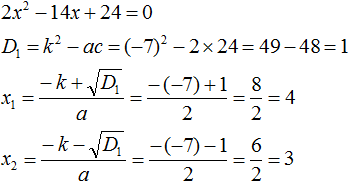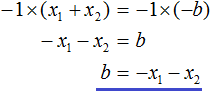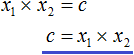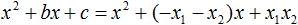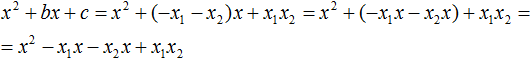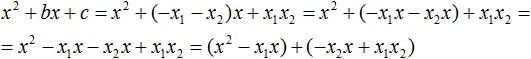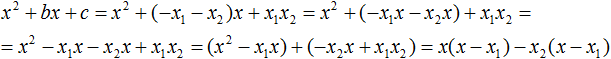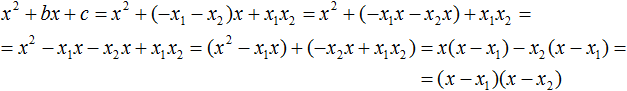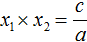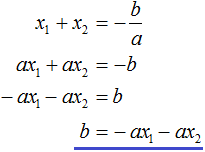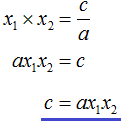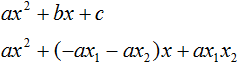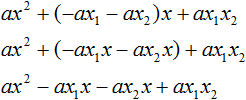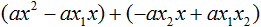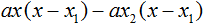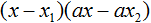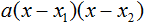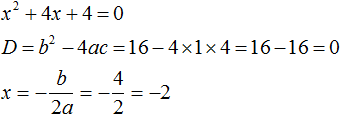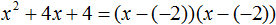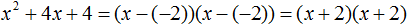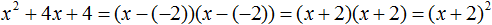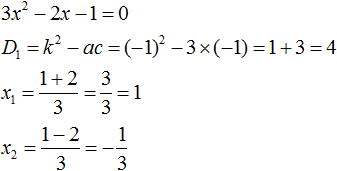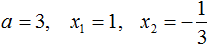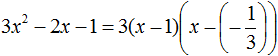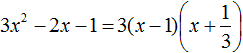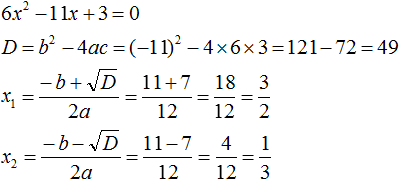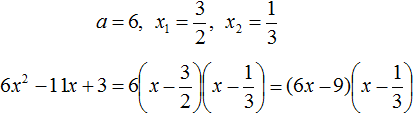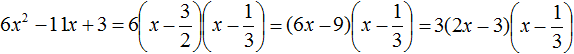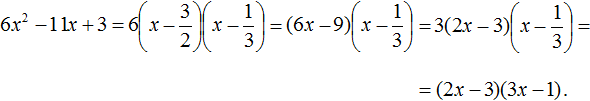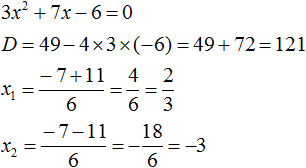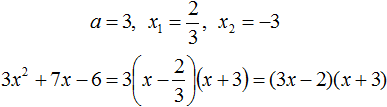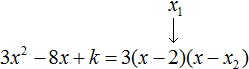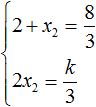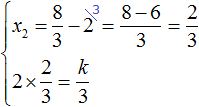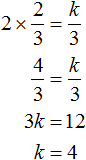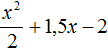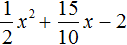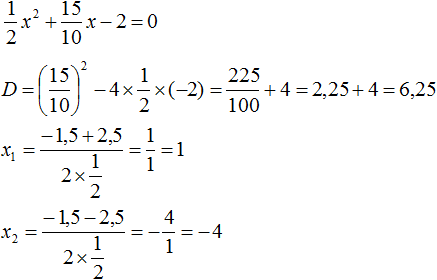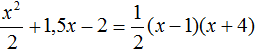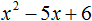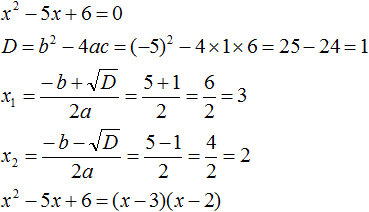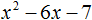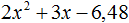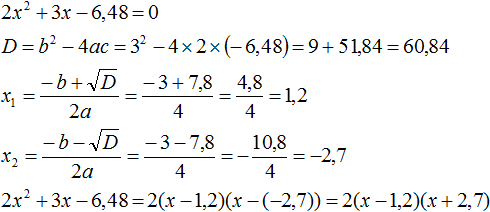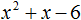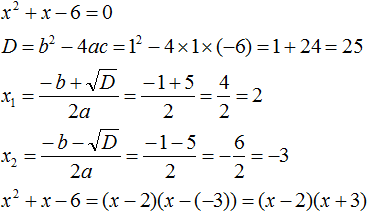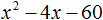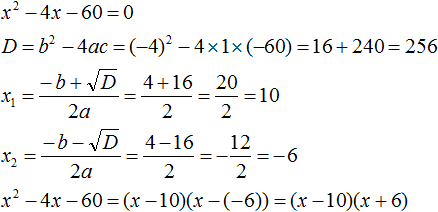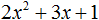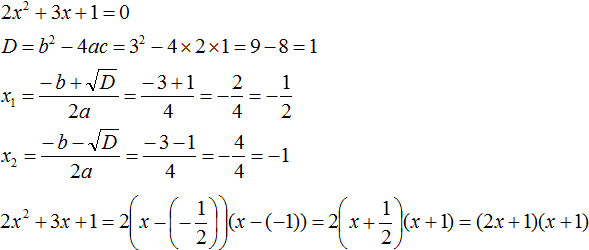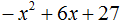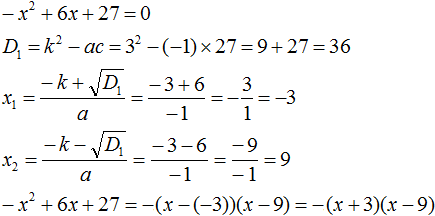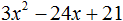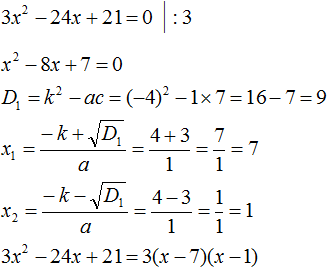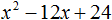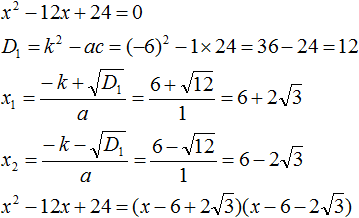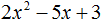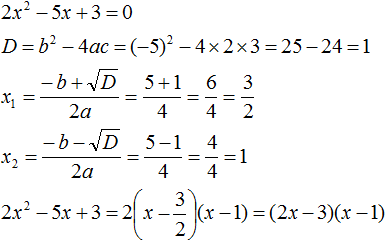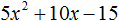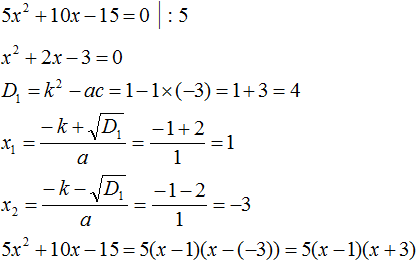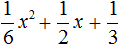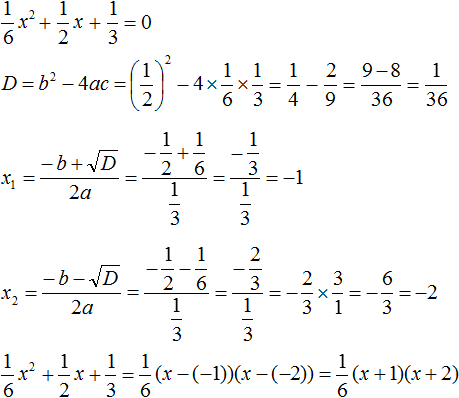Решение квадратных уравнений путем разложения на множители (3 видео)

Разложение квадратного трёхчлена на множители

Содержание

Как разложить на множители квадратный трёхчлен
Как это работает
Примеры разложений
Задания для самостоятельного решения
Разложение квадратного трёхчлена на множители
Решение квадратных уравнений путем разложения на множители
🔍 Видео

Видео:Решение квадратных уравнений. Метод разложения на множители. 8 класс.Скачать

Как разложить на множители квадратный трёхчлен

Квадратный трёхчлен — это многочлен вида ax 2 + bx + c .

В прошлых уроках мы решали квадратные уравнения. Общий вид таких уравнений выглядел так:

Левая часть этого уравнения является квадратным трёхчленом.

Одним из полезных преобразований при решении задач является разложение квадратного трёхчлена на множители. Для этого исходный квадратный трёхчлен приравнивают к нулю и решают квадратное уравнение. В этом случае говорят, что выполняется поиск корней квадратного трёхчлена.

Полученные корни x₁ и x₂ следует подстáвить в следующее выражение, которое и станет разложением:

Таким образом, чтобы разложить квадратный трёхчлен на множители при помощи решения квадратного уравнения, нужно воспользоваться следующей готовой формулой:

Где левая часть — исходный квадратный трёхчлен.

Пример 1. Разложить на множители следующий квадратный трёхчлен:

Найдём корни квадратного трёхчлена. Для этого приравняем данный квадратный трёхчлен к нулю и решим квадратное уравнение:

В данном случае коэффициент b является чётным. Поэтому можно воспользоваться формулами для чётного второго коэффициента. Чтобы сэкономить время, некоторые подробные вычисления можно пропустить:

Итак, x₁ = 6 , x₂ = 2 . Теперь воспользуемся формулой ax 2 + bx + c = a(x − x₁)(x − x₂). В левой части вместо выражения ax 2 + bx + c напишем свой квадратный трёхчлен x 2 − 8x + 12. А в правой части подставим имеющиеся у нас значения. В данном случае a = 1, x₁ = 6, x₂ = 2

Если a равно единице (как в данном примере), то решение можно записать покороче:

Чтобы проверить правильно ли разложен квадратный трёхчлен на множители, нужно раскрыть скобки у правой части получившегося равенства.

Раскроем скобки у правой части равенства, то есть в выражении (x − 6)(x − 2) . Если мы всё сделали правильно, то должен получиться квадратный трёхчлен x 2 − 8x + 12

Пример 2. Разложить на множители следующий квадратный трёхчлен:

Приравняем данный квадратный трёхчлен к нулю и решим уравнение:

Как и в прошлом примере коэффициент b является чётным. Поэтому можно воспользоваться формулами для чётного второго коэффициента:

Итак, x₁ = 4 , x₂ = 3 . Приравняем квадратный трехчлен 2x 2 − 14x + 24 к выражению a(x − x₁)(x − x₂) , где вместо переменных a , x₁ и x₂ подстáвим соответствующие значения. В данном случае a = 2

Выполним проверку. Для этого раскроем скобки у правой части получившегося равенства. Если мы всё сделали правильно, то должен получиться квадратный трёхчлен 2x 2 − 14x + 24

Видео:5 способов решения квадратного уравнения ➜ Как решать квадратные уравнения?Скачать

Как это работает

Разложение квадратного трёхчлена на множители происходит, если вместо коэффициентов квадратного трёхчлена подстáвить теорему Виета и выполнить тождественные преобразования.

Для начала рассмотрим случай, когда коэффициент a квадратного трёхчлена равен единице:

Вспоминаем, что если квадратное уравнение является приведённым, то теорема Виета имеет вид:

Тогда приведённый квадратный трехчлен x 2 + bx + c можно разложить на множители следующим образом. Сначала выразим b из уравнения x₁ + x₂ = −b . Для этого можно умножить обе его части на −1

Переменную c из теоремы Виета выражать не нужно — она уже выражена. Достаточно поменять местами левую и правую часть:

Теперь подставим выраженные переменные b и c в квадратный трёхчлен x 2 + bx + c

Раскроем скобки там где это можно:

В получившемся выражении выполним разложение многочлена на множители способом группировки. В данном случае удобно сгруппировать первый член со вторым, а третий с четвёртым:

Из первых скобок вынесем общий множитель x , из вторых скобок — общий множитель −x₂

Далее замечаем, что выражение ( x − x₁ ) является общим множителем. Вынесем его за скобки:

Но это был случай, когда исходный квадратный трёхчлен является приведённым. В нём коэффициент a равен единице. И соответственно, в формуле разложения такого квадратного трехчлена коэффициент a можно опустить.

Теперь рассмотрим случай, когда коэффициент a квадратного трёхчлена не равен единице. Это как раз тот случай, когда в формуле разложения присутствует перед скобками коэффициент a

Вспоминаем, что если квадратное уравнение не является приведённым, то есть имеет вид ax 2 + bx + c = 0 , то теорема Виета принимает следующий вид:

Это потому что теорема Виета работает только для приведённых квадратных уравнений. А чтобы уравнение ax 2 + bx + c = 0 стало приведённым, нужно разделить обе его части на a

Далее чтобы квадратный трёхчлен вида ax 2 + bx + c разложить на множители, нужно вместо b и c подставить соответствующие выражения из теоремы Виета. Но в этот раз нам следует использовать равенства 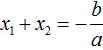и

Для начала выразим b и c . В первом равенстве умножим обе части на a . Затем обе части получившегося равенства умножим на −1

Теперь из второго равенства выразим c . Для этого умножим обе его части на a

Теперь подставим выраженные переменные b и с в квадратный трёхчлен ax 2 + bx + c . Для наглядности каждое преобразование будем выполнять на новой строчке:

Здесь вместо переменных b и c были подставлены выражения −ax₁ − ax₂ и ax₁x₂ , которые мы ранее выразили из теоремы Виета. Теперь раскроем скобки там где это можно:

Теперь из первых скобок вынесем общий множитель ax , а из вторых — общий множитель −ax₂

Далее замечаем, что выражение x − x₁ тоже является общим множителем. Вынесем его за скобки:

Вторые скобки содержат общий множитель a . Вынесем его за скобки. Его можно расположить в самом начале выражения:

Отметим, что если квадратный трехчлен не имеет корней, то его нельзя разложить на множители. Действительно, если не найдены корни квадратного трёхчлена, то нéчего будет подставлять в выражение a(x − x₁)(x − x₂) вместо переменных x₁ и x₂ .

Если квадратный трёхчлен имеет только один корень, то этот корень одновременно подставляется в x₁ и x₂ . Например, квадратный трёхчлен x 2 + 4x + 4 имеет только один корень −2

Тогда значение −2 в процессе разложения на множители будет подставлено вместо x₁ и x₂ . А значение a в данном случае равно единице. Её можно не записывать, поскольку это ничего не даст:

Скобки внутри скобок можно раскрыть. Тогда получим следующее:

При этом если нужно получить короткий ответ, последнее выражение можно записать в виде (x + 2) 2 поскольку выражение (x + 2)(x + 2) это перемножение двух сомножителей, каждый из которых равен (x + 2)

Видео:Математика| Разложение квадратного трехчлена на множители.Скачать

Примеры разложений

Пример 1. Разложить на множители следующий квадратный трёхчлен:

Найдём корни квадратного трёхчлена:

Воспользуемся формулой разложения. В левой части напишем квадратный трёхчлен 3x 2 − 2x − 1 , а в правой части — его разложение в виде a(x − x₁)(x − x₂) , где вместо a , x₁ и x₂ подстáвим соответствующие значения:

Во вторых скобках можно заменить вычитание сложением:

Пример 2. Разложить на множители следующий квадратный трёхчлен:

Упорядочим члены так, чтобы старший коэффициент располагался первым, средний — вторым, свободный член — третьим:

Найдём корни квадратного трёхчлена:

Воспользуемся формулой разложения:

Упростим получившееся разложение. Вынесем за первые скобки общий множитель 3

Теперь воспользуемся сочетательным законом умножения. Напомним, что он позволяет перемножать сомножители в любом порядке. Умножим 3 на вторые скобки. Это позвóлит избавиться от дроби в этих скобках:

Пример 3. Разложить на множители следующий квадратный трёхчлен:

Найдём корни квадратного трёхчлена:

Воспользуемся формулой разложения:

Пример 4. Найдите значение k , при котором разложение на множители трёхчлена 3x 2 − 8x + k содержит множитель (x − 2)

Если разложение содержит множитель (x − 2) , то один из корней квадратного трёхчлена равен 2 . Пусть корень 2 это значение переменной x₁

Чтобы найти значение k , нужно знать чему равен второй корень. Для его определения воспользуемся теоремой Виета.

В данном случае квадратный трёхчлен не является приведённым, поэтому сумма его корней будет равна дроби , а произведение корней — дроби

Выразим из первого равенства переменную x₂ и сразу подстáвим найденное значение во второе равенство вместо x₂

Теперь из второго равенства выразим k . Так мы найдём его значение.

Пример 5. Разложить на множители следующий квадратный трёхчлен:

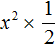
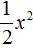
Перепишем данный трёхчлен в удобный для нас вид. Если в первом члене заменить деление умножением, то получим . Если поменять местами сомножители, то получится . То есть коэффициент a станет равным

Коэффициент b можно перевести в обыкновенную дробь. Так проще будет искать дискриминант:

Найдём корни квадратного трёхчлена:

Воспользуемся формулой разложения:

Видео:Разложение кубических выражений на множителиСкачать

Задания для самостоятельного решения

Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Возникло желание поддержать проект?
Используй кнопку ниже

Видео:Решение квадратных уравнений. Дискриминант. 8 класс.Скачать

Разложение квадратного трёхчлена на множители

Этот видеоурок доступен по абонементу

У вас уже есть абонемент? Войти

На данном уроке мы с вами научимся раскладывать квадратные трёхчлены на линейные множители. Для этого необходимо вспомнить теорему Виета и обратную ей. Данное умение поможет нам быстро и удобно раскладывать квадратные трёхчлены на линейные множители, а также упростит сокращение дробей, состоящих из выражений.

Если у вас возникнет сложность в понимании темы, рекомендуем посмотреть урок «Упрощение выражений»

Видео:Квадратный Трехчлен / Разложение квадратного трехчлена на множители, Как решать Квадратные УравненияСкачать

Решение квадратных уравнений путем разложения на множители

Определение 1. Квадратным уравнением называют уравнение вида

где коэффициенты а, b, с — любые действительные числа, причем а ≠ 0.

Коэффициенты а, b, с различают по названиям: а — первый, или старший, коэффициент; b — второй коэффициент, или коэффициент при х; с — свободный член.

Определение 2. Квадратное уравнение называют приведенным, если его старший коэффициент равен 1; квадратное уравнение называют неприведенным, если старший коэффициент отличен от 1.

— неприведенное квадратное уравнение (старший коэффициент равен 2), а уравнение

— приведенное квадратное уравнение.

Кроме приведенных и неприведенных квадратных уравнений различают также полные и неполные уравнения.

Определение 3. Полное квадратное уравнение — это квадратное уравнение, в котором присутствуют все три слагаемых; иными словами, это уравнение, у которого коэффициенты b и с отличны от нуля. Неполное квадратное уравнение — это уравнение, в котором присутствуют не все три слагаемых; иными словами, это уравнение, у которого хотя бы один из коэффициентов b, с равен нулю.

Обратите внимание: об ах 2 речи нет, этот член всегда присутствует в квадратном уравнении.

Опрелеление 4. Корнем квадратного уравнения

называют всякое значение переменной х, при котором квадратный трехчлен

обращается в нуль; такое значение переменной х называют также корнем квадратного трехчлена.

Можно сказать и так: корень квадратного уравнения

— это такое значение х, подстановка которого в уравнение обращает уравнение в верное числовое равенство 0 = 0.

Решить квадратное уравнение — значит найти все его корни или установить, что корней нет.

Сначала математики научились решать неполные квадратные уравнения, поскольку для этого не пришлось, как говорится, ничего изобретать. Рассмотрим несколько таких уравнений.

Пример 1. Решить неполные квадратные уравнения:

Поэтому либо х = 0, либо 2х — 7 = 0, откуда находим х = 3,5. Итак, уравнение имеет два корня: х₁ = 0, х₂ = 3,5.

Уравнение имеет два корня: х₁ = 0, х₂ = 5.

Ранее, мы уже говорили о том, что уравнение вида х 2 = а, где а > О, имеет два корня: и . Значит, для уравнения х 2 = 16 получаем х₁ = 4, x₂ = — 4 (мы учли, что ).

Допускается более экономная запись:

Уравнение имеет два корня: И в этом случае можно записать короче

Так как выражение Зx 2 неотрицательно при любых значениях х, то уравнение Зx 2 = — 10 не имеет корней. Иными словами, нет ни одного числа, подстановка которого вместо переменной х обратила бы это уравнение в верное числовое равенство.

Иногда в таких случаях уточняют: нет действительных корней. Дело в том, что в математике, кроме действительных чисел, рассматриваются так называемые мнимые числа; мнимые корни у этого уравнения есть.

е) Если 5x 2 = 0, то x 2 = 0, откуда x = 0 единственный корень уравнения.
Этот пример показывает, как решаются неполные квадратные уравнения:

1. Если уравнение имеет вид ах 2 = 0, то оно имеет один корень х = 0.

2. Если уравнение имеет вид , то используется метод разложения на множители: ; значит, либо x = 0, либо ах + b = 0. В итоге получаем два корня:

3. Если уравнение имеет вид , то его преобразуют к виду и далее . В случае, когда — отрицательное число, уравнение не имеет корней (значит, не имеет корней и исходное уравнение ). В случае, когда

— положительное число, т. е. , где m > 0, уравнение х 2 = m имеет два корня: (в этом случае, как мы условились выше, допускается более короткая запись:
).

Неполное квадратное уравнение, как мы только что видели, может иметь два корня, один корень, ни одного корня. То же можно сказать и о полном квадратном уравнении. Почему?

Мы с вами знаем, что графиком функции является парабола. Корнями квадратного уравнения служат абсциссы точек пересечения параболы с осью х. Парабола может пересекать ось х в двух точках, может касаться оси х, т. е. иметь с ней лишь одну общую точку, может вообще не пересекаться с осью х (рис. 92, а, б, в). Это значит, что квадратное уравнение может иметь либо два корня, либо один корень, либо вообще не иметь корней.

Конечно, неплохо знать, сколько корней имеет квадратное уравнение, но еще лучше уметь находить эти корни. Если уравнение неполное, то, как мы видели выше, особых проблем не возникает. А если мы имеем полное квадратное уравнение? Ниже на примере одного такого уравнения напомним, какими способами мы пользовались до сих пор, когда приходилось встречаться с квадратным уравнением.

Пример 2. Решить уравнение х 2 — 4х + 3 = 0.

I способ. Рассмотрим квадратный трехчлен х2 — 4х + 3 и разложим его на множители, используя способ группировки; предварительно представим слагаемое — 4х в виде — х — Зх. Имеем

Значит, заданное уравнение можно переписать в виде (х — 1) (х — 3) = 0, откуда ясно, что уравнение имеет два корня; х₁ = 1, х₂ = 3; при х = 1 обращается в нуль множитель х — 1, а при х = 3 обращается в нуль множитель х — 3.

II способ. Рассмотрим квадратный трехчлен х 2 — 4х + 3 и разложим его на множители, используя метод выделения полного квадрата; предварительно представим слагаемое 3 в виде 4-1. Имеем

Воспользовавшись формулой разности квадратов, получим

Рассуждая, как и в I способе, находим, что .

III способ. Построим график функции :

1) Имеем Значит, вершиной параболы является точка (2; -1), а осью параболы — прямая х = 2.

2) Возьмем на оси х две точки, симметричные относительно оси параболы, например точки х = 1 и х = 3. Имеем ; построим на координатной плоскости точки (1; 0) и (3; 0).

3) Через точки (1; 0), (2; -1), (3;0) проводим параболу (рис. 93).

Корнями уравнения х 2 — 4х + 3 = 0 служат абсциссы точек пересечения параболы с осью х. Таких точек две: (1; 0) и (3; 0). Итак, х₁ = 1, х₂ = 3.

IV способ. Преобразуем уравнение к виду х 2 — 4х — 3. Построим в одной системе координат графики функций у = х 2 и у = 4х — 3 (рис. 94). Они пересекаются в точках А( 1; 1) и B(3; 9). Корнями уравнения служат абсциссы точек А и B, поэтому х₁ = 1, х₂ = 3.

V способ. Преобразуем уравнение к виду x 2 + 3 = 4х. Построим в одной системе координат графики функций у = х 2 + 3 и у = 4х (рис. 95). Они пересекаются в точках А (1; 4) и B (3; 12). Корнями уравнения служат абсциссы точек А и B, таким образом,

VI способ. Преобразуем уравнение к виду и далее , т. е. . Построим в одной системе координат параболу у = (х — 2) 2 и прямую у = 1 (рис. 96). Они пересекаются в точках А (1; 1) и B(3; 1). Корнями уравнения служат абсциссы точек А и B, следовательно, .

VII способ. Разделив почленно обе части уравнения на х, получим

Построим в одной системе координат гиперболу прямую у = х — 4. Они пересекаются в точках А (1; -3) и (3; — 1) (рис. 97). Корнями уравнения служат абсциссы точек А и B, значит,

Итак, мы решили уравнение х 2 — 4х + 3 = 0 семью способами. Тем не менее знание этих способов не есть, как говорится, панацея от всех бед. Ведь наши успехи в решении квадратных уравнений зависели до сих пор от наличия одного из двух благоприятных обстоятельств:

1) квадратный трехчлен удавалось разложить на множители;

2) графики, которые мы использовали для графического решения уравнения, пересекались в «хороших» точках.

Надеяться на такие подарки судьбы математики, естественно, не могли. Они искали универсальный способ, пригодный для решения любых квадратных уравнений, и нашли его.