Видео:Решение квадратных уравнений. Дискриминант. 8 класс.Скачать
Формулировка теоремы Герона
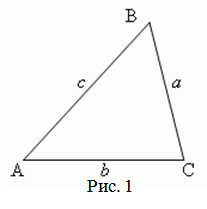
Площадь треугольника равна корню из произведения разностей полупериметра $p$ треугольника (рис 1) и каждой из его сторон $a$, $b$ и $c$ на полупериметр:
Треугольник со сторонами $a$, $b$ и $c$.
Формула Герона позволяет вычислить площадь треугольника по известным длинам его сторон.
Эта формула содержится в «Метрике» греческого математика и механика Герона Александрийского и названа в его честь. Герон интересовался треугольниками с целочисленными сторонами. Такие треугольники носят название героновых треугольников. Простейшим героновым треугольником является египетский треугольник — прямоугольный треугольник со соотношениями сторон $3 : 4 : 5$ .
Видео:Как решать квадратные уравнения без дискриминантаСкачать
Примеры решения задач
Задание. Вычислите площадь треугольника, зная, что его стороны равны 6 см; 5 см и 2,2 см.
Решение. Полупериметр
Тогда площадь треугольника, согласно формуле Герона, равна:
Ответ. $S=5.28left(mathrm^right)$
Видео:5 способов решения квадратного уравнения ➜ Как решать квадратные уравнения?Скачать
Формула Герона для треугольника
В данной публикации мы рассмотрим формулу Герона, пользуясь которой можно найти площадь треугольника. Также разберем примеры решения задач для того, чтобы закрепить представленный материал.
Видео:ТЕОРЕМА ВИЕТА ЗА 2 МИНУТЫСкачать
Формула площади
Площадь треугольника ( S ) равняется квадратному корню из произведения его полупериметра ( p ) на разности полупериметра и каждой из его сторон ( a, b, c ).
Полупериметр ( p ) вычисляется таким образом:
Примечание: для использования формулы необходимо знать/найти длину всех сторон треугольника.
Формула получила такое название в честь греческого математика и механика Герона Александрийского, который изучал треугольники с целочисленными сторонами и площадью (героновские). К таким, например, относится прямоугольный треугольник с соотношением сторон 3:4:5, который также называют египетским.
Видео:Быстрый способ решения квадратного уравненияСкачать
Примеры задач
Задание 1
Найдите площадь треугольника со сторонами 6, 8 и 10 см.
Решение
Для начала найдем полупериметр:
p = (6 + 8 + 10) / 2 = 12 см.
Теперь воспользуемся формулой Герона, подставив в нее заданные значения:
= .
Задание 2
В прямоугольном треугольнике длина гипотенузы равняется 15 см, а одного из катетов – 9 см. Вычислите площадь фигуры.
Решение
Пусть гипотенуза – это c , известный катет – a , а неизвестный – b .
Применим Теорему Пифагора, чтобы найти длину катета b :
b 2 = = = , следовательно,
Полупериметр треугольника равен:
p = (9 + 12 + 15) / 2 = 18 см.
Остается только использовать формулу для нахождения площади:
= = .
Видео:Формула корней квадратного уравнения. Алгебра, 8 классСкачать
Формула Герона
Вы будете перенаправлены на Автор24
Видео:Решение квадратных уравнений. Дискриминант. Практическая часть. 1ч. 8 класс.Скачать
Предварительные сведения
Для начала введем сведения и обозначения, которые будут необходимы нам в дальнейшем.
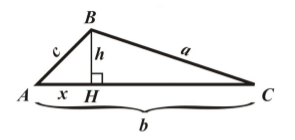
Будем рассматривать треугольник $ABC$ с острыми углами $A$ и $C$. Проведем в нем высоту $BH$. Введем следующие обозначения: $AB=c, BC=a, $$AC=b, AH=x, BH=h $(рис. 1).
Введем без доказательств теорему о площади треугольника.
Площадь треугольника определяется как половина произведения длины его стороны, на высоту, проведенную к ней, то есть
Видео:Квадратные уравнения от «А» до «Я». Классификация, решение и теорема Виета | МатематикаСкачать
Формула Герона
Введем и докажем теорему о нахождении площади треугольника по трем известным сторонам. Эта формула носит название формулы Герона.
Пусть нам даны три стороны треугольника $a, b и c$. Тогда площадь этого треугольника выражается следующим образом
где $p$ — полупериметр данного треугольника.
Доказательство.
Будем пользоваться обозначениями, введенными на рисунке 1.
Рассмотрим треугольник $ABH$. По теореме Пифагора, получим
Очевидно, что $HC=AC-AH=b-x$
Рассмотрим треугольник $ CBH$. По теореме Пифагора, получим
Приравняем значения квадрата высоты из двух полученных соотношений
Из первого равенства найдем высоту
Так как полупериметр равен $p=frac$, то есть $a+b+c=2p$, то
По теореме 1, получим
Теорема доказана.
Готовые работы на аналогичную тему
Видео:Решение квадратного уравнения с выводом формулы корнейСкачать
Примеры задач на использование формулы Герона
Найти площадь треугольника, если его стороны равняются $3$ см, $6$ см и $7$ см.
Решение.
Найдем вначале полупериметр этого треугольника
По теореме 2, получим
Ответ: $4sqrt$.
Найти площадь параллелепипеда, со сторонами $8$ см и $5$ см и меньшей диагональю, равной $5$ см.
Решение.
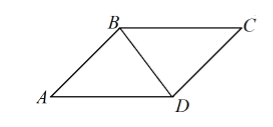
Пусть нам дан параллелограмм $ABCD$, где $AD=8 см, AB=5 см и BD=5 см$ (рис. 2).
Так как диагональ параллелограмма является его осью симметрии, то треугольники $ABD$ и $BDC$ равны между собой. Следовательно
Полупериметр треугольника $ABD$ равен
Ответ: $24$.
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата последнего обновления статьи: 20 05 2021
💥 Видео
Квадратное уравнение, дискриминант, формула корнейСкачать
Квадратные уравнения #shorts Как решать квадратные уравненияСкачать
Как решить квадратное уравнение (Положительный дискриминант)Скачать
МАТЕМАТИКА 8 класс - Квадратные Уравнения. Как решать Квадратные Уравнения? Формула КорнейСкачать
Как решать квадратные уравнения. 8 класс. Вебинар | МатематикаСкачать
КВАДРАТНОЕ УРАВНЕНИЕ дискриминантСкачать
Формула для корней и теорема Виета | Квадратный трёхчлен #1 | Ботай со мной #020 | Борис ТрушинСкачать
Решение квадратных уравнений. Метод разложения на множители. 8 класс.Скачать
Квадратные уравнения: 9 способов решения(Не только дискриминант)Скачать
Квадратное уравнение. 8 класс.Скачать
Комплексные корни квадратных уравнений. 11 класс.Скачать
