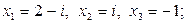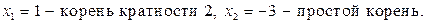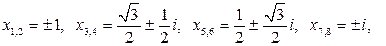1. Решите следующие квадратные уравнения относительно неизвестрной х на множестве комплексных чисел и сделайте проверку по теореме Виета:
1) 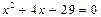
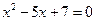
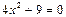
4) 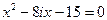
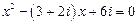
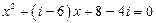
2. Решите следующие двучленные уравнения на множестве комплексных чисел:
1) 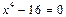
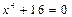
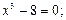
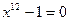
3. Найдите все корни следующих алгебраических уравнений на множестве комплексных чисел:
1) 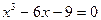
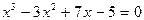
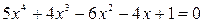
4) 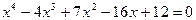
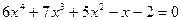
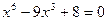
4.Составьте алгебраические уравнения наименьшей степени с действительными коэффициентами, корнями которого являются заданные числа:
1) 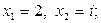
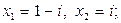
4)
Ответы к упражнениям для самостоятельной работы
1. 1) 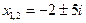
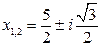
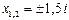
4) 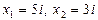
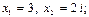
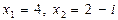
2. 1) 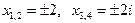
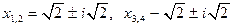
3) 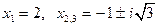
4)
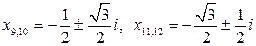
3. 1) 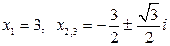
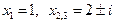
3) 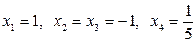
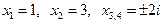
5) 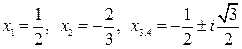
6) 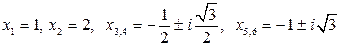
4. 1) 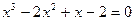
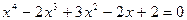
3) 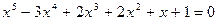
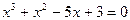
Вопросы для самопроверки
Что называется целой алгебраической функцией или алгебраическим многочленом (полиномом)?
Что такое степень многочлена?
Что такое коэффициенты многочлена?
Что называется алгебраическим уравнением n-й степени?
Что называется нулем функции?
Что называется корнем уравнения?
Сформулируйте свойство о тождественном равенстве алгебраических многочленов.
Сформулируйте свойство о делении целого многочлена на разность (x – х0)
Сформулируйте теорему о делении целого многочлена на двучлен без остатка
Сформулируйте свойство о существовании нуля многочлена, основная теорема алгебры
Сформулируйте свойство о разложении многочлена на линейные множители
Что называется k-кратным корнем многочлена Pn(x), или корнем кратности k?
Что называется простым корнем многочлена Pn(x)?
Сформулируйте свойство о количестве корней алгебраического уравнения
Сформулируйте свойство о комплексных корнях алгебраического уравнения
Сформулируйте свойство о разложении целого многочлена с действительными коэффициентами на линейные и квадратичные множители?
Сформулируйте свойство о целых и рациональных корнях алгебраического уравнения с действительными целыми коэффициентами
Что такое теорема Виета?
k-кратным корнем многочлена Pn(x), или корнем кратности k называется…(стр. 169)
алгебраическим уравнением n-й степени называется…(стр. 165)
корнем уравнения называется…(стр. 165)
коэффициенты многочлена это…(стр. 164)
нулем функции называется…(стр. 165)
простым корнем многочлена Pn(x) называется…(стр. 169)
степень многочлена это…(стр. 164)
теорема Виета это…(стр. 173)
целой алгебраической функцией или алгебраическим многочленом (полиномом) называется…(стр. 164)
Дата добавления: 2015-10-19 ; просмотров: 861 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Видео:Комплексные корни квадратного уравненияСкачать

Самостоятельная работа по теме «Комплексные числа» 11 класс алгебра
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Рабочие листы и материалы для учителей и воспитателей
Более 300 дидактических материалов для школьного и домашнего обучения
Самостоятельная работа «Комплексные числа»
a) 
b) 
c) 
d) 
e)
2. Представьте комплексное число в тригонометрической форме:
а) 
b)
Самостоятельная работа «Комплексные числа»
a) 
b) 
c) 
d) 
e)
2. Представьте комплексное число в тригонометрической форме:
а) 
b)
Самостоятельная работа «Комплексные числа»

a) 
b) 
c) 
d) 
e)
2. Представьте комплексное число в тригонометрической форме:
а) 
b)
Самостоятельная работа «Комплексные числа»
a) 
b) 
c) 
d) 
e)
2. Представьте комплексное число в тригонометрической форме:
а) 
b)
Самостоятельная работа «Комплексные числа»
a) 
b) 
c) 
d) 
e)
2. Представьте комплексное число в тригонометрической форме:
а) 
b)
Самостоятельная работа «Комплексные числа»

a) 
b) 
c) 
d) 
e)
2. Представьте комплексное число в тригонометрической форме:
а) 
b)
Видео:10 класс, 35 урок, Комплексные числа и квадратные уравненияСкачать

Квадратное уравнение с комплексными корнями и коэффициентами
Пусть задано квадратное уравнение $ax^2+bx+c=0$, где коэффициенты $a$, $b$ и $c$ — в общем случае являются комплексными. Его решение находим с помощью дискриминанта
В общем случае и дискриминант, и корни уравнения являются комплексными числами.
Задание. Составить квадратное уравнение, которое имеет корни $z_=1-i$ и $z_=4-5i$. Решить его.
Решение. Известно, что если $z_1$, $z_2$ — корни квадратного уравнения $z^2+bz+c=0$, то указанное уравнение можно записать в виде $(z-z_1)(z-z_2)=0$. А тогда, учитывая этот факт, имеем, что искомое уравнение можно записать следующим образом:
Раскрываем скобки и выполняем операции над комплексными числами:
$z^+(-5+6 i) z-(1+9 i)=0$ — искомое квадратное уравнение.
Решим полученное уравнение. Найдем дискриминант:
$$D=(-5+6 i)^-4 cdot 1 cdot(-(1+9 i))=-11-60 i+4+36 i=$$ $$=-7-24 i$$
Так как при извлечении корня из комплексного числа в результате получится комплексное число, то корень из дискриминанта будем искать в виде $sqrt=a+b i$. То есть
$$sqrt=a+b i Rightarrow-7-24 i=(a+b i)^ Rightarrow$$ $$Rightarrow-7-24 i=a^+2 a b i-b^$$
Используя тот факт, что два комплексных числа будут равными, если равны их действительные и мнимые части соответственно, получим систему для нахождения неизвестных значений $a$ и $b$:
решив которую, имеем, что $a_1=3$, $b_1=-4$ или $a_2=-3$, $b_2=4$. Рассматривая любую из полученных пар, например, первую, получаем, что $sqrt=3-4 i$, а тогда
Ответ. $z^+(-5+6 i) z-(1+9 i)=0$
📺 Видео
Комплексные корни квадратных уравнений. 11 класс.Скачать

Решение квадратных уравнений. Дискриминант. 8 класс.Скачать

КОМПЛЕКСНЫЕ ЧИСЛА ДЛЯ ЧАЙНИКОВ ЗА 7 МИНУТСкачать

5 способов решения квадратного уравнения ➜ Как решать квадратные уравнения?Скачать

Решение квадратных уравнений в поле комплексных чиселСкачать

Комплексные числа в уравненияхСкачать

Решение квадратных уравнений. Метод разложения на множители. 8 класс.Скачать

Квадратные уравнения от «А» до «Я». Классификация, решение и теорема Виета | МатематикаСкачать

Математика это не ИсламСкачать

Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать

Биквадратное уравнение. Комплексные корни.Скачать

Комплексные числа. Разбор задач. Задача 2.1Скачать

Математика| Разложение квадратного трехчлена на множители.Скачать

Как решать квадратные уравнения. 8 класс. Вебинар | МатематикаСкачать

@Квадратные уравнение в комплексных числах #математикаСкачать

Решение биквадратных уравнений. 8 класс.Скачать

Алгебра 8. Урок 9 - Квадратные уравнения. Полные и неполныеСкачать

Математика без Ху!ни. Комплексные числа, часть 1. Введение.Скачать