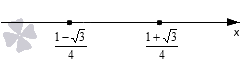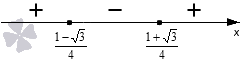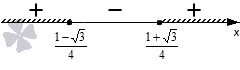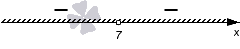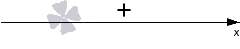Решение квадратных уравнений методом интервалов

Универсальным методом решения неравенств по праву считается метод интервалов. Именно его проще всего использовать для решения квадратных неравенств с одной переменной. В этом материале мы рассмотрим все аспекты применения метода интервалов для решения квадратных неравенств. Для облегчения усвоения материала мы рассмотрим большое количество примеров разной степени сложности.

Видео:Решение неравенства методом интерваловСкачать

Алгоритм применения метода интервалов

Рассмотрим алгоритм применения метода интервалов в адаптированном варианте, который пригоден для решения квадратных неравенств. Именно с таким вариантом метода интервалов знакомят учеников на уроках алгебры. Не будем усложнять задачу и мы.

Перейдем собственно к алгоритму.

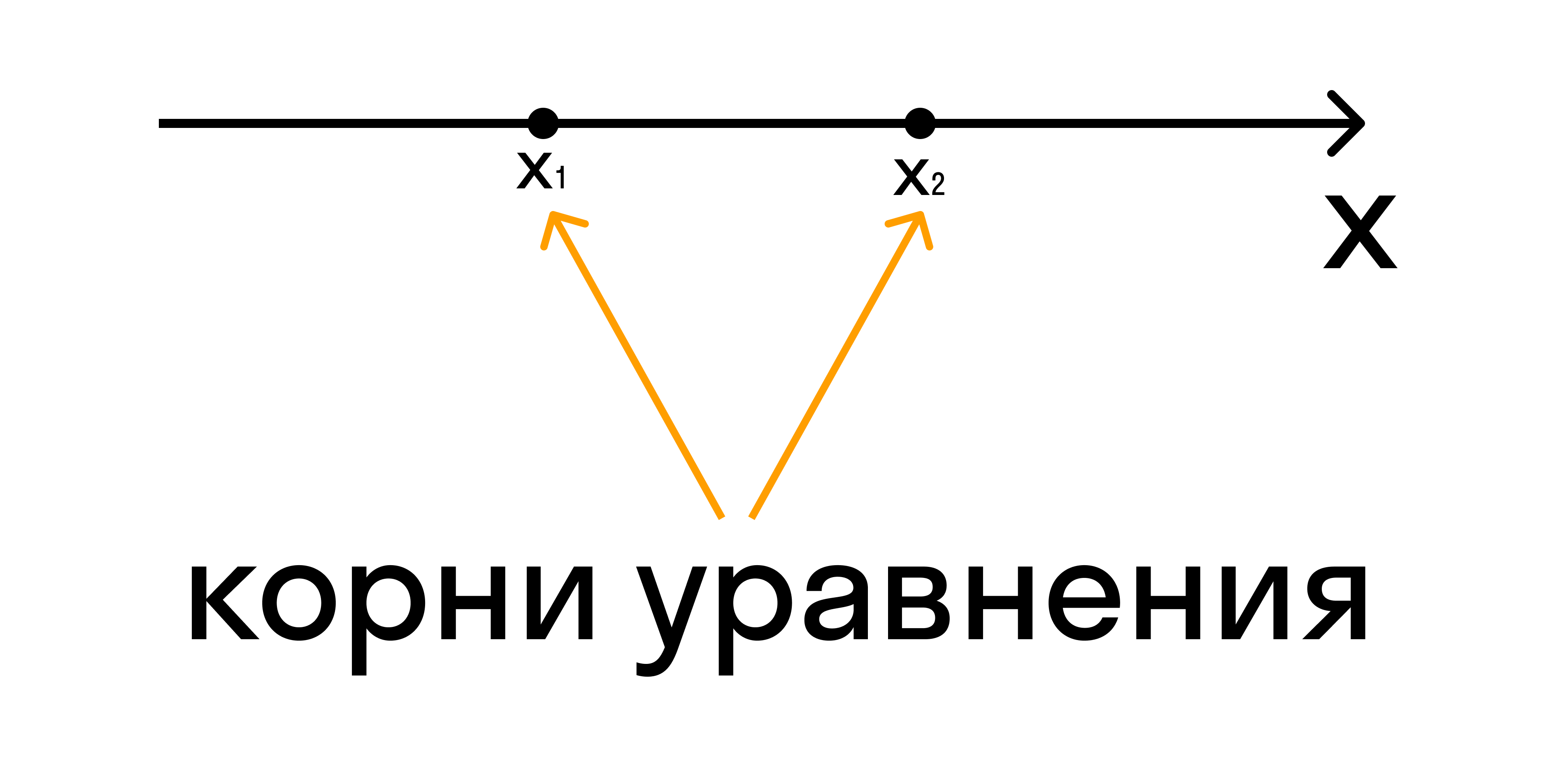
У нас есть квадратный трехчлен a · x 2 + b · x + c из левой части квадратного неравенства. Находим нули из этого трехчлена.

В системе координат изображаем координатную прямую. Отмечаем на ней корни. Для удобства можем ввести разные способы обозначения точек для строгих и нестрогих неравенств. Давайте договоримся, что «пустыми» точками мы будем отмечать координаты при решении строгого неравенства, а обычными точками — нестрогого. Отметив точки, мы получаем на координатной оси несколько промежутков.

Если на первом шаге мы нашли нули, то определяем знаки значений трехчлена для каждого из полученных промежутков. Если нули мы не получили, то производим это действие для всей числовой прямой. Отмечаем промежутки знаками « + » или « — ».

Дополнительно мы будем вводить штриховку в тех случаях, когда будем решать неравенства со знаками > или ≥ и или ≤ . В первом случае штриховка будет наноситься над промежутками, отмеченными « + », во втором над участками, отмеченными « — ».

Отметив знаки значений трехчлена и нанеся штриховку над отрезками, мы получаем геометрический образ некоторого числового множества, которое фактически является решением неравенства. Нам остается лишь записать ответ.

Остановимся подробнее на третьем шаге алгоритма, который предполагает определение знака промежутка. Существует несколько подходов определения знаков. Рассмотрим их по порядку, начав с наиболее точного, хотя и не самого быстрого. Этот метод предполагает вычисление значений трехчлена в нескольких точках полученных промежутков.

Для примера возьмем трехчлен x 2 + 4 · x − 5 .

Корни этого трехчлена 1 и — 5 разбивают координатную ось на три промежутка ( − ∞ , − 5 ) , ( − 5 , 1 ) и ( 1 , + ∞ ) .

Начнем с промежутка ( 1 , + ∞ ) . Для того, чтобы упростить себе задачу, примем х = 2 . Получаем 2 2 + 4 · 2 − 5 = 7 .

7 – положительное число. Это значит, что значения данного квадратного трехчлена на интервале ( 1 , + ∞ ) положительные и его можно обозначить знаком « + ».

Для определения знака промежутка ( − 5 , 1 ) примем x = 0 . Имеем 0 2 + 4 · 0 − 5 = − 5 . Ставим над интервалом знак « — ».

Для промежутка ( − ∞ , − 5 ) возьмем x = − 6 , получаем ( − 6 ) 2 + 4 · ( − 6 ) − 5 = 7 . Отмечаем этот интервал знаком « + ».

Намного быстрее определить знаки можно с учетом следующих фактов.

При положительном дискриминанте квадратный трехчлен с двумя корнями дает чередование знаков его значений на промежутках, на которые разбивается числовая ось корнями этого трехчлена. Это значит, что нам вовсе не обязательно определять знаки для каждого из интервалов. Достаточно провести вычисления для одного и проставить знаки для остальных, учитывая принцип чередования.

При желании, можно и вовсе обойтись без вычислений, сделав выводы о знаках по значению старшего коэффициента. Если a > 0 , то мы получаем последовательность знаков + , − , + , а если a 0 – то − , + , − .

У квадратных трехчленов с одним корнем, когда дискриминант равен нулю, мы получаем два промежутка на координатной оси с одинаковыми знаками. Это значит, что мы определяем знак для одного из промежутков и для второго ставим такой же.

Здесь также применим метод определения знака на основе значения коэффициента a : если a > 0 , то будет + , + , а если a 0 , то − , − .

Если квадратный трехчлен не имеет корней, то знаки его значений для всей координатной прямой совпадают как со знаком старшего коэффициента a , так и со знаком свободного члена c .

Например, если мы возьмем квадратный трехчлен − 4 · x 2 − 7 , он не имеет корней (его дискриминант отрицательный). Коэффициент при x 2 есть отрицательное число − 4 , и свободный член − 7 тоже отрицателен. Это значит, что на промежутке ( − ∞ , + ∞ ) его значения отрицательны.

Видео:Алгебра 9. Урок 7 - Неравенства. Метод интервалов - основные фактыСкачать

Примеры решения квадратных неравенств

Рассмотрим примеры решения квадратных неравенств с использованием рассмотренного выше алгоритма.

Решите неравенство 8 · x 2 − 4 · x − 1 ≥ 0 .

Решение

Используем для решения неравенства метод интервалов. Для этого найдем корни квадратного трехчлена 8 · x 2 − 4 · x − 1 . В связи с тем, что коэффициент при х четный, нам будет удобнее вычислить не дискриминант, а четвертую часть дискриминанта: D ‘ = ( − 2 ) 2 − 8 · ( − 1 ) = 12 .

Дискриминант больше нуля. Это позволяет нам найти два корня квадратного трехчлена: x 1 = 2 — 12 9 , x 1 = 1 — 3 4 и x 2 = 2 + 12 8 , x 2 = 1 + 3 4 . Отметим эти значения на числовой прямой. Так как уравнение нестрогое, то на графике мы используем обычные точки.

Теперь по методу интервалов определяем знаки трех полученных интервалов. Коэффициент при x 2 равен 8 , то есть, положителен, следовательно, последовательность знаков будет + , − , + .

Так как мы решаем неравенство со знаком ≥ , то изображаем штриховку над промежутками со знаками плюс:

Запишем аналитически числовое множество по полученному графическому изображению. Мы можем сделать это двумя способами:

( — ∞ ; 1 — 3 4 ] ∪ [ 1 + 3 4 , + ∞ ) или x ≤ 1 — 3 4 , x ≥ 1 + 3 4 .

Ответ: ( — ∞ ; 1 — 3 4 ] ∪ [ 1 + 3 4 , + ∞ ) или x ≤ 1 — 3 4 , x ≥ 1 + 3 4 .

Выполните решение квадратного неравенства — 1 7 · x 2 + 2 · x — 7 0 методом интервалов.

Решение

Для начала найдем корни квадратного трехчлена из левой части неравенства:

D ‘ = 1 2 — — 1 7 · — 7 = 0 x 0 = — 1 — 1 7 x 0 = 7

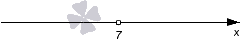
Это строгое неравенство, поэтому на графике используем «пустую» точку. С координатой 7 .

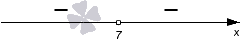
Теперь нам нужно определить знаки на полученных промежутках ( − ∞ , 7 ) и ( 7 , + ∞ ) . Так как дискриминант квадратного трехчлена равен нулю, а старший коэффициент отрицательный, то мы проставляем знаки − , − :

Так как мы решаем неравенство со знаком , то изображаем штриховку над интервалами со знаками минус:

В данном случае решениями являются оба промежутка ( − ∞ , 7 ) , ( 7 , + ∞ ) .

Ответ: ( − ∞ , 7 ) ∪ ( 7 , + ∞ ) или в другой записи x ≠ 7 .

Имеет ли квадратное неравенство x 2 + x + 7 0 решения?

Решение

Найдем корни квадратного трехчлена из левой части неравенства. Для этого найдем дискриминант: D = 1 2 − 4 · 1 · 7 = 1 − 28 = − 27 . Дискриминант меньше нуля, значит, действительных корней нет.

Графическое изображение будет иметь вид числовой прямой без отмеченных на ней точек.

Определим знак значений квадратного трехчлена. При D 0 он совпадает со знаком коэффициента при x 2 , то есть, со знаком числа 1 , оно положительное, следовательно, имеем знак + :

Штриховку мы могли бы нанести в данном случае над промежутками со знаком « — ». Но таких промежутков у нас нет. Следовательно, чертеж сохраняет вот такой вид:

В результате вычислений мы получили пустое множество. Это значит, что данное квадратное неравенство решений не имеет.

Видео:Решение квадратных неравенств методом интервалов. 8 класс.Скачать

Метод интервалов, решение неравенств

О чем эта статья:

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Видео:Решение квадратных неравенств | МатематикаСкачать

Определение квадратного неравенства

Неравенство — алгебраическое выражение, в котором используются знаки ≠, , ≤, ≥.

Числовое неравенство — это такое неравенство, в записи которого по обе стороны от знака находятся числа или числовые выражения.

Решение — значение переменной, при котором неравенство становится верным.

Решить неравенство значит найти множество, для которых оно выполняется.

Квадратное неравенство выглядит так:

где x — переменная,

Квадратное неравенство можно решить двумя способами:

• графический метод;
• метод интервалов.

Видео:Как понять неравенства? Квадратные неравенства. Линейные и сложные неравенства | TutorOnlineСкачать

Решение неравенства графическим методом

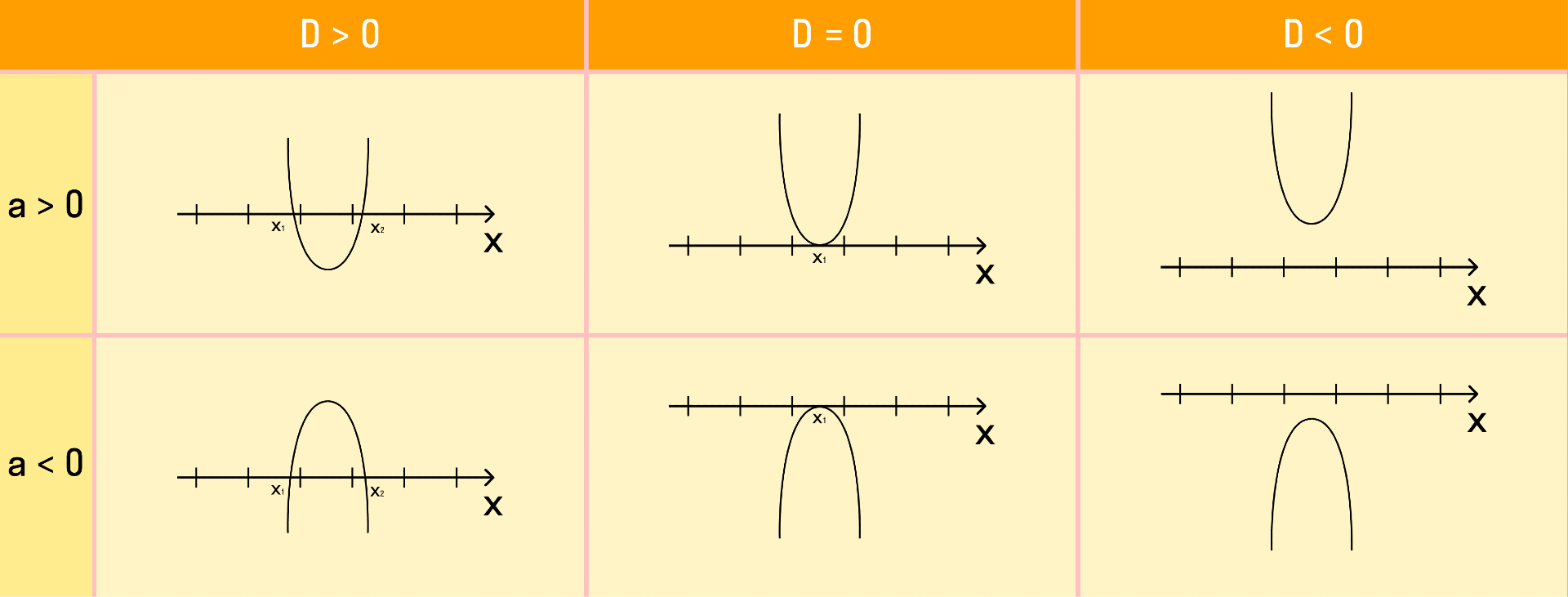
При решении квадратного неравенства необходимо найти корни соответствующего квадратного уравнения ax 2 + bx + c = 0. Чтобы найти корни, нужно найти дискриминант данного уравнения.

Как дискриминант влияет на корни уравнения:

1. D = 0. Если дискриминант равен нулю, тогда у квадратного уравнения есть один корень;
2. D > 0. Если дискриминант больше нуля, тогда у квадратного уравнения есть два различных корня;
3. D 2 + bx + c.

Если требуется найти числовой промежуток, на котором квадратный трехчлен ax 2 + bx + c больше нуля, то этот числовой промежуток находится там, где парабола лежит выше оси ОХ.

Если нужно найти числовой промежуток, на котором квадратный трехчлен ax 2 + bx + c меньше нуля — это числовой промежуток, где парабола лежит ниже оси ОХ.

Если квадратное неравенство нестрогое, то корни входят в числовой промежуток. А если строгое — не входят.

Обучение на курсах по математике в онлайн-школе Skysmart сделает сложные темы понятными, а высокий балл на экзаменах — достижимым!

Видео:КВАДРАТНЫЕ НЕРАВЕНСТВА ПОНЯТНЫМ ЯЗЫКОМСкачать

Решение неравенства методом интервалов

Метод интервалов — это специальный алгоритм, который предназначен для решения рациональных неравенств.

Рациональное неравенство имеет вид f(x) ≤ 0, где f(x) — рациональная функция. При этом знак может быть любым: >, 2 + bx + c из левой части квадратного неравенства.

Изобразить координатную прямую и при наличии корней отметить их на ней.

Если неравенство строгое, нужно отметить корни пустыми (выколотыми) точками. Если нестрогое — обычными точками. Именно эти точки разбивают координатную ось на промежутки.

Если квадратное неравенство со знаком > или ≥ — наносим штриховку над промежутками со знаками +.

Если неравенство со знаком 2 + 4x — 5, его корнями являются числа -5 и 1, они разбивают числовую ось на три промежутка: (-∞, -5), (-5, 1) и (1, +∞).

Определим знак трехчлена x 2 + 4x — 5 на промежутке (1, +∞). Для этого вычислим значение данного трехчлена при некотором значении x из этого промежутка. Можно брать любое значение переменной, главное — чтобы вычисления были простыми. В нашем случае, возьмем x = 2. Подставим его в трехчлен вместо переменной x:

• 2 2 + 4 * 2 — 5 = 4 + 8 — 5 = 7.

7 — положительное число. Это значит, что любое значение квадратного трехчлена на интервале (1, +∞) будет положительным. Так мы определили знак плюс.

Определим знаки на оставшихся двух промежутках. Начнем с интервала (-5, 1). Из этого интервала можем взять x = 0 и вычислить значение квадратного трехчлена при этом значении переменной:

• 0 2 + 4 * 0 — 5 = 0 + 0 — 5 = -5.

Так как -5 — отрицательное число, то на этом интервале все значения трехчлена будут отрицательными. Так мы определили знак минус.

Осталось определиться со знаком на промежутке (-∞, -5). Возьмем x = -6, подставляем:

• (-6) 2 + 4 * (-6) — 5 = 36 — 24 — 5 = 7.

Следовательно, искомый знак — плюс.

Можно расставить знаки быстрее, если запомнить эти факты:

Видео:Решение квадратных неравенств методом интервалов. Практическая часть. 8 класс.Скачать

Плюс или минус: как определить знаки

Можно сделать вывод о знаках по значению старшего коэффициента a:

если a > 0, последовательность знаков: +, −, +,

если a 0, последовательность знаков: +, +,

если a 2 — 7 не имеет корней и на промежутке (−∞, +∞) его значения отрицательны, так как коэффициент при x 2 есть отрицательное число -4, и свободный член -7 тоже отрицателен.

• Когда квадратный трехчлен при D > 0 имеет два корня, то знаки его значений на промежутках чередуются. Это значит, что достаточно определить знак на одном из трех промежутков и расставить знаки над оставшимися промежутками, чередуя их. В результате возможна одна из двух последовательностей: +, −, + или −, +, −.
• Если квадратный трехчлен при D = 0 имеет один корень, то этот корень разбивает числовую ось на два промежутка, а знаки над ними будут одинаковыми. Это значит, что достаточно определить знак над одним из них и над другим поставить такой же. При этом получится, либо +, +, либо −, −.
• Когда квадратный трехчлен корней не имеет (D

Теперь мы знаем пошаговый алгоритм. Чтобы закрепить материал потренируемся на примерах и научимся использовать метод интервалов для квадратных неравенств.

Пример 1. Решить неравенство методом интервалов: x^2 — 5x + 6 ≥ 0.

Разложим квадратный трехчлен на множители.

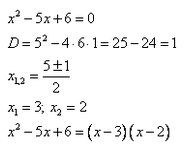
Неравенство примет вид:

Проанализируем два сомножителя:

Первый: х — 3. Этот сомножитель может поменять знак при х = 3, значит при х 0 принимает положительные значения: х — 3 > 0.

Второй: х — 2. Для этого сомножителя такая «знаковая» точка: х = 2.

Вывод: знак произведения (х — 3) * (х — 2) меняется только при переходе переменной через значения х = 3 и х = 2.

В этом весь смысл метода интервалов: определить интервалы значений переменной, на которых ситуация не меняется и рассматривать их как единое целое.

Построим чертеж.

Рассмотрим интервалы в том же порядке, как пишем и читаем: слева направо.

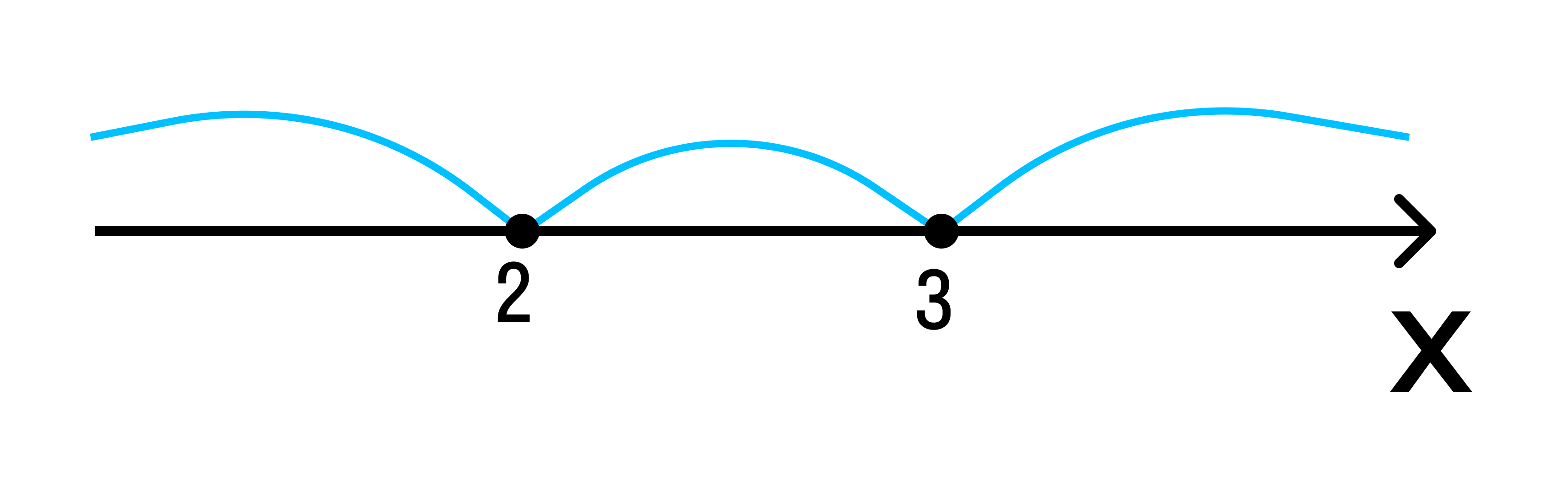
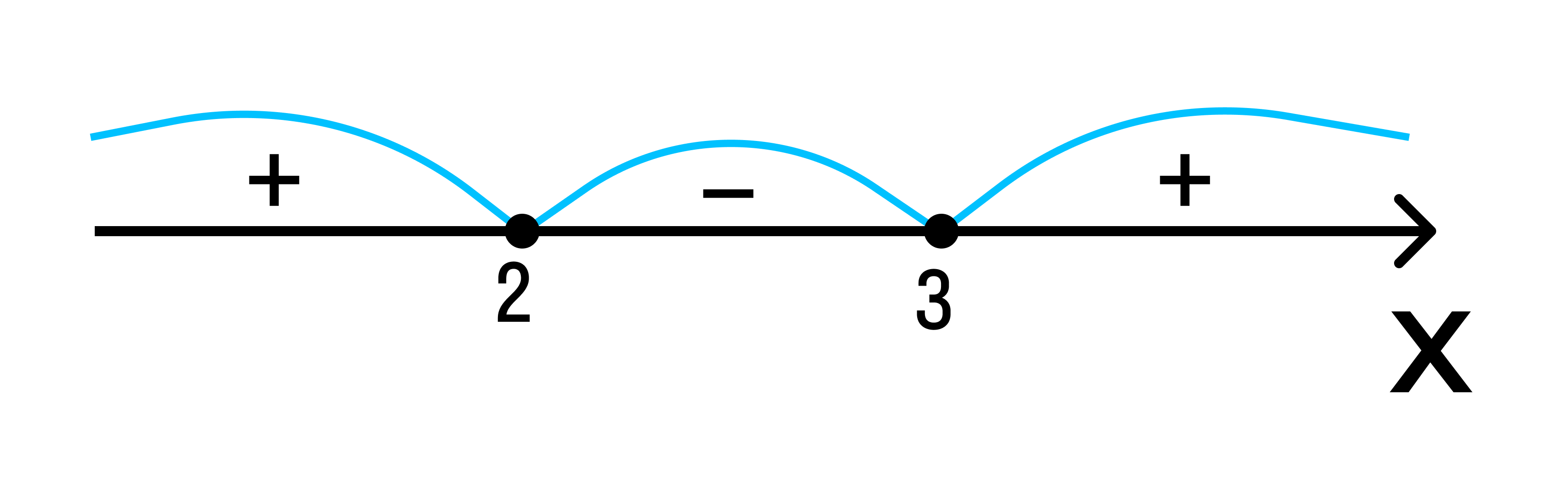
Отобразим эти данные на чертеже:

2 3 — на этом интервале ситуация не изменяется. Значит нужно взять любое значение из этого интервала и подставить его в произведение. Например: х = 25.

• (25 — 3) (25 — 2) = 22*23 = 506 > 0

Вывод: при х > 3 верно неравенство (х — 3) * (х — 2) > 0. Внесем эти данные в чертеж.

Исходное неравенство: (х — 3) * (х — 2) ≥ 0.

Если (х — 3) * (х — 2) > 0:

Если (х — 3) (х — 2) = 0 — при х1 = 3, х2 = 2.

Удовлетворяющие неравенству точки закрасим, а не удовлетворяющие — оставим пустыми.

Ответ: х ≤ 0, х ≥ 3.

Пример 2. Применить метод интервалов для решения неравенства х2+4х+3

Видео:Подготовка к ОГЭ . Рациональные неравенства | Математика | TutorOnlineСкачать

Решение квадратных неравенств методом интервалов.

Метод интервалов является универсальным методом решения неравенств, в частности, он позволяет решать квадратные неравенства с одной переменной. В этой статье мы подробно осветим все нюансы решения квадратных неравенств методом интервалов. Сначала приведем алгоритм, после чего детально разберем готовые решения характерных примеров.

Навигация по странице.

Видео:Решение неравенств методом интервалов. Алгебра, 9 классСкачать

Алгоритм

Первое знакомство с методом интервалов обычно происходит на уроках алгебры, когда учатся решать квадратные неравенства. При этом алгоритм метода интервалов дают в виде, адаптированном именно к решению квадратных неравенств. Отдавая дань простоте, мы тоже дадим его в таком виде, а общий алгоритм метода интервалов Вы можете посмотреть по ссылке в самом начале этой статьи.

Итак, алгоритм решения квадратных неравенств методом интервалов таков:

• Находим нули квадратного трехчлена a·x 2 +b·x+c из левой части квадратного неравенства.
• Изображаем координатную прямую и при наличии корней отмечаем их на ней. Причем если решаем строгое неравенство, то отмечаем их пустыми (выколотыми) точками, а если решаем нестрогое неравенство – то обычными точками. Они разбивают координатную ось на промежутки.
• Определяем, какие знаки имеют значения трехчлена на каждом промежутке (если на первом шаге были найдены нули) или на всей числовой прямой (если нулей нет), как это сделать расскажем чуть ниже. И проставляем над этими промежутками + или − в соответствии с определенными знаками.
• Если решаем квадратное неравенство со знаком > или ≥, то наносим штриховку над промежутками со знаками +, если же решаем неравенство со знаком x 2 +4·x−5 , его корнями являются числа −5 и 1 , они разбивают числовую ось на три промежутка (−∞, −5) , (−5, 1) и (1, +∞) .

Определим знак трехчлена x 2 +4·x−5 на промежутке (1, +∞) . Для этого вычислим значение данного трехчлена при некотором значении x из этого промежутка. Целесообразно брать такое значение переменной, чтобы вычисления были простыми. В нашем случае, например, можно взять x=2 (с этим числом вычисления проводить проще, чем, к примеру, с 1,3 , 74 или ). Подставляем его в трехчлен вместо переменной x , в результате получаем 2 2 +4·2−5=7 . 7 – положительное число, это означает, что любое значение квадратного трехчлена на интервале (1, +∞) будет положительным. Так мы определили знак +.

Для закрепления навыков определим знаки на оставшихся двух промежутках. Начнем со знака на интервале (−5, 1) . Из этого интервала лучше всего взять x=0 и вычислить значение квадратного трехчлена при этом значении переменной, имеем 0 2 +4·0−5=−5 . Так как −5 – отрицательное число, то на этом интервале все значения трехчлена будут отрицательными, следовательно, мы определили знак минус.

Осталось выяснить знак на промежутке (−∞, −5) . Возьмем x=−6 , подставляем его вместо x , получаем (−6) 2 +4·(−6)−5=7 , следовательно, искомым знаком будет плюс.

Но быстрее расставить знаки позволяют следующие факты:

• Когда квадратный трехчлен имеет два корня (при положительном дискриминанте), то знаки его значений на промежутках, на которые эти корни разбивают числовую ось, чередуются (как в предыдущем примере). То есть, достаточно определить знак на одном из трех промежутков, и расставить знаки над оставшимися промежутками, чередуя их. В результате возможна одна из двух последовательностей знаков: +, −, + или −, +, −. Более того, можно вообще обойтись без вычисления значения квадратного трехчлена в точке промежутка, а сделать выводы о знаках по значению старшего коэффициента a: если a>0, то имеем последовательность знаков +, −, +, а если a – то −, +, −.
• Если же квадратный трехчлен имеет один корень (когда дискриминант равен нулю), то этот корень разбивает числовую ось на два промежутка, а знаки над ними будут одинаковыми. То есть, достаточно определить знак над одним из них, а над другим – поставить такой же. При этом получится, либо +, +, либо −, −. Вывод по знакам можно также сделать на основе значения коэффициента a: если a>0 , то будет +, +, а если a , то −, −.
• Когда квадратный трехчлен корней не имеет, то знаки его значений на всей числовой прямой совпадают как со знаком старшего коэффициента a , так и со знаком свободного члена c . Для примера рассмотрим квадратный трехчлен −4·x 2 −7 , он не имеет корней (его дискриминант отрицательный), и на промежутке (−∞, +∞) его значения отрицательны, так как коэффициент при x 2 есть отрицательное число −4 , и свободный член −7 тоже отрицателен.

Теперь все шаги алгоритма разобраны и остается рассмотреть примеры решения квадратных неравенств с его использованием.

Видео:"МАТЕМАТИКА без проблем". Квадратные неравенства, решение методом интервалов.Скачать

Примеры с решениями

Переходим к практике. Решим несколько квадратных неравенств методом интервалов, затронем основные характерные случаи.

📸 Видео

Метод интервалов #1Скачать

ПРОСТЕЙШИЙ метод решения систем квадратных неравенствСкачать

Квадратные неравенства Как решать неравенства методом интервалов?Скачать

Метод интервалов #3Скачать

Как решать неравенства? Математика 10 класс | TutorOnlineСкачать

Решение квадратных неравенств методом интерваловСкачать

УНИВЕРСАЛЬНЫЙ МЕТОД при решении Неравенств — Метод ИнтерваловСкачать

Профильный ЕГЭ 2023. Задача 14. Неравенства. Метод интервалов. 10 классСкачать

Метод интервалов #4 для продвинутыхСкачать

8 класс, 41 урок, Решение квадратных неравенствСкачать