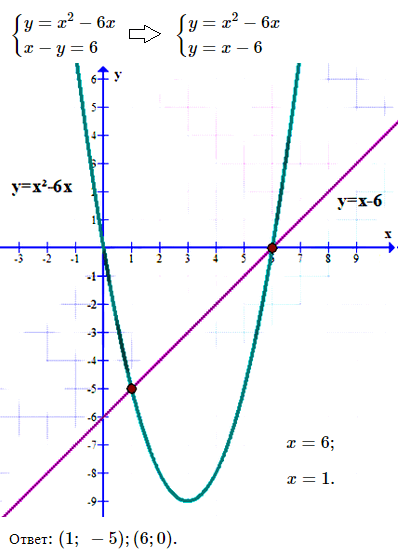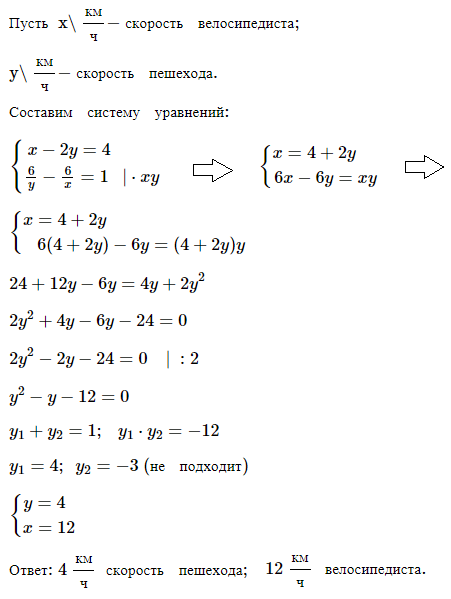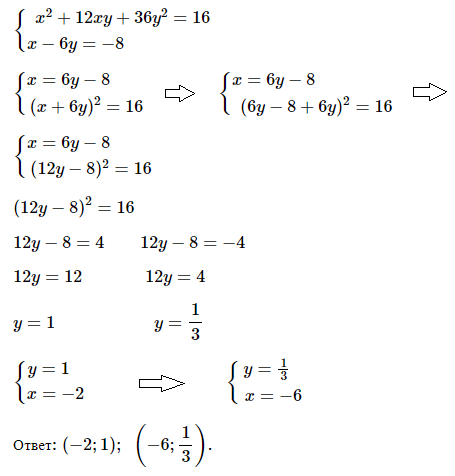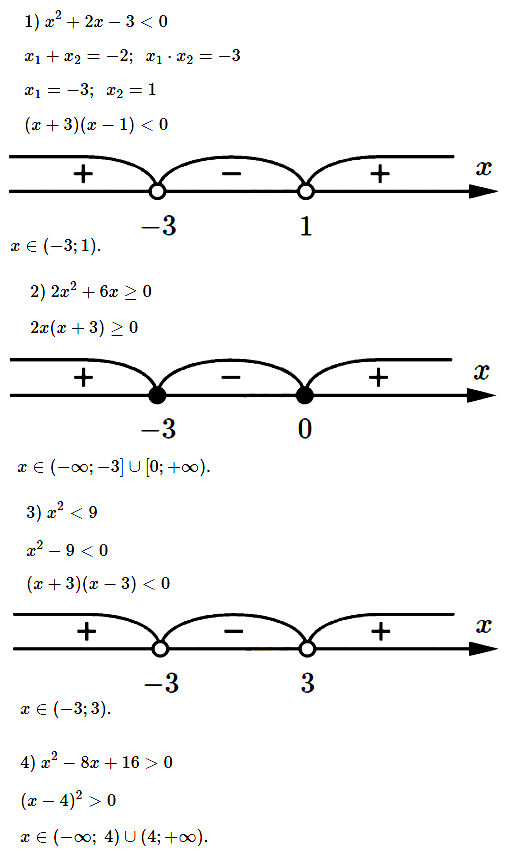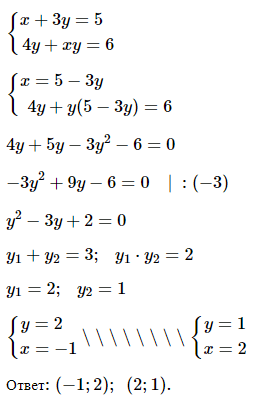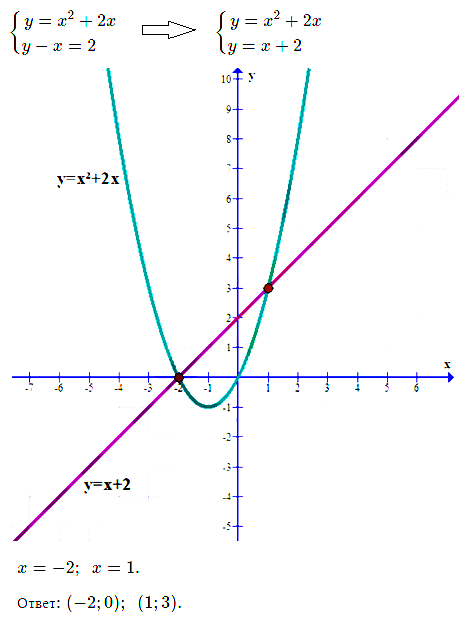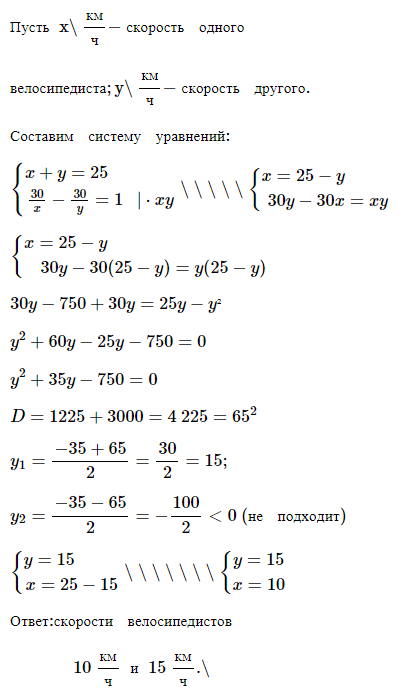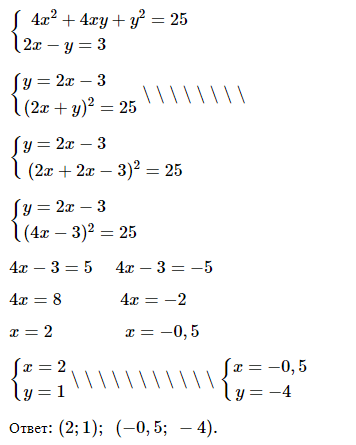Решение квадратных неравенств решение систем уравнений с двумя переменными

Видео:ПРОСТЕЙШИЙ метод решения систем квадратных неравенствСкачать

Мерзляк 9 класс Контрольная 3

Алгебра. Мерзляк 9 класс Контрольная 3 в 4-х вариантах. Контрольная работа по алгебре в 9 классе «Решение квадратных неравенств. Системы уравнений с двумя переменными» для УМК Мерзляк, Полонский, Якир. Транскрипт заданий.

Алгебра 9 класс (УМК Мерзляк)
Контрольная работа № 3

по теме «Решение квадратных неравенств.
Системы уравнений с двумя переменными»

Вариант 1

Вариант 2

1. Решите неравенство: 1) х 2 + 2х – 3 2 + 6х ≥ 0; 3) х 2 2 – 8х + 16 > 0.
2. Решите систему уравнений
   < х + 3у = 5,
   < 4 у + ху = 6.
3. Найдите область определения функции: 1) у = √[3х – х 2 ]; 2) у = 4/√[4 – 8х – 5х 2 ].
4. Решите графически систему уравнений
   < у = х 2 + 2х,
   < y – x = 2.
5. Из двух городов, расстояние между которыми равно 25 км, выехали одновременно навстречу друг другу два велосипедиста и встретились через 1 ч после начала движения. Найдите скорость каждого велосипедиста, если один из них проезжает 30 км на 1 ч быстрее другого.
6. Решите систему уравнений
   < 4х 2 + 4ху + у 2 = 25,
   < 2х – у = 3.

Вариант 3

1. Решите неравенство: 1) х 2 + 3х – 4 > 0; 2) 4х 2 – 8х ≤ 0; 3) х 2 > 4; 4) х 2 – 10х + 25 ≤ 0.
2. Решите систему уравнений
   < у + 2 х = 5,
   < 2х – ху = –1.
3. Найдите область определения функции: 1) у = √[4х – х 2 ]; 2) у = 5/√[5 – 14х – 3х 2 ].
4. Решите графически систему уравнений
   < у = х 2 + 4 х,
   < y – x = 4.
5. Расстояние между двумя посёлками, равное 12 км, первый пешеход проходит на 1 ч быстрее второго. Найдите скорость каждого пешехода, если второй пешеход за 2 ч проходит на 2 км больше, чем первый за 1 ч.
6. Решите систему уравнений
   < 9х 2 – 12ху + 4у 2 = 9,
   < х + 2у = 9.

Вариант 4

1. Решите неравенство: 1) х 2 + 5х – 6 2 + 24х ≥ 0; 3) х 2 2 – 12х + 36 > 0.
2. Решите систему уравнений
   < 2х + у = 4,
   < ху + 2х = –12.
3. Найдите область определения функции:
   1) у = √[7х – х 2 ]; 2) у = 11/√[9 + 7 х – 2х 2 ].
4. Решите графически систему уравнений
   < у = 4х – х 2 ,
   < 2x + y = 5.
5. От двух пристаней, расстояние между которыми равно 50 км, отправились одновременно навстречу друг другу два катера и встретились через 1 ч после начала движения. Найдите скорость каждого катера, если один из них проходит 60 км на 1 ч быстрее другого.
6. Решите систему уравнений
   < 16х 2 + 8ху + у 2 = 36,
   < 3х – у = 8.

Ответы на КР-3 Вариант 1

№ 1. Решите неравенство: 1) х 2 – 4х – 5 > 0; 2) 3х 2 – 12х ≤ 0;
3) х 2 > 16; 4) х 2 – 4х + 4 ≤ 0.

Нажмите на спойлер ниже, чтобы увидеть ОТВЕТЫ на задание.

№ 2. Решите систему уравнений
< х – 5у = 3,
< ху + 3у = 11.

№ 3. Найдите область определения функции: 1) у = √[5х – х 2 ]; 2) у = 6/√[8 + 10х – 3х 2 ].

№ 4. Решите графически систему уравнений
< у = х 2 – 6х,
< х – у = 6.

№ 5. Расстояние между двумя сёлами, равное 6 км, велосипедист проезжает на 1 ч быстрее, чем проходит это расстояние пешеход. Найдите скорость каждого из них, если за 2 ч пешеход проходит на 4 км меньше, чем велосипедист проезжает за 1 ч.

Ответы на КР-3 Вариант 2

№ 1. Решите неравенство: 1) х 2 + 2х – 3 2 + 6х ≥ 0; 3) х 2 2 – 8х + 16 > 0.

№ 2. Решите систему уравнений
< х + 3у = 5,
< 4 у + ху = 6.

№ 3. Найдите область определения функции: 1) у = √[3х – х 2 ]; 2) у = 4/√[4 – 8х – 5х 2 ].

№ 4. Решите графически систему уравнений
< у = х 2 + 2х,
< y – x = 2.

№ 5. Из двух городов, расстояние между которыми равно 25 км, выехали одновременно навстречу друг другу два велосипедиста и встретились через 1 ч после начала движения. Найдите скорость каждого велосипедиста, если один из них проезжает 30 км на 1 ч быстрее другого.

№ 6. Решите систему уравнений
< 4х 2 + 4ху + у 2 = 25,
< 2х – у = 3.

Вы смотрели: Алгебра. Мерзляк 9 класс Контрольная 3 в 4-х вариантах. Контрольная работа по математике в 9 классе «Решение квадратных неравенств. Системы уравнений с двумя переменными» по УМК Мерзляк, Полонский, Якир. Цитаты из пособия «Алгебра 9 класс. Методическое пособие / Е.В. Буцко и др.» использованы в учебных целях.

Видео:Решение системы неравенств с двумя переменными. 9 класс.Скачать

Мерзляк 9 класс Контрольная 3: 4 комментария

Можно было бы получить ответы для проверки?

К сожалению, авторы пособия не указали ответы на свои задания.

2 вариант почему нету

А где 2 вариант?

Добавить комментарий Отменить ответ

Этот сайт использует Akismet для борьбы со спамом. Узнайте, как обрабатываются ваши данные комментариев.

Видео:Решение квадратных неравенств | МатематикаСкачать

Предметы

Видео:Решение квадратных неравенств методом интервалов. 8 класс.Скачать

Новые работы

Видео:РЕШЕНИЕ КВАДРАТНЫХ НЕРАВЕНСТВ. СИСТЕМЫ УРАВНЕНИЙ. Контрольная № 3 Алгебра 9 класс.Скачать

Найти контрольную:

Видео:Система уравнений VS Система неравенств. ОГЭ по математике №9, 13| Математика TutorOnlineСкачать

Авторы работ и УМК

Видео:Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Предметы

Видео:Системы квадратных неравенств и их решение. 8 класс.Скачать

Важные страницы

Соглашение о конфиденциальности

(с) 2020-2022. Дистанционный информационный Центр НПИ (г.Москва). Бесплатная помощь школьникам, находящимся на домашнем или семейном обучении. Цитаты из учебных пособий размещены в учебных целях. Контакты: kip1979@mail.ru

Видео:Как понять неравенства? Квадратные неравенства. Линейные и сложные неравенства | TutorOnlineСкачать

Популярное

Видео:КВАДРАТНЫЕ НЕРАВЕНСТВА ПОНЯТНЫМ ЯЗЫКОМСкачать

Предупреждение

Продолжая использовать наш сайт, вы даете согласие на обработку файлов cookie, пользовательских данных (сведения о местоположении; тип и версия ОС; тип и версия Браузера; тип устройства и разрешение его экрана; источник откуда пришел на сайт пользователь; с какого сайта или по какой рекламе; язык ОС и Браузера; какие страницы открывает и на какие кнопки нажимает пользователь; ip-адрес) в целях функционирования сайта, проведения ретаргетинга и проведения статистических исследований и обзоров. Если вы не хотите, чтобы ваши данные обрабатывались, покиньте сайт.

Видео:Системы неравенств с двумя переменными. Алгебра, 9 классСкачать

Методы решения систем уравнений с двумя переменными

п.1. Метод подстановки

Вариант 1
Шаг 1. Из одного уравнения выразить y через x: y(x).
Шаг 2. Подставить полученное выражение во второе уравнение и найти x.
Шаг 3. Подставить найденный x в y(x) и найти y.
Шаг 4. Записать полученные пары решений. Работа завершена.

Вариант 2
Шаг 1. Из одного уравнения выразить x через y: x(y).
Шаг 2. Подставить полученное выражение во второе уравнение и найти y.
Шаг 3. Подставить найденный y в x(y) и найти x.
Шаг 4. Записать полученные пары решений. Работа завершена.

п.2. Метод сложения

п.3. Метод замены переменных

Иногда удобно ввести новые переменные и решить систему для них.
А затем, вернуться к исходным переменным и найти их значения.

п.4. Графический метод

Графический метод подробно рассмотрен в §15 данного справочника.

п.5. Примеры

Пример 1. Решите систему уравнений:
а) ( left< begin mathrm & \ mathrm & endright. )
Решаем методом подстановки: ( left< begin mathrm & \ mathrm & endright. )
Для нижнего уравнения: ( mathrm )
Подставляем в верхнее уравнение: ( mathrm )

б) ( left< begin mathrm & \ mathrm & endright. )
Замена переменных: ( left< begin mathrm & \ mathrm & endright. )
Выразим (x 2 + y 2 ) через a и b:
x 2 + y 2 = (x 2 + y 2 + 2xy) – 2xy = (x + y) 2 – 2xy = a 2 – 2b
Подставляем: ( left< begin mathrm & \ mathrm & endright.Rightarrow left< begin mathrm & \ mathrm & endright. )
Решаем нижнее уравнение: 2b 2 – 9b + 10 = 0 $$ mathrm< D=9^2-4cdot 2cdot 10=1, b=frac> = left[begin mathrm & \ mathrm & endright. $$ Возвращаемся к исходным переменным: ( left[begin left<begin mathrm & \ mathrm & endright.& \ left<begin mathrm & \ mathrm & endright. endright. )

Видео:Решение систем уравнений второго порядка. 8 класс.Скачать

Системы из линейных и квадратных неравенств

Этот видеоурок доступен по абонементу

У вас уже есть абонемент? Войти

На этом уроке мы продолжим рассмотрение рациональных неравенств и их систем, а именно: систему из линейных и квадратных неравенств. Вначале вспомним, что такое система двух линейных неравенств с одной переменной. Далее рассмотрим систему квадратных неравенств и методику их решения на примере конкретных задач. Подробно рассмотрим так называемый метод крыши. Разберем типовые решения систем и в конце урока рассмотрим решение системы с линейным и квадратным неравенством.

🌟 Видео

Решение систем уравнений второй степени. Алгебра, 9 классСкачать

Неравенства с двумя переменными. Алгебра, 9 классСкачать

9 класс, 11 урок, Методы решения систем уравненийСкачать

9 класс. Урок 3: Решение квадратных неравенств. Системы уравнений с двумя переменнымиСкачать

Решение системы неравенствСкачать

Решение квадратных неравенств графическим методом. 8 класс.Скачать

Решение системы линейных уравнений с двумя переменными способом подстановки. 6 класс.Скачать

Неравенства с двумя переменными. Практическая часть. 9 класс.Скачать