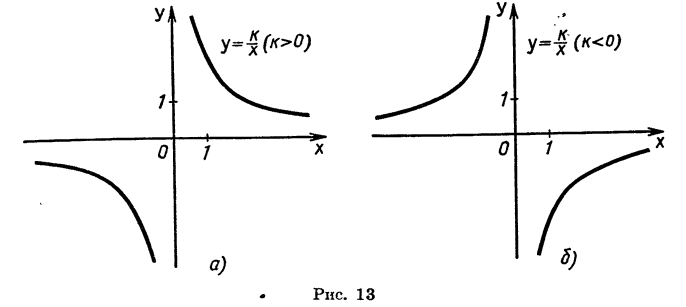
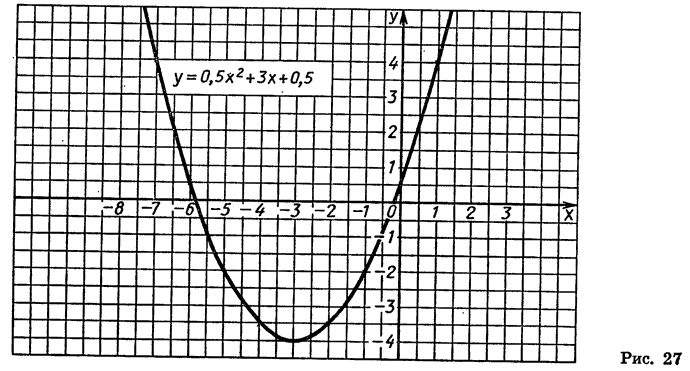
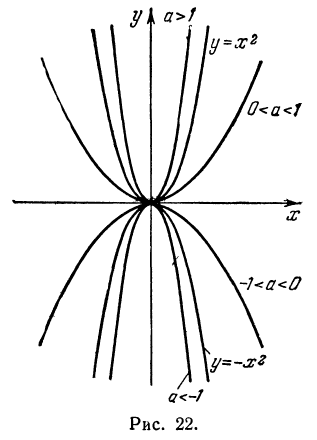
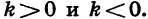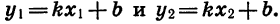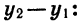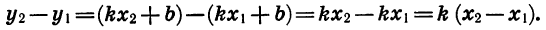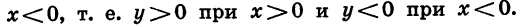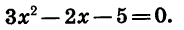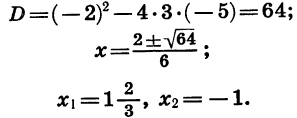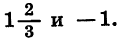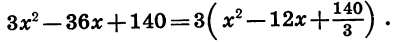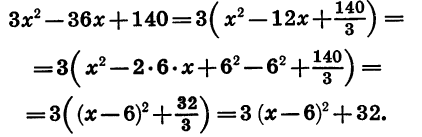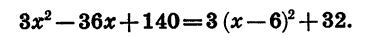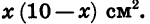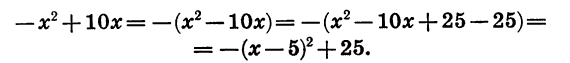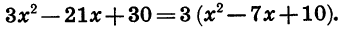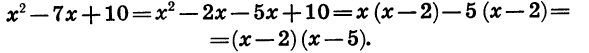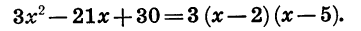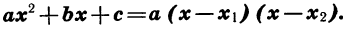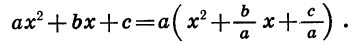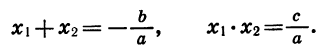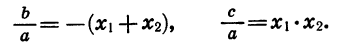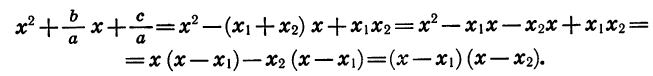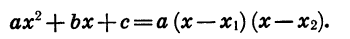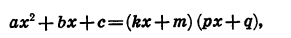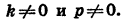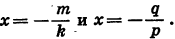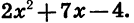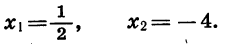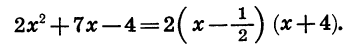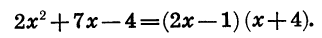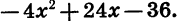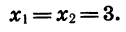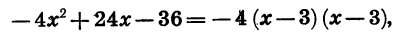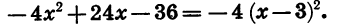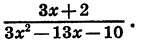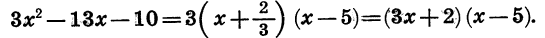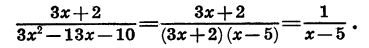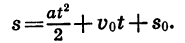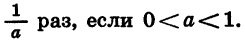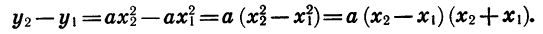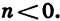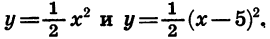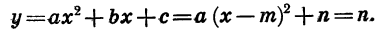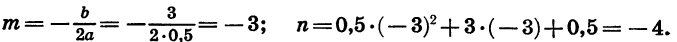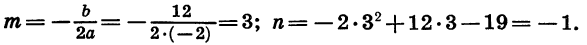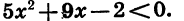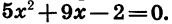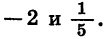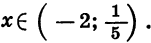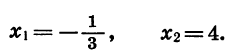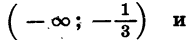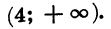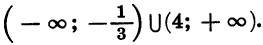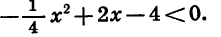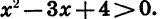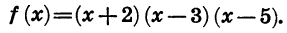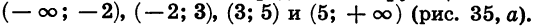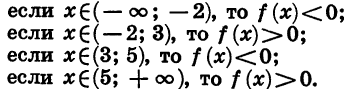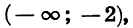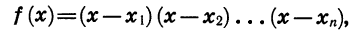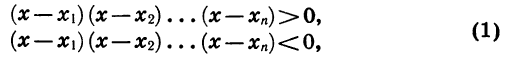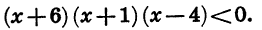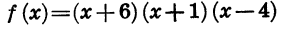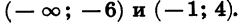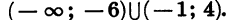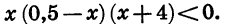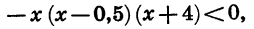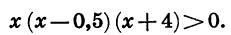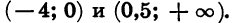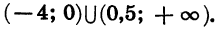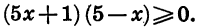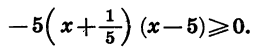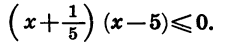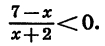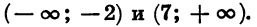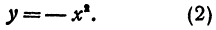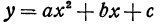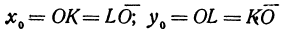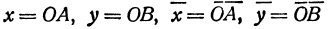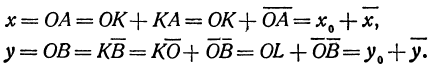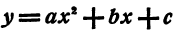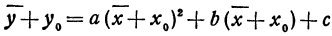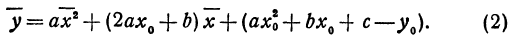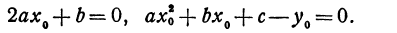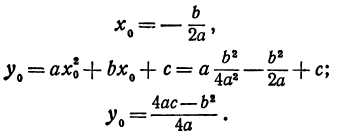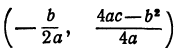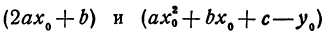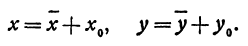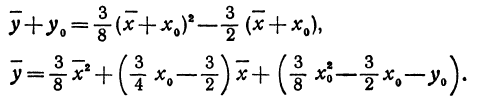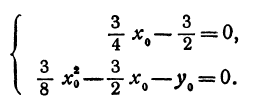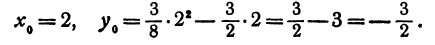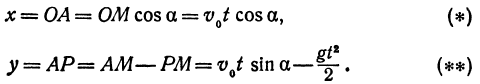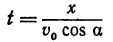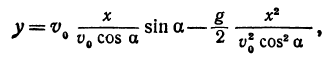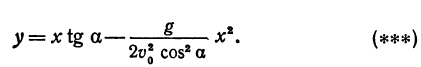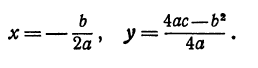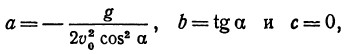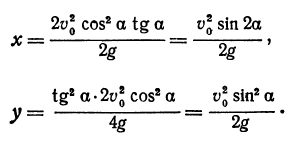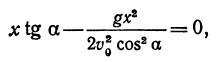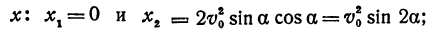В этой статье мы поговорим о том, что такое квадратичная функция, научимся строить ее график и определять вид графика в зависимости от знака дискриминанта и знака старшего коэффициента.
Итак.
Функция вида 


В уравнении квадратичной функции:
a — старший коэффициент
b — второй коэффициент
с — свободный член.
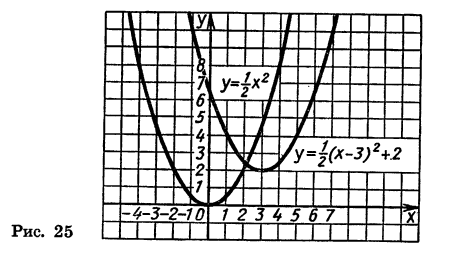
Графиком квадратичной функции является квадратичная парабола, которая для функции 
Обратите внимание на точки, обозначенные зелеными кружками — это, так называемые «базовые точки». Чтобы найти координаты этих точек для функции 
Внимание! Если в уравнении квадратичной функции старший коэффициент 

График функции 
Для нахождения координат базовых точек составим таблицу:
Обратите внимание, что график функции 

Итак, мы заметили:
Если старший коэффициент a>0 , то ветви параболы напрaвлены вверх .
Если старший коэффициент a , то ветви параболы напрaвлены вниз .
Второй параметр для построения графика функции — значения х, в которых функция равна нулю, или нули функции. На графике нули функции 

Поскольку ордината (у) любой точки, лежащей на оси ОХ равна нулю, чтобы найти координаты точек пересечения графика функции 

В случае квадратичной функции 

В процессе решения квадратного уравнения мы находим дискриминант: 
И здесь возможны три случая:
1. Если 




2. Если 




3 . Если 




Если 

Следовательно, зная направление ветвей параболы и знак дискриминанта, мы уже можем в общих чертах определить, как выглядит график нашей функции.
Следующий важный параметр графика квадратичной функции — координаты вершины параболы:
Прямая, проходящая через вершину параболы параллельно оси OY является осью симметрии параболы.
И еще один параметр, полезный при построении графика функции — точка пересечения параболы 
Поскольку абсцисса любой точки, лежащей на оси OY равна нулю, чтобы найти точку пересечения параболы 

То есть точка пересечения параболы с осью OY имеет координаты (0;c).
Итак, основные параметры графика квадратичной функции показаны на рисунке:
Рассмотрим несколько способов построения квадратичной параболы. В зависимости от того, каким образом задана квадратичная функция, можно выбрать наиболее удобный.
1. Функция задана формулой 
Рассмотрим общий алгоритм построения графика квадратичной параболы на примере построения графика функции
1. Направление ветвей параболы.
Так как 

2. Найдем дискриминант квадратного трехчлена

Дискриминант квадратного трехчлена больше нуля, поэтому парабола имеет две точки пересечения с осью ОХ.
Для того, чтобы найти их координаты, решим уравнение:

3. Координаты вершины параболы:
4. Точка пересечения параболы с осью OY: (0;-5),и ей симметричная относительно оси симметрии параболы.
Нанесем эти точки на координатную плоскость, и соединим их плавной кривой:
Этот способ можно несколько упростить.
1. Найдем координаты вершины параболы.
2. Найдем координаты точек, стоящих справа и слева от вершины.
Воспользуемся результатами построения графика функции
Кррдинаты вершины параболы
Ближайшие к вершине точки, расположенные слева от вершины имеют абсциссы соответственно -1;-2;-3
Ближайшие к вершине точки, расположенные справа имеют абсциссы соответственно 0;1;2
Подставим значения х в уравнение функции, найдем ординаты этих точек и занесем их в таблицу:
Нанесем эти точки на координатную плоскость и соединим плавной линией:
2 . Уравнение квадратичной функции имеет вид 

или в уравнении квадратичной функции 
Построим для примера график функции 
Вспомним линейные преобразования графиков функций. Чтобы построить график функции 
- сначала построить график функции
,
- затем одинаты всех точек графика умножить на 2,
- затем сдвинуть его вдоль оси ОХ на 1 единицу вправо,
- а затем вдоль оси OY на 4 единицы вверх:
Теперь рассмотрим построение графика функции 

Выделим в уравнении функции полный квадрат:
Следовательно, координаты вершины параболы: 
3 . Уравнение квадратичной функции имеет вид y=(x+a)(x+b)
Построим для примера график функции y=(x-2)(x+1)
1. Вид уравнения функции позволяет легко найти нули функции — точки пересечения графика функции с осью ОХ:
(х-2)(х+1)=0, отсюда
2. Координаты вершины параболы:
3. Точка пересечения с осью OY: с=ab=(-2)(1)=-2 и ей симметричная.
Нанесем эти точки на координатную плоскость и построим график:
- График квадратичной функции.
- Как определить a, b и c по графику параболы
- 1 способ – ищем коэффициенты на графике
- 3 способ – используем преобразование графиков функций
- Квадратичная (Квадратная) функция и её графики с примерами решения и построения
- Формула корней квадратного уравнения
- Дискриминант
- Трёхчлен второй степени
- Разложение трёхчлена второй степени
- График квадратной функции
- График функции у=x²
- График функции у= x²
- График функции y=ax²+b
- Биквадратное уравнение
- Уравнения, левая часть которых разлагается на множители, а правая есть нуль
- Двучленное уравнение
- Решение двучленных уравнений третьей степени
- Различные значения корня
- Системы уравнений второй степени
- Системы двух уравнений, из которых одно первой степени, а другое—второй
- Система двух уравнений, из которых каждое второй степени
- Графический способ решения систем уравнений второй степени
- Квадратичная функция — основные понятия и определения
- Свойства функции
- Квадратный трехчлен
- Квадратный трехчлен и его корни
- Разложение квадратного трехчлена на множители
- Квадратичная функция и ее график
- Решение неравенств второй степени с одной переменной
- Квадратичная функция и её построение
- Парабола
- Параллельный перенос осей координат
- Исследование функции
- 💡 Видео
График квадратичной функции.
Перед вами график квадратичной функции вида 
Кликните по чертежу.
Подвигайте движки.
Исследуйте зависимость
— ширины графика функции 

— сдвига графика функции 


— сдвига графика функции 
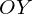

— направления ветвей параболы от знака коэффициента 
— координат вершины параболы 


И.В. Фельдман, репетитор по математике.
Видео:Решение квадратных неравенств графическим методом. 8 класс.Скачать

Как определить a, b и c по графику параболы
Предположим, вам попался график функции (y=ax^2+bx+c) и нужно по этому графику определить коэффициенты (a), (b) и (c). В этой статье я расскажу 3 простых способа сделать это.
Видео:ЭЛЕМЕНТАРНО, ВАТСОН! Квадратичная Функция и ее график ПараболаСкачать

1 способ – ищем коэффициенты на графике
Данный способ хорош, когда координаты вершины и точка пересечения параболы с осью (y) – целые числа. Если это не так, советую использовать способ 2.
Коэффициент (a) можно найти с помощью следующих фактов:
— Если (a>0), то ветви параболы направленных вверх, если (a 1), то график вытянут вверх в (a) раз по сравнению с «базовым» графиком (у которого (a=1)). Вершина при этом остается на месте. Это наглядно видно по выделенным точкам.
Ищем 3 точки с целыми координатами, принадлежащие параболе.
Пример:
Выписываем координаты этих точек и подставляем в формулу квадратичной функции: (y=ax^2+bx+c). Получится система с тремя уравнениями.
Решаем систему.
Пример:
Вычтем из второго уравнения первое:
Подставим (9a) вместо (b):
Первое и второе уравнения совпали (это нормально для точек, симметричных относительно прямой проходящей через вершину – как точки (A) и (B) в нашем случае), но нас это не остановит – мы вычтем из второго уравнение третье:
Подставим в первое уравнение (a):
Получается квадратичная функция: (y=-x^2-9x-15).
Сразу заметим, что по графику можно сразу определить, что (c=4). Это сильно облегчит нашу систему – нам хватит 2 точек. Выберем их на параболе: (C(-1;8)), (D(1;2)) (на самом деле, если присмотреться, то можно заметить, что эти точки выделены жирно на изначальной картинке – это вам подсказка от авторов задачи).
Таким образом имеем систему:
Сложим 2 уравнения:
Подставим во второе уравнение:
Теперь найдем точки пересечения двух функций:
Теперь можно найти ординату второй точки пересечения:
Видео:Квадратичная функция и ее график. 8 класс.Скачать

3 способ – используем преобразование графиков функций
Этот способ быстрее первого и более универсальный, в частности он может пригодится и в задачах на другие функции.
Главный недостаток этого способа — вершина должна иметь целые координаты.
Сам способ базируется на следующих идеях:
График (y=-x^2) симметричен относительно оси (x) графику (y=x^2).
– Если (a>1) график (y=ax^2) получается растяжением графика (y=x^2) вдоль оси (y) в (a) раз.
– Если (a∈(0;1)) график (y=ax^2) получается сжатием графика (y=x^2) вдоль оси (y) в (a) раз.
– График (y=a(x+d)^2) получается сдвигом графика (y=ax^2) влево на (d) единиц.
— График (y=a(x-d)^2) получается сдвигом графика (y=ax^2) вправо на (d) единиц.
График (y=a(x+d)^2+e) получается переносом графика (y=a(x+d)^2) на (e) единиц вверх.
График (y=a(x+d)^2-e) получается переносом графика (y=a(x+d)^2) на (e) единиц вниз.
У вас наверно остался вопрос — как этим пользоваться? Предположим, мы видим такую параболу:
Сначала смотрим на её форму и направленность её ветвей. Видим, что форма стандартная, базовая и ветви направлены вверх, поэтому (a=1). То есть она получена перемещениями графика базовой параболы (y=x^2).
А как надо было перемещать зеленый график чтоб получить оранжевый? Надо сдвинуться вправо на пять единиц и вниз на (4).
То есть наша функция выглядит так: (y=(x-5)^2-4).
После раскрытия скобок и приведения подобных получаем искомую формулу:
Чтобы найти (f(6)), надо сначала узнать формулу функции (f(x)). Найдем её:
Парабола растянута на (2) и ветви направлены вниз, поэтому (a=-2). Иными словами, первоначальной, перемещаемой функцией является функция (y=-2x^2).
Парабола смещена на 2 клеточки вправо, поэтому (y=-2(x-2)^2).
Парабола поднята на 4 клеточки вверх, поэтому (y=-2(x-2)^2+4).
Видео:8 класс, 21 урок, Графическое решение уравненийСкачать

Квадратичная (Квадратная) функция и её графики с примерами решения и построения
Квадратичная функция — целая рациональная функция второй степени вида 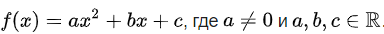
Видео:Решение квадратных уравнений. Дискриминант. 8 класс.Скачать

Формула корней квадратного уравнения
В первой части курса были выведены следующие формулы для определения корней неполного и полного квадратных уравнений:
1) αx²=0; очевидно, оба корня уравнения равны нулю.
2) αx²+с=0; формула для корней будет: 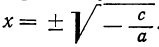
3) αx² +bx=0; тогда x₁ =0; х₂ = 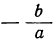
4) x² + +q=0; формула корней даёт:
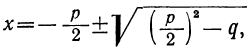
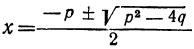
5) Наконец, общая формула для корней полного квадратного уравнения вида αx²+bx+c=0 будет:
Последняя формула является наиболее общей; из неё как частные случаи получаются все остальные. Так, полагая в этой формуле α=l, получаем случай (4) (в этом случае b=p и c=q); полагая с=0, получаем случай (3); при b=0 будем иметь случай (2) и, наконец, первый случай получим, давая в общей формуле значения b=c=0.
Дискриминант
Рассмотрим различные случаи, которые могут встретиться при решении квадратного уравнения в зависимости от числового значения коэффициентов.
1. b² — 4αc>0. В этом случае выражение под корнем положительно. Квадратный корень из него имеет два значения, и, следовательно, уравнение имеет два различных вещественных корня:
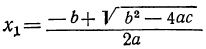
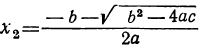
2. b² — 4αc=0. В этом случае второй член числителя равен нулю, и уравнение имеет два равных корня:
3. b² — 4αc Свойства корней квадратного уравнения (теорема Виета)
Возьмём формулу корней квадратного уравнения, у которого коэффициент при x² равен единице, т. е. уравнения вида x²+ +q=0:
Если сложим почленно эти равенства, то радикалы взаимно уничтожатся, и мы получим:
Если те же равенства почленно перемножим, то получим (произведение суммы двух чисел на их разность равно разности квадратов этих чисел):
Каково бы ни было подкоренное число, всегда
Следовательно:
Таким образом:
Сумма корней приведённого квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение этих корней равно свободному члену.
Теперь возьмём квадратное уравнение общего вида αx²+bx+c=0. Разделив все его члены на а, мы приведём это уравнение к только что рассмотренному виду:
следовательно, для неприведённого полного уравнения мы должны иметь:
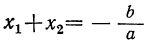
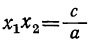
Следствия:
1) Пользуясь этими свойствами, мы легко можем составить квадратное уравнение, у которого корнями были бы данные числа.
Пусть, например, надо составить уравнение, у которого корни были бы числа 2 и 3. Тогда из равенства 2+3= — р и 2∙3 = q находим: р = — 5 и q=6; следовательно, уравнение будет: x²-5x+6=0.
Подобно этому найдём,что 3 и -7 будут корни уравнения x²- [3+(- 7)]x+3( -7) = 0, т. е. x²+4x-21=0; числа 3 и 0 будут корни уравнения x²— 3x=0.
2) При помощи тех же свойств мы можем, не решая квадратного уравнения, определить знаки его корней, если эти корни вещественные. Пусть, например, имеем уравнение x²+8x+12=0. Так как в этом примере выражение 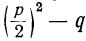
Трёхчлен второй степени
Выражение αx²+bx+c, в котором х означает независимое переменное, а α, b и с — какие-нибудь данные, постоянные числа, называется квадратной функцией, или трёхчленом второй степени. Различие между таким трёхчленом и левой частью уравнения αx²+bx+c=0 состоит в том, что в уравнении буква х означает только те числа, которые удовлетворяют уравнению, тогда как в трёхчлене она означает какое угодно число. Значения х, обращающие трёхчлен в нуль, называются его корнями; значит, корни трёхчлена-это корни квадратного уравнения:
αx² +6x+c=0.
В частном случае при α=1 трёхчлен принимает вид: x²+ +q; при b=0 или при с=0 трёхчлен обращается в двучлен αx²+c или αx²+bx.
Разложение трёхчлена второй степени
Сначала возьмём трёхчлен x²+ +q, в котором коэффициент при x² есть 1. Решив приведённое уравнение x²+ +q=0, мы найдём корни его х₁ и х₂ . Как мы сейчас видели: х₁+х₂ =-p и х₁х₂ =q.
Таким образом:
Трёхчлен x² +q разлагается на два множителя, из которых первый равен разности между х и одним корнем трёхчлена, а второй равен разности между х и другим корнем трёхчлена.
Примеры:
Теперь возьмём трёхчлен αx²+bx+c, в котором коэффициент при x² есть какое угодно число. Этот трёхчлен можно представить так:
Выражение, стоящее внутри скобок, есть трёхчлен вида x²+ +q . Его корни х₁ и х₂ будут те же самые, что трёхчлена αx²+bx+c. Найдя их, мы можем, по доказанному, разложить этот трёхчлен так: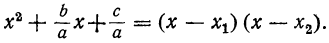
Следовательно: αx²+bx+c =α(x — х₁) (х — х₂).
Таким образом, разложение трёхчлена αx²+bx+c отличается от разложения трёхчлена x²+ +q только дополнительным множителем α.
Примеры:
1) Трёхчлен 2x² — 2х -12, корни которого 3 и — 2, можно разложить так: 2(x — 3)(x+2).
2) Трёхчлен 3x² + х +1, корни которого следующие:
разлагается так:
3) 6abx² — ( 3b³ +2α³)x+a²b² .
Корни этого трёхчлена следующие:
Поэтому:
4) Сократить дробь:
Разложим числитель и знаменатель на множители и затем, если можно, сократим дробь. Так как корни числителя 3 и —2, а корни знаменателя 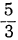
Следствие:
По данным корням можно составить квадратное уравнение. Так, уравнение, имеющее корни З и -2, будет:
(x-3)[x-( — 2)] =0, т. е. (х — 3)(x+2)=0,
что по раскрытии скобок даёт: x² — х — 6 = 0. Конечно, все члены этого уравнения можно умножить на произвольное число, не зависящее от х (например, на 2), отчего корни не изменятся.
Сократить следующие дроби (предварительно разложив числитель и знаменатель каждой дроби на множители):
Разложив на множители следующие трёхчлены, определить, для каких значений х эти трёхчлены будут давать положительные числа и для каких — отрицательные:
Видео:Построение графика квадратичной функцииСкачать

График квадратной функции
Графиком квадратичной функции является парабола.
График функции у=x²
Обратим внимание на следующие особенности функции y=x²;
а) При всяком значении аргумента х функция определена и получает только одно значение. Например, при x = — 10 значение функции будет (-10)² = 100, при x = 1000 значение функции будет 1000² = 1 000 000 и т. п.
б) Так как (—x)² =x² , то при двух значениях х, отличающихся только знаками, получаются два одинаковых положительных значения у; например, при х = — 2 и при x =+2 значение у будет одно и то же, именно 4. Отрицательных значений для у никогда не получается.
в) Если абсолютная величина х неограниченно увеличивается, то и у неограниченно увеличивается. Так, если для х будем давать ряд неограниченно возрастающих положительных значений: 1, 2, 3, 4,… или ряд неограниченно убывающих отрицательных значений: -1, -2, -3, -4, … ,то для у получим ряд неограниченно возрастающих значений: 1, 4, 9, 16, 25, … .
Заметив эти свойства, составим таблицу значений функции у= x²; например, такую:
| x | … | -2 | -1,5 | -1 | -0,5 | 0 | 0,5 | 1 | 1,5 | 2 | … |
| у | … | 4 | 2,25 | 1 | 0,25 | 0 | 0,25 | 1 | 2,25 | 4 | … |
Изобразим теперь эти значения на чертеже 16 в виде точек, абсциссы которых будут выписанные значения х, а ординаты — соответствующие значения у (на чертеже за единицу длины мы приняли отрезок O1); полученные точки соединим кривой. Кривая эта называется параболой. Рассмотрим некоторые её свойства:
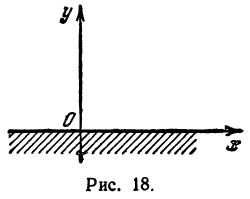
а) Вся кривая расположена по одну сторону от оси х-ов, именно — по ту сторону, по какую лежат положительные значения ординат.
б) Парабола разделяется осью у-ов на две части (ветви). Точка О, в которой эти ветви сходятся, называется вершиной параболы. Эта точка есть единственная общая точка параболы и оси х-ов.
в) Обе ветви бесконечны, так как х и у могут увеличиваться беспредельно. Ветви поднимаются от оси х-ов неограниченно вверх, удаляясь в то же время неограниченно от оси у-ов вправо и влево.
г) Ось у-ов служит для параболы осью симметрии, так что если перегнуть чертёж по этой оси так, чтобы левая половина чертежа упала на правую, то обе ветви совместятся; например, точка с абсциссой — 2 и с ординатой 4 совместится с точкой, имеющей абсциссу +2 и ту же ординату 4.
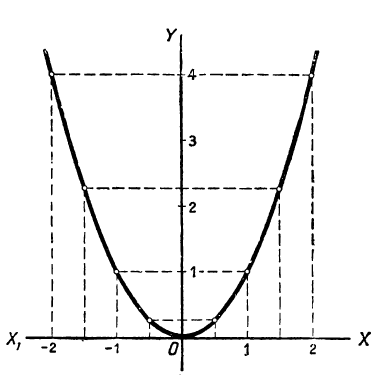
График функции у= x²
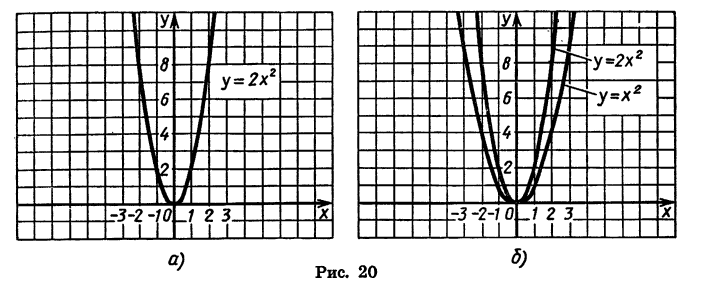
Предположим сначала, что а есть число положительное. Возьмём, например, такие две функции:
Составим таблицы значений этих функций, например такие:
| x | -2 | -1 | 0 | 1 | 2 | … |
| у | 6 | 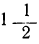 | 0 | 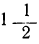 | 6 | … |
| x | -3 | -2 | -1 | 0 | 1 | 2 | … |
| у | 3 | 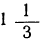 | 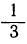 | 0 | 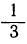 | 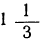 | … |
Нанесём все эти значения на чертёж 17 и проведём кривые. Для сравнения мы поместили на том же чертеже (прерывистой линией) ещё график функции: 3) y=x² .
| x | -2 | -1 | 0 | 1 | 2 | … |
| y | 4 | 1 | 0 | 1 | 4 | … |
Из чертежа видно, что при одной и той же абсциссе ордината первой кривой в 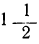
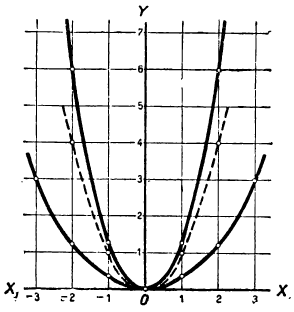
Замечание:
Если зависимость между двумя переменными величинами у и х выражается равенством y=ax² , где a — какое-нибудь постоянное число, то можно сказать, что величина у пропорциональна квадрату величины х, так как с увеличением или уменьшением х в 2 раза, в 3 раза и т. д. величина у увеличивается или уменьшается в 4 раза, в 9 раз, в 16 раз и т. д.
Например, площадь круга равна πR² , где R есть радиус круга и π — постоянное число; поэтому можно сказать, что площадь круга пропорциональна квадрату его радиуса.
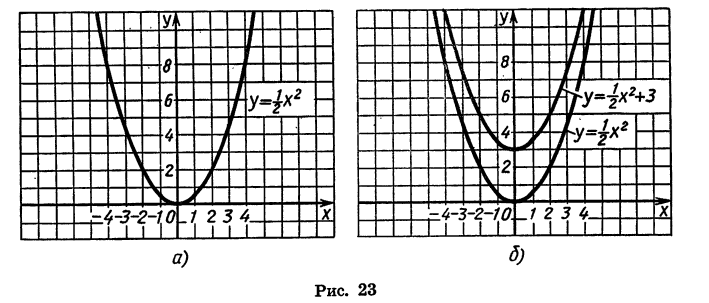
График функции y=ax²+b
Пусть мы имеем следующие три функции:
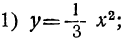
Очевидно, что при одном и том же значении аргумента х ордината второй функции больше, а ордината третьей функции меньше на 2 единицы, чем соответствующая ордината первой функции. Поэтому вторая и третья функции изобразятся на чертеже той же параболой, что и первая функция, только парабола эта должна быть поднята вверх (для второй функции) и опущена вниз (для третьей функции) на 2 единицы длины.
Вообще график функции y=ax²+b есть та же парабола, которая изображает функцию у=ax², только парабола эта должна быть поднята вверх, если b>0, опущена вниз, если b График трёхчлена второй степени
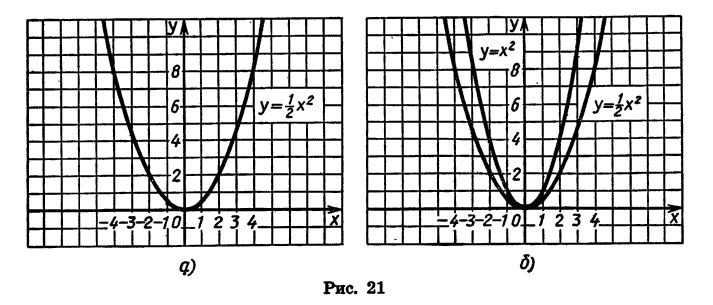
Сначала мы рассмотрим график такого трёхчлена, который может быть представлен в виде произведения a (x+m)² . Например, возьмём такие две функции:
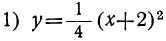
Для сравнения изобразим на том же чертеже ещё параболу:
Предварительно составим таблицу частных значений этих трёх функций; например, такую:
| x= | -5 | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
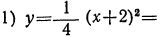 | 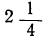 | 1 | 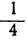 | 0 | 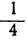 | 1 | 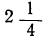 | 4 | 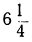 | 9 | 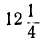 | 16 |
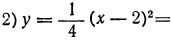 | 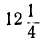 | 9 | 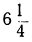 | 4 | 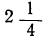 | 1 | 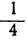 | 0 | 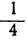 | 1 | 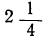 | 4 |
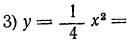 | 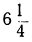 | 4 | 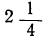 | 1 | 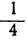 | 0 | 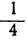 | 1 | 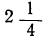 | 4 | 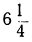 | 9 |
Нанеся все эти значения на чертёж, получим три графика, изображённые на чертеже 19.
Рассматривая этот чертёж, мы замечаем, что кривая 1 есть та же парабола 3, только перенесённая на 2 единицы влево, а кривая 2 есть та же парабола 3, но перенесённая на 2 единицы вправо.
Обобщая этот вывод, мы можем сказать, что график функции y=a(x+m)² есть парабола, изображающая функцию y=ax² , только парабола эта перенесена влево, если m>0, и в правд, если m 0, как в наших примерах, и вниз, если α Графический способ решения квадратного уравнения
Квадратное уравнение можно графически решить таким способом:
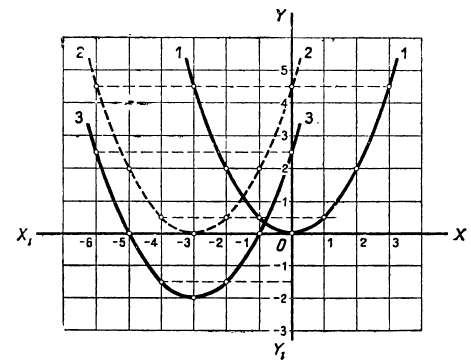
построив на миллиметровой бумаге параболу, изображающую трёхчлен, стоящий в левой части уравнения, находим точки пересечения этой параболы с осью х-ов. Абсциссы этих точек и будут корни уравнения, так как при этих абсциссах ординаты, изображающие соответствующие значения трёхчлена, равны нулю.
Примеры:
График левой части этого уравнения изображён кривой 3 (черт. 20). На нём мы видим, что парабола пересекается с осью х-ов в двух точках, абсциссы которых —1 и —5. Это и будут корни уравнения.
Это можно проверить, решив уравнение посредством общей формулы или путём подстановки.
Составив таблицу частных значений трёхчлена
| x | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | … |
| y | 8 | 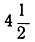 | 2 | 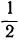 | 0 | 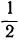 | 2 | 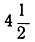 | 8 | … |
мы построим параболу (черт. 21). Эта парабола не пересекается с осью х-ов, а только её касается в точке с абсциссой 2. Уравнение в этом случае имеет только один корень 2 (точнее, два равных корня).
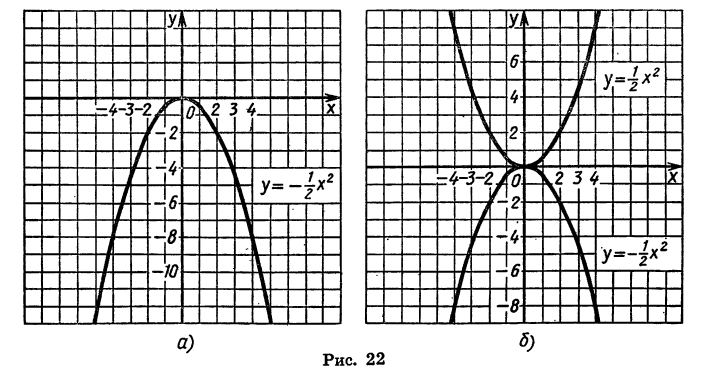
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | … |
| y | 14 | 8 | 4 | 2 | 2 | 4 | 8 | 14 | … |
Парабола (черт. 22) не пересекается и не касается оси х-ов; уравнение не имеет вещественных корней.
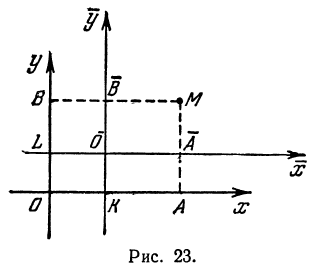
Укажем ещё следующий приём графического решения квадратного уравнения. Пусть требуется решить уравнение:
x² — 1,5х — 2=0.
Каждая часть этого уравнения, рассматриваемая отдельно, есть некоторая функция от х. Обозначим функцию, выражаемую левой частью уравнения, буквой y₁ , а функцию, выражаемую правой частью уравнения, буквой у₂ . Первая функция на чертеже 23 изобразится параболой, а вторая — прямой. Построив на одном и том же чертеже графики этих двух функций, мы найдём, что прямая и парабола пересекаются в двух точках, абсциссы которых приблизительно выражаются числами 2,35 и — 0,85. Это и будут приближённые значения корней данного уравнения, так как при каждой из этих абсцисс ординаты y₁, у₂ равны между собой, и, следовательно, x² =l,5x+2.
Если случится, что прямая с параболой не пересекается, то уравнение не имеет вещественных корней; если же прямая коснётся параболы, то уравнение имеет один корень, равный абсциссе точки касания.
Биквадратное уравнение
Уравнение четвёртой степени, например такое:
x⁴ — 13x² + 36=0,
в которое входят только чётные степени неизвестного, называется биквадратным. Оно приводится к квадратному, если заменим х² через у и, следовательно, x⁴ через у² ; тогда уравнение обратится в квадратное:
у² — 13y+36=0.
Решим его:
Но из равенства x²=y видно, что x=± √y. Подставляя сюда на место у найденные числа 9 и 4, получим следующие четыре решения данного уравнения:
x₁ = +√ 9 = 3;
x₂ = -√ 9 = -3;
x₃ = + √4 =2;
x₃ = — √4 = -2.
Составим формулы для решения биквадратного уравнения общего вида:
ax⁴ +bx² + c=0.
Положив x²=y, получим уравнение ay² + by + c=0, из которого находим:
Но так как x=± √y , то для биквадратного уравнения мы получим следующие четыре решения:
Отсюда видно, что если b² — 4ac 0, то могут быть три случая (мы полагаем a > 0):
1) все корни вещественные (как в приведённом выше численном примере), если 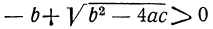
2) все корни мнимые, если оба эти выражения дадут отрицательные числа, и 3) два корня вещественные и два мнимые, если 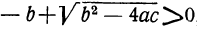
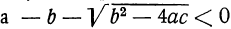
Уравнения, левая часть которых разлагается на множители, а правая есть нуль
Решение таких уравнений сводится к решению уравнений более низких степеней. Так, мы видели, что для решения неполного квадратного уравнения вида ax² + bx=0 достаточно его левую часть разложить на два множителя: x(ax + b) = 0 и затем, приняв во внимание, что произведение равно нулю только тогда, когда какой-нибудь сомножитель равен нулю, свести решение этого уравнения к решению двух уравнений первой степени: x=0 и ax + b=0.
Подобно этому можно решить неполное кубическое уравнение, не содержащее свободного члена; например, такое:
x³ + 3x² — 10x = 0.
Вынеся х за скобки, мы представим уравнение так:
x (x² +3x — 10) = 0,
из которых находим три решения:
Пусть некоторое уравнение приведено к такому виду:
x(x+4)(x²-5x+6)=0.
Тогда оно распадается на три уравнения:
x = 0; x + 4 = 0; x² — 5x + 6 = 0
Двучленное уравнение
Двучленным уравнением называется уравнение вида 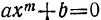
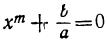
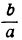
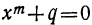
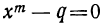
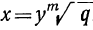
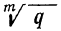
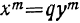
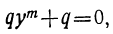
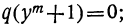
или
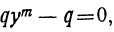
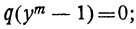
Итак, решение двучленных уравнений приводится к решению уравнений вида 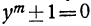
Решение двучленных уравнений третьей степени
Эти уравнения следующие: х³ —1=0 и х³ + l=0.
мы можем предложенные уравнения записать так:
(х -1)(x² + х +1) = 0 и ( х +1 ) ( x² — х +1)=0.
Значит, первое из них имеет своими корнями корни уравнений: x-1=0 и x²+ x +1=0, а второе — корни уравнений: x+1=0 и x²- x +1=0.
Решив их, находим, что уравнение х³ — 1=0 имеет следующие три корня:
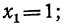
из которых один вещественный, а два мнимых; уравнение х³ + 1 = 0 имеет три корня:

из которых также один вещественный и два мнимых.
Различные значения корня
Решение двучленных уравнений имеет тесную связь с нахождением всех значений корня (радикала) из данного числа. В самом деле, найти 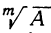
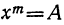
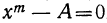
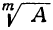
Основываясь на этом замечании, покажем, например, что корень кубичный из всякого вещественного числа (не равного нулю) имеет три различных значения.
Рассмотрим сначала случай положительного числа А. Пусть требуется найти 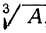
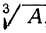
Мы видели, что это уравнение имеет три
корня: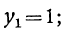
Каждое из этих значений, удовлетворяя уравнению y³ = l, представляет собой кубичный корень из 1. Так как x=qy, то
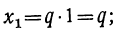
Это и будут три значения 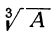
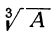
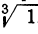
Например, кубичный корень из 8 имеет три следующих значения:
Если A Трёхчленное уравнение
Так называется уравнение вида: 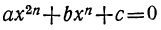
(частный случай такого вида при n=2 есть биквадратное уравнение). Оно приводится к квадратному, если введём вспомогательное неизвестное 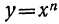
ay²+by+c=0,
откуда:
Следовательно:
Решив, если возможно, это двучленное уравнение, найдём все значения х.
Пример:
x⁶- 9x³ + 8=0.
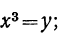
y₁=8; y₂=1;
следовательно:
x³=8 и x³=1.
Решив эти двучленные уравнения третьей степени, получим шесть значений для х:
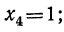
Видео:5 способов решения квадратного уравнения ➜ Как решать квадратные уравнения?Скачать

Системы уравнений второй степени
Степень уравнения с несколькими неизвестными: Чтобы определить степень уравнения, в которое входят несколько неизвестных, надо предварительно это уравнение упростить (раскрыть скобки, освободить от радикалов и знаменателей, которые содержат неизвестные, и сделать приведение подобных членов). Тогда степенью уравнения называется сумма показателей при неизвестных в том члене уравнения, в котором эта сумма наибольшая.
Например, три уравнения: x²+2xy—x+2=0, 3xy=4, 2x+y² — у=0 будут уравнениями второй степени с двумя неизвестными; уравнение 3x²y—y² + x+10 = 0 есть уравнение третьей степени (с двумя неизвестными) и т. п.
Заметим, что сумма показателей при неизвестных в каком-нибудь члене уравнения называется его измерением. Так, члены 2xy, 5x² , Зу² — второго измерения, члены 0,2x²y, 10xy² , 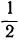
Заметим ещё, что уравнение называется однородным, если все его члены — одного и того же измерения. Так, 3x² + xy — 2y²=0 есть однородное уравнение второй степени с двумя неизвестными.
Мы рассмотрим сейчас, как решаются некоторые простейшие системы уравнений второй степени с двумя неизвестными.
Общий вид полного уравнения второй степени с двумя неизвестными есть следующий:
ax² +bxy+cy² +dx+ey+j=0.
В нём первые три члена — второго измерения, следующие два члена — первого и последний (свободный) член — нулевого. Коэффициенты а, b, с, … могут быть числами положительными, отрицательными, а также равными нулю (конечно, три коэффициента а, b и с не предполагаются одновременно равными нулю, так как в противном случае уравнение было бы не второй, а первой степени).
Мы рассмотрим сейчас, как решаются простейшие системы двух уравнений второй степени с двумя неизвестными.
Системы двух уравнений, из которых одно первой степени, а другое—второй
Пусть дана система:
Всего удобнее такую систему решить способом подстановки следующим путём. Из уравнения первой степени определяем одно какое-нибудь неизвестное как функцию от другого неизвестного; например, определяем у как функцию от х:
y=2x — 1.
Тогда уравнение второй степени после подстановки даёт уравнение с одним неизвестным х:
x² — 4(2x — l)² + x +3(2x — 1) = 1;
x² — 4(4x² — 4x + l)+x+6x— 3=1;
x² — 16x² +16x — 4 + x + 6x — 3 — 1=0;
— 15 x² — 23x-8=0; 15x² — 23x + 8=0;
После этого из уравнения у=2х — 1 находим:
Таким образом, данная система имеет два решения:
Искусственные приёмы:
Указанный приём применим в тех случаях, когда одно уравнение первой степени; в некоторых случаях можно пользоваться искусственными приёмами, для которых нельзя указать общего правила. Приведём примеры.
Пример:
Первый способ. Так как даны сумма и произведение неизвестных, то х и у должны быть корнями квадратного уравнения:
z² — az + b =0.
Следовательно:
Второй способ. Возвысим первое уравнение в квадрат и вычтем из них учетверённое второе:
x²+ 2xy + y² = a²
т.е.
(x-y)² =a²— 4b, откуда
Теперь мы имеем систему:
Складывая и вычитая эти уравнения, получим:
Так как одно из данных уравнений мы возвышали в квадрат, то проверяем подстановкой, нет ли посторонних корней в числе найденных.
Таким образом находим, что данная система имеет два решения:
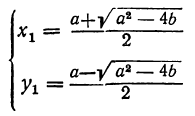
Второе решение отличается от первого только тем, что значение х в первом решении служит значением у во втором решении, и наоборот. Это можно было предвидеть, так как данные уравнения не изменяются от замены х на у, а у на х. Заметим, что такие уравнения называются симметричными.
Пример:
х — y= a, xy=b.
Первый способ. Представив уравнения в виде:
x +( —y)=а, x (-y)=-b,
замечаем, что х и —у это корни квадратного уравнения:
z² -az-b=0,
следовательно:
Второй способ. Возвысив первое уравнение в квадрат и сложив его с учетверённым вторым, получим:
(x + y)² = α² + 4b, откуда
Теперь имеем систему:
Пример:
x+y=cz, x² + y² = 6.
Возвысив первое уравнение в квадрат и вычтя из него второе, получим:
2xy= a² — b, откуда
Теперь вопрос приводится к решению системы:
x + y= a,
которую мы уже рассмотрели в первом примере.
Система двух уравнений, из которых каждое второй степени
Такая система в общем виде не разрешается элементарно, так как она приводится к полному уравнению четвёртой степени.
Рассмотрим некоторые частные виды уравнений, которые можно решить элементарным путём.
Пример:
x² +y² =α, ху=b.
Первый способ (способ подстановки). Из второго уравнения определяем одно неизвестное в зависимости от другого; например, 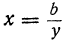
у⁴ — αy² + b² =0.
Решив его, найдём для у четыре значения. Подставив каждое из них в формулу, выведенную ранее для х, найдём четыре соответствующих значения для х.
Второй способ. Сложив первое уравнение с удвоенным вторым, получим:
x² +y² +2xy=α+2b, т. е. (x + y)² =a + 2b,
откуда:
откуда:
Таким образом, вопрос приводится к решению следующих четырёх систем первой степени:
Каждая из них решается весьма просто посредством алгебраического сложения уравнений.
Третий способ. Возвысив второе уравнение в квадрат, получим следующую систему:
x² + y² =α, x²y² =b².
Отсюда видно, что x² и y² — корни квадратного уравнения:
z² + az+b² =0.
Следовательно:
Пример:
x² — y² = a, xy=b.
Способом подстановки легко приведём эту систему к биквадратному уравнению. Вот ещё искусственный’приём решения этой системы.
Отсюда видно, что x² и — y² будут корнями уравнения:
z² — az — b² = 0.
Следовательно:
Замечание:
Во всех случаях, когда приходится возводить уравнения в степень, необходима проверка корней.
Графический способ решения систем уравнений второй степени
Начертив графики каждого из данных уравнений, находим величины координат точек пересечения этих графиков; это и будут корни уравнений.
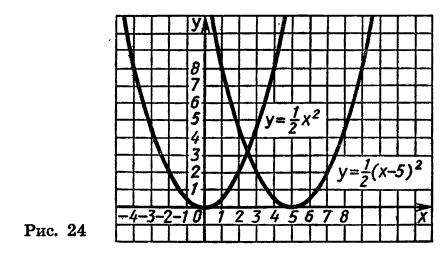
Пример:
Составим таблицу частных значений х и у для первого уравнения:
| x | … | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 | … |
| y | … | 20 | 12 | 6 | 2 | 0 | 0 | 2 | 6 | 12 | … |
и таблицу частных значений х и у для второго уравнения:
| x | … | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | … |
| y | … | 15 | 5 | -1 | -3 | -1 | 5 | 15 | 29 | … |
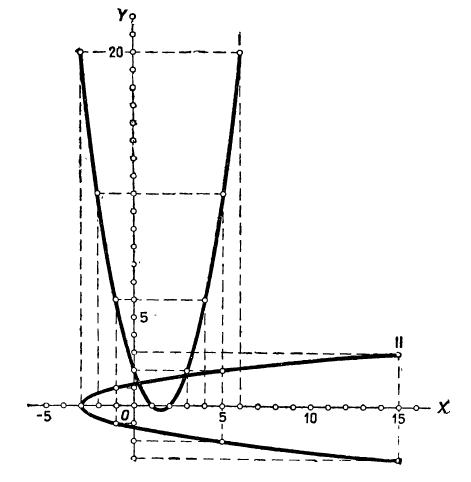
По этим значениям построим графики (эти графики будут параболы, черт. 24).
Графики пересекаются в двух точках, координаты которых приблизительно будут: х=0,3; y=1,3 и x=2,8; y=l,6.
Можно найти координаты точек пересечения точнее, если начертим в более крупном масштабе те части графиков, которые лежат около точек пересечения.
Видео:Всё о квадратичной функции. Парабола | Математика TutorOnlineСкачать

Квадратичная функция — основные понятия и определения
Функция — одно из важнейших математических понятий. Напомним, что функцией называют такую зависимость переменной у от переменной х, при которой каждому значению переменной х соответствует единственное значение переменной у.
Переменную х называют независимой переменной или аргументом. Переменную у называют зависимой переменной. Говорят также, что переменная у является функцией от переменной х. Значения зависимой переменной называют значениями функции.
Если зависимость переменной у от переменной х является функцией, то коротко это записывают так: y = f(x). (Читают: у равно / от х.) Символом / (х) обозначают значение функции, соответствующее значению аргумента, равному х.
Пусть, например, функция задается формулой 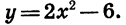
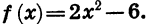
Заметим, что в записи вида y = f(x) вместо f употребляют и другие буквы: 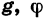
Все значения независимой переменной образуют область onределения функции. Все значения, которые принимает зависимая переменная, образуют область значений функции.
Если функция задана формулой и ее область определения не указана, то считают, что область определения функции состоит из всех значений аргумента, при которых формула имеет смысл. Например, областью определения функции 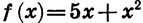
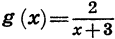
Область определения функции, описывающей реальный процесс, зависит от конкретных условий его протекания. Например, зависимость длины l железного стержня от температуры нагревания t выражается формулой 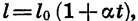
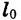
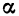
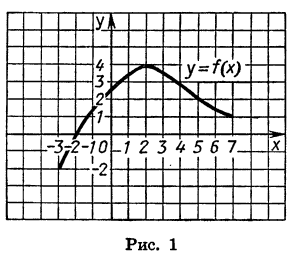
Напомним, что графиком функции называют множество всех точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты — соответствующим значениям функции.
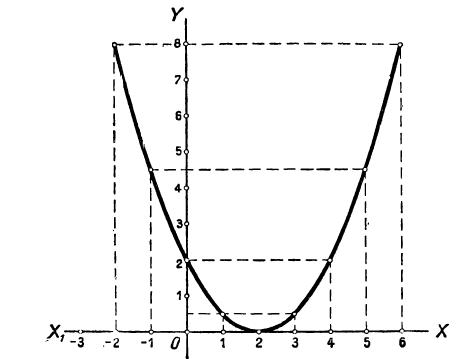
На рисунке 1 изображен график функции y = f(x), областью определения которой является промежуток [ — 3; 7]. С помощью графика можно найти, например, что f(— 3) = — 2, f(0) = 2,5, f(2) = 4, f(5) = 2. Наименьшее значение функции равно —2, а наибольшее равно 4; при этом любое число от —2 до 4 является значением данной функции. Таким образом, областью значений функции y = f(x) служит промежуток [-2; 4].
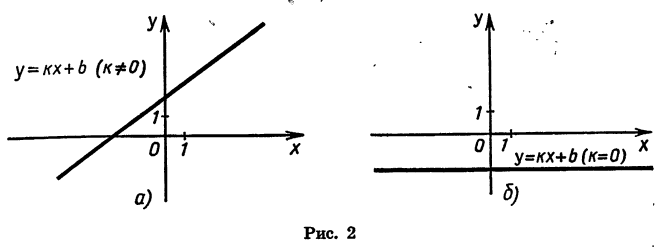
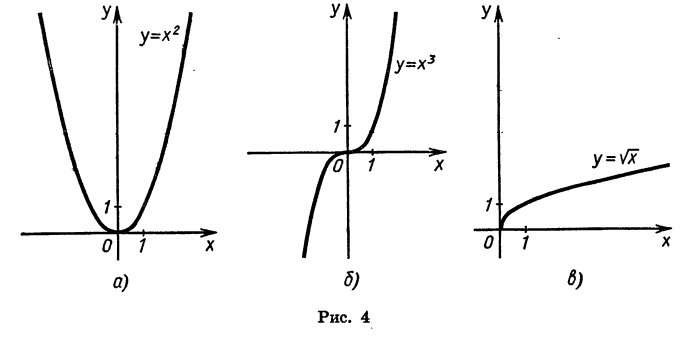
Мы изучили некоторые важные виды функций: линейную функцию, т. е. функцию, задаваемую формулой 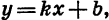
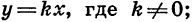
Графиком функции 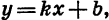
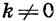
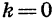
График функции 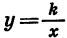
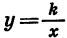

Функциями такого вида описываются многие реальные процессы и закономерности. Например, прямой пропорциональностью является зависимость массы тела m от его объема V при постоянной плотности 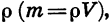
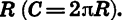
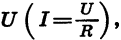
Мы рассматривали также функции, заданные формулами 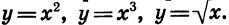
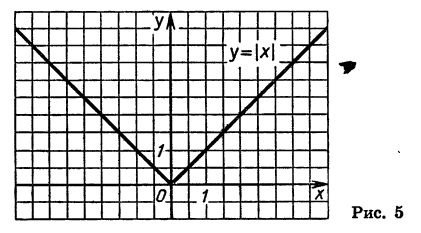
Рассмотрим еще одну функцию, а именно функцию, заданную формулой
Так как выражение |х| имеет смысл при любом х, то областью определения этой функции является множество всех чисел. По определению |х| = х, если 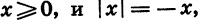
График рассматриваемой функции в промежутке
совпадает с графиком функции у = х, а в промежутке 
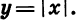
Свойства функции
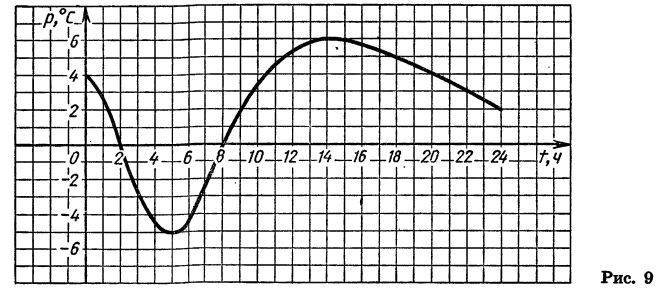
На рисунке 9 изображен график зависимости температуры воздуха р (в °С) от времени суток t (в часах). Мы видим, что в 2 ч и в 8 ч температура равнялась нулю, от 0 до 2 ч и от 8 до 24 ч она была выше нуля, а от 2 до 8 ч — ниже нуля. Из графика ясно также, что в течение первых пяти часов температура понижалась, затем в промежутке от 5 до 14 ч она повышалась, а потом опять понижалась.
С помощью графика мы выяснили некоторые свойства функции p=f(t), где t — время суток в часах, а р — температура воздуха в градусах Цельсия.
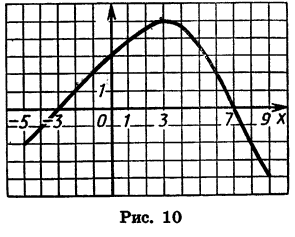
Рассмотрим теперь свойства функции y = f (х), график которой изображен на рисунке 10. Выясним сначала, при каких значениях х функция обращается в нуль, принимает положительные и отрицательные значения.
Найдем абсциссы точек пересечения графика с осью х. Получим х = — 3 и х = 7. Значит, функция принимает значение, равное нулю, при х = — 3 и х = 7. Значения аргумента, при которых функция обращается в нуль, называют нулями функции, т. е. числа -3 и 7 — нули рассматриваемой функции.
Нули функции разбивают ее область определения — промежуток [- 5; 9] на три промежутка: [-5; -3), (-3; 7) и (7; 9]. Для значений х из промежутка (-3; 7) точки графика расположены выше оси х, а для значений х из промежутков [- 5; — 3) и (7; 9] — ниже оси х. Значит, в промежутке ( — 3; 7) функция принимает положительные значения, а в каждом из промежутков [-5; -3) и (7; 9] — отрицательные.
Выясним теперь, как изменяются (увеличиваются или уменьшаются) значения данной функции с изменением х от — 5 до 9.
Из графика видно, что с увеличением х от -5 до 3 значения у увеличиваются, а с увеличением х от 3 до 9 значения у уменьшаются. Говорят, что в промежутке [-5; 3] функция y = f(x) является возрастающей, а в промежутке [3; 9] эта функция является убывающей.
Определение:
Функция называется возрастающей в некотором промежутке, если большему значению аргумента из этого промежутка соответствует большее значение функции;
функция называется убывающей в некотором промежутке, если большему значению аргумента из этого промежутка соответствует меньшее значение функции.
Иными словами, функцию y = f (х) называют возрастающей в некотором промежутке, если для любых 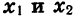

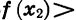
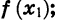
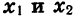

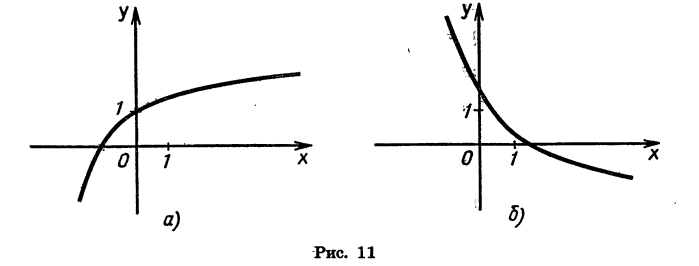
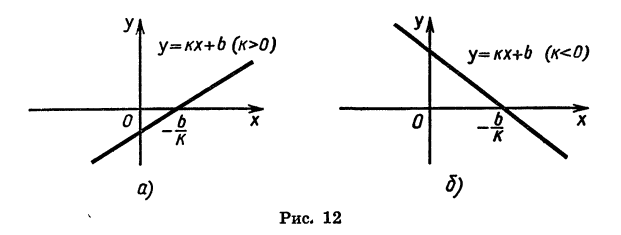
Если функция возрастает на всей области определения, то ее называют возрастающей функцией, а если убывает, то убывающей функцией. На рисунке 11 изображены графики возрастающей функции и убывающей функции.
Выясним, какими свойствами обладают некоторые изученные ранее функции.
Пример 1. Рассмотрим свойства функции 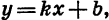
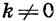
- Решив уравнение
найдем, что
Значит, у=0, при
- Выясним, при каких значениях х функция принимает положительные значения и при каких — отрицательные. Рассмотрим два случая:
Пусть 
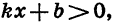
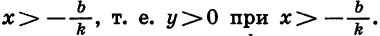
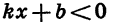
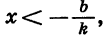
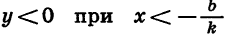
Пусть 
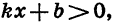
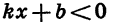
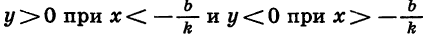
3. При 
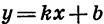

Докажем это. Пусть 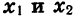

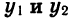
Рассмотрим разность
Множитель 

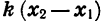
Если 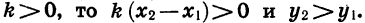

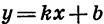
Если 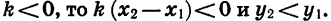
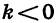
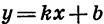
Пример:
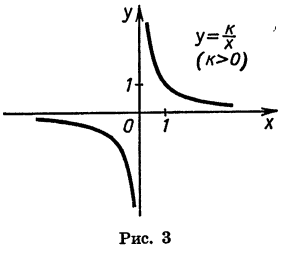
Рассмотрим свойства функции 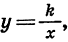
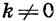
1.Так как дробь 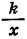
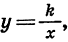
2. Если 
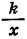
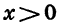
Если 
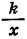
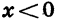
3. При 
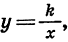
из промежутков 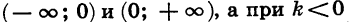
Доказательство этого свойства проводится аналогично тому, как это было сделано для линейной функции.
Заметим, что, хотя функция 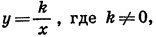
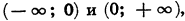
Видео:Как построить график функции без таблицыСкачать

Квадратный трехчлен
Квадратный трехчлен и его корни
Выражение 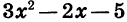
Определение:
Квадратным трехчленом называется многочлен вида 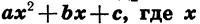
Значение квадратного трехчлена 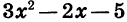
Мы видим, что при х = -1 квадратный трехчлен 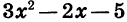
Корнем квадратного трехчлена называется значение переменной, при котором значение этого трехчлена равно нулю.
Для того чтобы найти корни квадратного трехчлена 

Пример:
Найдем корни квадратного трехчлена .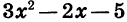
Значит, квадратный трехчлен 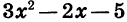
Так как квадратный трехчлен 

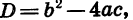
Преобразуем выражение в скобках. Для этого представим 12х в виде произведения 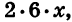
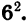
Рассмотрим задачу, при решении которой применяется выделение квадрата двучлена из квадратного трехчлена.
Пример:
Докажем, что из всех прямоугольников с периметром 20 см наибольшую площадь имеет квадрат.
Пусть одна сторона прямоугольника равна х см. Тогда другая сторона равна 10 — х см, а площадь прямоугольника равна
Раскрыв скобки в выражении х (10 — х), получим 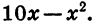
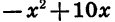
Так как выражение 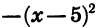
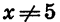
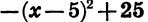
Разложение квадратного трехчлена на множители
Пусть требуется разложить на множители квадратный трехчлен 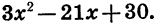
Для того чтобы разложить на множители трехчлен 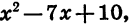
При х = 2 и х = 5 произведение 3 (х — 2) (х — 5), а следовательно, и трехчлен 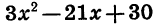
Мы представили квадратный трехчлен 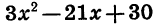
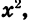
Такое разложение можно получить для любого квадратного трехчлена, имеющего корни. При этом считают, что если дискриминант квадратного трехчлена равен нулю, то этот трехчлен имеет два равных корня.
Теорема:
Если 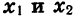

Вынесем за скобки в многочлене 
Так как корни квадратного трехчлена 

Заметим, что если квадратный трехчлен не имеет корней, то его нельзя разложить на множители, являющиеся многочленами первой степени.
Докажем это. Пусть трехчлен 
где 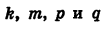
Произведение (kx+m) ( +q) обращается в нуль при
Следовательно, при этих значениях х обращается в нуль и трехчлен

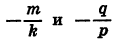
Пример:
Разложим на множители квадратный трехчлен
Решив уравнение 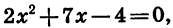
По теореме о разложении квадратного трехчлена на множители имеем:
Полученный результат можно записать иначе, умножив число 2 на двучлен 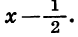
Пример:
Разложим на множители квадратный трехчлен
Решив уравнение 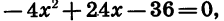
Пример:
Сократим дробь
Разложим на множители квадратный трехчлен 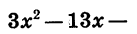
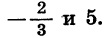
Квадратичная функция и ее график
Функция 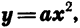
Одной из важных функций, которую мы будем рассматривать в дальнейшем, является квадратичная функция.
Определение:
Квадратичной функцией называется функция, которую можно задать формулой вида у = 
Примером квадратичной функции является зависимость пути от времени при равноускоренном движении. Если тело движется с ускорением 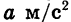
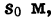
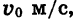
Если, например, а = 6, 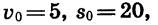
Изучение квадратичной функции мы начнем с частного случая — функции
При а = 1 формула 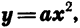
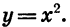
Построим график функции 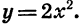
Построим точки, координаты которых указаны в таблице. Соединив их плавной линией, получим график функции 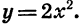
При любом 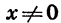
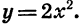


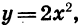

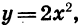

Построим теперь график функции 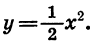
Построив точки, координаты которых указаны в таблице, и соединив их плавной линией, получим график функции 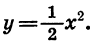
При любом 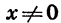
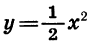


перейдет в точку графика функции 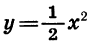

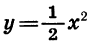

Вообще график функции 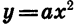

Рассмотрим теперь функцию 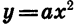
Воспользовавшись этой таблицей, построим график функции 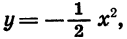
Сравним графики функций 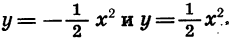
При любом х значения этих функций являются противоположными числами. Значит, соответствующие точки графиков симметричны относительно оси х. Иными словами, график функции
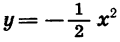
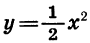
Вообще графики функций 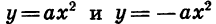
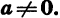
График функции 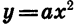
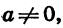

Сформулируем свойства функции 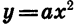
1.Если х = 0, то у = 0. График функции проходит через начало координат.
2. Если 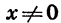
3. Противоположным значениям аргумента соответствуют равные значения функции. График функции симметричен относительно оси у.
4. Функция убывает в промежутке 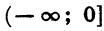
5. Наименьшее значение, равное нулю, функция принимает при х = 0, наибольшего значения функция не имеет. Областью значений функции является промежуток
Докажем свойство 4. Пусть 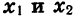
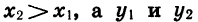
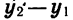
Так как 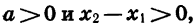
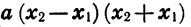
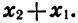
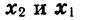
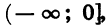
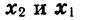
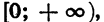
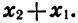
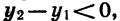

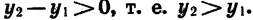
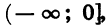
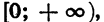
Теперь сформулируем свойства функции 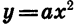
Из перечисленных свойств следует, что при а > 0 ветви параболы 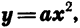
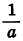
График функции 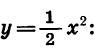
Чтобы получить таблицу значений функции 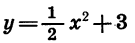
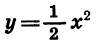
Построим точки, координаты которых указаны в таблице (2), и соединим их плавной линией. Получим график функции 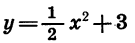
Легко понять, что каждой точке 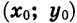
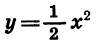
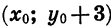
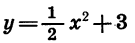
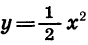
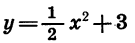
График функции 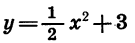
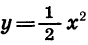
Вообще график функции 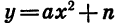
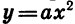
Пример:
Рассмотрим теперь функцию 
Для этого в одной системе координат построим графики функций
Для построения графика функции 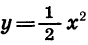


Построим график функции 
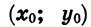
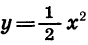
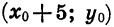

Значит, если переместить каждую точку графика функции 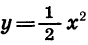

График функции 
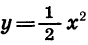
Вообще график функции 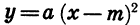
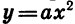
Вообще график функции 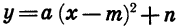
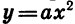
Рассмотрим квадратичную функцию у = 

Мы получили формулу вида 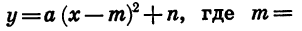
Значит, график функции 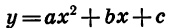
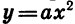
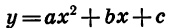
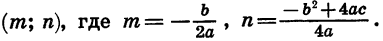
Приведем примеры построения графиков квадратичных функций.
Пример:
Построим график функции 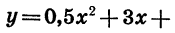
Графиком функции 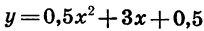
Значит, вершиной параболы является точка ( — 3; —4). Составим таблицу значений функции:
Построив точки, координаты которых указаны в таблице, и соединив их плавной линией, получим график функции 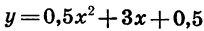
При составлении таблицы и построении графика учитывалось, что прямая х = — 3 является осью симметрии параболы. Поэтому мы брали точки с абсциссами — 4 и — 2, — 5 и — 1, — 6 и 0, симметричные относительно прямой х = — 3 (эти точки имеют одинаковые ординаты).
Пример:
Построим график функции 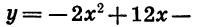
Графиком этой функции является парабола, ветви которой направлены вниз. Найдем координаты ее вершины:
Вычислив координаты еще нескольких точек, получим таблицу:
Соединив плавной линией точки, координаты которых указаны в таблице, получим график функции 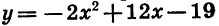
Пример:
Построим график функции
Графиком функции 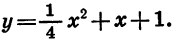
Вычислив координаты еще нескольких точек, получим таблицу:
График функции 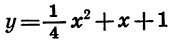
Видео:Квадратичная функция за 5 минутСкачать

Решение неравенств второй степени с одной переменной
Неравенства вида 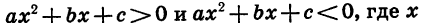
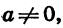
Решение неравенства второй степени с одной переменной можно рассматривать как нахождение промежутков, в которых соответствующая квадратичная функция принимает положительные или отрицательные значения.
Пример:
Решим неравенство
Рассмотрим функцию 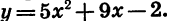
Выясним, как расположена эта парабола относительно оси х. Для этого решим уравнение
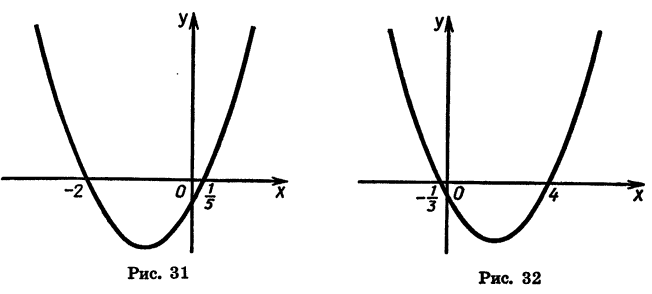
Значит, парабола пересекает ось х в двух точках, абсциссы которых равны
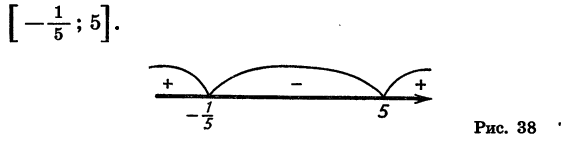
Покажем схематически, как расположена парабола в координатной плоскости (рис. 31). Из рисунка видно, что функция принимает отрицательные значения, когда
Следовательно, множеством решений неравенства 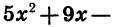
Покажем схематически, как расположена парабола в координатной плоскости (рис. 32). Из рисунка видно, что данное неравенство верно, если х принадлежит промежутку 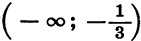
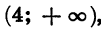
является объединение промежутков
Ответ можно записать так:
Пример:
Решим неравенство
Рассмотрим функцию 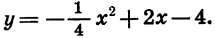
Выясним, как расположен график относительно оси х. Решим для этого уравнение 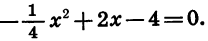
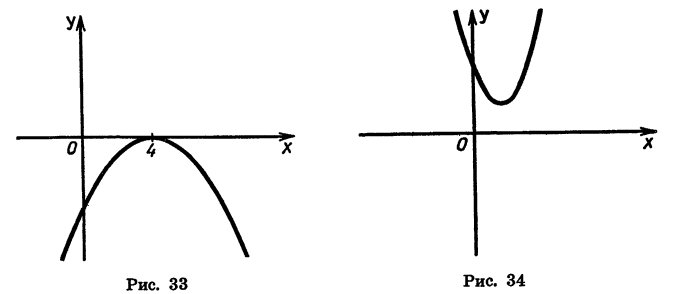
Изобразив схематически параболу (рис. 33), найдем, что функция принимает отрицательные значения при любом х, кроме 4.
Ответ можно записать так: х — любое число, не равное 4.
Пример:
Решим неравенство
График функции 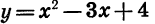
Чтобы выяснить, как расположена парабола относительно оси х, решим уравнение 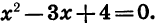
2) если трехчлен имеет корни, то отмечают их на оси х и через отмеченные точки проводят схематически параболу, ветви которой направлены вверх при а > 0 или вниз при а 0 или в нижней при а Решение неравенств методом интервалов
Областью определения этой функции является множество всех чисел. Нулями функции служат числа — 2, 3, 5. Они разбивают область определения функции на промежутки
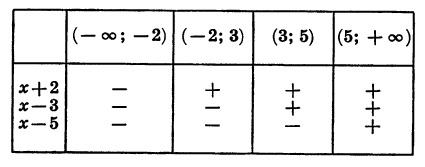
Выражение (х + 2) (х — 3) (х — 5) представляет собой произведение трех множителей. Знак каждого из этих множителей в рассматриваемых промежутках указан в таблице:
Отсюда ясно, что:
Мы видим, что в каждом из промежутков 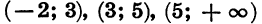
где х — переменная, а 

Это свойство используется для решения неравенств вида
где 
Пример:
Данное неравенство является неравенством вида (1), так как в левой части записано произведение 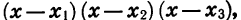
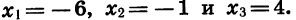
Отметим на координатной прямой нули функции
Найдем знаки этой функции в каждом из промежутков 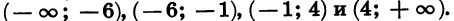
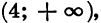
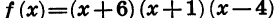
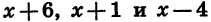
Из рисунка видно, что множеством решений неравенства является объединение промежутков
Ответ:
Рассмотренный способ решения неравенств называют методом интервалов.
Рассмотрим теперь примеры решения неравенств, которые сводятся к неравенствам вида (1).
Пример:
Решим неравенство
Приведем данное неравенство к виду (1). Для этого в двучлене 0,5 — х вынесем за скобку множитель -1. Получим:
Мы получили неравенство вида (1), равносильное данному.
Отметим на координатной прямой нули функции f (х) = х (х — 0,5)(х + 4) (рис. 37, а). Покажем знаком «плюс», что в крайнем справа промежутке функция принимает положительное значение, а затем, двигаясь справа налево, укажем знак функции в каждом из промежутков (рис. 37, б). Получим, что множеством решений неравенства является объединение промежутков
Ответ:
Пример:
Решим неравенство
Приведем неравенство к виду (1). Для этого в первом двучлене вынесем за скобки множитель 5, а во втором —1, получим:
Разделив обе части неравенства на -5, будем иметь:
Отметим на координатной прямой нули функции f(x) 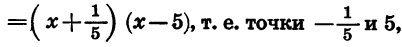
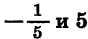
Ответ:
Заметим, что данное неравенство можно решить иначе, воспользовавшись свойствами графика квадратичной функции.
Пример:
Решим неравенство
Так как знак дроби 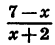
Приведя неравенство 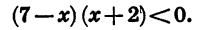
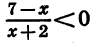
Ответ:
Видео:Как легко составить уравнение параболы из графикаСкачать

Квадратичная функция и её построение
Парабола
Если х и у рассматривать как координаты точки, то уравнение (1) определит некоторое геометрическое место точек. Исследуем вид этого геометрического места. Заметим, что наше исследование будет неполным, так как останутся вопросы, которые нами пока не будут выяснены. Чем дальше мы будем продвигаться в изучении математики, тем полнее будут проводиться исследования.
1) Так как 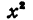
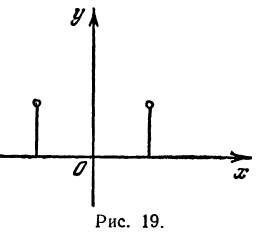
2) Так как и для —х и для х после возведения в квадрат получается одно и то же число, то точки, принадлежащие геометрическому месту и соответствующие значениям — х и х, имеют одну и ту же ординату и поэтому расположены симметрично относительно оси Оу (рис. 19).
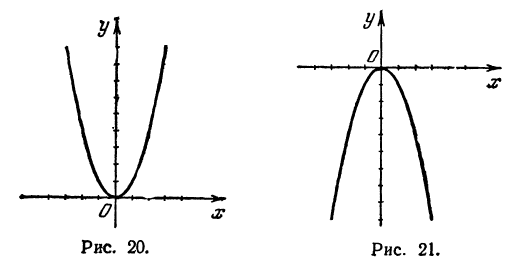
3) Если х положительно, то, чем больше х, тем больше и 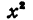
Геометрическое место, определяемое уравнением 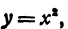
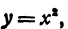
Теперь рассмотрим уравнение
Оно определяет геометрическое место точек. Сравнивая уравнения (1) и (2), замечаем, что при одном и том же х значения у отличаются только знаками, именно у, полученный из уравнения (2), всегда неположителен. Поэтому уравнение (2) тоже определяет параболу, вершина которой также находится в точке (0, 0), но ветви этой которой также находится в точке (0, 0), но ветви этой параболы идут от начала координат вниз вправо и вниз влево. График функции (2) изображен на рис. 21
Перейдем к рассмотрению уравнения
Сравним его с уравнением (1),
Если а положительно и больше единицы, то очевидно, что при одном и том же значении х величина у из уравнения (3) будет больше, чем величина у, взятая из уравнения (1). Отсюда можно заключить, что кривая, определяемая уравнением (3), отличается от параболы (1) только тем, что ординаты ее точек растянуты в а раз. Таким образом, кривая, определяемая уравнением (3), является более сжатой, чем парабола 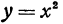
Если 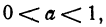
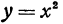
Теперь покажем, что кривая, определяемая уравнением
является параболой, только ее расположение относительно координатных осей другое, чем в разобранных случаях. Предварительно рассмотрим параллельный перенос осей координат.
Параллельный перенос осей координат
Пусть на плоскости дана система координат хОу (рис. 23). Рассмотрим новую систему координат 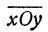
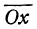
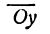
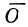
Обозначим координаты нового начала 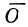
Возьмем произвольную точку М на плоскости; пусть ее координаты в старой системе будут х и у, а в новой 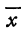
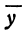
и (на основании формулы (2) из § 1 гл. I)
Переход от старой системы координат к указанной новой называется параллельным переносом или параллельным сдвигом осей координат. Приходим к выводу:
При параллельном сдвиге осей координат старая координата точки равна новой координате той же точки плюс координата нового начала в старой системе.
Исследование функции
Функция, определенная уравнением
называется квадратичной функцией. Функция 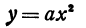
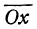
а ось 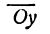
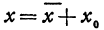
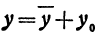
Разрешив это уравнение относительно 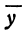
Координаты нового начала находятся в нашем распоряжении, поэтому их можно выбрать так, чтобы выполнялись условия
В этих уравнениях два неизвестных: х0 и у0. Найдем их:
Если взять новое начало в точке
то в уравнении (2) скобки
сделаются равными нулю, т. е. уравнение (2) примет вид
Полученное уравнение имеет вид, рассмотренный выше. Таким образом, уравнение 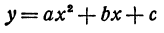
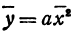
Уравнение 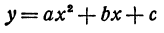
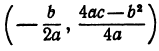
Переносим начало координат в точку (х0, у0), координаты которой пока неизвестны. Старые координаты я, у выражаются через новые 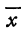
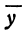
Подставляя эти выражения в уравнение (4), получим:
Выберем координаты нового начала так, чтобы соблюдались равенства
Решая полученную систему уравнений, будем иметь:
Следовательно, перенося начало координат в точку 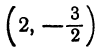
Следовательно, уравнение (4) определяет параболу, имеющу вершину в точке 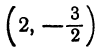
Приведем пример применения квадратичной функции в механике.
Задача:
Найти траекторию тела, брошенного под углом к горизонту. Угол бросания а, скорость бросания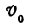
Решение:
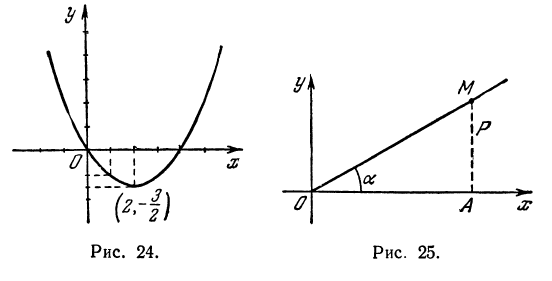
Выберем оси координат так: ось Оу—вертикальная прямая, проведенная в точке бросания , ось Ох— горизонтальная прямая, начало координат—точка бросания (рис. 25).
Если бы не действовала сила притяжения Земли, то тело, брошенное под углом к горизонту, по инерции двигалось бы по прямой ОМ. За t сек оно прошло бы расстояние 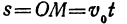
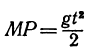
Найдем уравнение, связывающее х с у. Для этого из уравнения (*) найдем t и подставим это выражение в уравнение (**):
Мы получили уравнение траектории тела. Как мы видим, это есть квадратичная функция рассмотренного вида, следовательно, тело, брошенное под углом к горизонту, движется в безвоздушном пространстве по параболе, расположенной вершиной вверх, поскольку коэффициент при 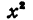
Какова наибольшая высота подъема тела над Землей? Чтобы ответить на этот вопрос, нужно найти вершину параболы. Как было выведено, вершина параболы имеет координаты
этому координаты вершины равны
Найдем теперь дальность полета тела, т. е. абсциссу точки падения. Для этого приравняем в уравнении (***) у нулю, получим уравнение
решая которое найдем два значения
первое из них дает точку бросания, а второе — искомую абсциссу точки падения.
Все эти рассуждения относятся к безвоздушному пространству; в воздухе и высота и дальность будут значительно меньше.
Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
💡 Видео
Неполные квадратные уравнения. Алгебра, 8 классСкачать

Функция у=х² и у=х³ и их графики. Алгебра, 7 классСкачать

7 класс, 35 урок, Графическое решение уравненийСкачать

Задание 23 из ОГЭ Построение графиков функций с модулем | МатематикаСкачать

Построение графика квадратичной функции. Алгебра, 9 классСкачать

Как запомнить графики функцийСкачать

Решение квадратных неравенств | МатематикаСкачать

Уравнение с двумя переменными и его график. Алгебра, 9 классСкачать

решаем квадратные уравнения в ExcelСкачать
















































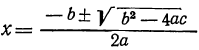
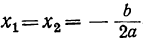
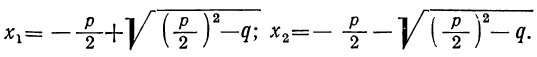
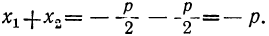
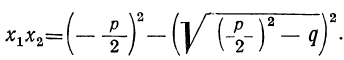
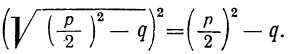
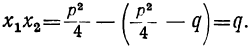
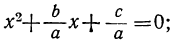
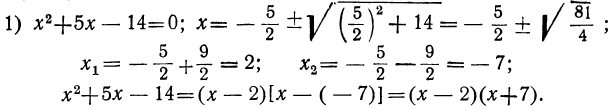
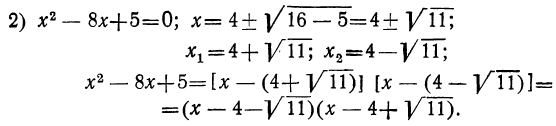
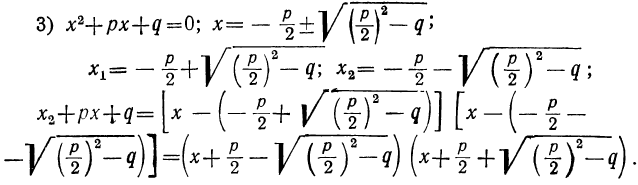
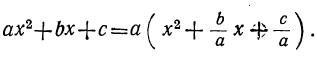
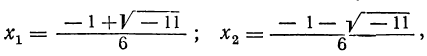
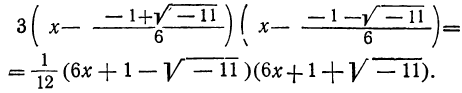
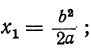
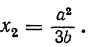
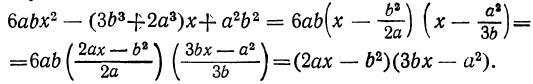
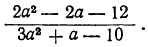
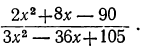
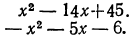
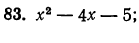
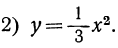
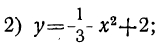
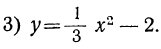
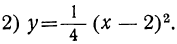
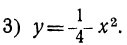
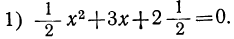
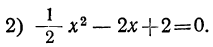
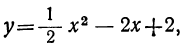
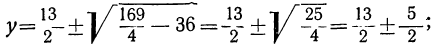
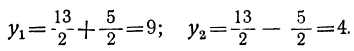
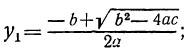
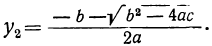
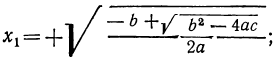
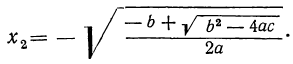
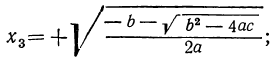
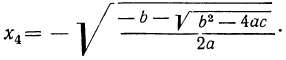
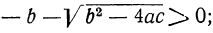
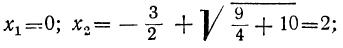
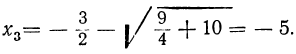
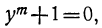
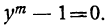
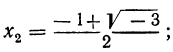
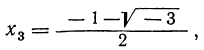
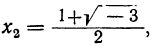
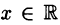
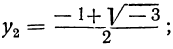
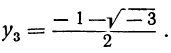
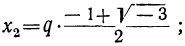
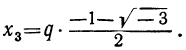
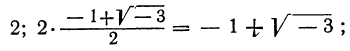
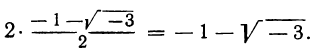
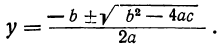
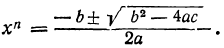
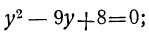
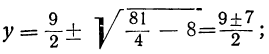
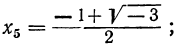
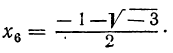
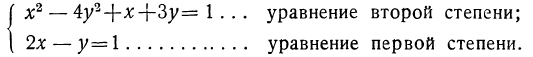
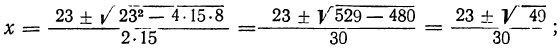
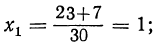
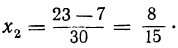
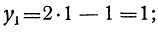
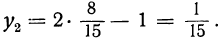
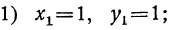
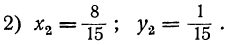
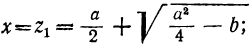
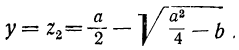
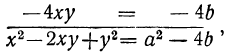
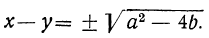
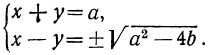
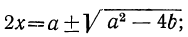
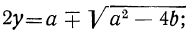
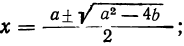
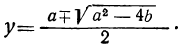
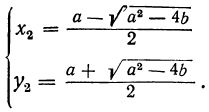
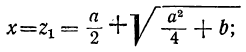
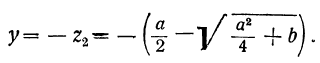
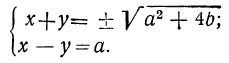
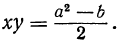
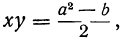
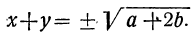
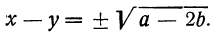
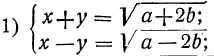
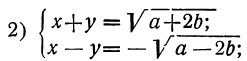
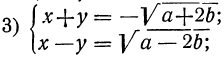
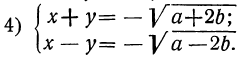
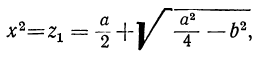
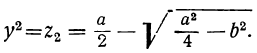
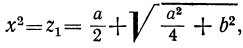
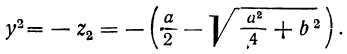
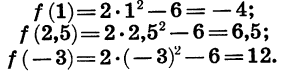
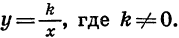
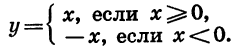
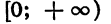

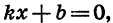 найдем, что
найдем, что 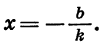 Значит, у=0, при
Значит, у=0, при