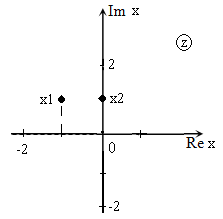Решение квадратного уравнения по формуле муавра

Видео:Формула Муавра. Возведение комплексного числа в степеньСкачать

Формула Муавра

Содержание:

Задание комплексных чисел в тригонометрической форме удобно при выполнении над числами действий умножения, деления, возведения в степень и извлечения корня.

Найдем произведение двух комплексных чисел, записанных в тригонометрической форме; пусть

Выражения, стоящие в круглых скобках, можно упростть с помощью известных формул (115.4), (116.1):

По этой ссылке вы найдёте полный курс лекций по высшей математике:

Доказано правило: для умножения чисел, заданных в тригонометрической форме у их модули надо перемножить, а аргументы сложить.

Это правило остается верным для любого количества сомножителей.

Примеры с решением

Пример 1.

Найти произведение чисел

Решение:

Так как деление—действие, обратное умножению, то легко вывести следующее правило: для выполнения деления двух комплексных чисел, заданных в тригонометрической форме, следует их модули разделитьу а аргументы вычесть:

Возможно вам будут полезны данные страницы:

Пример 2.

Найти частное от деления числа на число

Решение:

Находим по формуле (17.2):

Используем теперь равенство (17,1) для возведения произвольного комплексного числа в натуральную степень Для этого придется модуль этого числа взять множителем раз и аргумент взять слагаемым раз. Это приводит к равенству

Равенство (17.3) называется формулой Муавра. Из нее следует, что для возведения комплексного числа в любую натуральную степень его модуль нужно возвести в эту степень у а аргумент умножить на показатель степени.

Пример 3.

Вычислить

Решение:

В соответствии с формулой Муавра (17.3)

Если число задано в алгебраической форме то для возведения его в степень с помощью формулы Муавра надо предварительно записать его в тригонометрической форме.

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.

Видео:Формула Муавра ➜ Вычислить ➜ (5+5i)⁷Скачать

Тригонометрическая форма комплексных чисел

Второй урок по комплексным числам. Если вы только начинаете изучать эту тему (что такое комплексная единица, модуль, сопряжённые), см. первый урок: «Что такое комплексное число».

Сегодня мы узнаем:

Начнём с ключевого определения.

Видео:Комплексные корни квадратного уравненияСкачать

1. Тригонометрическая форма

Определение. Тригонометрическая форма комплексного числа — это выражение вида

[z=left| z right|cdot left( cos text!!varphi!!text+isin text!!varphi!!text right)]

где $left| z right|$ — модуль комплексного числа, $text!!varphi!!text$ — некоторый угол, который называется аргумент комплексного числа (пишут $text!!varphi!!text=arg left( z right)$).

Любое число $z=a+bi$, отличное от нуля, можно записать с тригонометрической форме. Для этого нужно вычислить модуль и аргумент. Например:

Записать в тригонометрической форме число $z=sqrt+i$.

Переписываем исходное число в виде $z=sqrt+1cdot i$ и считаем модуль:

Выносим модуль за скобки:

[z=sqrt+1cdot i=2cdot left( frac<sqrt>+fraccdot i right)]

Вспоминаем тригонометрию, 10-й класс:

Понятно, что вместо $frac<text!!pi!!text>$ с тем же успехом можно взять аргумент $frac<13text!!pi!!text>$. Синус и косинус не поменяется. Главное — выбрать такой аргумент, чтобы в тригонометрической форме не осталось никаких минусов. Все минусы должны уйти внутрь синуса и косинуса. Сравните:

Записать в тригонометрической форме число $z=-1-i$.

Видео:Комплексные числа. Тригонометрическая форма. Формула Муавра | Ботай со мной #040 | Борис Трушин !Скачать

2. Умножение и деление комплексных чисел

Комплексные числа, записанные в тригонометрической форме, очень удобно умножать и делить.

Теорема. Пусть даны два комплексных числа:

[begin & <_>=left| <_> right|cdot left( cos alpha +isin alpha right) \ & <_>=left| <_> right|cdot left( cos beta +isin beta right) \ end]

Тогда их произведение равно

[<_>cdot <_>=left| <_> right|cdot left| <_> right|cdot left( cos left( alpha +beta right)+isin left( alpha +beta right) right)]

А если ещё и $left| <_> right|ne 0$, то их частное равно

Получается, что при умножении комплексных чисел мы просто умножаем их модули, а аргументы складываем. При делении — делим модули и вычитаем аргументы. И всё!

Найти произведение и частное двух комплексных чисел:

[begin <_>cdot <_> & =2cdot 5cdot left( cos left( frac+frac right)+isin left( frac+frac right) right)= \ & =10cdot left( cos frac+isin frac right) \ end]

[begin frac<<_>><<_>> & =fraccdot left( cos left( frac-frac right)+isin left( frac-frac right) right)= \ & =0,4cdot left( cos frac+isin frac right) \ end]

По сравнению со стандартной (алгебраической) формой записи комплексных чисел экономия сил и времени налицо.:)

Видео:Комплексные корни квадратных уравнений. 11 класс.Скачать

3. Формула Муавра

Пусть дано комплексное число в тригонометрической форме:

[z=left| z right|cdot left( cos text!!varphi!!text+isin text!!varphi!!text right)]

Возведём его в квадрат, умножив на само себя:

[begin <^> & =zcdot z = \ & =left| z right|left| z right|cdot left( cos left( text!!varphi!!text!!varphi!!text right)+isin left( text!!varphi!!text!!varphi!!text right) right)= \ & =<^>cdot left( cos 2text!!varphi!!text+isin 2text!!varphi!!text right) \ end]

Затем возведём в куб, умножив на себя ещё раз:

Несложно догадаться, что будет дальше — при возведении в степень $n$. Это называется формула Муавра.

Формула Муавра. При возведении всякого комплексного числа

[z=left| z right|cdot left( cos varphi +isin varphi right)]

в степень $nin mathbb$ получим

Простая формула, которая ускоряет вычисления раз в десять! И кстати: эта формула работает при любом $nin mathbb$, а не только натуральном. Но об этом позже. Сейчас примеры:

Представим первое число в тригонометрической форме:

[begin sqrt-i & = 2cdot left( frac<sqrt>+icdot left( -frac right) right)= \ & =2cdot left( cos left( -frac right)+isin left( -frac right) right) \ end]

По формуле Муавра:

Последним шагом мы воспользовались периодичностью синуса и косинуса, уменьшив аргумент сразу на 28π.

Следующую задачу в разных вариациях любят давать на контрольных работах и экзаменах:

Теперь второе число запишем в комплексной форме:

По формуле Муавра:

Вот так всё просто! Следующие два раздела предназначены для углублённого изучения. Для тех, кто хочет действительно разобраться в комплексных числах.

Видео:Формула корней квадратного уравнения. Алгебра, 8 классСкачать

4. Дополнение 1. Геометрический подход

Многие путают местами косинус и синус. Почему комплексная единица стоит именно у синуса? Вспомним, что есть декартова система координат, где точки задаются отступами по осям $x$ и $y$:

А есть полярная система координат, где точки задаются поворотом на угол $varphi $ и расстоянием до центра $r$:

А теперь объединим эти картинки и попробуем перейти из декартовой системы координат в полярную:

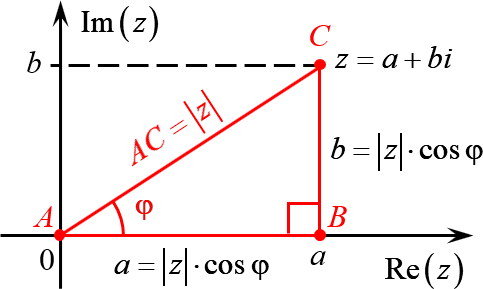
Комплексное число $z=a+bi$ задаёт на плоскости точку $C$, удалённую от начала координат на расстояние

Треугольник $ABC$ — прямоугольный. Пусть $angle BAC=varphi $. Тогда:

[begin & AB=ACcdot cos varphi =left| z right|cdot cos varphi \ & BC=ACcdot sin varphi =left| z right|cdot sin varphi \ end]

С другой стороны, длины катетов $AB$ и $BC$ — это те самые отступы $a$ и $b$, с помощью которых мы задаём комплексное число. Поэтому:

[begin a+bi & =left| z right|cos varphi +icdot left| z right|sin varphi = \ & =left| z right|left( cos varphi +isin varphi right) \ end]

Итак, мы перешли от пары $left( a;b right)$ к паре $left( left| z right|;varphi right)$, где $left| z right|$ — модуль комплексного числа, $varphi $ — его аргумент (проще говоря, угол поворота).

Важное замечание. А кто сказал, что такой угол $varphi $ существует? Возьмём число $z=a+bi$ и вынесем модуль за скобку:

Осталось подобрать такой угол $varphi $, чтобы выполнялось два равенства:

Такой угол обязательно найдётся, поскольку выполняется основное тригонометрическое тождество:

На практике основная трудность заключается именно в поиске подходящего аргумента.

Видео:Решение квадратных уравнений. Дискриминант. 8 класс.Скачать

5. Дополнение 2. Как найти аргумент?

В учебниках пишут много разной дичи, типа вот этой:

Формула правильная, но пользы от неё — ноль. Запомнить сложно, а применять и вовсе невозможно. Мы пойдём другим путём.

5.1. Точки на координатных осях

Для начала рассмотрим точки, лежащие осях координат.

Тут всё очевидно:

• На положительной полуоси абсцисс $varphi =0$ (фиолетовая точка $A$).
• На отрицательной — $varphi =pi $ (синяя точка $B$).
• На положительной полуоси ординат $varphi =frac$ (зелёная точка $B$).
• На отрицательной — $varphi =frac$ (красная точка $C$). Однако ничто не мешает рассмотреть $varphi =-frac$ — результат будет тем же самым.:)

5.2. Точки с арктангенсом

А если точки не лежат на осях, то в записи комплексного числа $a+bi$ числа $ane 0$ и $bne 0$. Рассмотрим вспомогательный угол

Очевидно, это острый угол:

Зная знаки чисел $a$ и $b$, мы немедленно определим координатную четверть, в которой располагается искомая точка. И нам останется лишь отложить вспомогательный угол $<_>$ от горизонтальной оси в эту четверть.

В правой полуплоскости мы откладываем от «нулевого» луча:

Точка $Aleft( 3;4 right)$ удалена от начала координат на расстояние 5:

[begin 3+4i & =5cdot left( cos varphi +isin varphi right) \ varphi & =operatornamefrac end]

Для точки $Bleft( 6;-6 right)$ арктангенс оказался табличным:

[6-6i=6sqrtcdot left( cos left( -frac right)+isin left( -frac right) right)]

В левой полуплоскости откладываем от луча, соответствующего углу $pi $:

Итого для точки $Cleft( -2;5 right)$ имеем:

[begin -2+5i & =sqrtcdot left( cos varphi +isin varphi right) \ varphi & =pi -operatornamefrac end]

И, наконец, для точки $Dleft( -5;-3 right)$:

[begin -5-3i & =sqrtcdot left( cos varphi +isin varphi right) \ varphi & =pi +operatornamefrac end]

Звучит просто, выглядит красиво, работает идеально! Но требует небольшой практики. Пробуйте, тренируйтесь и берите на вооружение.

А в следующем уроке мы научимся извлекать корни из комплексных чисел.:)

Видео:5 способов решения квадратного уравнения ➜ Как решать квадратные уравнения?Скачать

Квадратное уравнение с комплексными корнями

Вы будете перенаправлены на Автор24

Рассмотрим решение уравнений с комплексными корнями и коэффициентами.

Двучленным называется уравнение вида $x^ =A$.

Рассмотрим три случая:

Решить уравнение: $x^ =8$.

Так как $A>0$, то $x_ =sqrt[] cdot left(cos frac +icdot sin frac right),, , , k=0. 2$.

При $k=0$ получаем $x_ =sqrt[] cdot left(cos 0+icdot sin 0right)=sqrt[] =2$.

При $k=1$ получаем

[x_ =sqrt[] cdot left(cos frac +icdot sin frac right)=sqrt[] cdot (-frac +frac <sqrt> cdot i)=2cdot (-frac +frac <sqrt> cdot i)=-1+sqrt cdot i.]

При $k=2$ получаем

[x_ =sqrt[] cdot left(cos frac +icdot sin frac right)=sqrt[] cdot (-frac -frac <sqrt> cdot i)=2cdot (-frac -frac <sqrt> cdot i)=-1-sqrt cdot i.]

Решить уравнение: $x^ =1+i$.

Готовые работы на аналогичную тему

Так как $A$ — комплексное число, то

Тригонометрическая форма записи некоторого комплексного числа имеет вид $z=r(cos varphi +icdot sin varphi )$.

По условию $a=1,b=1$.

Вычислим модуль исходного комплексного числа:

Вычислим аргумент исходного комплексного числа:

[varphi =arg z=arctgfrac =arctg1=frac ]

Подставим полученные значения и получим:

Уравнение перепишем в виде:

При $k=0$ получаем $x_ =sqrt[] <sqrt> cdot left(cos frac +icdot sin frac right)=sqrt[] <sqrt> cdot left(cos frac +icdot sin frac right)=sqrt[] cdot left(cos frac +icdot sin frac right)$.

При $k=1$ получаем

При $k=2$ получаем

Квадратным называется уравнение вида $ax^ +bx+c=0$, где коэффициенты $a,b,c$ в общем случае являются некоторыми комплексными числами.

Решение квадратного уравнения находится с помощью дискриминанта $D=b^ -4ac$, при этом

В случае, когда дискриминант является отрицательным числом, корни данного уравнения являются комплексными числами.

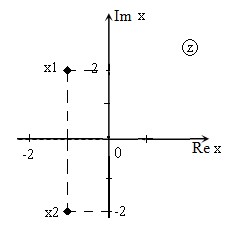
Решить уравнение $x^ +2x+5=0$ и изобразить корни на плоскости.

[D=2^ -4cdot 1cdot 5=4-20=-16.]

Изображение корней уравнения на комплексной плоскости (так как корни комплексные) приведено на рис. 1.

В случае, когда уравнение имеет комплексные корни, они являются комплексно-сопряженными числами.

Комплексное число вида $overline=a-bi$ называется числом комплексно-сопряженным для $z=a+bi$.

Известно, что если $x_ $ являются корнями квадратного уравнения $ax^ +bx+c=0$, то данное уравнение можно переписать в виде $(x-x_ )(x-x_ )=0$. В общем случае $x_ $ являются комплексными корнями.

Зная корни уравнения $x_ =1pm 2i$, записать исходное уравнение.

Запишем уравнение следующим образом:

[x^ -(1-2i)cdot x-xcdot (1+2i)+(1-2i)cdot (1+2i)=0] [x^ -x+2icdot x-x-2icdot x+1-4i^ =0] [x^ -2x+1+4=0] [x^ -2x+5=0]

Следовательно, $x^ -2x+5=0$ — искомое уравнение.

Рассмотрим квадратное уравнение с комплексными коэффициентами.

Решить уравнение: $z^ +(1-2i)cdot z-(1+i)=0$ и изобразить корни на плоскости.

Так как $D>0$, уравнение имеет два корня:

Изображение корней уравнения на комплексной плоскости (так как корни комплексные) приведено на рис. 2.

В случае, когда уравнение имеет комплексные коэффициенты, его корни не обязательно являются комплексно-сопряженными числами.

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 13 11 2021

Сергей Евгеньевич Грамотинский

Эксперт по предмету «Математика»

Работаем по будням с 10:00 до 20:00 по Мск

. и многие другие.
Успешной учебы! Будем рады вам помочь!

🎥 Видео

10 класс, 35 урок, Комплексные числа и квадратные уравненияСкачать

Математика без Ху!ни. Комплексные числа, часть 3. Формы записи. Возведение в степень.Скачать

Математика без Ху!ни. Комплексные числа, часть 4. Извлечение корня n-й степени.Скачать

Решение квадратного уравнения с выводом формулы корнейСкачать

Квадратные уравнения от «А» до «Я». Классификация, решение и теорема Виета | МатематикаСкачать

Комплексные числа в уравненияхСкачать

Возведение в степень и извлечение корня из комплексного числаСкачать

Тригонометрическая форма комплексного числаСкачать

Решение квадратных уравнений в поле комплексных чиселСкачать

КОМПЛЕКСНЫЕ ЧИСЛА ДЛЯ ЧАЙНИКОВ ЗА 7 МИНУТСкачать

Квадратный Трехчлен / Разложение квадратного трехчлена на множители, Как решать Квадратные УравненияСкачать

Формула для корней и теорема Виета | Квадратный трёхчлен #1 | Ботай со мной #020 | Борис ТрушинСкачать