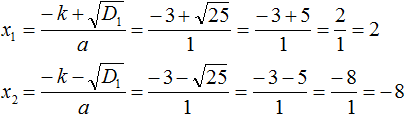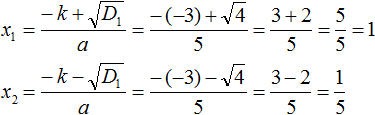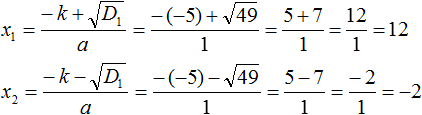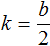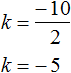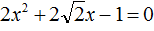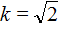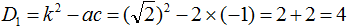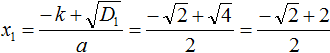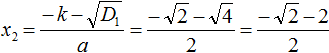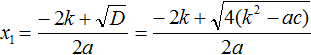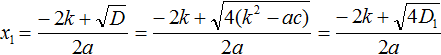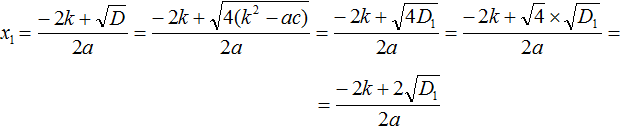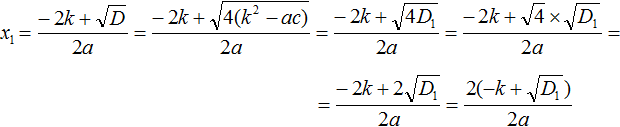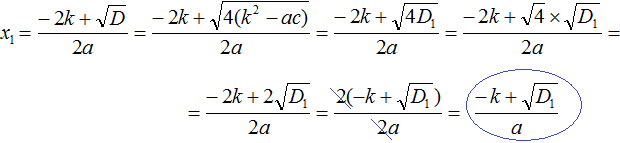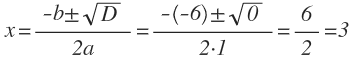Решение квадратного уравнения через половинный дискриминант

Видео:Решение квадратных уравнений. Дискриминант. 8 класс.Скачать

Квадратное уравнение с чётным вторым коэффициентом

Если в квадратном уравнении ax 2 + bx + c = 0 второй коэффициент b является чётным, то решение этого уравнения можно немного упростить. Дискриминант для такого уравнения можно вычислить по формуле D₁ = k 2 − ac , а корни по формулам и .

Видео:Метод переброски в квадратных уравнениях. ЕГЭ и ОГЭ 2022 по математикеСкачать

Примеры

Решим квадратное уравнение x 2 + 6x − 16 = 0 . В нём второй коэффициент является чётным. Чтобы воспользоваться формулами для чётного коэффициента, нужно сначала узнать чему равна переменная k .

Любое четное число n можно представить в виде произведения числа 2 и числа k , то есть 2k .

Например, число 10 можно представить как 2 × 5 .

В этом произведении k = 5 .

Число 12 можно представить как 2 × 6 .

В этом произведении k = 6 .

Число −14 можно представить как 2 × (−7)

В этом произведении k = −7 .

Как видим, сомножитель 2 не меняется. Меняется только сомножитель k .

В уравнении x 2 + 6x − 16 = 0 вторым коэффициентом является число 6 . Это число можно представить как 2 × 3 . В этом произведении k = 3 . Теперь можно воспользоваться формулами для чётного коэффициента.

Найдем дискриминант по формуле D₁ = k 2 − ac

Теперь вычислим корни по формулам: и .

Значит корнями уравнения x 2 + 6x − 16 = 0 являются числа 2 и −8 .

В отличие от стандартной формулы для вычисления дискриминанта ( D=b 2 − 4ac ), в формуле D₁ = k 2 − ac не нужно выполнять умножение числа 4 на ac .

И в отличие от формул и формулы и не содержат в знаменателе множитель 2 что опять же освобождает нас от дополнительных вычислений.

Пример 2. Решить квадратное уравнение 5x 2 − 6x + 1=0

Второй коэффициент является чётным числом. Его можно представить в виде 2 × (−3) . То есть k = −3 . Найдём дискриминант по формуле D₁ = k 2 − ac

Дискриминант больше нуля. Значит уравнение имеет два корня. Для их вычисления воспользуемся формулами и

Пример 3. Решить квадратное уравнение x 2 − 10x − 24 = 0

Второй коэффициент является чётным числом. Его можно представить в виде 2 × (−5) . То есть k = −5 . Найдём дискриминант по формуле D₁ = k 2 − ac

Дискриминант больше нуля. Значит уравнение имеет два корня. Для их вычисления воспользуемся формулами и

Обычно для определения числа k поступают так: делят второй коэффициент на 2.

Действительно, если второй коэффициент b является чётным числом, то его можно представить как b = 2 k . Чтобы из этого равенства выразить сомножитель k , нужно произведение b разделить на сомножитель 2

Например, в предыдущем примере для определения числа k можно было просто разделить второй коэффициент −10 на 2

Пример 5. Решить квадратное уравнение

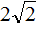
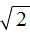
Коэффициент b равен . Это выражение состоит из множителя 2 и выражения . То есть оно уже представлено в виде 2k . Получается, что

Найдём дискриминант по формуле D₁ = k 2 − ac

Дискриминант больше нуля. Значит уравнение имеет два корня. Для их вычисления воспользуемся формулами и

При вычислении корня уравнения получилась дробь, в которой содержится квадратный корень из числа 2. Квадратный корень из числа 2 извлекается только приближённо. Если выполнить это приближённое извлечение, а затем сложить результат с 2, и затем разделить числитель на знаменатель, то получится не очень красивый ответ.

В таких случаях ответ записывают, не выполняя приближённых вычислений. В нашем случае первый корень уравнения будет равен .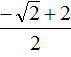

Вычислим второй корень уравнения:

Видео:5 способов решения квадратного уравнения ➜ Как решать квадратные уравнения?Скачать

Вывод формул

Давайте наглядно увидим, как появились формулы для вычисления корней квадратного уравнения с чётным вторым коэффициентом.

Рассмотрим квадратное уравнение ax 2 + bx + c = 0 . Допустим, что коэффициент b является чётным числом. Тогда его можно обозначить как 2k

Заменим в уравнении ax 2 + bx + c = 0 коэффициент b на выражение 2k

Теперь вычислим дискриминант по ранее известной формуле:

Вынесем в получившемся выражении за скобки общий множитель 4

Что можно сказать о получившемся дискриминанте? При чётном втором коэффициенте он состоит из множителя 4 и выражения k 2 − ac .

В выражении 4(k 2 − ac) множитель 4 постоянен. Значит знак дискриминанта зависит от выражения k 2 − ac . Если это выражение меньше нуля, то и D будет меньше нуля. Если это выражение больше нуля, то и D будет больше нуля. Если это выражение равно нулю, то и D будет равно нулю.

То есть выражение k 2 − ac это различитель — дискриминант. Такой дискриминант принято обозначать буквой D₁

Теперь посмотрим как выводятся формулы и .

В нашем уравнении ax 2 + bx + c = 0 коэффициент b заменён на выражение 2k . Воспользуемся стандартными формулами для вычисления корней. То есть формулами и . Только вместо b будем подставлять 2k . Также на забываем, что D у нас равно выражению 4(k 2 − ac)

Но ранее было сказано, что выражение k 2 − ac обозначается через D₁ . Тогда в наших преобразованиях следует сделать и эту замену:

Теперь вычислим квадратный корень, расположенный в числителе. Это квадратный корень из произведения — он равен произведению корней. Остальное перепишем без изменений:

Теперь в получившемся выражении вынесем за скобки общий множитель 2

Сократим получившуюся дробь на 2

Аналогично вывóдится формула для вычисления второго корня:

Видео:КВАДРАТНОЕ УРАВНЕНИЕ дискриминантСкачать

Как найти дискриминант квадратного уравнения

О чем эта статья:

Видео:Как решить квадратное уравнение за 30 секунд#математика #алгебра #уравнение #дискриминант #репетиторСкачать

Понятие квадратного уравнения

Уравнение — это равенство, содержащее переменную, значение которой нужно найти.

Например, х + 8 = 12 — это уравнение, содержащее переменную х.

Корень уравнения — это такое значение переменной, которое при подстановке в уравнение обращает его в верное числовое равенство.

Например, если х = 5, то при подстановке в уравнение мы получим:

13 = 12 — противоречие.

Значит, х = 5 не является корнем уравнения.

Если же х = 4, то при подстановке в уравнение мы получим:

12 = 12 — верное равенство.

Значит, х = 4 является корнем уравнения.

Решить уравнение — значит найти все его корни или доказать, что их не существует.

Квадратное уравнение — это уравнение вида ax2 + bx + c = 0, где a — первый или старший коэффициент, не равный нулю, b — второй коэффициент, c — свободный член.

Если все коэффициенты в уравнении отличны от нуля, то уравнение называется полным.

Такое уравнение можно решить с помощью формулы дискриминанта.

Видео:Как решать квадратные уравнения через дискриминант. Простое объяснениеСкачать

Понятие дискриминанта

Дискриминант квадратного уравнения — это выражение, равное b 2 − 4ac. Дискриминант в переводе с латинского означает «отличающий» или «различающий» и обозначается буквой D.

Дискриминант — отличный помощник, чтобы понять, сколько в уравнении корней.

Видео:Упрощенная формула корней квадратного уравнения. ЕГЭ и ОГЭ 2022 по математикеСкачать

Как решать квадратные уравнения через дискриминант

Алгоритм решения квадратного уравнения ax 2 + bx + c = 0:

Определим, чему равны коэффициенты a, b, c.

Вычислим значение дискриминанта по формуле D = b2 − 4ac.

Если дискриминант D 0, то у уравнения две корня, равные

Чтобы запомнить алгоритм решения полных квадратных уравнений и с легкостью его использовать, сохраните себе шпаргалку:

Видео:Формула корней квадратного уравнения. Алгебра, 8 классСкачать

Примеры решения квадратных уравнений с помощью дискриминанта

Пример 1. Решить уравнение: 3x 2 — 4x + 2 = 0.

1. Определим коэффициенты: a = 3, b = -4, c = 2.
2. Найдем дискриминант: D = b 2 — 4ac = (-4) 2 — 4 * 3 * 2 = 16 — 24 = -8.

Ответ: D 2 — 6x + 9 = 0.

1. Определим коэффициенты: a = 1, b = -6, c = 9.
2. Найдем дискриминант: D = b 2 — 4ac = (-6) 2 — 4 * 1 * 9 = 36 — 36 = 0.

D = 0, значит уравнение имеет один корень:

Ответ: корень уравнения 3.

Пример 3. Решить уравнение: x 2 — 4x — 5 = 0.

1. Определим коэффициенты: a = 1, b = -4, c = -5.
2. Найдем дискриминант: D = b 2 — 4ac = (-4) 2 — 4 * 1 * (-5) = 16 + 20 = 36.

D > 0, значит уравнение имеет два корня:

Ответ: два корня x₁ = 5, x₂ = -1.

Разобраться в решении квадратных уравнений на практике с классным преподавателем можно на курсах по математике в Skysmart.

Видео:Как решать любое квадратное уравнение Полное Неполное квадр ур x^2+2x-3=0 5x^2-2x=0 2x^2-2=0 3x^2=0Скачать

Дискриминант квадратного уравнения

Дискриминант квадратного уравнения — это выражение, находящееся под корнем в формуле нахождения корней квадратного уравнения. Дискриминант обозначается латинской буквой D.

Вид уравнения	Формула корней	Формула дискриминанта
ax 2 + bx + c = 0		b 2 — 4ac
ax 2 + 2kx + c = 0		k 2 — ac
x 2 + px + q = 0
		p 2 — 4q

Все формулы нахождения корней квадратных уравнений можно записать короче с помощью дискриминанта:

Вид уравнения	Формула
ax 2 + bx + c = 0	, где D = b 2 — 4ac
ax 2 + 2kx + c = 0	, где D = k 2 — ac
x 2 + px + q = 0	, где D =
	, где D = p 2 — 4q

Дискриминант позволяет определить, имеет ли уравнение корни и сколько их, не решая само уравнение:

1. Если дискриминант больше нуля, то уравнение имеет два корня.
2. Если дискриминант равен нулю, то уравнение имеет один корень.
3. Если дискриминант меньше нуля, то уравнение не имеет корней.

Несмотря на то, что есть несколько формул дискриминанта, чаще всего используют первую:

так как она относится к формуле:

,

которая является универсальной формулой нахождения корней квадратного уравнения. Данная формула подходит даже для неполных квадратных уравнений.

Видео:Квадратные уравнения от «А» до «Я». Классификация, решение и теорема Виета | МатематикаСкачать

Решение квадратных уравнений через дискриминант

Для решения квадратного уравнения по формуле можно сначала вычислить дискриминант и сравнить его с нулём. В зависимости от результата, либо искать корни по формуле, либо сделать вывод, что корней нет.

Пример 1. Решить уравнение:

Определим, чему равны коэффициенты:

D = b 2 — 4ac = (-4) 2 — 4 · 3 · 2 = 16 — 24 = -8,

Определим, чему равны коэффициенты:

D = b 2 — 4ac = (-6) 2 — 4 · 1 · 9 = 36 — 36 = 0,

Уравнение имеет всего один корень:

Определим, чему равны коэффициенты:

D = b 2 — 4ac = (-4) 2 — 4 · 1 · (-5) = 16 + 20 = 36,

🔍 Видео

Решение квадратных уравнений. Дискриминант. Практическая часть. 1ч. 8 класс.Скачать

Быстрый способ решения квадратного уравненияСкачать

Как решать квадратные уравнения без дискриминантаСкачать

Квадратный Трехчлен / Разложение квадратного трехчлена на множители, Как решать Квадратные УравненияСкачать

Квадратное уравнение, дискриминант, формула корнейСкачать

Решение биквадратных уравнений. 8 класс.Скачать

8 класс, 25 урок, Формула корней квадратного уравненияСкачать

Как решать квадратные уравнения через дискриминант | МатематикаСкачать

Квадратное уравнение. Как решить? | Математика ОГЭ 2023 | УмскулСкачать

Как решать квадратные уравнения. 8 класс. Вебинар | МатематикаСкачать