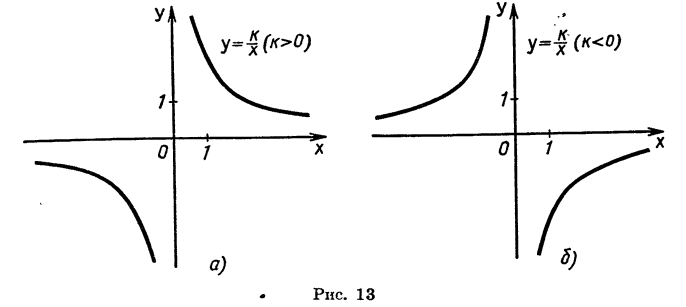
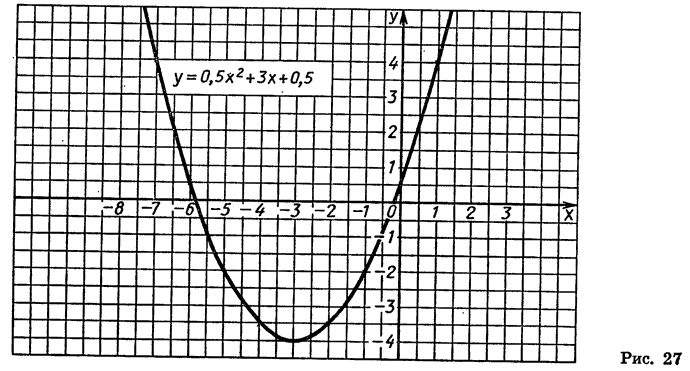
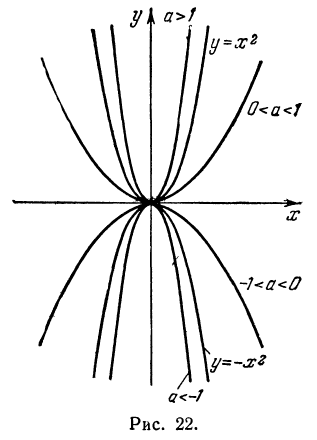
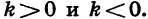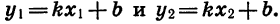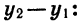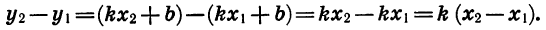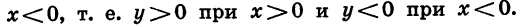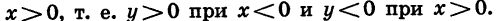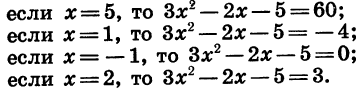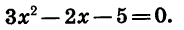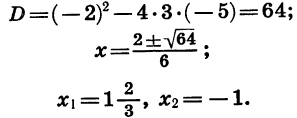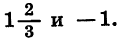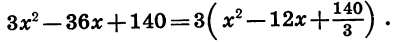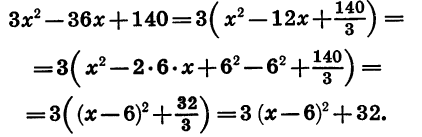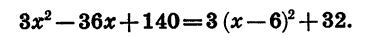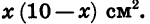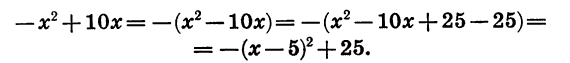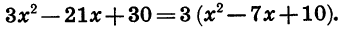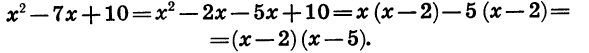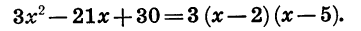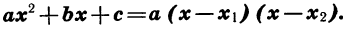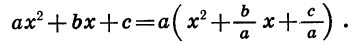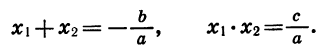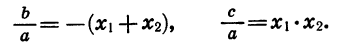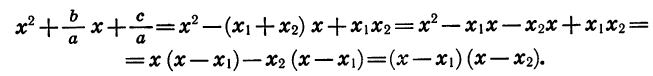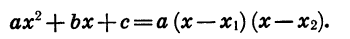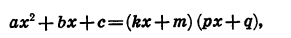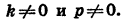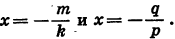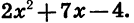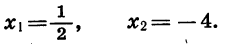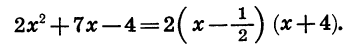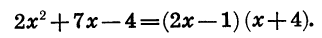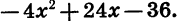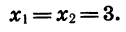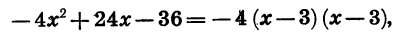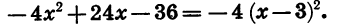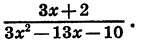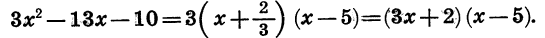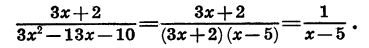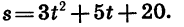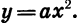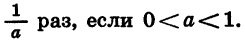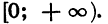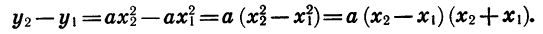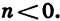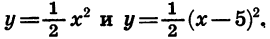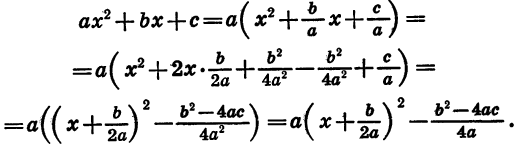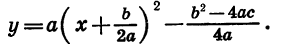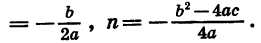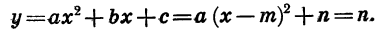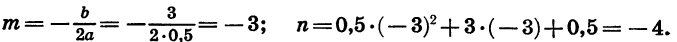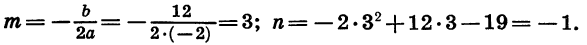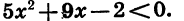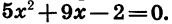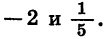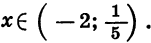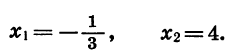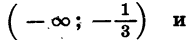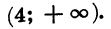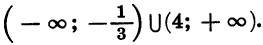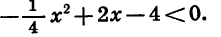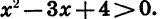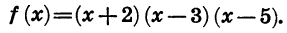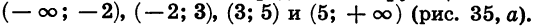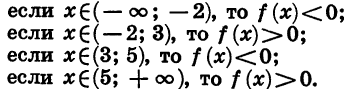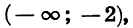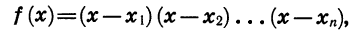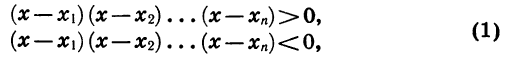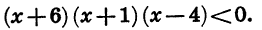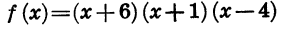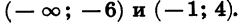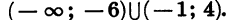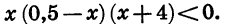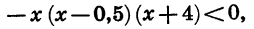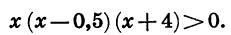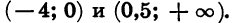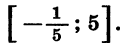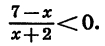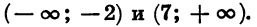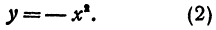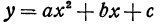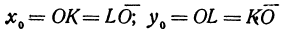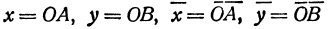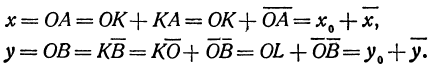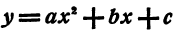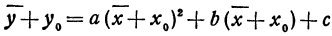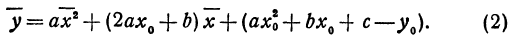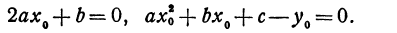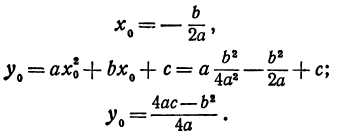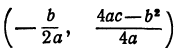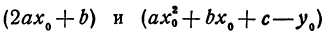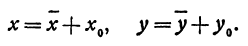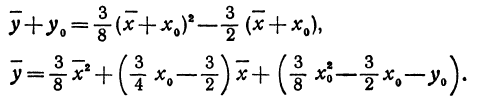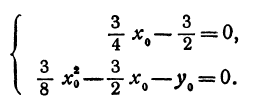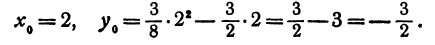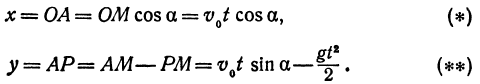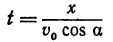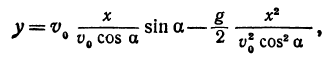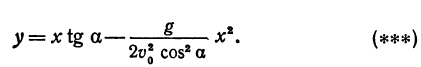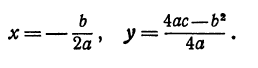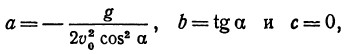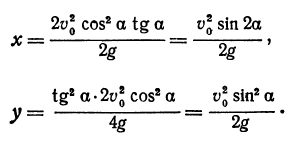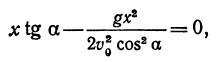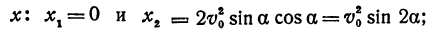Квадратичная функция — целая рациональная функция второй степени вида 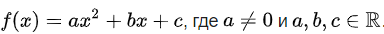
- Формула корней квадратного уравнения
- Дискриминант
- Трёхчлен второй степени
- Разложение трёхчлена второй степени
- График квадратной функции
- График функции у=x²
- График функции у= x²
- График функции y=ax²+b
- Биквадратное уравнение
- Уравнения, левая часть которых разлагается на множители, а правая есть нуль
- Двучленное уравнение
- Решение двучленных уравнений третьей степени
- Различные значения корня
- Системы уравнений второй степени
- Системы двух уравнений, из которых одно первой степени, а другое—второй
- Система двух уравнений, из которых каждое второй степени
- Графический способ решения систем уравнений второй степени
- Квадратичная функция — основные понятия и определения
- Свойства функции
- Квадратный трехчлен
- Квадратный трехчлен и его корни
- Разложение квадратного трехчлена на множители
- Квадратичная функция и ее график
- Решение неравенств второй степени с одной переменной
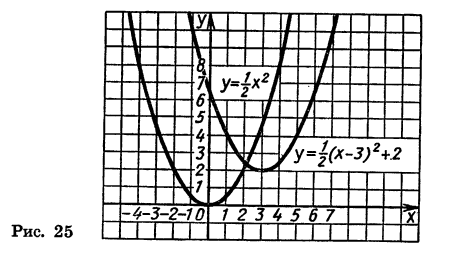
- Квадратичная функция и её построение
- Парабола
- Параллельный перенос осей координат
- Исследование функции
- Графическое решение квадратных уравнений
- Презентация по математике «Графическое решение квадратных уравнений» (8 класс)
- Описание презентации по отдельным слайдам:
- Краткое описание документа:
- Охрана труда
- Библиотечно-библиографические и информационные знания в педагогическом процессе
- Охрана труда
- Дистанционные курсы для педагогов
- Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
- Другие материалы
- Оставьте свой комментарий
- Автор материала
- Дистанционные курсы для педагогов
- Подарочные сертификаты
- 📸 Видео
Видео:Решение квадратных неравенств графическим методом. 8 класс.Скачать

Формула корней квадратного уравнения
В первой части курса были выведены следующие формулы для определения корней неполного и полного квадратных уравнений:
1) αx²=0; очевидно, оба корня уравнения равны нулю.
2) αx²+с=0; формула для корней будет: 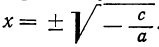
3) αx² +bx=0; тогда x₁ =0; х₂ = 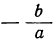
4) x² + +q=0; формула корней даёт:
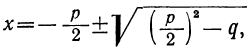
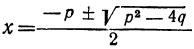
5) Наконец, общая формула для корней полного квадратного уравнения вида αx²+bx+c=0 будет:
Последняя формула является наиболее общей; из неё как частные случаи получаются все остальные. Так, полагая в этой формуле α=l, получаем случай (4) (в этом случае b=p и c=q); полагая с=0, получаем случай (3); при b=0 будем иметь случай (2) и, наконец, первый случай получим, давая в общей формуле значения b=c=0.
Дискриминант
Рассмотрим различные случаи, которые могут встретиться при решении квадратного уравнения в зависимости от числового значения коэффициентов.
1. b² — 4αc>0. В этом случае выражение под корнем положительно. Квадратный корень из него имеет два значения, и, следовательно, уравнение имеет два различных вещественных корня:
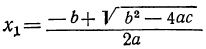
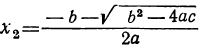
2. b² — 4αc=0. В этом случае второй член числителя равен нулю, и уравнение имеет два равных корня:
3. b² — 4αc Свойства корней квадратного уравнения (теорема Виета)
Возьмём формулу корней квадратного уравнения, у которого коэффициент при x² равен единице, т. е. уравнения вида x²+ +q=0:
Если сложим почленно эти равенства, то радикалы взаимно уничтожатся, и мы получим:
Если те же равенства почленно перемножим, то получим (произведение суммы двух чисел на их разность равно разности квадратов этих чисел):
Каково бы ни было подкоренное число, всегда
Следовательно:
Таким образом:
Сумма корней приведённого квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение этих корней равно свободному члену.
Теперь возьмём квадратное уравнение общего вида αx²+bx+c=0. Разделив все его члены на а, мы приведём это уравнение к только что рассмотренному виду:
следовательно, для неприведённого полного уравнения мы должны иметь:
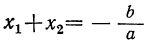
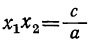
Следствия:
1) Пользуясь этими свойствами, мы легко можем составить квадратное уравнение, у которого корнями были бы данные числа.
Пусть, например, надо составить уравнение, у которого корни были бы числа 2 и 3. Тогда из равенства 2+3= — р и 2∙3 = q находим: р = — 5 и q=6; следовательно, уравнение будет: x²-5x+6=0.
Подобно этому найдём,что 3 и -7 будут корни уравнения x²- [3+(- 7)]x+3( -7) = 0, т. е. x²+4x-21=0; числа 3 и 0 будут корни уравнения x²— 3x=0.
2) При помощи тех же свойств мы можем, не решая квадратного уравнения, определить знаки его корней, если эти корни вещественные. Пусть, например, имеем уравнение x²+8x+12=0. Так как в этом примере выражение 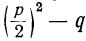
Трёхчлен второй степени
Выражение αx²+bx+c, в котором х означает независимое переменное, а α, b и с — какие-нибудь данные, постоянные числа, называется квадратной функцией, или трёхчленом второй степени. Различие между таким трёхчленом и левой частью уравнения αx²+bx+c=0 состоит в том, что в уравнении буква х означает только те числа, которые удовлетворяют уравнению, тогда как в трёхчлене она означает какое угодно число. Значения х, обращающие трёхчлен в нуль, называются его корнями; значит, корни трёхчлена-это корни квадратного уравнения:
αx² +6x+c=0.
В частном случае при α=1 трёхчлен принимает вид: x²+ +q; при b=0 или при с=0 трёхчлен обращается в двучлен αx²+c или αx²+bx.
Разложение трёхчлена второй степени
Сначала возьмём трёхчлен x²+ +q, в котором коэффициент при x² есть 1. Решив приведённое уравнение x²+ +q=0, мы найдём корни его х₁ и х₂ . Как мы сейчас видели: х₁+х₂ =-p и х₁х₂ =q.
Таким образом:
Трёхчлен x² +q разлагается на два множителя, из которых первый равен разности между х и одним корнем трёхчлена, а второй равен разности между х и другим корнем трёхчлена.
Примеры:
Теперь возьмём трёхчлен αx²+bx+c, в котором коэффициент при x² есть какое угодно число. Этот трёхчлен можно представить так:
Выражение, стоящее внутри скобок, есть трёхчлен вида x²+ +q . Его корни х₁ и х₂ будут те же самые, что трёхчлена αx²+bx+c. Найдя их, мы можем, по доказанному, разложить этот трёхчлен так: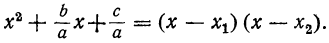
Следовательно: αx²+bx+c =α(x — х₁) (х — х₂).
Таким образом, разложение трёхчлена αx²+bx+c отличается от разложения трёхчлена x²+ +q только дополнительным множителем α.
Примеры:
1) Трёхчлен 2x² — 2х -12, корни которого 3 и — 2, можно разложить так: 2(x — 3)(x+2).
2) Трёхчлен 3x² + х +1, корни которого следующие:
разлагается так:
3) 6abx² — ( 3b³ +2α³)x+a²b² .
Корни этого трёхчлена следующие:
Поэтому:
4) Сократить дробь:
Разложим числитель и знаменатель на множители и затем, если можно, сократим дробь. Так как корни числителя 3 и —2, а корни знаменателя 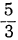
Следствие:
По данным корням можно составить квадратное уравнение. Так, уравнение, имеющее корни З и -2, будет:
(x-3)[x-( — 2)] =0, т. е. (х — 3)(x+2)=0,
что по раскрытии скобок даёт: x² — х — 6 = 0. Конечно, все члены этого уравнения можно умножить на произвольное число, не зависящее от х (например, на 2), отчего корни не изменятся.
Сократить следующие дроби (предварительно разложив числитель и знаменатель каждой дроби на множители):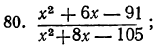
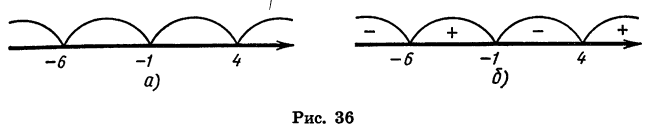
Разложив на множители следующие трёхчлены, определить, для каких значений х эти трёхчлены будут давать положительные числа и для каких — отрицательные:
Видео:АЛГЕБРА 8 класс : Графическое решение квадратных уравнений | ВидеоурокСкачать

График квадратной функции
Графиком квадратичной функции является парабола.
График функции у=x²
Обратим внимание на следующие особенности функции y=x²;
а) При всяком значении аргумента х функция определена и получает только одно значение. Например, при x = — 10 значение функции будет (-10)² = 100, при x = 1000 значение функции будет 1000² = 1 000 000 и т. п.
б) Так как (—x)² =x² , то при двух значениях х, отличающихся только знаками, получаются два одинаковых положительных значения у; например, при х = — 2 и при x =+2 значение у будет одно и то же, именно 4. Отрицательных значений для у никогда не получается.
в) Если абсолютная величина х неограниченно увеличивается, то и у неограниченно увеличивается. Так, если для х будем давать ряд неограниченно возрастающих положительных значений: 1, 2, 3, 4,… или ряд неограниченно убывающих отрицательных значений: -1, -2, -3, -4, … ,то для у получим ряд неограниченно возрастающих значений: 1, 4, 9, 16, 25, … .
Заметив эти свойства, составим таблицу значений функции у= x²; например, такую:
| x | … | -2 | -1,5 | -1 | -0,5 | 0 | 0,5 | 1 | 1,5 | 2 | … |
| у | … | 4 | 2,25 | 1 | 0,25 | 0 | 0,25 | 1 | 2,25 | 4 | … |
Изобразим теперь эти значения на чертеже 16 в виде точек, абсциссы которых будут выписанные значения х, а ординаты — соответствующие значения у (на чертеже за единицу длины мы приняли отрезок O1); полученные точки соединим кривой. Кривая эта называется параболой. Рассмотрим некоторые её свойства:
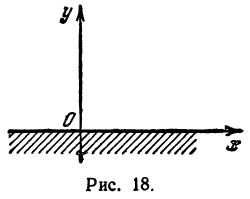
а) Вся кривая расположена по одну сторону от оси х-ов, именно — по ту сторону, по какую лежат положительные значения ординат.
б) Парабола разделяется осью у-ов на две части (ветви). Точка О, в которой эти ветви сходятся, называется вершиной параболы. Эта точка есть единственная общая точка параболы и оси х-ов.
в) Обе ветви бесконечны, так как х и у могут увеличиваться беспредельно. Ветви поднимаются от оси х-ов неограниченно вверх, удаляясь в то же время неограниченно от оси у-ов вправо и влево.
г) Ось у-ов служит для параболы осью симметрии, так что если перегнуть чертёж по этой оси так, чтобы левая половина чертежа упала на правую, то обе ветви совместятся; например, точка с абсциссой — 2 и с ординатой 4 совместится с точкой, имеющей абсциссу +2 и ту же ординату 4.
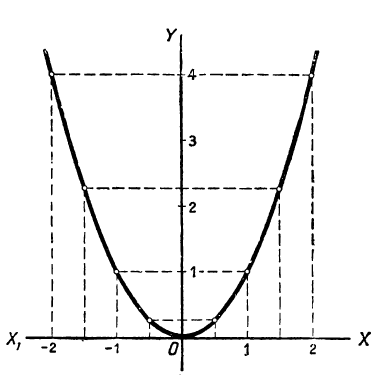
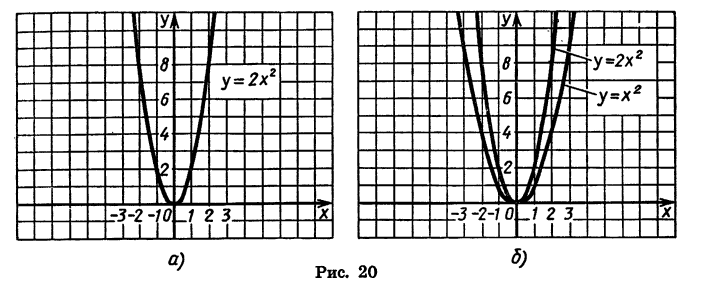
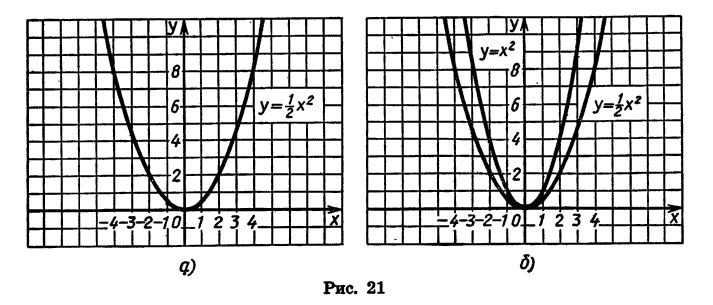
График функции у= x²
Предположим сначала, что а есть число положительное. Возьмём, например, такие две функции:
Составим таблицы значений этих функций, например такие:
| x | -2 | -1 | 0 | 1 | 2 | … |
| у | 6 | 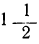 | 0 | 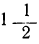 | 6 | … |
| x | -3 | -2 | -1 | 0 | 1 | 2 | … |
| у | 3 | 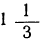 | 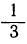 | 0 | 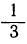 | 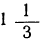 | … |
Нанесём все эти значения на чертёж 17 и проведём кривые. Для сравнения мы поместили на том же чертеже (прерывистой линией) ещё график функции: 3) y=x² .
| x | -2 | -1 | 0 | 1 | 2 | … |
| y | 4 | 1 | 0 | 1 | 4 | … |
Из чертежа видно, что при одной и той же абсциссе ордината первой кривой в 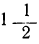
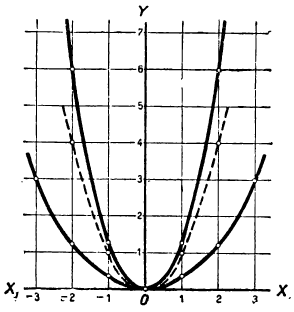
Замечание:
Если зависимость между двумя переменными величинами у и х выражается равенством y=ax² , где a — какое-нибудь постоянное число, то можно сказать, что величина у пропорциональна квадрату величины х, так как с увеличением или уменьшением х в 2 раза, в 3 раза и т. д. величина у увеличивается или уменьшается в 4 раза, в 9 раз, в 16 раз и т. д.
Например, площадь круга равна πR² , где R есть радиус круга и π — постоянное число; поэтому можно сказать, что площадь круга пропорциональна квадрату его радиуса.
График функции y=ax²+b
Пусть мы имеем следующие три функции:
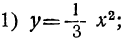
Очевидно, что при одном и том же значении аргумента х ордината второй функции больше, а ордината третьей функции меньше на 2 единицы, чем соответствующая ордината первой функции. Поэтому вторая и третья функции изобразятся на чертеже той же параболой, что и первая функция, только парабола эта должна быть поднята вверх (для второй функции) и опущена вниз (для третьей функции) на 2 единицы длины.
Вообще график функции y=ax²+b есть та же парабола, которая изображает функцию у=ax², только парабола эта должна быть поднята вверх, если b>0, опущена вниз, если b График трёхчлена второй степени
Сначала мы рассмотрим график такого трёхчлена, который может быть представлен в виде произведения a (x+m)² . Например, возьмём такие две функции:
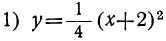
Для сравнения изобразим на том же чертеже ещё параболу:
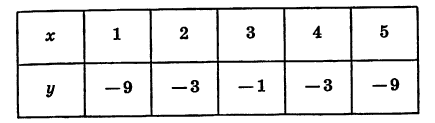
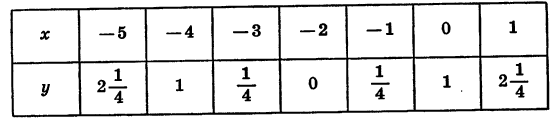
Предварительно составим таблицу частных значений этих трёх функций; например, такую:
| x= | -5 | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
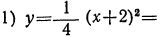 | 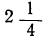 | 1 | 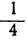 | 0 | 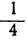 | 1 | 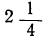 | 4 | 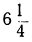 | 9 | 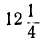 | 16 |
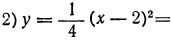 | 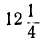 | 9 | 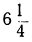 | 4 | 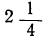 | 1 | 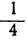 | 0 | 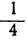 | 1 | 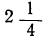 | 4 |
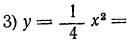 | 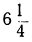 | 4 | 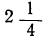 | 1 | 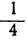 | 0 | 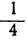 | 1 | 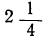 | 4 | 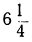 | 9 |
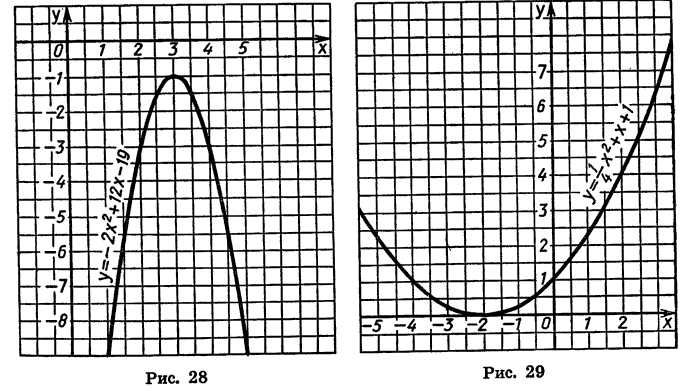
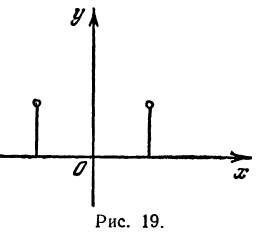
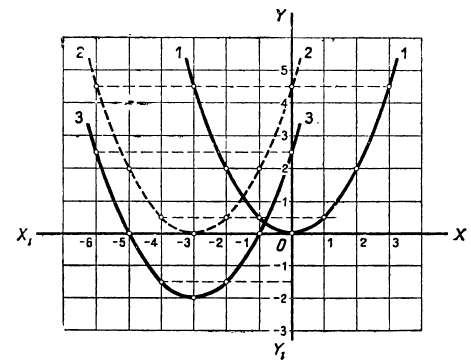
Нанеся все эти значения на чертёж, получим три графика, изображённые на чертеже 19.
Рассматривая этот чертёж, мы замечаем, что кривая 1 есть та же парабола 3, только перенесённая на 2 единицы влево, а кривая 2 есть та же парабола 3, но перенесённая на 2 единицы вправо.
Обобщая этот вывод, мы можем сказать, что график функции y=a(x+m)² есть парабола, изображающая функцию y=ax² , только парабола эта перенесена влево, если m>0, и в правд, если m 0, как в наших примерах, и вниз, если α Графический способ решения квадратного уравнения
Квадратное уравнение можно графически решить таким способом:
построив на миллиметровой бумаге параболу, изображающую трёхчлен, стоящий в левой части уравнения, находим точки пересечения этой параболы с осью х-ов. Абсциссы этих точек и будут корни уравнения, так как при этих абсциссах ординаты, изображающие соответствующие значения трёхчлена, равны нулю.
Примеры:
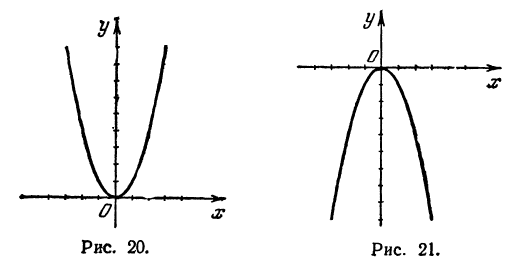
График левой части этого уравнения изображён кривой 3 (черт. 20). На нём мы видим, что парабола пересекается с осью х-ов в двух точках, абсциссы которых —1 и —5. Это и будут корни уравнения.
Это можно проверить, решив уравнение посредством общей формулы или путём подстановки.
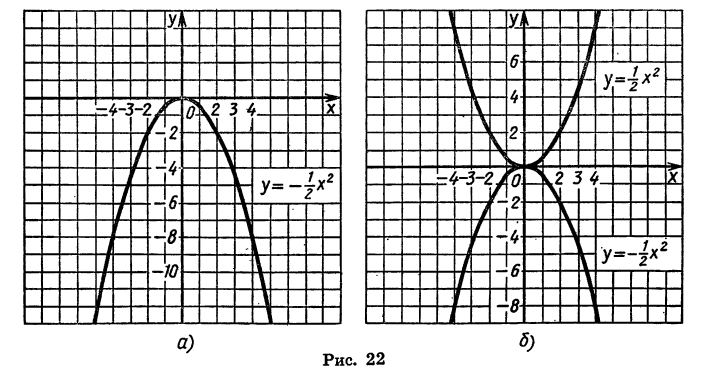
Составив таблицу частных значений трёхчлена
| x | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | … |
| y | 8 | 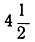 | 2 | 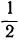 | 0 | 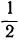 | 2 | 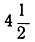 | 8 | … |
мы построим параболу (черт. 21). Эта парабола не пересекается с осью х-ов, а только её касается в точке с абсциссой 2. Уравнение в этом случае имеет только один корень 2 (точнее, два равных корня).
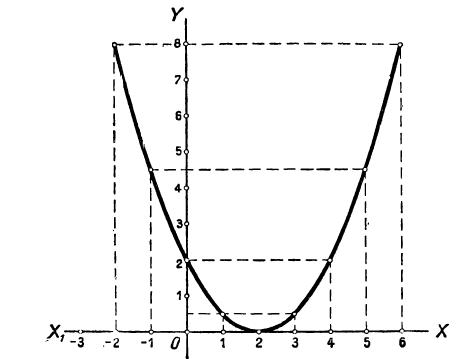
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | … |
| y | 14 | 8 | 4 | 2 | 2 | 4 | 8 | 14 | … |
Парабола (черт. 22) не пересекается и не касается оси х-ов; уравнение не имеет вещественных корней.
Укажем ещё следующий приём графического решения квадратного уравнения. Пусть требуется решить уравнение:
x² — 1,5х — 2=0.
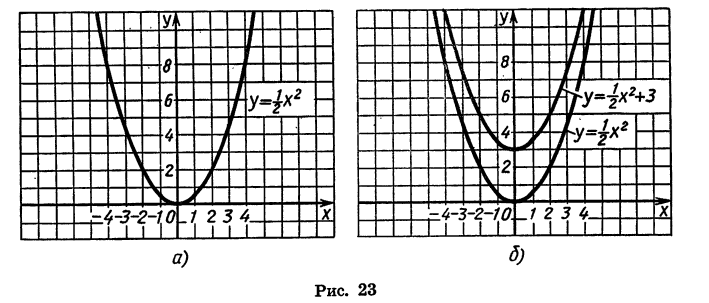
Каждая часть этого уравнения, рассматриваемая отдельно, есть некоторая функция от х. Обозначим функцию, выражаемую левой частью уравнения, буквой y₁ , а функцию, выражаемую правой частью уравнения, буквой у₂ . Первая функция на чертеже 23 изобразится параболой, а вторая — прямой. Построив на одном и том же чертеже графики этих двух функций, мы найдём, что прямая и парабола пересекаются в двух точках, абсциссы которых приблизительно выражаются числами 2,35 и — 0,85. Это и будут приближённые значения корней данного уравнения, так как при каждой из этих абсцисс ординаты y₁, у₂ равны между собой, и, следовательно, x² =l,5x+2.
Если случится, что прямая с параболой не пересекается, то уравнение не имеет вещественных корней; если же прямая коснётся параболы, то уравнение имеет один корень, равный абсциссе точки касания.
Биквадратное уравнение
Уравнение четвёртой степени, например такое:
x⁴ — 13x² + 36=0,
в которое входят только чётные степени неизвестного, называется биквадратным. Оно приводится к квадратному, если заменим х² через у и, следовательно, x⁴ через у² ; тогда уравнение обратится в квадратное:
у² — 13y+36=0.
Решим его:
Но из равенства x²=y видно, что x=± √y. Подставляя сюда на место у найденные числа 9 и 4, получим следующие четыре решения данного уравнения:
x₁ = +√ 9 = 3;
x₂ = -√ 9 = -3;
x₃ = + √4 =2;
x₃ = — √4 = -2.
Составим формулы для решения биквадратного уравнения общего вида:
ax⁴ +bx² + c=0.
Положив x²=y, получим уравнение ay² + by + c=0, из которого находим:
Но так как x=± √y , то для биквадратного уравнения мы получим следующие четыре решения:
Отсюда видно, что если b² — 4ac 0, то могут быть три случая (мы полагаем a > 0):
1) все корни вещественные (как в приведённом выше численном примере), если 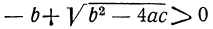
2) все корни мнимые, если оба эти выражения дадут отрицательные числа, и 3) два корня вещественные и два мнимые, если 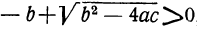
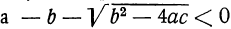
Уравнения, левая часть которых разлагается на множители, а правая есть нуль
Решение таких уравнений сводится к решению уравнений более низких степеней. Так, мы видели, что для решения неполного квадратного уравнения вида ax² + bx=0 достаточно его левую часть разложить на два множителя: x(ax + b) = 0 и затем, приняв во внимание, что произведение равно нулю только тогда, когда какой-нибудь сомножитель равен нулю, свести решение этого уравнения к решению двух уравнений первой степени: x=0 и ax + b=0.
Подобно этому можно решить неполное кубическое уравнение, не содержащее свободного члена; например, такое:
x³ + 3x² — 10x = 0.
Вынеся х за скобки, мы представим уравнение так:
x (x² +3x — 10) = 0,
из которых находим три решения:
Пусть некоторое уравнение приведено к такому виду:
x(x+4)(x²-5x+6)=0.
Тогда оно распадается на три уравнения:
x = 0; x + 4 = 0; x² — 5x + 6 = 0
Двучленное уравнение
Двучленным уравнением называется уравнение вида 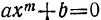
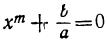
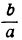
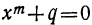
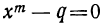
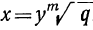
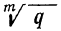
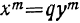
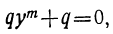
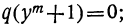
или
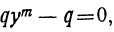
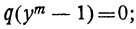
Итак, решение двучленных уравнений приводится к решению уравнений вида 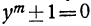
Решение двучленных уравнений третьей степени
Эти уравнения следующие: х³ —1=0 и х³ + l=0.
мы можем предложенные уравнения записать так:
(х -1)(x² + х +1) = 0 и ( х +1 ) ( x² — х +1)=0.
Значит, первое из них имеет своими корнями корни уравнений: x-1=0 и x²+ x +1=0, а второе — корни уравнений: x+1=0 и x²- x +1=0.
Решив их, находим, что уравнение х³ — 1=0 имеет следующие три корня:
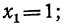
из которых один вещественный, а два мнимых; уравнение х³ + 1 = 0 имеет три корня:

из которых также один вещественный и два мнимых.
Различные значения корня
Решение двучленных уравнений имеет тесную связь с нахождением всех значений корня (радикала) из данного числа. В самом деле, найти 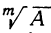
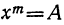
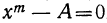
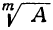
Основываясь на этом замечании, покажем, например, что корень кубичный из всякого вещественного числа (не равного нулю) имеет три различных значения.
Рассмотрим сначала случай положительного числа А. Пусть требуется найти 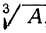
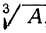
Мы видели, что это уравнение имеет три
корня: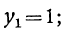
Каждое из этих значений, удовлетворяя уравнению y³ = l, представляет собой кубичный корень из 1. Так как x=qy, то
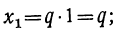
Это и будут три значения 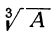
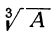
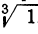
Например, кубичный корень из 8 имеет три следующих значения:
Если A Трёхчленное уравнение
Так называется уравнение вида: 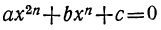
(частный случай такого вида при n=2 есть биквадратное уравнение). Оно приводится к квадратному, если введём вспомогательное неизвестное 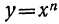
ay²+by+c=0,
откуда:
Следовательно:
Решив, если возможно, это двучленное уравнение, найдём все значения х.
Пример:
x⁶- 9x³ + 8=0.
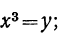
y₁=8; y₂=1;
следовательно:
x³=8 и x³=1.
Решив эти двучленные уравнения третьей степени, получим шесть значений для х:
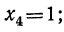
Видео:8 класс, 21 урок, Графическое решение уравненийСкачать

Системы уравнений второй степени
Степень уравнения с несколькими неизвестными: Чтобы определить степень уравнения, в которое входят несколько неизвестных, надо предварительно это уравнение упростить (раскрыть скобки, освободить от радикалов и знаменателей, которые содержат неизвестные, и сделать приведение подобных членов). Тогда степенью уравнения называется сумма показателей при неизвестных в том члене уравнения, в котором эта сумма наибольшая.
Например, три уравнения: x²+2xy—x+2=0, 3xy=4, 2x+y² — у=0 будут уравнениями второй степени с двумя неизвестными; уравнение 3x²y—y² + x+10 = 0 есть уравнение третьей степени (с двумя неизвестными) и т. п.
Заметим, что сумма показателей при неизвестных в каком-нибудь члене уравнения называется его измерением. Так, члены 2xy, 5x² , Зу² — второго измерения, члены 0,2x²y, 10xy² , 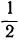
Заметим ещё, что уравнение называется однородным, если все его члены — одного и того же измерения. Так, 3x² + xy — 2y²=0 есть однородное уравнение второй степени с двумя неизвестными.
Мы рассмотрим сейчас, как решаются некоторые простейшие системы уравнений второй степени с двумя неизвестными.
Общий вид полного уравнения второй степени с двумя неизвестными есть следующий:
ax² +bxy+cy² +dx+ey+j=0.
В нём первые три члена — второго измерения, следующие два члена — первого и последний (свободный) член — нулевого. Коэффициенты а, b, с, … могут быть числами положительными, отрицательными, а также равными нулю (конечно, три коэффициента а, b и с не предполагаются одновременно равными нулю, так как в противном случае уравнение было бы не второй, а первой степени).
Мы рассмотрим сейчас, как решаются простейшие системы двух уравнений второй степени с двумя неизвестными.
Системы двух уравнений, из которых одно первой степени, а другое—второй
Пусть дана система:
Всего удобнее такую систему решить способом подстановки следующим путём. Из уравнения первой степени определяем одно какое-нибудь неизвестное как функцию от другого неизвестного; например, определяем у как функцию от х:
y=2x — 1.
Тогда уравнение второй степени после подстановки даёт уравнение с одним неизвестным х:
x² — 4(2x — l)² + x +3(2x — 1) = 1;
x² — 4(4x² — 4x + l)+x+6x— 3=1;
x² — 16x² +16x — 4 + x + 6x — 3 — 1=0;
— 15 x² — 23x-8=0; 15x² — 23x + 8=0;
После этого из уравнения у=2х — 1 находим:
Таким образом, данная система имеет два решения:
Искусственные приёмы:
Указанный приём применим в тех случаях, когда одно уравнение первой степени; в некоторых случаях можно пользоваться искусственными приёмами, для которых нельзя указать общего правила. Приведём примеры.
Пример:
Первый способ. Так как даны сумма и произведение неизвестных, то х и у должны быть корнями квадратного уравнения:
z² — az + b =0.
Следовательно:
Второй способ. Возвысим первое уравнение в квадрат и вычтем из них учетверённое второе:
x²+ 2xy + y² = a²
т.е.
(x-y)² =a²— 4b, откуда
Теперь мы имеем систему:
Складывая и вычитая эти уравнения, получим:
Так как одно из данных уравнений мы возвышали в квадрат, то проверяем подстановкой, нет ли посторонних корней в числе найденных.
Таким образом находим, что данная система имеет два решения:
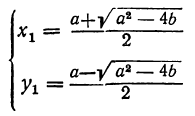
Второе решение отличается от первого только тем, что значение х в первом решении служит значением у во втором решении, и наоборот. Это можно было предвидеть, так как данные уравнения не изменяются от замены х на у, а у на х. Заметим, что такие уравнения называются симметричными.
Пример:
х — y= a, xy=b.
Первый способ. Представив уравнения в виде:
x +( —y)=а, x (-y)=-b,
замечаем, что х и —у это корни квадратного уравнения:
z² -az-b=0,
следовательно:
Второй способ. Возвысив первое уравнение в квадрат и сложив его с учетверённым вторым, получим:
(x + y)² = α² + 4b, откуда
Теперь имеем систему:
Пример:
x+y=cz, x² + y² = 6.
Возвысив первое уравнение в квадрат и вычтя из него второе, получим:
2xy= a² — b, откуда
Теперь вопрос приводится к решению системы:
x + y= a,
которую мы уже рассмотрели в первом примере.
Система двух уравнений, из которых каждое второй степени
Такая система в общем виде не разрешается элементарно, так как она приводится к полному уравнению четвёртой степени.
Рассмотрим некоторые частные виды уравнений, которые можно решить элементарным путём.
Пример:
x² +y² =α, ху=b.
Первый способ (способ подстановки). Из второго уравнения определяем одно неизвестное в зависимости от другого; например, 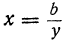
у⁴ — αy² + b² =0.
Решив его, найдём для у четыре значения. Подставив каждое из них в формулу, выведенную ранее для х, найдём четыре соответствующих значения для х.
Второй способ. Сложив первое уравнение с удвоенным вторым, получим:
x² +y² +2xy=α+2b, т. е. (x + y)² =a + 2b,
откуда:
откуда:
Таким образом, вопрос приводится к решению следующих четырёх систем первой степени:
Каждая из них решается весьма просто посредством алгебраического сложения уравнений.
Третий способ. Возвысив второе уравнение в квадрат, получим следующую систему:
x² + y² =α, x²y² =b².
Отсюда видно, что x² и y² — корни квадратного уравнения:
z² + az+b² =0.
Следовательно:
Пример:
x² — y² = a, xy=b.
Способом подстановки легко приведём эту систему к биквадратному уравнению. Вот ещё искусственный’приём решения этой системы.
Отсюда видно, что x² и — y² будут корнями уравнения:
z² — az — b² = 0.
Следовательно:
Замечание:
Во всех случаях, когда приходится возводить уравнения в степень, необходима проверка корней.
Графический способ решения систем уравнений второй степени
Начертив графики каждого из данных уравнений, находим величины координат точек пересечения этих графиков; это и будут корни уравнений.
Пример:
Составим таблицу частных значений х и у для первого уравнения:
| x | … | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 | … |
| y | … | 20 | 12 | 6 | 2 | 0 | 0 | 2 | 6 | 12 | … |
и таблицу частных значений х и у для второго уравнения:
| x | … | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | … |
| y | … | 15 | 5 | -1 | -3 | -1 | 5 | 15 | 29 | … |
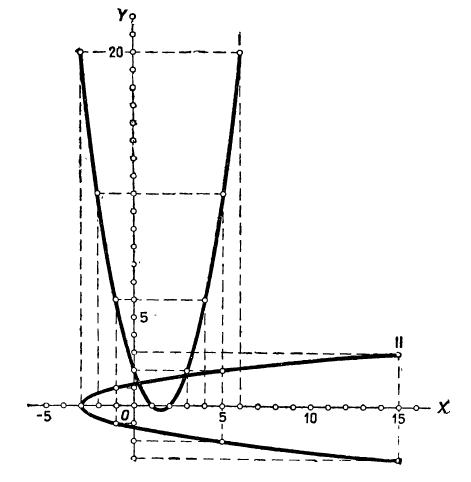
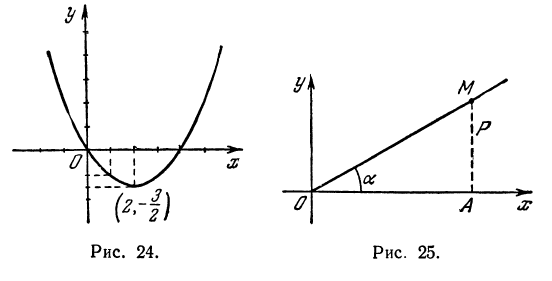
По этим значениям построим графики (эти графики будут параболы, черт. 24).
Графики пересекаются в двух точках, координаты которых приблизительно будут: х=0,3; y=1,3 и x=2,8; y=l,6.
Можно найти координаты точек пересечения точнее, если начертим в более крупном масштабе те части графиков, которые лежат около точек пересечения.
Видео:7 класс, 35 урок, Графическое решение уравненийСкачать

Квадратичная функция — основные понятия и определения
Функция — одно из важнейших математических понятий. Напомним, что функцией называют такую зависимость переменной у от переменной х, при которой каждому значению переменной х соответствует единственное значение переменной у.
Переменную х называют независимой переменной или аргументом. Переменную у называют зависимой переменной. Говорят также, что переменная у является функцией от переменной х. Значения зависимой переменной называют значениями функции.
Если зависимость переменной у от переменной х является функцией, то коротко это записывают так: y = f(x). (Читают: у равно / от х.) Символом / (х) обозначают значение функции, соответствующее значению аргумента, равному х.
Пусть, например, функция задается формулой 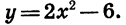
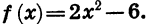
Заметим, что в записи вида y = f(x) вместо f употребляют и другие буквы: 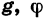
Все значения независимой переменной образуют область onределения функции. Все значения, которые принимает зависимая переменная, образуют область значений функции.
Если функция задана формулой и ее область определения не указана, то считают, что область определения функции состоит из всех значений аргумента, при которых формула имеет смысл. Например, областью определения функции 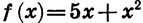
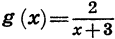
Область определения функции, описывающей реальный процесс, зависит от конкретных условий его протекания. Например, зависимость длины l железного стержня от температуры нагревания t выражается формулой 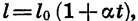
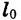
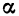
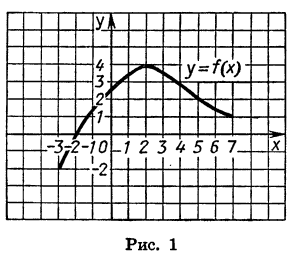
Напомним, что графиком функции называют множество всех точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты — соответствующим значениям функции.
На рисунке 1 изображен график функции y = f(x), областью определения которой является промежуток [ — 3; 7]. С помощью графика можно найти, например, что f(— 3) = — 2, f(0) = 2,5, f(2) = 4, f(5) = 2. Наименьшее значение функции равно —2, а наибольшее равно 4; при этом любое число от —2 до 4 является значением данной функции. Таким образом, областью значений функции y = f(x) служит промежуток [-2; 4].
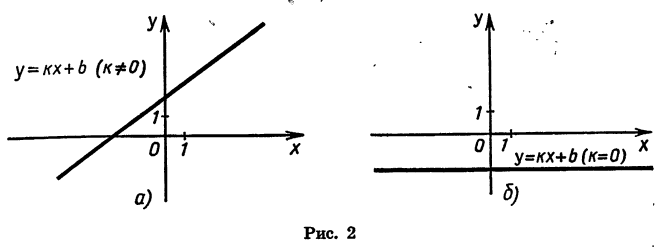
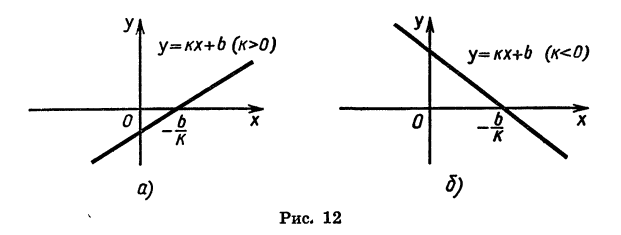
Мы изучили некоторые важные виды функций: линейную функцию, т. е. функцию, задаваемую формулой 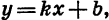
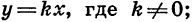
Графиком функции 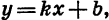
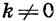
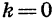
График функции 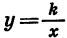
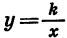

Функциями такого вида описываются многие реальные процессы и закономерности. Например, прямой пропорциональностью является зависимость массы тела m от его объема V при постоянной плотности 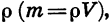
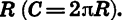
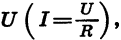
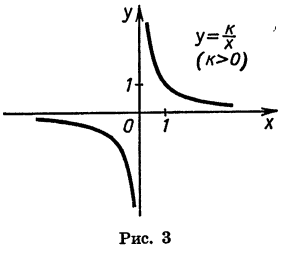
Мы рассматривали также функции, заданные формулами 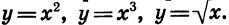
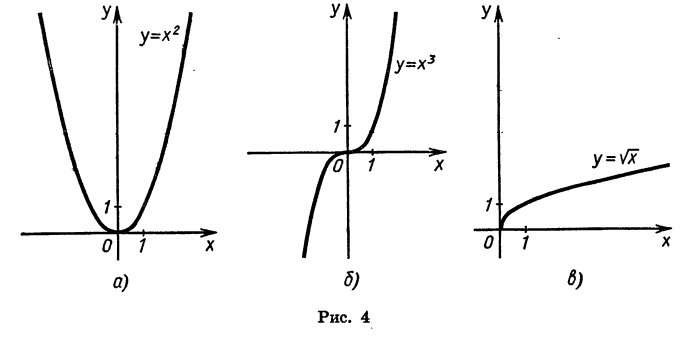
Рассмотрим еще одну функцию, а именно функцию, заданную формулой
Так как выражение |х| имеет смысл при любом х, то областью определения этой функции является множество всех чисел. По определению |х| = х, если 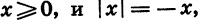
График рассматриваемой функции в промежутке
совпадает с графиком функции у = х, а в промежутке 
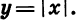
Свойства функции
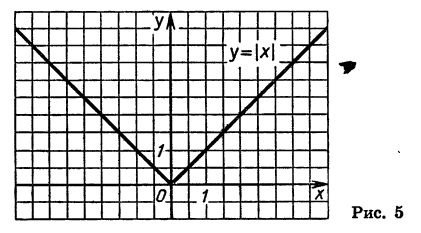
На рисунке 9 изображен график зависимости температуры воздуха р (в °С) от времени суток t (в часах). Мы видим, что в 2 ч и в 8 ч температура равнялась нулю, от 0 до 2 ч и от 8 до 24 ч она была выше нуля, а от 2 до 8 ч — ниже нуля. Из графика ясно также, что в течение первых пяти часов температура понижалась, затем в промежутке от 5 до 14 ч она повышалась, а потом опять понижалась.
С помощью графика мы выяснили некоторые свойства функции p=f(t), где t — время суток в часах, а р — температура воздуха в градусах Цельсия.
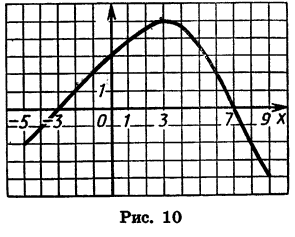
Рассмотрим теперь свойства функции y = f (х), график которой изображен на рисунке 10. Выясним сначала, при каких значениях х функция обращается в нуль, принимает положительные и отрицательные значения.
Найдем абсциссы точек пересечения графика с осью х. Получим х = — 3 и х = 7. Значит, функция принимает значение, равное нулю, при х = — 3 и х = 7. Значения аргумента, при которых функция обращается в нуль, называют нулями функции, т. е. числа -3 и 7 — нули рассматриваемой функции.
Нули функции разбивают ее область определения — промежуток [- 5; 9] на три промежутка: [-5; -3), (-3; 7) и (7; 9]. Для значений х из промежутка (-3; 7) точки графика расположены выше оси х, а для значений х из промежутков [- 5; — 3) и (7; 9] — ниже оси х. Значит, в промежутке ( — 3; 7) функция принимает положительные значения, а в каждом из промежутков [-5; -3) и (7; 9] — отрицательные.
Выясним теперь, как изменяются (увеличиваются или уменьшаются) значения данной функции с изменением х от — 5 до 9.
Из графика видно, что с увеличением х от -5 до 3 значения у увеличиваются, а с увеличением х от 3 до 9 значения у уменьшаются. Говорят, что в промежутке [-5; 3] функция y = f(x) является возрастающей, а в промежутке [3; 9] эта функция является убывающей.
Определение:
Функция называется возрастающей в некотором промежутке, если большему значению аргумента из этого промежутка соответствует большее значение функции;
функция называется убывающей в некотором промежутке, если большему значению аргумента из этого промежутка соответствует меньшее значение функции.
Иными словами, функцию y = f (х) называют возрастающей в некотором промежутке, если для любых 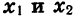

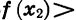
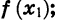
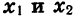

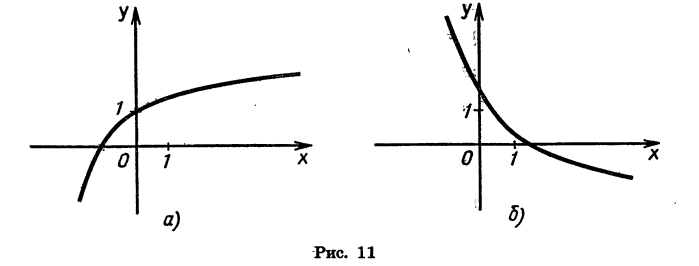
Если функция возрастает на всей области определения, то ее называют возрастающей функцией, а если убывает, то убывающей функцией. На рисунке 11 изображены графики возрастающей функции и убывающей функции.
Выясним, какими свойствами обладают некоторые изученные ранее функции.
Пример 1. Рассмотрим свойства функции 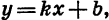
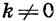
- Решив уравнение
найдем, что
Значит, у=0, при
- Выясним, при каких значениях х функция принимает положительные значения и при каких — отрицательные. Рассмотрим два случая:
Пусть 
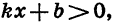
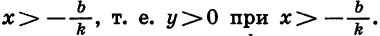
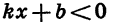
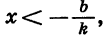
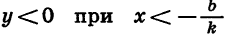
Пусть 
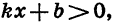
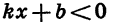
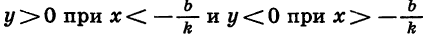
3. При 
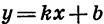

Докажем это. Пусть 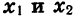

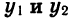
Рассмотрим разность
Множитель 

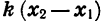
Если 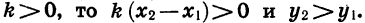

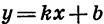
Если 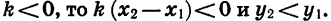
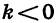
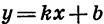
Пример:
Рассмотрим свойства функции 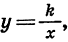
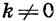
1.Так как дробь 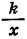
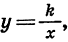
2. Если 
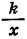
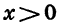
Если 
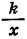
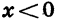
3. При 
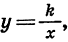
из промежутков 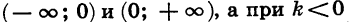
Доказательство этого свойства проводится аналогично тому, как это было сделано для линейной функции.
Заметим, что, хотя функция 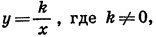
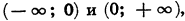
Видео:Алгебра 8 класс (Урок№6 - Решение уравнений графическим способом.)Скачать

Квадратный трехчлен
Квадратный трехчлен и его корни
Выражение 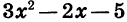
Определение:
Квадратным трехчленом называется многочлен вида 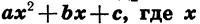
Значение квадратного трехчлена 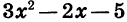
Мы видим, что при х = -1 квадратный трехчлен 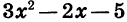
Корнем квадратного трехчлена называется значение переменной, при котором значение этого трехчлена равно нулю.
Для того чтобы найти корни квадратного трехчлена 

Пример:
Найдем корни квадратного трехчлена .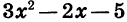
Значит, квадратный трехчлен 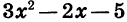
Так как квадратный трехчлен 

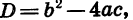
Преобразуем выражение в скобках. Для этого представим 12х в виде произведения 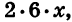
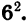
Рассмотрим задачу, при решении которой применяется выделение квадрата двучлена из квадратного трехчлена.
Пример:
Докажем, что из всех прямоугольников с периметром 20 см наибольшую площадь имеет квадрат.
Пусть одна сторона прямоугольника равна х см. Тогда другая сторона равна 10 — х см, а площадь прямоугольника равна
Раскрыв скобки в выражении х (10 — х), получим 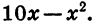
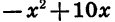
Так как выражение 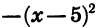
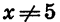
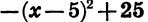
Разложение квадратного трехчлена на множители
Пусть требуется разложить на множители квадратный трехчлен 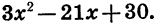
Для того чтобы разложить на множители трехчлен 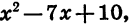
При х = 2 и х = 5 произведение 3 (х — 2) (х — 5), а следовательно, и трехчлен 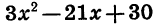
Мы представили квадратный трехчлен 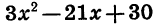
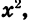
Такое разложение можно получить для любого квадратного трехчлена, имеющего корни. При этом считают, что если дискриминант квадратного трехчлена равен нулю, то этот трехчлен имеет два равных корня.
Теорема:
Если 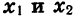

Вынесем за скобки в многочлене 
Так как корни квадратного трехчлена 

Заметим, что если квадратный трехчлен не имеет корней, то его нельзя разложить на множители, являющиеся многочленами первой степени.
Докажем это. Пусть трехчлен 
где 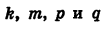
Произведение (kx+m) ( +q) обращается в нуль при
Следовательно, при этих значениях х обращается в нуль и трехчлен

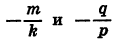
Пример:
Разложим на множители квадратный трехчлен
Решив уравнение 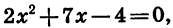
По теореме о разложении квадратного трехчлена на множители имеем:
Полученный результат можно записать иначе, умножив число 2 на двучлен 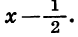
Пример:
Разложим на множители квадратный трехчлен
Решив уравнение 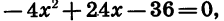
Пример:
Сократим дробь
Разложим на множители квадратный трехчлен 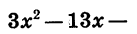
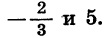
Квадратичная функция и ее график
Функция 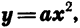
Одной из важных функций, которую мы будем рассматривать в дальнейшем, является квадратичная функция.
Определение:
Квадратичной функцией называется функция, которую можно задать формулой вида у = 
Примером квадратичной функции является зависимость пути от времени при равноускоренном движении. Если тело движется с ускорением 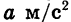
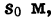
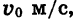
Если, например, а = 6, 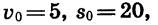
Изучение квадратичной функции мы начнем с частного случая — функции
При а = 1 формула 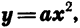
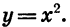
Построим график функции 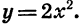
Построим точки, координаты которых указаны в таблице. Соединив их плавной линией, получим график функции 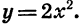
При любом 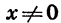
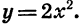


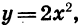

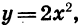

Построим теперь график функции 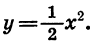
Построив точки, координаты которых указаны в таблице, и соединив их плавной линией, получим график функции 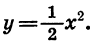
При любом 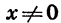
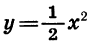


перейдет в точку графика функции 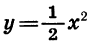

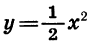

Вообще график функции 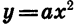

Рассмотрим теперь функцию 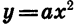
Воспользовавшись этой таблицей, построим график функции 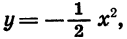
Сравним графики функций 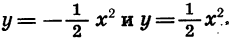
При любом х значения этих функций являются противоположными числами. Значит, соответствующие точки графиков симметричны относительно оси х. Иными словами, график функции
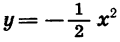
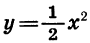
Вообще графики функций 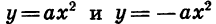
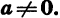
График функции 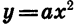
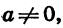

Сформулируем свойства функции 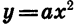
1.Если х = 0, то у = 0. График функции проходит через начало координат.
2. Если 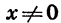
3. Противоположным значениям аргумента соответствуют равные значения функции. График функции симметричен относительно оси у.
4. Функция убывает в промежутке 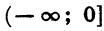
5. Наименьшее значение, равное нулю, функция принимает при х = 0, наибольшего значения функция не имеет. Областью значений функции является промежуток
Докажем свойство 4. Пусть 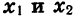
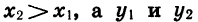
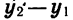
Так как 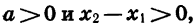
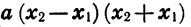
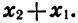
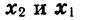
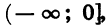
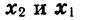
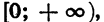
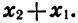
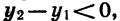

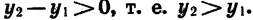
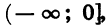
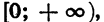
Теперь сформулируем свойства функции 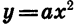
Из перечисленных свойств следует, что при а > 0 ветви параболы 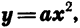
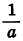
График функции 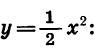
Чтобы получить таблицу значений функции 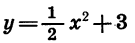
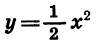
Построим точки, координаты которых указаны в таблице (2), и соединим их плавной линией. Получим график функции 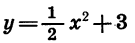
Легко понять, что каждой точке 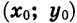
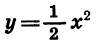
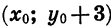
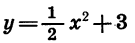
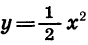
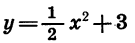
График функции 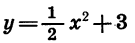
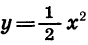
Вообще график функции 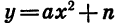
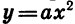
Пример:
Рассмотрим теперь функцию 
Для этого в одной системе координат построим графики функций
Для построения графика функции 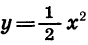


Построим график функции 
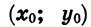
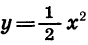
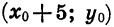

Значит, если переместить каждую точку графика функции 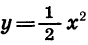

График функции 
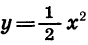
Вообще график функции 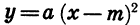
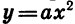
Вообще график функции 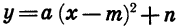
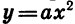
Рассмотрим квадратичную функцию у = 

Мы получили формулу вида 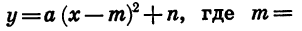
Значит, график функции 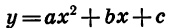
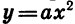
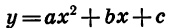
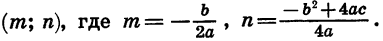
Приведем примеры построения графиков квадратичных функций.
Пример:
Построим график функции 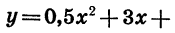
Графиком функции 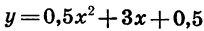
Значит, вершиной параболы является точка ( — 3; —4). Составим таблицу значений функции:
Построив точки, координаты которых указаны в таблице, и соединив их плавной линией, получим график функции 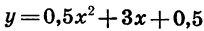
При составлении таблицы и построении графика учитывалось, что прямая х = — 3 является осью симметрии параболы. Поэтому мы брали точки с абсциссами — 4 и — 2, — 5 и — 1, — 6 и 0, симметричные относительно прямой х = — 3 (эти точки имеют одинаковые ординаты).
Пример:
Построим график функции 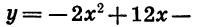
Графиком этой функции является парабола, ветви которой направлены вниз. Найдем координаты ее вершины:
Вычислив координаты еще нескольких точек, получим таблицу:
Соединив плавной линией точки, координаты которых указаны в таблице, получим график функции 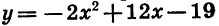
Пример:
Построим график функции
Графиком функции 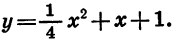
Вычислив координаты еще нескольких точек, получим таблицу:
График функции 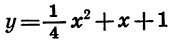
Видео:Графическое решение квадратных уравнений | Алгебра 8 класс #32 | ИнфоурокСкачать

Решение неравенств второй степени с одной переменной
Неравенства вида 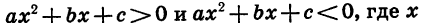
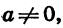
Решение неравенства второй степени с одной переменной можно рассматривать как нахождение промежутков, в которых соответствующая квадратичная функция принимает положительные или отрицательные значения.
Пример:
Решим неравенство
Рассмотрим функцию 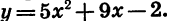
Выясним, как расположена эта парабола относительно оси х. Для этого решим уравнение
Значит, парабола пересекает ось х в двух точках, абсциссы которых равны
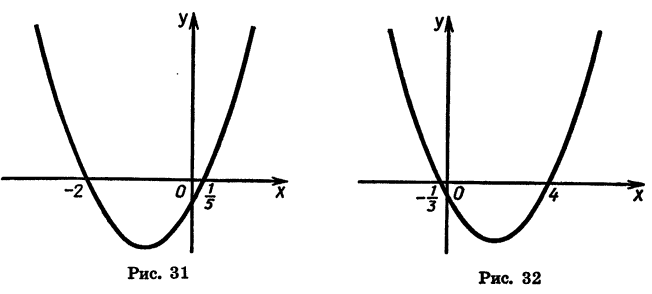
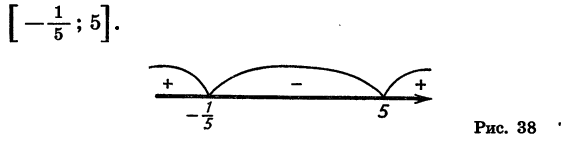
Покажем схематически, как расположена парабола в координатной плоскости (рис. 31). Из рисунка видно, что функция принимает отрицательные значения, когда
Следовательно, множеством решений неравенства 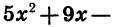
Покажем схематически, как расположена парабола в координатной плоскости (рис. 32). Из рисунка видно, что данное неравенство верно, если х принадлежит промежутку 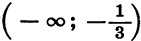
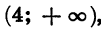
является объединение промежутков
Ответ можно записать так:
Пример:
Решим неравенство
Рассмотрим функцию 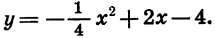
Выясним, как расположен график относительно оси х. Решим для этого уравнение 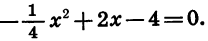
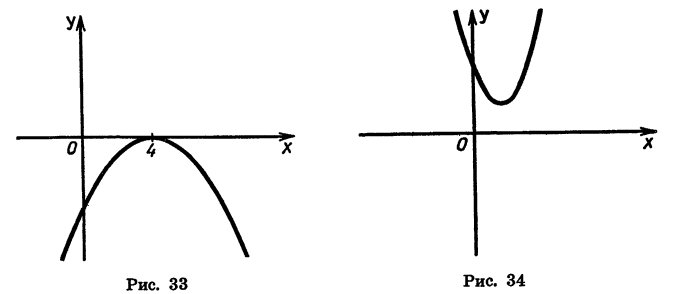
Изобразив схематически параболу (рис. 33), найдем, что функция принимает отрицательные значения при любом х, кроме 4.
Ответ можно записать так: х — любое число, не равное 4.
Пример:
Решим неравенство
График функции 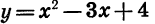
Чтобы выяснить, как расположена парабола относительно оси х, решим уравнение 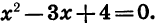
2) если трехчлен имеет корни, то отмечают их на оси х и через отмеченные точки проводят схематически параболу, ветви которой направлены вверх при а > 0 или вниз при а 0 или в нижней при а Решение неравенств методом интервалов
Областью определения этой функции является множество всех чисел. Нулями функции служат числа — 2, 3, 5. Они разбивают область определения функции на промежутки
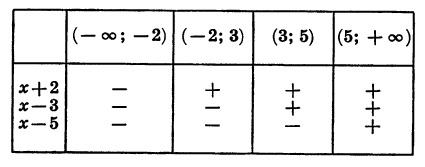
Выражение (х + 2) (х — 3) (х — 5) представляет собой произведение трех множителей. Знак каждого из этих множителей в рассматриваемых промежутках указан в таблице:
Отсюда ясно, что:
Мы видим, что в каждом из промежутков 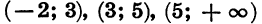
где х — переменная, а 

Это свойство используется для решения неравенств вида
где 
Пример:
Данное неравенство является неравенством вида (1), так как в левой части записано произведение 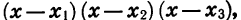
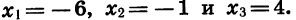
Отметим на координатной прямой нули функции
Найдем знаки этой функции в каждом из промежутков 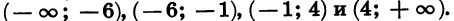
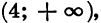
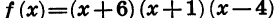
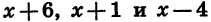
Из рисунка видно, что множеством решений неравенства является объединение промежутков
Ответ:
Рассмотренный способ решения неравенств называют методом интервалов.
Рассмотрим теперь примеры решения неравенств, которые сводятся к неравенствам вида (1).
Пример:
Решим неравенство
Приведем данное неравенство к виду (1). Для этого в двучлене 0,5 — х вынесем за скобку множитель -1. Получим:
Мы получили неравенство вида (1), равносильное данному.
Отметим на координатной прямой нули функции f (х) = х (х — 0,5)(х + 4) (рис. 37, а). Покажем знаком «плюс», что в крайнем справа промежутке функция принимает положительное значение, а затем, двигаясь справа налево, укажем знак функции в каждом из промежутков (рис. 37, б). Получим, что множеством решений неравенства является объединение промежутков
Ответ:
Пример:
Решим неравенство
Приведем неравенство к виду (1). Для этого в первом двучлене вынесем за скобки множитель 5, а во втором —1, получим:
Разделив обе части неравенства на -5, будем иметь:
Отметим на координатной прямой нули функции f(x) 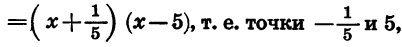
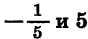
Ответ:
Заметим, что данное неравенство можно решить иначе, воспользовавшись свойствами графика квадратичной функции.
Пример:
Решим неравенство
Так как знак дроби 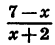
Приведя неравенство 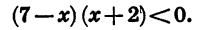
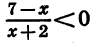
Ответ:
Видео:графический способ решения квадратного уравненияСкачать

Квадратичная функция и её построение
Парабола
Если х и у рассматривать как координаты точки, то уравнение (1) определит некоторое геометрическое место точек. Исследуем вид этого геометрического места. Заметим, что наше исследование будет неполным, так как останутся вопросы, которые нами пока не будут выяснены. Чем дальше мы будем продвигаться в изучении математики, тем полнее будут проводиться исследования.
1) Так как 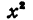
2) Так как и для —х и для х после возведения в квадрат получается одно и то же число, то точки, принадлежащие геометрическому месту и соответствующие значениям — х и х, имеют одну и ту же ординату и поэтому расположены симметрично относительно оси Оу (рис. 19).
3) Если х положительно, то, чем больше х, тем больше и 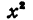
Геометрическое место, определяемое уравнением 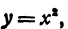
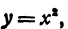
Теперь рассмотрим уравнение
Оно определяет геометрическое место точек. Сравнивая уравнения (1) и (2), замечаем, что при одном и том же х значения у отличаются только знаками, именно у, полученный из уравнения (2), всегда неположителен. Поэтому уравнение (2) тоже определяет параболу, вершина которой также находится в точке (0, 0), но ветви этой которой также находится в точке (0, 0), но ветви этой параболы идут от начала координат вниз вправо и вниз влево. График функции (2) изображен на рис. 21
Перейдем к рассмотрению уравнения
Сравним его с уравнением (1),
Если а положительно и больше единицы, то очевидно, что при одном и том же значении х величина у из уравнения (3) будет больше, чем величина у, взятая из уравнения (1). Отсюда можно заключить, что кривая, определяемая уравнением (3), отличается от параболы (1) только тем, что ординаты ее точек растянуты в а раз. Таким образом, кривая, определяемая уравнением (3), является более сжатой, чем парабола 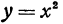
Если 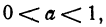
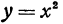
Теперь покажем, что кривая, определяемая уравнением
является параболой, только ее расположение относительно координатных осей другое, чем в разобранных случаях. Предварительно рассмотрим параллельный перенос осей координат.
Параллельный перенос осей координат
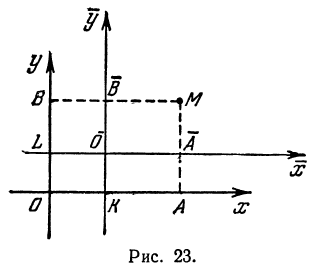
Пусть на плоскости дана система координат хОу (рис. 23). Рассмотрим новую систему координат 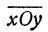
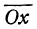
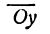
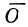
Обозначим координаты нового начала 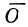
Возьмем произвольную точку М на плоскости; пусть ее координаты в старой системе будут х и у, а в новой 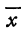
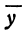
и (на основании формулы (2) из § 1 гл. I)
Переход от старой системы координат к указанной новой называется параллельным переносом или параллельным сдвигом осей координат. Приходим к выводу:
При параллельном сдвиге осей координат старая координата точки равна новой координате той же точки плюс координата нового начала в старой системе.
Исследование функции
Функция, определенная уравнением
называется квадратичной функцией. Функция 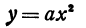
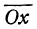
а ось 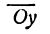
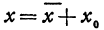
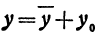
Разрешив это уравнение относительно 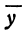
Координаты нового начала находятся в нашем распоряжении, поэтому их можно выбрать так, чтобы выполнялись условия
В этих уравнениях два неизвестных: х0 и у0. Найдем их:
Если взять новое начало в точке
то в уравнении (2) скобки
сделаются равными нулю, т. е. уравнение (2) примет вид
Полученное уравнение имеет вид, рассмотренный выше. Таким образом, уравнение 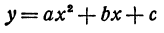
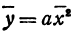
Уравнение 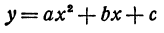
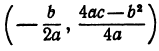
Переносим начало координат в точку (х0, у0), координаты которой пока неизвестны. Старые координаты я, у выражаются через новые 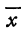
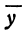
Подставляя эти выражения в уравнение (4), получим:
Выберем координаты нового начала так, чтобы соблюдались равенства
Решая полученную систему уравнений, будем иметь:
Следовательно, перенося начало координат в точку 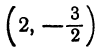
Следовательно, уравнение (4) определяет параболу, имеющу вершину в точке 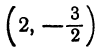
Приведем пример применения квадратичной функции в механике.
Задача:
Найти траекторию тела, брошенного под углом к горизонту. Угол бросания а, скорость бросания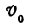
Решение:
Выберем оси координат так: ось Оу—вертикальная прямая, проведенная в точке бросания , ось Ох— горизонтальная прямая, начало координат—точка бросания (рис. 25).
Если бы не действовала сила притяжения Земли, то тело, брошенное под углом к горизонту, по инерции двигалось бы по прямой ОМ. За t сек оно прошло бы расстояние 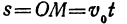
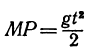
Найдем уравнение, связывающее х с у. Для этого из уравнения (*) найдем t и подставим это выражение в уравнение (**):
Мы получили уравнение траектории тела. Как мы видим, это есть квадратичная функция рассмотренного вида, следовательно, тело, брошенное под углом к горизонту, движется в безвоздушном пространстве по параболе, расположенной вершиной вверх, поскольку коэффициент при 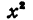
Какова наибольшая высота подъема тела над Землей? Чтобы ответить на этот вопрос, нужно найти вершину параболы. Как было выведено, вершина параболы имеет координаты
этому координаты вершины равны
Найдем теперь дальность полета тела, т. е. абсциссу точки падения. Для этого приравняем в уравнении (***) у нулю, получим уравнение
решая которое найдем два значения
первое из них дает точку бросания, а второе — искомую абсциссу точки падения.
Все эти рассуждения относятся к безвоздушному пространству; в воздухе и высота и дальность будут значительно меньше.
Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Видео:Графический способ решения систем уравнений. Алгебра, 9 классСкачать

Графическое решение квадратных уравнений
Разделы: Математика
На уроке учащиеся продемонстрировали знания и умения программы:
– распознавать виды функции, строить их графики;
– отрабатывали навыки построения квадратичной функции;
– отрабатывали графические способы решения квадратных уравнений, используя метод выделения полного квадрата.
Мне захотелось уделить особое внимание решению задач с параметром, так как ЕГЭ по математике предлагает очень много заданий такого типа.
Возможность применить на уроке такой вид работы дали мне сами ученики, так как они имеют достаточную базу знаний, которые можно углубить и расширить.
Заранее подготовленные учащимися шаблоны позволили экономить время урока. В ходе урока мне удалось реализовать поставленные задачи в начале урока и получить ожидаемый результат.
Использование физкультминутки помогло избежать переутомления учащихся, сохранить продуктивную мотивацию получения знаний.
В целом результатом урока я довольна, но думаю, что есть еще резервные возможности: современные инновационные технологические средства, которыми мы, к сожалению, не имеем возможности пользоваться.
Тип урока: закрепление изученного материала.
Цели урока:
- Общеобразовательные и дидактические:
- развивать разнообразные способы мыслительной деятельности учащихся;
- формировать способности самостоятельного решения задач;
- воспитывать математическую культуру учащихся;
- развивать интуицию учащихся и умение пользоваться полученными знаниями.
- Учебные цели:
- обобщить ранее изученные сведения по теме «Графическое решение квадратных уравнений»;
- повторить построение графиков квадратичной функции;
- сформировать навыки использования алгоритмов решения квадратичных уравнений графическим методом.
- Воспитательные:
- привитие интереса к учебной деятельности, к предмету математики;
- формирование толерантности (терпимости), умения работать в коллективе.
I. Организационный момент
– Сегодня на уроке мы обобщим и закрепим графическое решение квадратных уравнений различными способами.
В дальнейшем эти навыки нам будут нужны в старших классах на уроках математики при решении тригонометрических и логарифмических уравнений, нахождения площади криволинейной трапеции, а также на уроках физики.
II. Проверка домашней работы
Разберем на доске № 23.5(г).
Решить это уравнение с помощью параболы и прямой.
х 2 + х – 6 = 0
Преобразуем уравнение: х 2 = 6 – х
Введем функции:
у = х 2 ; квадратичная функция у = 6 – х линейная,
графиком явл. парабола, графиком явл. прямая,
Строем в одной системе координат графики функций (по шаблону)
Получили две точки пересечения.
Решением квадратного уравнения являются абсциссы этих точек х1 = – 3, х2 = 2.
III. Фронтальный опрос
- Что является графиком квадратичной функции?
- Скажите алгоритм построения графика квадратичной функции?
- Что называется квадратичным уравнением?
- Приведите примеры квадратичных уравнений?
- Запишите на доске свой пример квадратичного уравнения, Назовите, чему равны коэффициенты?
- Что значит решить уравнение?
- Сколько способов вы знаете графического решения квадратных уравнений?
- В чем заключается графические способы решение квадратных уравнений:
IV. Закрепление материала
На доске решают учащиеся первым, вторым, третьим способами.
Класс решает четвертым

– х 2 + 6х – 5 = – (х 2 – 6х + 5) = – (х 2 – 6х + 32 – 9 + 5) = – ((х – 3) 2 – 4) = – (х – 3) 2 + 4
Получили квадратное уравнение:
у = – (х 2 – 3) 2 + 4
Квадратичная функция вида у = а (х + L) 2 + m
Графиком явл. парабола, ветви направлены вниз, сдвиг основной параболы по оси Ох в право на 3 ед., по оси Оу вверх на 4 ед., вершина (3; 4).
Строим по шаблону.
Нашли точки пересечения параболы с осью Ох. Абсциссы этих точек явл. решением данного уравнения. х = 1, х = 5.
Давайте посмотрим другие графические решение у доски. Прокомментируйте свой способ решения квадратных уравнений.
1 ученик

Введем функцию у = – х + 6х – 5, квадратичная функция, графиком является парабола, ветви направлены вниз, вершина
х0 = – в/2а
х0 = – 6/– 2 = 3
у0 = – 3 2 + 18 = 9; точка (3; 9)
ось симметрии х = 3
Строим по шаблону
Получили точки пересечения с осью Ох, абсциссы этих точек являются решением квадратного уравнения. Два корня х1 = 1, х2 = 5
2 ученик
Преобразуем: – х 2 + 6х = 5

х0 = – 6/– 2 = 3
у0 = – 3 2 + 18 = 9;
(3; 9).
ось симметрии х = 3
Строим по шаблону
Получили точки пересечения
параболы и прямой, их абсциссы являются решением квадратного уравнения. Два корня х1 = 1, х2 = 5
Итак, одно и тоже уравнение можно решать различными способами, а ответ получаться должен один и тот же.
V. Физкультминутка
VI. Решение задачи с параметром
При каких значениях р уравнение х 2 + 6х + 8 = р:
– Не имеет корней?
– Имеет один корень?
– Имеет два корня?
Чем отличается это уравнение от предыдущего?
Правильно, буквой!
Эту букву в дальнейшем мы будем называть параметром, Р.
Пока она вам ни о чем не говорит. Но мы будем в дальнейшем решать различные задачи с параметром.
Сегодня решим квадратное уравнение с параметром графическим методом, используя третий способ с помощью параболы и прямой параллельной оси абсцисс.
Ученик помогает учителю решать у доски.
С чего начнем решать?

у1 = х 2 + 6х + 8 у2 = р линейная функция,
квадратичная функция, графиком является прямая
графиком явл. парабола,
ветви направлены вниз, вершина
Ось симметрии х = 3, таблицу строить не буду, а возьму шаблон у = х 2 и приложу к вершине параболы.
Парабола построена! Теперь надо провести прямую у = р.
– Где надо начертить прямую р, чтобы получить два корня?
– Где надо начертить прямую р, чтобы получить один корень?
– Где надо начертить прямую р, чтобы не было корней?
– Итак, сколько наше уравнение может иметь корней?
– Понравилась задача? Спасибо за помощь! Оценка 5.
VII. Самостоятельная работа по вариантам (5 мин.)
у = х 2 – 5х + 6 у = – х 2 + х – 6
Решить квадратное уравнение графическим способом, выбирая для вас удобный способ. Если кто-то справится с заданием раньше, проверьте свое решение другим способом. За это будет выставляться дополнительная оценка.
VIII. Итог урока
– Чему научились вы на сегодняшнем уроке?
– Сегодня на уроке мы с вами квадратные уравнения решали графическим методом, используя различные способы решения, и рассмотрели графический способ решения квадратного уравнения с параметром!
– Переходим к домашнему заданию.
IХ. Домашнее задание
1. Домашняя контрольная работа на стр. 147, из задачника Мордковича по вариантам I и II.
2. На кружке, в среду, будем решать V-м способом, (гипербола и прямая).
Х. Литература:
1. А.Г. Мордкович. Алгебра-8. Часть 1. Учебник для учащихся образовательных учреждений. М.: Мнемозина, 2008 г.
2. А.Г. Мордкович, Л.А.Александрова, Т.Н. Мишустина, Е.Е. Тульчинская. Алгебра – 8. Часть 2. Задачник для учащихся образовательных учреждений. М.: Мнемозина, 2008 г.
3. А.Г. Мордкович. Алгебра 7-9. Методическое пособие для учителя.М.: Мнемозина, 2004 г.
4. Л.А. Александрова. Алгебра-8. Самостоятельные работы для учащихся образовательных учреждений./Под ред. А.Г. Мордковича. М.: Мнемозина, 2009 г.
Видео:Решение квадратных неравенств | МатематикаСкачать

Презентация по математике «Графическое решение квадратных уравнений» (8 класс)
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Описание презентации по отдельным слайдам:
3х2 + 6х = 0 2) х2–4 = 0 3) (х–5)(х+1) = 0 4) х2–4х+3 = 0.
3х2 + 6х = 0 3х (х+2) = 0 х = 0 или х+2 = 0 х = – 2 Ответ: – 2; 0. х2 – 4 = 0 (х – 2 ) (х + 2) = 0 х – 2 = 0 или х + 2 = 0 х = 2 х = –2 Ответ: –2; 2.
(х–5)(х+1) = 0 (х2 – 4х –5 = 0) х – 5 = 0 или х+1 = 0 Х = 5 х = –1 Ответ: –1; 5. х2–4х+3 = 0 Как его решить?
Квадратным уравнением называют уравнение вида ах2+bх+с=0, где а, b, с – любые числа, причем а 0.
1. Построить график квадратичной функции у = ах2 + bх + с. 2. Найти точки пересечения параболы с осью х. 3. Записать корни уравнения, которыми являются абсциссы точек пересечения
1 способ Корнями уравнения являются абсциссы точек пересечения с осью х. Ответ: х1 = -1, х2 = 3. -1 3 1 Построим график функции у = х2 — 2х – 3. График – парабола, ветви вверх. Вершина (х0; у0): х 0 = — , а = 1, b = — 2, х0 = — = 1. у0 = 12 – 2 ∙ 1 – 3 = — 4, 2. Симметричные точки: х = 0 и х = 2, у (0) = у (2) = 02 — 2∙ 0 – 3 = — 3 , (0; — 3), (2; — 3) 3. Дополнительные точки: х = — 1 и х = 3, у (- 1) = у (3) = 1 + 2 – 3 = 0, (- 1; 0), (3; 0) (1; — 4) х у
Преобразуем уравнение к виду Построим в одной системе координат графики функций -это парабола -это прямая 3 -1 3 Корнями уравнения являются абсциссы точек пересечения: -1 и 3 Ответ: х1 = -1, х2 = 3. 2 способ х у 9
6 -1 3 х у 3 способ Преобразуем уравнение х2 — 2х – 3 = 0 к виду х2 — 3 = 2х — 3 Построим в одной системе координат графики функций у = х2 – 3 и у = 2х у = х2 — 3 – это парабола у = 2х – это прямая Корнями уравнения являются абсциссы точек пересечения: -1 и 3 Ответ: х1 = -1, х2 = 3.
4 способ у = х — 2 – это прямая у = – это гипербола Преобразуем уравнение х2 — 2х – 3 = 0 к виду х — 2 = Построим в одной системе координат графики функций у = х – 2 и у = Корнями уравнения являются абсциссы точек пересечения: -1 и 3 Ответ: х1 = -1, х2 = 3. 3
5 способ Преобразуем уравнение х2 — 2х – 3 = 0 к виду (х — 1)2 = 4 Построим в одной системе координат графики функций у = (х – 1)2 и у = 4 у = (х — 1)2 — сдвиг параболы вправо на 1 единицу у = 4 — это прямая -1 4 3 х у Корнями уравнения являются абсциссы точек пересечения: -1 и 3 Ответ: х1 = -1, х2 = 3.
1 способ 2 способ 3 способ 4 способ 5 способ х2 — 3 = 2х х — 2 = (х — 1)2 = 4
х2 — х – 3 = 0 Решим вторым способом х2 = х + 3 у = х2 – парабола у = х + 3 – прямая у х 1 А В
Немного истории В 1591г. Франсуа Виет вывел формулы для нахождения корней квадратных уравнений, однако он не признавал отрицательных чисел. Лишь в XVIII веке благодаря трудам учёных Жирара, Декарта, Ньютона, способ решения квадратных уравнений принял современный вид.
1 способ 2 способ 3 способ 4 способ 5 способ Ответ: х = -2, х = 4. х2 – 2х – 8 = 0
Тема сложная, вызывает у меня затруднение – Есть отдельные затруднения – Мне всё понятно –
Краткое описание документа:
Данная презентация создана для урока алгебры в 8 классе по теме » Графическое решение квадратных уравнений» по учебнику А.М. Мордковича. На уроке применяется технология разноуровневой дифференциации для обучающихся трёх гомогенных групп и проблемная ситуация. Одна и та же задача решается несколькими способами с помощью потроения графиков функций, которые изучались на данный момент. В ходе урока используется историческая справка о решении квадратных уравнений. Данная презентация помогает быстро и наглядно провести проверку выполнения дифференцированных заданий, которые выполняют группы.
Курс повышения квалификации
Охрана труда
- Сейчас обучается 112 человек из 42 регионов
Курс профессиональной переподготовки
Библиотечно-библиографические и информационные знания в педагогическом процессе
- Сейчас обучается 350 человек из 63 регионов
Курс профессиональной переподготовки
Охрана труда
- Сейчас обучается 231 человек из 54 регионов
Ищем педагогов в команду «Инфоурок»
Видео:Решение системы линейных уравнений графическим методом. 7 класс.Скачать

Дистанционные курсы для педагогов
Самые массовые международные дистанционные
Школьные Инфоконкурсы 2022
33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
5 574 158 материалов в базе
Другие материалы
- 15.03.2015
- 1013
- 0
- 15.03.2015
- 816
- 2
- 15.03.2015
- 1517
- 1
- 15.03.2015
- 1195
- 0
- 15.03.2015
- 2498
- 0
- 15.03.2015
- 505
- 0
- 15.03.2015
- 582
- 0
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Добавить в избранное
- 15.03.2015 3250
- PPTX 815.5 кбайт
- 240 скачиваний
- Оцените материал:
Настоящий материал опубликован пользователем Касаткина Светлана Михайловна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Автор материала
- На сайте: 6 лет и 11 месяцев
- Подписчики: 0
- Всего просмотров: 4286
- Всего материалов: 2
Московский институт профессиональной
переподготовки и повышения
квалификации педагогов
Видео:5 способов решения квадратного уравнения ➜ Как решать квадратные уравнения?Скачать

Дистанционные курсы
для педагогов
663 курса от 690 рублей
Выбрать курс со скидкой
Выдаём документы
установленного образца!
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
В Воронеже продлили удаленное обучение для учеников 5-11-х классов
Время чтения: 1 минута
Приемная кампания в вузах начнется 20 июня
Время чтения: 1 минута
Объявлен конкурс дизайн-проектов для школьных пространств
Время чтения: 2 минуты
В Курганской области дистанционный режим для школьников продлили до конца февраля
Время чтения: 1 минута
Онлайн-конференция о создании школьных служб примирения
Время чтения: 3 минуты
Минпросвещения подключит студотряды к обновлению школьной инфраструктуры
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
📸 Видео
Как решать уравнение графически. 3 способа графического решения квадратного уравнения.Скачать

Графический метод решения уравнений 8 классСкачать

Квадратное уравнение. 1 урок.Скачать

Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Квадратные уравнения и геометрическая алгебра древнихСкачать

Решаем квадратные уравнения аналитическим и графическим способамиСкачать

Решение биквадратных уравнений. 8 класс.Скачать

Решение системы уравнений графическим методомСкачать

Решение квадратных неравенств графическим методом, если дискриминант равен нулю. 8 класс.Скачать


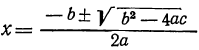
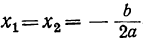
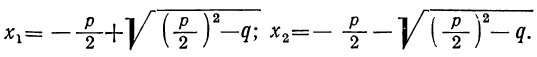
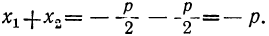
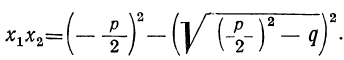
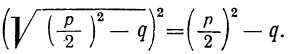
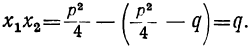
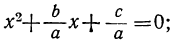
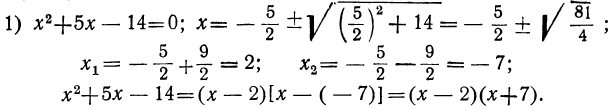
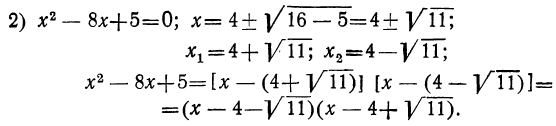
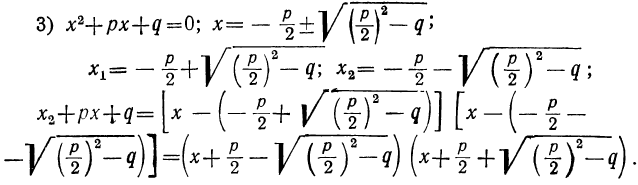
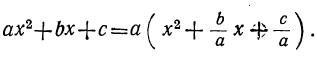
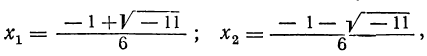
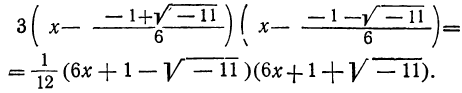
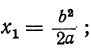
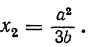
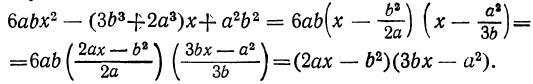
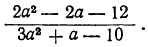
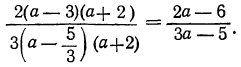
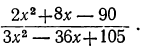
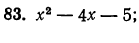
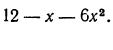
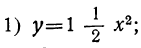
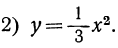
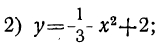
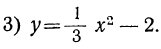
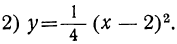
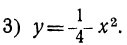
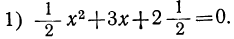
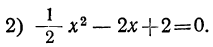
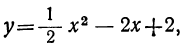
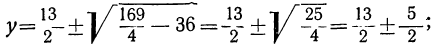
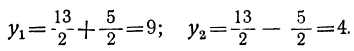
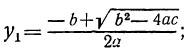
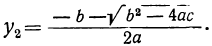
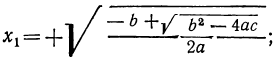
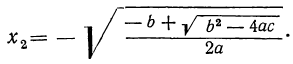
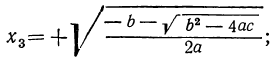
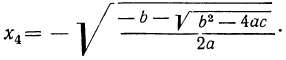
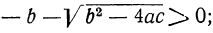
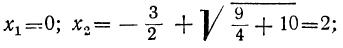
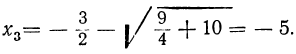
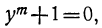
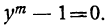
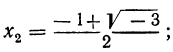
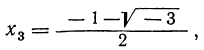
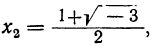
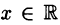
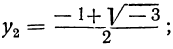
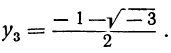
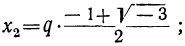
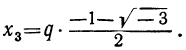
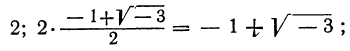
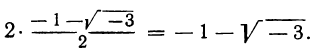
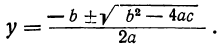
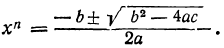
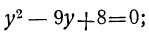
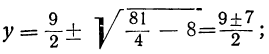
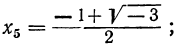
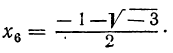
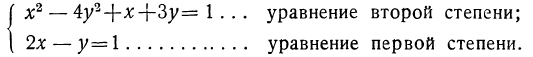
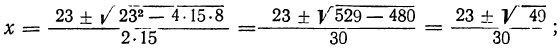
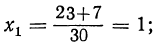
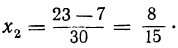
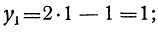
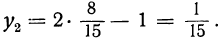
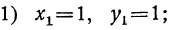
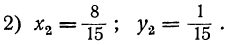
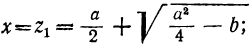
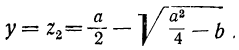
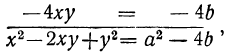
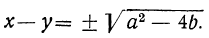
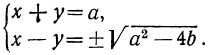
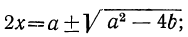
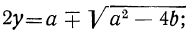
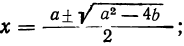
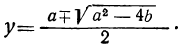
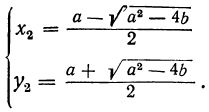
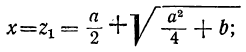
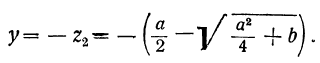
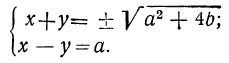
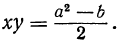
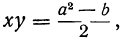
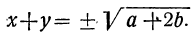
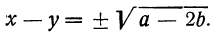
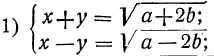
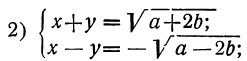
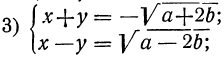
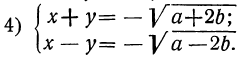
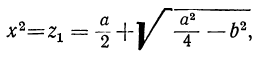
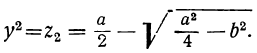
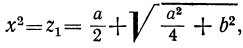
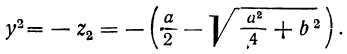
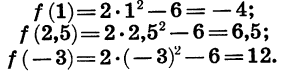
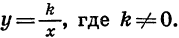
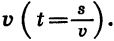
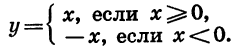
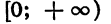

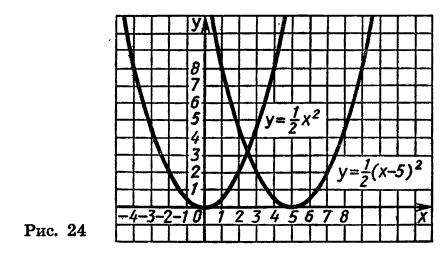
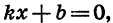 найдем, что
найдем, что 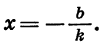 Значит, у=0, при
Значит, у=0, при