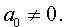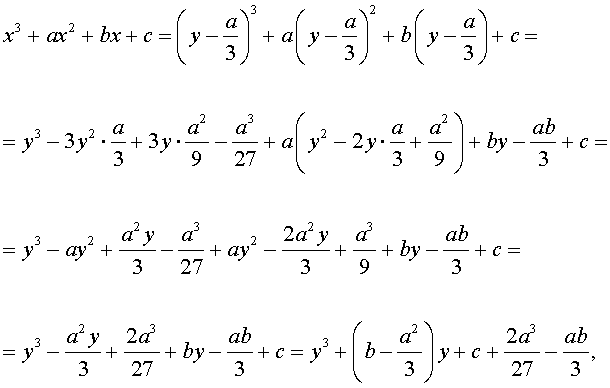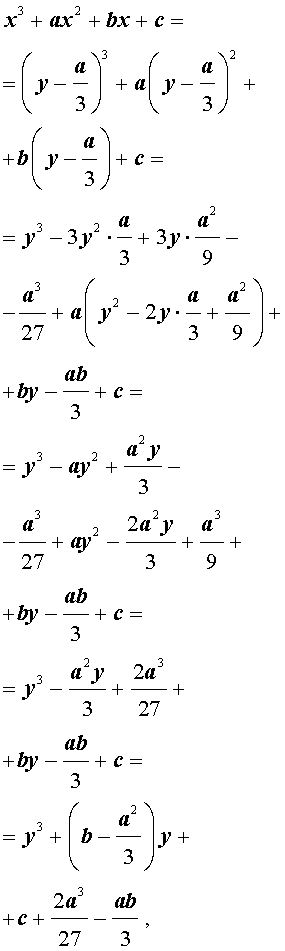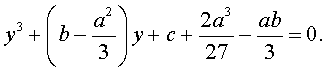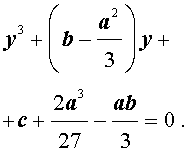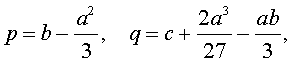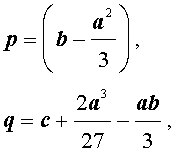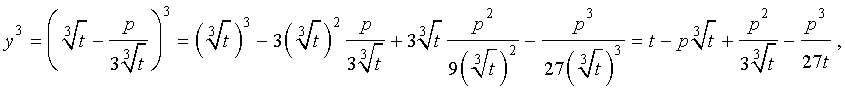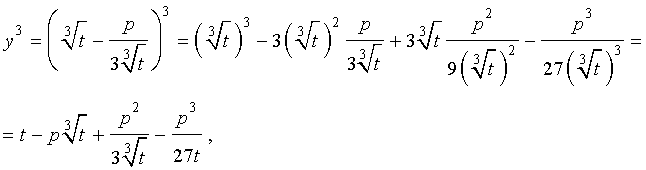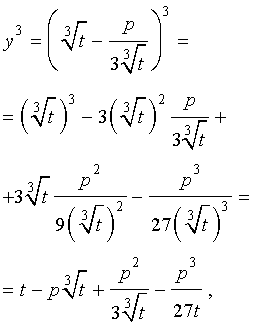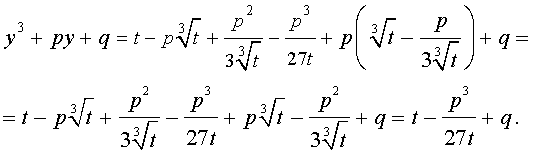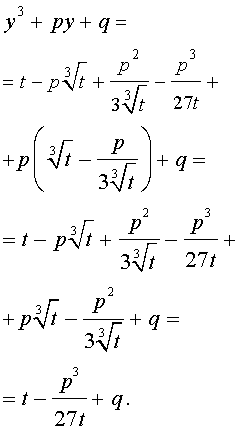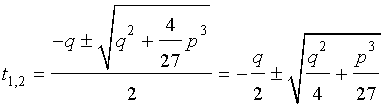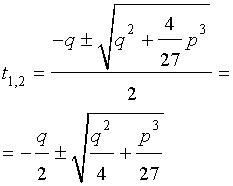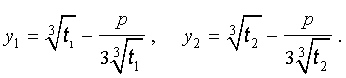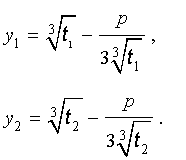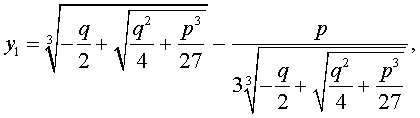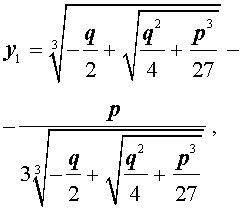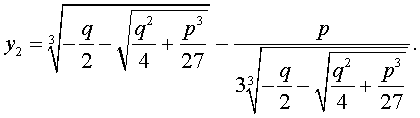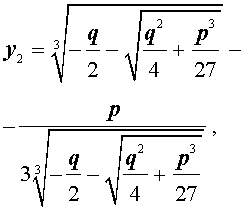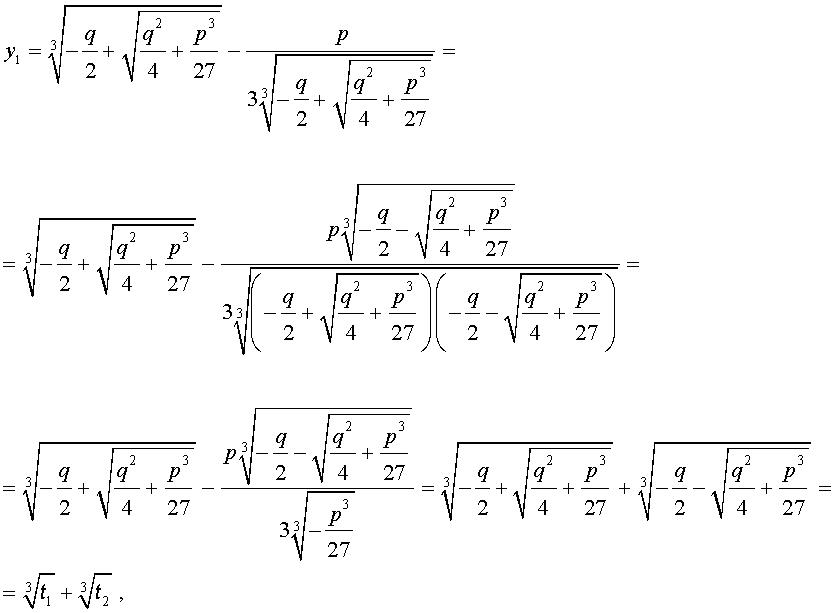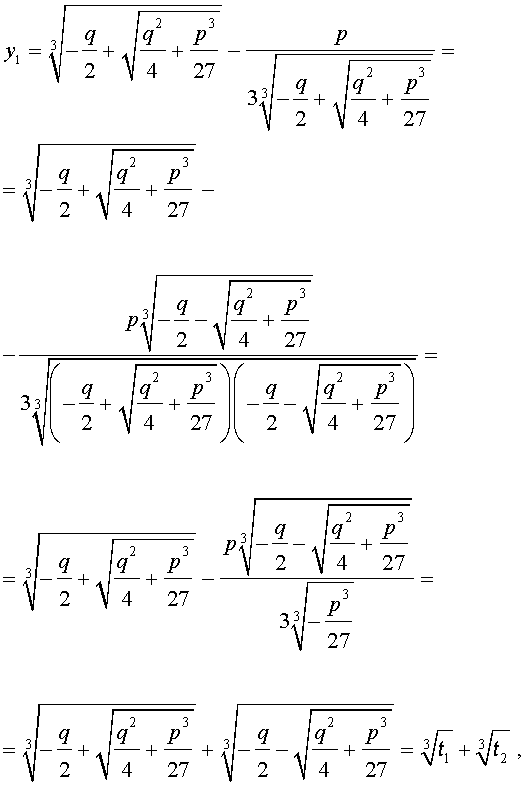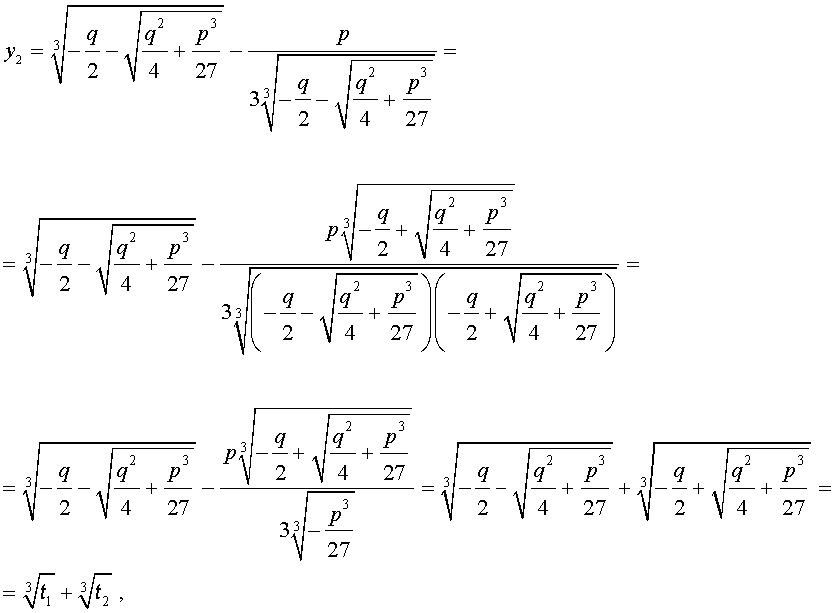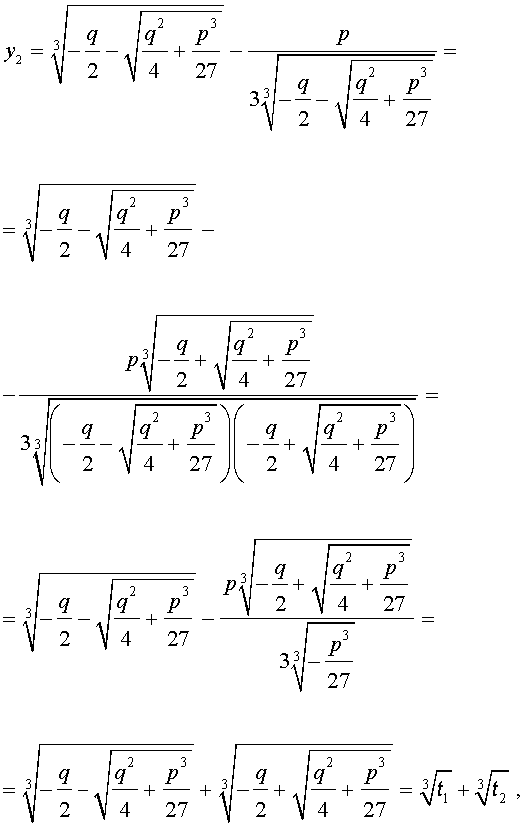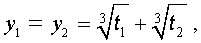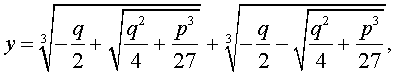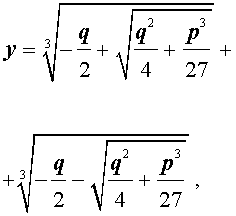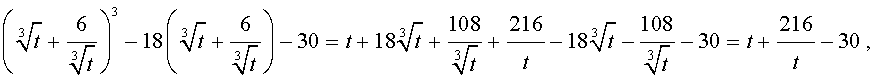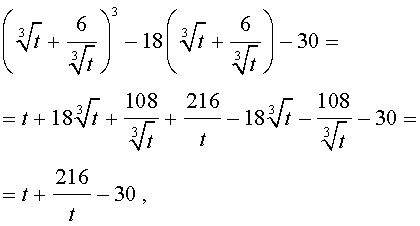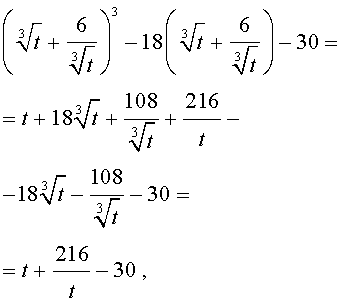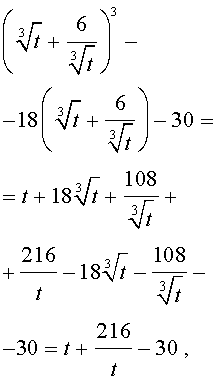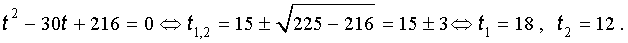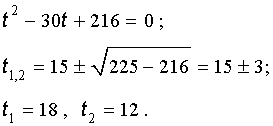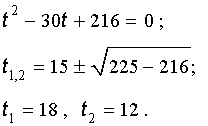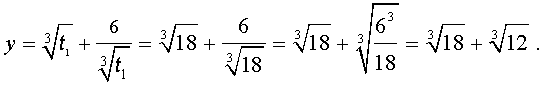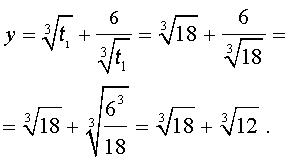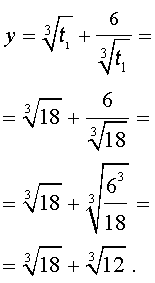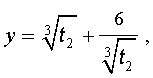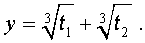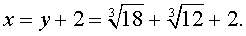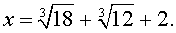Решение кубических уравнений методом замены

Схема метода Кардано

Приведение кубических уравнений к трехчленному виду

Сведение трёхчленных кубических уравнений к квадратным уравнениям при помощи метода Никколо Тартальи

Формула Кардано

Пример решения кубического уравнения

Видео:КАК РЕШАТЬ КУБИЧЕСКИЕ УРАВНЕНИЯ | Разбираем на конкретном примереСкачать

Схема метода Кардано

Целью данного раздела является вывод формулы Кардано для решения уравнений третьей степени ( кубических уравнений )

где a₀, a₁, a₂, a₃ – произвольные вещественные числа,

Вывод формулы Кардано состоит из двух этапов.

На первом этапе кубические уравнения вида (1) приводятся к кубическим уравнениям, у которых отсутствует член со второй степенью неизвестного. Такие кубические уравнения называют трёхчленными кубическими уравнениями .

На втором этапе трёхчленные кубические уравнения решаются при помощи сведения их к квадратным уравнениям.

Видео:✓ Как решать кубические уравнения. Формула Кардано | Ботай со мной #025 | Борис ТрушинСкачать

Приведение кубических уравнений к трехчленному виду

Разделим уравнение (1) на старший коэффициент a₀ . Тогда оно примет вид

где a, b, c – произвольные вещественные числа.

Заменим в уравнении (2) переменную x на новую переменную y по формуле:

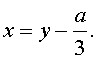(3)

то уравнение (2) примет вид

В результате уравнение (2) примет вид

Если ввести обозначения

то уравнение (4) примет вид

где p, q – вещественные числа.

Уравнения вида (5) и являются трёхчленными кубическими уравнениями , у которых отсутствует член со второй степенью неизвестного.

Первый этап вывода формулы Кардано завершён.

Видео:Математика | Кубические уравнения по методу СталлонеСкачать

Сведение трёхчленных кубических уравнений к квадратным уравнениям при помощи метода Никколо Тартальи

Следуя методу, примененому Никколо Тартальей (1499-1557) для решения трехчленных кубических уравнений, будем искать решение уравнения (5) в виде

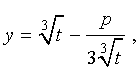(6)

где t – новая переменная.

то выполнено равенство:

Следовательно, уравнение (5) переписывается в виде

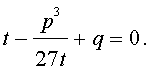(7)

Если теперь уравнение (7) умножить на t , то мы получим квадратное уравнение относительно t :

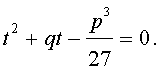(8)

Видео:КУБИЧЕСКИЕ УРАВНЕНИЯ 😉 #егэ #математика #профильныйегэ #shorts #огэСкачать

Формула Кардано

Решение уравнения (8) имеет вид:

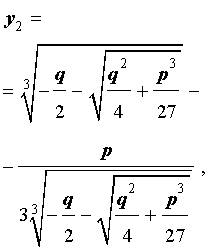
В соответствии с (6), отсюда вытекает, что уравнение (5) имеет два решения:

В развернутой форме эти решения записываются так:

Покажем, что, несмотря на кажущиеся различия, решения (10) и (11) совпадают.

С другой стороны,

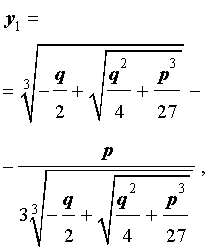
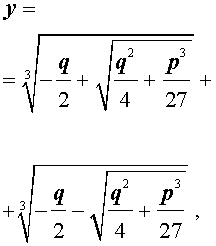
и для решения уравнения (5) мы получили формулу

которая и называется «Формула Кардано» .

Замечание . Поскольку у каждого комплексного числа, отличного от нуля, существуют три различных кубических корня, то, для того, чтобы избежать ошибок при решении кубических уравнений в области комплексных чисел, рекомендуется использовать формулу Кардано в виде (10) или (11).

Видео:Кубические уравнения. Деление столбиком. Схема Горнера.Скачать

Пример решения кубического уравнения

Пример . Решить уравнение

Решение . Сначала приведем уравнение (13) к трехчленному виду. Для этого в соответствии с формулой (3) сделаем в уравнении (13) замену

Следовательно, уравнение (13) принимает вид

Теперь в соответствии с формулой (6) сделаем в уравнении (15) еще одну замену

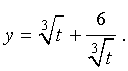(16)

то уравнение (15) примет вид

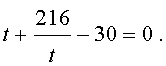(17)

Далее из (17) получаем:

Отсюда по формуле (16) получаем:

Заметим, что такое же, как и в формуле (18), значение получилось бы, если бы мы использовали формулу

или использовали формулу

Далее из равенства (18) в соответствии с (14) получаем:

Таким образом, мы нашли у уравнения (13) вещественный корень

Замечание 1 . У уравнения (13) других вещественных корней нет.

Замечание 2 . Поскольку произвольное кубическое уравнение в комплексной области имеет 3 корня с учетом кратностей, то до полного решения уравнения (13) остается найти еще 2 корня. Эти корни можно найти разными способами, в частности, применив вариант формулы Кардано для области комплексных чисел. Однако применение такого варианта формулы Кардано значительно выходит за рамки курса математики даже специализированных математических школ.

Видео:ОГЭ №21 Как решать кубическое уравнение x^3+4x^2-9x-36=0 Группировка Деление многочлена столбикомСкачать

«Решение уравнений высших степеней». 9-й класс

Разделы: Математика

Класс: 9

Учебная:

Развивающая:

1. Развитие внимания учащихся.
2. Развитие умения добиваться результатов труда.
3. Развитие интереса к изучению алгебры и навыков самостоятельной работы.

Воспитывающая:

Оборудование: компьютер, проектор.

1 этап работы. Организационный момент.

2 этап работы. Мотивация и выход на постановку проблемы

Уравнение одно из важнейших понятий математики. Развитие методов решения уравнений, начиная с зарождения математики как науки, долгое время было основным предметом изучения алгебры.

В школьном курсе изучения математики очень много внимания уделяется решению различного вида уравнений. До девятого класса мы умели решать только линейные и квадратные уравнения. Уравнения третьей, четвёртой и т.д. степеней называются уравнениями высших степеней. В девятом классе мы познакомились с двумя основными приёмами решения некоторых уравнений третьей и четвёртой степеней: разложение многочлена на множители и использование замены переменной.

А можно ли решить уравнения более высоких степеней? На этот вопрос мы постараемся сегодня найти ответ.

3 этап работы. Повторить ранее изученный материал. Ввести понятие уравнения высших степеней.

1) Решение линейного уравнения.

Линейным называется уравнение вида , где по определению. Такое уравнение имеет единственный корень .

2) Решение квадратного уравнения.

Квадратным называется уравнение вида , где . Количество корней и сами корни определяются дискриминантом уравнения . Для уравнение корней не имеет, для имеет один корень (два одинаковых корня)

, для имеет два различных корня .

Из рассмотренных линейных и квадратных уравнений видим, что количество корней уравнения не более его степени. В курсе высшей алгебры доказывается, что уравнение -й степени имеет не более n корней. Что касается самих корней, то тут ситуация намного сложнее. Для уравнений третьей и четвёртой степеней известны формулы для нахождения корней. Однако эти формулы очень сложны и громоздки и практического применения не имеют. Для уравнений пятой и более высоких степеней общих формул не существует и существовать не может (как было доказано в XIX в. Н. Абелем и Э. Галуа).

Будем называть уравнения третьей, четвёртой и т.д. степеней уравнениями высших степеней. Некоторые уравнения высоких степеней удаётся решить с помощью двух основных приёмов: разложением многочлена на множители или с использованием замены переменной.

3) Решение кубического уравнения.

Решим кубическое уравнение

Сгруппируем члены многочлена, стоящего в левой части уравнения, и разложим на множители. Получим:

Произведение множителей равно нулю, если один из множителей равен нулю. Получаем три линейных уравнения:

Итак, данное кубическое уравнение имеет три корня: ; ;.

4) Решение биквадратного уравнения.

Очень распространены биквадратные уравнения, которые имеют вид (т.е. уравнения, квадратные относительно ). Для их решения вводят новую переменную .

Решим биквадратное уравнение .

Введём новую переменную и получим квадратное уравнение , корнями которого являются числа и 4.

Вернёмся к старой переменной и получим два простейших квадратных уравнения:

(корни и )

(корни и )

Итак, данное биквадратное уравнение имеет четыре корня:

; ;.

Попробуем решить уравнение используя выше изложенные приёмы.

4 этап работы. Привести некоторые утверждения о корнях многочлена вида , где многочлен n-й степени

Приведём некоторые утверждения о корнях многочлена вида :

1) Многочлен -й степени имеет не более корней (с учётом их кратностей). Например, многочлен третьей степени не может иметь четыре корня.

2) Многочлен нечётной степени имеет хотя бы один корень. Например, многочлены первой, третьей, пятой и т.д. степени имеют хотя бы один корень. Многочлены чётной степени корней могут и не иметь.

3) Если на концах отрезка значения многочлена имеют разные знаки (т.е. ,), то на интервале находится хотя бы один корень. Это утверждение широко используется для приближенного вычисления корней многочлена.

4) Если число является корнем многочлена вида , то этот многочлен можно представить в виде произведения , где многочлен (-й степени. Другими словами, многочлена вида можно разделить без остатка на двучлен . Это позволяет уравнение -й степени сводить к уравнению (-й степени (понижать степень уравнения).

5) Если уравнение со всеми целыми коэффициентами (причём свободный член ) имеет целый корень , то этот корень является делителем свободного члена . Такое утверждение позволяет подобрать целый корень многочлена (если он есть).

5 этап работы. Показать как применяется теория делимости для решения уравнений высших степеней. Рассмотреть примеры решения уравнений высших степеней , в которых для разложения левой части на множители используется способ деления многочлена на многочлен “уголком”.

Пример 1. Решим уравнение .

Если это уравнение имеет целый корень, то он является делителем свободного члена (-1), т.е. равняется одному из чисел: . Проверка показывает, что корнем уравнения является число -1. Значит, многочлен можно представить в виде произведения , т.е. многочлен можно без остатка разделить на двучлен . Выполним такое деление “уголком”:

Таким образом, мы фактически разложили левую часть уравнения на множители:

Произведение множителей равно нулю, если один из множителей равен нулю. Получаем два уравнения:

Итак, данное уравнение имеет три корня:

Пример 2. Решим уравнение .

Если это уравнение имеет целый корень, то он является делителем свободного члена (9),т.е. равняется одному из чисел: ;. Проверим:

Значит, многочлен можно представить в виде произведения , т.е. многочлен можно без остатка разделить на двучлен . Выполним такое деление “уголком”:

Таким образом, мы разложили левую часть уравнения на множители:

Аналогичным образом поступим и с многочленом .

Если это уравнение имеет целый корень, то он является делителем свободного члена (9), т.е. равняется одному из чисел: ;. Проверим:

Значит, многочлен можно представить в виде

произведения , т.е. многочлен можно без остатка разделить на двучлен . Выполним такое деление “уголком”:

Таким образом, мы разложили левую часть исходного уравнения на множители:

Произведение множителей равно нулю, если один из множителей равен нулю. Получаем три уравнения:

Итак, данное уравнение имеет четыре корня:

6 этап работы. Закрепление изученного материала.

Решите уравнения высших степеней, используя способ деления многочлена на многочлен “уголком”.

7 этап работы. Вывод урока.

Решить уравнения высших степеней можно следующим образом:

• используя формулы для нахождения корней (если они известны);
• используя замену переменной;
• раскладывая многочлен в левой части уравнения на множители, используя способ деления многочлена на многочлен “уголком”.

8 этап работы. Домашнее задание.

Дома решить уравнения высших степеней, используя способ деления многочлена на многочлен “уголком” (раздать листы с заданиями).

Видео:Формула Кардано для решения кубических уравненийСкачать

Решение кубических уравнений

Кубическое уравнение, содержащее коэффициенты с действительным корнем, остальные два считаются комплексно-сопряженной парой. Будут рассмотрены уравнения с двучленами и возвратные, а также с поиском рациональных корней. Вся информация будет подкреплена примерами.

Видео:Решение уравнения методом замены переменнойСкачать

Решение двучленного кубического уравнения вида A x 3 + B = 0

Кубическое уравнение, содержащее двучлен, имеет вид A x 3 + B = 0 . Его необходимо приводить к x 3 + B A = 0 с помощью деления на А , отличного от нуля. После чего можно применять формулу сокращенного умножения суммы кубов. Получаем, что

x 3 + B A = 0 x + B A 3 x 2 — B A 3 x + B A 2 3 = 0

Результат первой скобки примет вид x = — B A 3 , а квадратный трехчлен — x 2 — B A 3 x + B A 2 3 , причем только с комплексными корнями.

Найти корни кубического уравнения 2 x 3 — 3 = 0 .

Решение

Необходимо найти х из уравнения. Запишем:

2 x 3 — 3 = 0 x 3 — 3 2 = 0

Необходимо применить формулу сокращенного умножения. Тогда получим, что

x 3 — 3 2 = 0 x — 3 3 2 6 x 2 + 3 3 2 6 x + 9 2 3 = 0

Раскроем первую скобку и получим x = 3 3 2 6 . Вторая скобка не имеет действительных корней, потому как дискриминант меньше нуля.

Ответ: x = 3 3 2 6 .

Видео:РЕШЕНИЕ КУБИЧЕСКОГО УРАВНЕНИЯ МЕТОДОМ ГРУППИРОВКИСкачать

Решение возвратного кубического уравнения вида A x 3 + B x 2 + B x + A = 0

Вид квадратного уравнения — A x 3 + B x 2 + B x + A = 0 , где значения А и В являются коэффициентами. Необходимо произвести группировку. Получим, что

A x 3 + B x 2 + B x + A = A x 3 + 1 + B x 2 + x = = A x + 1 x 2 — x + 1 + B x x + 1 = x + 1 A x 2 + x B — A + A

Корень уравнения равен х = — 1 , тогда для получения корней квадратного трехчлена A x 2 + x B — A + A необходимо задействовать через нахождение дискриминанта.

Решить уравнение вида 5 x 3 — 8 x 2 — 8 x + 5 = 0 .

Решение

Уравнение является возвратным. Необходимо произвести группировку. Получим, что

5 x 3 — 8 x 2 — 8 x + 5 = 5 x 3 + 1 — 8 x 2 + x = = 5 x + 1 x 2 — x + 1 — 8 x x + 1 = x + 1 5 x 2 — 5 x + 5 — 8 x = = x + 1 5 x 2 — 13 x + 5 = 0

Если х = — 1 является корнем уравнения, тогда необходимо найти корни заданного трехчлена 5 x 2 — 13 x + 5 :

5 x 2 — 13 x + 5 = 0 D = ( — 13 ) 2 — 4 · 5 · 5 = 69 x 1 = 13 + 69 2 · 5 = 13 10 + 69 10 x 2 = 13 — 69 2 · 5 = 13 10 — 69 10

Ответ:

x 1 = 13 10 + 69 10 x 2 = 13 10 — 69 10 x 3 = — 1

Видео:Самый простой способ решить кубическое уравнениеСкачать

Решение кубических уравнений с рациональными корнями

Если х = 0 , то он является корнем уравнения вида A x 3 + B x 2 + C x + D = 0 . При свободном члене D = 0 уравнение принимает вид A x 3 + B x 2 + C x = 0 . При вынесении х за скобки получим, что уравнение изменится. При решении через дискриминант или Виета оно примет вид x A x 2 + B x + C = 0 .

Найти корни заданного уравнения 3 x 3 + 4 x 2 + 2 x = 0 .

Решение

3 x 3 + 4 x 2 + 2 x = 0 x 3 x 2 + 4 x + 2 = 0

Х = 0 – это корень уравнения. Следует найти корни квадратного трехчлена вида 3 x 2 + 4 x + 2 . Для этого необходимо приравнять к нулю и продолжить решение при помощи дискриминанта. Получим, что

D = 4 2 — 4 · 3 · 2 = — 8 . Так как его значение отрицательное, то корней трехчлена нет.

Ответ: х = 0 .

Когда коэффициенты уравнения A x 3 + B x 2 + C x + D = 0 целые, то в ответе можно получить иррациональные корни. Если A ≠ 1 , тогда при умножении на A 2 обеих частей уравнения проводится замена переменных, то есть у = А х :

A x 3 + B x 2 + C x + D = 0 A 3 · x 3 + B · A 2 · x 2 + C · A · A · x + D · A 2 = 0 y = A · x ⇒ y 3 + B · y 2 + C · A · y + D · A 2

Приходим к виду кубического уравнения. Корни могут быть целыми или рациональными. Чтобы получить тождественное равенство, необходимо произвести подстановку делителей в полученное уравнение. Тогда полученный y 1 будет являться корнем. Значит и корнем исходного уравнения вида x 1 = y 1 A . Необходимо произвести деление многочлена A x 3 + B x 2 + C x + D на x — x 1 . Тогда сможем найти корни квадратного трехчлена.

Найти корни заданного уравнения 2 x 3 — 11 x 2 + 12 x + 9 = 0 .

Решение

Необходимо произвести преобразование с помощью умножения на 2 2 обеих частей, причем с заменой переменной типа у = 2 х . Получаем, что

2 x 3 — 11 x 2 + 12 x + 9 = 0 2 3 x 3 — 11 · 2 2 x 2 + 24 · 2 x + 36 = 0 y = 2 x ⇒ y 3 — 11 y 2 + 24 y + 36 = 0

Свободный член равняется 36 , тогда необходимо зафиксировать все его делители:

± 1 , ± 2 , ± 3 , ± 4 , ± 6 , ± 9 , ± 12 , ± 36

Необходимо произвести подстановку y 3 — 11 y 2 + 24 y + 36 = 0 , чтобы получить тождество вида

1 3 — 11 · 1 2 + 24 · 1 + 36 = 50 ≠ 0 ( — 1 ) 3 — 11 · ( — 1 ) 2 + 24 · ( — 1 ) + 36 = 0

Отсюда видим, что у = — 1 – это корень. Значит, x = y 2 = — 1 2 .

Далее следует деление 2 x 3 — 11 x 2 + 12 x + 9 на x + 1 2 при помощи схемы Горнера:

2 x 3 — 11 x 2 + 12 x + 9 = x + 1 2 2 x 2 — 12 x + 18 = = 2 x + 1 2 x 2 — 6 x + 9

После чего необходимо найти корни квадратного уравнения вида x 2 — 6 x + 9 . Имеем, что уравнение следует привести к виду x 2 — 6 x + 9 = x — 3 2 , где х = 3 будет его корнем.

Ответ: x 1 = — 1 2 , x 2 , 3 = 3 .

Алгоритм можно применять для возвратных уравнений. Видно, что — 1 – это его корень, значит, левая часть может быть поделена на х + 1 . Только тогда можно будет найти корни квадратного трехчлена. При отсутствии рациональных корней применяются другие способы решения для разложения многочлена на множители.

Видео:9 класс. Алгебра. Решение уравнений методом замены переменной.Скачать

Решение кубических уравнений по формуле Кардано

Нахождение кубических корней возможно при помощи формулы Кардано. При A 0 x 3 + A 1 x 2 + A 2 x + A 3 = 0 необходимо найти B 1 = A 1 A 0 , B 2 = A 2 A 0 , B 3 = A 3 A 0 .

После чего p = — B 1 2 3 + B 2 и q = 2 B 1 3 27 — B 1 B 2 3 + B 3 .

Полученные p и q в формулу Кардано. Получим, что

y = — q 2 + q 2 4 + p 3 27 3 + — q 2 — q 2 4 + p 3 27 3

Подбор кубических корней должен удовлетворять на выходе значению — p 3 . Тогда корни исходного уравнения x = y — B 1 3 . Рассмотрим решение предыдущего примера, используя формулу Кардано.

Найти корни заданного уравнения 2 x 3 — 11 x 2 + 12 x + 9 = 0 .

Решение

Видно, что A 0 = 2 , A 1 = — 11 , A 2 = 12 , A 3 = 9 .

Необходимо найти B 1 = A 1 A 0 = — 11 2 , B 2 = A 2 A 0 = 12 2 = 6 , B 3 = A 3 A 0 = 9 2 .

Отсюда следует, что

p = — B 1 2 3 + B 2 = — — 11 2 2 3 + 6 = — 121 12 + 6 = — 49 12 q = 2 B 1 3 27 — B 1 B 2 3 + B 3 = 2 · — 11 2 3 27 — — 11 2 · 6 3 + 9 2 = 343 108

Производим подстановку в формулу Кордано и получим

y = — q 2 + q 2 4 + p 3 27 3 + — q 2 — — q 2 4 + p 3 27 3 = = — 343 216 + 343 2 4 · 108 2 — 49 3 27 · 12 3 3 + — 343 216 — 343 2 4 · 108 2 — 49 3 27 · 12 3 3 = = — 343 216 3 + — 343 216 3

— 343 216 3 имеет три значения. Рассмотрим их ниже.

— 343 216 3 = 7 6 cos π + 2 π · k 3 + i · sin π + 2 π · k 3 , k = 0 , 1 , 2

Если k = 0 , тогда — 343 216 3 = 7 6 cos π 3 + i · sin π 3 = 7 6 1 2 + i · 3 2

Если k = 1 , тогда — 343 216 3 = 7 6 cosπ + i · sinπ = — 7 6

Если k = 2 , тогда — 343 216 3 = 7 6 cos 5 π 3 + i · sin 5 π 3 = 7 6 1 2 — i · 3 2

Необходимо произвести разбиение по парам, тогда получим — p 3 = 49 36 .

Тогда получим пары: 7 6 1 2 + i · 3 2 и 7 6 1 2 — i · 3 2 , — 7 6 и — 7 6 , 7 6 1 2 — i · 3 2 и 7 6 1 2 + i · 3 2 .

Преобразуем при помощи формулы Кордано:

y 1 = — 343 216 3 + — 343 216 3 = = 7 6 1 2 + i · 3 2 + 7 6 1 2 — i · 3 2 = 7 6 1 4 + 3 4 = 7 6 y 2 = — 343 216 3 + — 343 216 3 = — 7 6 + — 7 6 = — 14 6 y 3 = — 343 216 3 + — 343 216 3 = = 7 6 1 2 — i · 3 2 + 7 6 1 2 + i · 3 2 = 7 6 1 4 + 3 4 = 7 6

x 1 = y 1 — B 1 3 = 7 6 + 11 6 = 3 x 2 = y 2 — B 1 3 = — 14 6 + 11 6 = — 1 2 x 3 = y 3 — B 1 3 = 7 6 + 11 6 = 3

Ответ: x 1 = — 1 2 , x 2 , 3 = 3

При решении кубических уравнений можно встретить сведение к решению уравнений 4 степени методом Феррари.

🌟 Видео

Решение уравнения третьей степени x³-9x-12=0Скачать

Решение кубических уравненийСкачать

Решить кубическое уравнение. Два способаСкачать

Теорема БезуСкачать

Решение уравнений третьей степени (формула Кардано)Скачать

Как решать кубические уравнения Решите уравнение 3 степени 9 класс Разложить на множители ДелениеСкачать

решение уравнения с заменой переменнойСкачать

ОГЭ 2022. Кубическое уравнение. Метод группировки.Скачать

ФОРМУЛА КАРДАНО-ТАРТАЛЬЯ + РЕКЛАМА МФТИ!!!Скачать