Доброго времени суток! Сегодня мы поговорим о решении ОДУ (обыкновенных дифференциальных уравнений) в Matlab. Перед тем как мы начнём обсуждать данную тему, советую вам ознакомиться с темой: Численное дифференцирование в Matlab, чтобы лучше понимать теоретическую составляющую решения ОДУ.
- Обыкновенные дифференциальные уравнения
- Методы решения дифференциальных уравнений
- Метод Рунге-Кутта первого порядка
- Метод Рунге-Кутта второго порядка
- Метод Рунге-Кутта четвёртого порядка
- Решение ОДУ в Matlab стандартными средствами
- Решение краевой задачи с использованием MATLAB
- Численное решение краевых (граничных) задач
- Лабораторная работа Решение дифференциальных уравнений в Matlab
- 🌟 Видео
Обыкновенные дифференциальные уравнения
С помощью дифференциальных уравнений можно описать разные задачи: движения системы, взаимодействующих материальных точек, химической кинетики и т.д. Различают три типа задач для систем диф. уравнений:
- Задача Коши
- Краевая задача
- Задача на собственные значения
Кратко расскажу о их сути:
Задача Коши предполагает дополнительные условия в виде значения функции в определённой точке.
Краевая задача подразумевает поиск решения на заданном отрезке с краевыми (граничными) условиями в концах интервала или на границе области.
Задача на собственные значения — помимо искомых функций и их производных, в уравнение входят дополнительное несколько неизвестных параметров, которые являются собственными значениями.
Видео:MatLab. Решение дифференциального уравнения.Скачать

Методы решения дифференциальных уравнений
Решение ОДУ в Matlab и не только, в первую очередь, сводится к выбору порядка численного метода решения. Порядок численного метода не связан с порядком дифференциального уравнения. Высокий порядок у численного метода означает его скорость сходимости.
В случае большого интервала, с помощью алгоритмов с низким порядком сжимают интервал с решениями и находят приблизительные корни, а затем уже уточняют корни с помощью методов с высоким порядком.
Решение обыкновенных дифференциальных уравнений в Matlab можно реализовать «своими ручками», прописав алгоритм по разным схемам. Но также в Matlab есть встроенные функции, выполняющие все стандартные задачи.
Метод Рунге-Кутта первого порядка
Методы Рунге-Кутта представляют собой разложения в ряд Тейлора и от количества использованных элементов ряда зависит порядок этого метода. Следовательно, помимо Рунге-Кутта первого порядка, вы сможете увидеть методы других порядков. Иногда их называют другими именами.
Например, Метод Рунге-Кутта первого порядка, также известен как Метод Эйлера или Метод ломаных. Информацию о его математическом и графическом представлении советую поискать в гугл. Мы же поговорим о том, как Метод Рунге-Кутта первого порядка реализуется в Matlab для решения ОДУ. Например:
Решить и привести график ошибки уравнения y’ = y*x методом Рунге-Кутта первого порядка (Методом Эйлера, Методом ломаных).
Погрешность Метода Рунге-Кутта 1 порядка
» data-medium-file=»https://i2.wp.com/codetown.ru/wp-content/uploads/2017/02/Рунге-1-погрешность.png?fit=300%2C236&ssl=1″ data-large-file=»https://i2.wp.com/codetown.ru/wp-content/uploads/2017/02/Рунге-1-погрешность.png?fit=622%2C489&ssl=1″ loading=»lazy» src=»https://i2.wp.com/codetown.ru/wp-content/uploads/2017/02/%D0%A0%D1%83%D0%BD%D0%B3%D0%B5-1-%D0%BF%D0%BE%D0%B3%D1%80%D0%B5%D1%88%D0%BD%D0%BE%D1%81%D1%82%D1%8C.png?resize=622%2C489″ alt=»Погрешность метода 1 порядка» width=»622″ height=»489″ srcset=»https://i2.wp.com/codetown.ru/wp-content/uploads/2017/02/Рунге-1-погрешность.png?w=629&ssl=1 629w, https://i2.wp.com/codetown.ru/wp-content/uploads/2017/02/Рунге-1-погрешность.png?resize=300%2C236&ssl=1 300w» sizes=»(max-width: 622px) 100vw, 622px» data-recalc-dims=»1″ />
На данном графике показана зависимость величины ошибки от шага.
Метод Рунге-Кутта второго порядка
Также известен как Метод Эйлера-Коши. Как видите, во второй части уравнения происходит обращения к следующему шагу. Но как тогда быть, если нам ещё не известен следующий шаг? Всё просто. Метод Рунге-Кутта второго порядка — это всё тот же метод первого порядка, однако, на половине шага происходит нахождение «первичного» решения, а затем происходит его уточнение. Это позволяет поднять порядок скорости сходимости до двух.
Решить и привести график ошибки уравнения u’ = u*x методом Рунге-Кутта второго порядка.

По сравнению с Рунге-Куттом первого порядка изначальная ошибка уже гораздо меньше.
Мы не будем говорить о третьем порядке, потому что задачи на третий порядок встречаются редко, но если будет необходимо, пишите в комментариях, выложу.
Метод Рунге-Кутта четвёртого порядка
Метод Рунге-Кутта четвёртого порядка считается самым распространённым. Тем не менее, работает он аналогично второму и третьему порядку.
Решить и привести график ошибки уравнения u’ = u*x методом Рунге-Кутта четвёртого порядка.

Как видите, на последней картинке размерность ошибки на столько мала, что пришлось воспользоваться loglog() для лучшей видимости.
Решение ОДУ в Matlab стандартными средствами
Стоит отметить, что мы с вами разобрали только один самый известный метод решения ОДУ с разными порядками. Однако, методов очень много.
Для решения дифференциальных уравнений и систем в MATLAB предусмотрены следующие функции:
ode45 (f, interval, X0, [options])
ode23 (f, interval, X0, [options])
ode113 (f, interval, X0, [options])
ode15s (f, interval, X0, [options])
ode23s (f, interval, X0, [options])
ode23t (f, interval, X0, [options])
ode23tb (f, interval, X0, [options])
Входными параметрами этих функций являются:
- f — вектор-функция для вычисления правой части уравнения системы уравнений;
- interval — массив из двух чисел, определяющий интервал интегрирования дифференциального уравнения или системы;
- Х0 — вектор начальных условий системы дифференциальных уравнений;
- options — параметры управления ходом решения дифференциального уравнения или системы.
Все функции возвращают:
- массив Т — координаты узлов сетки, в которых ищется решение;
- матрицу X, i-й столбец которой является значением вектор-функции решения в узле Тi.
В функции ode45 реализован метод Рунге-Кутта 4-5 порядка точности, в функции ode23 также реализован метод Рунге-Кутта, но 2-3 порядка, а функция ode113 реализует метод Адамса.
Для решения жёстких систем предназначены функция ode15s, в которой реализован метод Гира, и функция ode23s, реализующая метод Розенброка. Для получения более точного решения жёсткой системы лучше использовать функцию ode15s. Для решения системы с небольшим числом жёсткости можно использовать функцию ode23t, а для грубой оценки подобных систем служит функция ode23tb.
Символьное решение обыкновенных дифференциальных уравнений произвольного порядка осуществляет функция dsolve r = dsolve(‘eq1,eq2,…’, ‘cond1,cond2,…‘, ‘v’)
Пример использования:
На этом мы закончим. Если остались вопросы, задавайте их в комментариях. Также вы можете скачать исходники чтобы лучше понять тему: «Решение ОДУ в Matlab».
Видео:Решение систем Д/У: 1. Знакомство с функциями odeXYСкачать

Решение краевой задачи с использованием MATLAB
Решение краевой задачи на примере обыкновенных дифференциальных уравнений второго порядка с использованием MATLAB
функция граничный солвер дифференциальный
Данный вид уравнения представляет собой ОДУ второго порядка
и граничными условиями
б • y (a) + в ? y'(a) = A, г • y(b) + д ? y'(b) = B,
где х, y — координаты;
б, в, г, д, A, B — заданные числа.
Решение этой задачи в MATLAB состоит из следующих этапов:
- 1) преобразование дифференциального уравнения второго порядка к системе двух уравнений первого порядка;
- 2) написание функции для вычисления правой части системы;
- 3) написание функции, определяющей граничные условия;
- 4) формирование начального приближения при помощи специальной функции bvpinit;
- 5) вызов солвера bvp4c для решения граничной задачи;
- 6) визуализация результата.
- 1) Для решения ОДУ второго порядка введем две вспомогательные функции, количество которых определяется порядком уравнения.
Составим систему уравнений первого порядка
y2′ = y2/x — 2/x2; y2(0,5) 2
2) Функция правой части системы зависит от x и вектора y, состоящего из двух компонентов, y(1) соответствует y1, а y(2) — y2.
Функция должна иметь два входных аргумента: переменную x, по которой производится дифференцирование, и вектор, размер которого равен числу неизвестных функций системы. Выходным аргументом функции является вектор правой части системы.
Можно использовать функции вычисления вектора правых частей (twoode.m) и соблюдения граничных условий (twobc.m).
3) При постановке граничных условий для вспомогательных функций требуется преобразовать их так, чтобы в правых частях стояли нули. Функция, описывающая граничные условия, зависит от двух аргументов — векторов ya и yb.
В данной задаче ya(2)-2=0, yb(1)-0=0
4) Для задания начальной сетки и приближения предназначена функция bvpinit, обращение к которой в самом простом случае выглядит следующим образом:
bvpinit (начальная сетка, начальное приближение к решению).
Начальная сетка определяется вектором координат узлов, упорядоченных по возрастанию и принадлежащих отрезку [a,b]. Формирование равномерной сетки целесообразно производить функцией linspace:
возвращающей вектор х из n равноотстоящих узлов между a и b, включая границы.
Заданная сетка модифицируется солвером в процессе решения для обеспечения требуемой точности. Постоянное начальное приближение задается вектором из двух элементов для функций y1 (х), y2 (х).
- 5) Солвер bvp4c основан на методе конечных разностей, т.е получающееся решение есть векторы значений неизвестных функций в точках отрезка (в узлах сетки). Выбор начальной сетки и приближения может оказать влияние на решение.
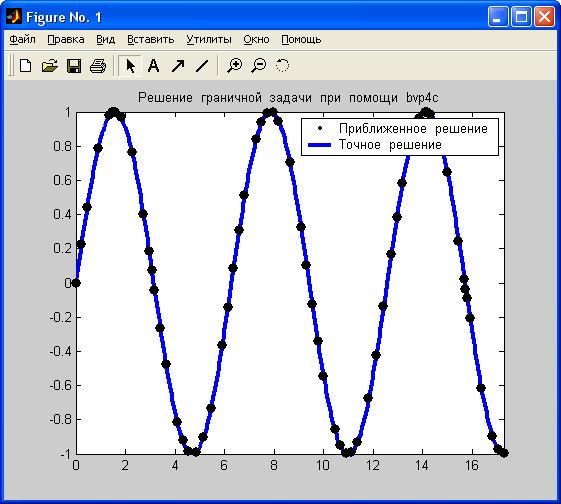
- 6) Отображаем графически приближенное решение, извлекая нужные компоненты из структуры, возвращаемой солвером (рис.1).
Листинг. Файл-функция для решения граничной задачи
Видео:Численное решение системы дифференциальных уравнений(задачи Коши)Скачать

Численное решение краевых (граничных) задач
Дата добавления: 2014-11-28 ; просмотров: 1782 ; Нарушение авторских прав
Для решения краевых задач, т.е. дифференциальных уравнений произвольного порядка n, или систем из n уравнений первого порядка вида 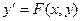
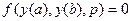
Точность решения контролируется при помощи двух опций управляющей структуры RelTol – для относительной точности и AbsTol – для абсолютной. Сама управляющая структура генерируется функцией bvpset
Opsions = bvpset (‘RelTol‘, 1.0e-05, ‘AbsTol’, 1.0e-07)
и задается в качестве четвертого входного аргумента солвера bvp4c.
Рассмотрим решение краевых задач на примере обыкновенного дифференциального уравнения второго порядка (n=2). Требуется найти функцию у(х), удовлетворяющую на отрезке [a, b] дифференциальному уравнению и граничными условиями:
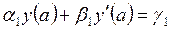
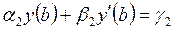
где 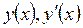
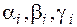
Решение этой задачи состоит из следующих этапов:
1. Преобразование дифференциального уравнения второго порядка к системе двух уравнений первого порядка.
2. Написание функции для вычисления правой части системы.
3. Написание функции, определяющей граничные условия.
4. Формирование начального приближения при помощи специальной функции bvpinit.
5. Вызов солвера bvp4c для решения граничной задачи.
6. Визуализация результата.
Этап 1. Введение вспомогательных функций y1(x)=y и y2(x)=y1¢=y¢, приводит к системе из двух уравнений первого порядка относительно них (при постановке граничных условий для вспомогательных функций требуется преобразовать их так, чтобы в правых частях стояли нули):
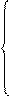
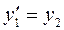
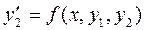
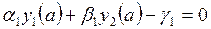
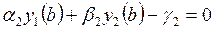
Этап 2. Функция правой части системы зависит от х и вектора у, состоящего из двух компонент, у(1) соответствует 
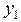
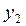
Этап 3. Функция, описывающая граничные условия, зависит от двух аргументов векторов ya и yb и имеет следующую структуру:
function g = bound(ya,yb)
g = [alpha1*ya(1)+beta1*ya(2)–gamma1; alpha2*yb(1)+beta2*yb(2) –gamma2];
причем вместо alpha1, beta1, gamma1, alpha2, beta2, gamma2 следует подставить заданные числа.
Этап 4. Солвер bvp4c основан на методе конечных разностей, т. е. получающееся решение есть векторы значений неизвестных функций в точках отрезка (в узлах сетки). Выбор начальной сетки и приближение может оказать влияние на решение, выдаваемое солвером bvp4c. Для задания начальной сетки и приближения предназначена функция bvpinit, обращение к которой в самом простом случае выглядит в виде
initsol = bvpinit (начальная сетка, начальное приближение к решению),
где начальная сетка определяется вектором координат узлов, упорядоченных по возрастанию и принадлежащих отрезку [a, b]. Если имеется априорная информация о решении, то разумно среди точек начальной сетки указать те, в которых решение сильно изменяется.
Формирование равномерной сетки целесообразно производить функцией linspace,которая возвращает вектор х из n равноотстоящих узлов между a и b, включая границы:
X = linspace (a, b, n).
Заданная сетка модифицируется солвером в процессе решения для обеспечения требуемой точности. Постоянное начальное приближение задается вектором из двух элементов функций 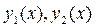
1) требуется запрограммировать функцию, которая по заданному х возвращает вектор из двух компонент со значениями 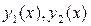
2) поместить указатель на нее во втором входном аргументе bvpinit. В результате работы bvpinit генерируется структура initsol с информацией о начальном приближении.
Этап 5. После определения начального приближения вызывается солвер bvp4c, входными аргументами которого являются указатели на функции правой части системы и граничных условий, начальное приближение и, при необходимости, управляющая структура с параметрами вычислительного процесса. Управляющая структура формируется при помощи функции bvpset. Солвер bvp4c возвращает единственный выходной аргумент – структуру с информацией о расчетной сетке, значения искомой функции и ее производной. Солвер bvp4c так же, как и и солвер dde23 для ДУ с запаздыванием, позволяет получить результат только в виде структуры.
Для вычисления значений приближенного решения в произвольных точках отрезка следует применить функцию deval, так же как и в случае решения задачи Коши.
Рассмотрим решение граничной задачи при помощи bvp4c для дифференциального уравнения второго порядка:
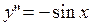
После преобразования получаем следующую систему ДУ первого порядка (этап 1)
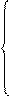
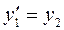
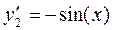
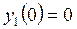
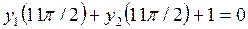
Подготовим функцию по имени rside для правых частей системы ДУ в виде m-файла (этап 2).
function f = rside(x, y)
Подготовим функцию по имени bound дл я граничных условий в виде m-файла (этап 3).
function f = bound(ya, yb)
f = [ya(1); yb(1) + yb(2) + 1];
При помощи bvpinit зададим начальную сетку на отрезке [0, 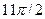
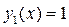
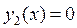
% формирование начальной сетки meshinit и начального приближения yinit
»meshinit = linspace(0, 11*pi/2, 20);
»initsol = bvpinit(meshinit, yinit);
Вызовем солвер bvp4c и получим приближенное решение.
»sol = bvp4c(@rside, @bound, initsol);
Отобразим графически приближенное решение, извлекая нужные компоненты из структуры возвращаемой солвером, т.е. используем поля x и y структуры sol для построения решения:
% в sol.x содержатся координаты сетки
% в sol.y(1, 🙂 соответствует значениям функции y1 в sol.x(:)
% в sol.y(2, 🙂 соответствует значениям функции y2 в sol.x(:)
Отобразим графически точное решение 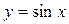
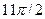
»fplot(@sin, [0 11*pi/2]);
»title(‘Решение граничной задачи при помощи bvp4c’);
»legend(‘Приближенное решение’, ‘Точное решение’);
Как следует из полученных графиков (в виде точек и сплошной линии) для простых задач солвер bvp4c дает хорошие результаты. По умолчанию решение найдено с относительной точностью 10 -3 и относительной 10 -6 по невязке.
Приложение 4
| | | следующая лекция ==> | |
| Численное решение ОДУ и их систем | | | Алгебраических уравнений |
Не нашли то, что искали? Google вам в помощь!
Видео:Математика это не ИсламСкачать

Лабораторная работа Решение дифференциальных уравнений в Matlab
| Название | Лабораторная работа Решение дифференциальных уравнений в Matlab |
| Дата | 15.02.2018 |
| Размер | 0.51 Mb. |
| Формат файла |  |
| Имя файла | lab#5DiffEquationsMatlab.docx |
| Тип | Лабораторная работа #36539 |
| Подборка по базе: Расчетная работа1.docx, ВЫПУСКНАЯ КВАЛИФИКАЦИОННАЯ РАБОТА. Тема_ «Модернизация компьютер, Практическая работа Иванова 28.04.21.docx, Практическая работа 4docx.docx, практическая работа 2.docx, Практическая работа 8.doc, Самостоятельная работа по теме 4.3.docx, Практическая работа 4.docx, Практическая работа 1_1 2 кл (1) (1) (1).docx, практическая работа 4.docx РОССИЙСКИЙ УНИВЕРСИТЕТ ТРАНСПОРТА (МИИТ) Кафедра «Управление и защита информации» «Решение дифференциальных уравнений в Matlab» «ИСТОРИЯ И МЕТОДОЛОГИЯ НАУКИ И ТЕХНИКИ В ОБЛАСТИ УПРАВЛЕНИЯ» Выполнила: студентка группы ТУУ-151 Проверила: доц. Зольникова Н.Н. Решить дифференциальное уравнение: при начальном условии Решим данную задачу Коши с помощью метода Рунге-Кутта 4-5 порядка точности, используя функцию ode45(). Для этого запишем исходное уравнение как функцию в Matlab: function y = dy( x, y ) %Уравнение, задающее производную y = 2*cos(2*x) + sin(y); end interval = [0, 50]; [X,Y] = ode45(@dy, interval, y0); plot(X, Y) %изображение графика функции grid on %создание сетки на графике Решить задачу Коши и краевую задачу для дифференциального уравнения Для нахождения решения данного дифференциального уравнения следует найти общее решение соответствующего однородного дифференциального уравнения Составляем и решаем характеристическое уравнение: Характеристическое уравнение имеет два кратных действительных корня, следовательно, общее решение однородного уравнения имеет вид: Найдем частное решение. Так как в исходном уравнении правая часть представляет собой константу, то частное решение будет иметь вид: Подставляем частное решение в исходное уравнение. Получаем: Таким образом, частное решение имеет вид: Общее решение исходного дифференциального уравнения записывается в виде: При этом производная Решение задачи Коши. Для нахождения Таким образом, при данных начальных условиях получаем решение в виде: Решение краевой задачи. Для определения Таким образом, при данных краевых условиях получаем решение в виде: Решим задачу Коши аналитически с помощью метода dsolve() и методом Рунге-Кутта с помощью функции ode45(). В функцию dsolve() необходимо записать исходное уравнение, начальные или граничные условия и переменную, по которой происходит дифференцирование. Символ «Dy» обозначает первую производную, «D2y» соответственно вторую производную. Y = dsolve(‘D2y+2*Dy+y=1.5’, ‘y(0)=0’, ‘Dy(0)=0’, ‘x’) y = ezplot(Y, [0,20]) %изображение графика символьного выражения set(y, ‘LineWidth’, 2); %установка толщины линии axis([0 20 0 2]); %задание границ графика grid on; %создание сетки на графике hold on; %следующий график будет рисоваться в этом же окне function F = dy2( x, y ) % ОДУ первого порядка %Решение с помощью метода Рунге-Кутта 4-5 порядка точности %Интервал, на которм будет находится решение [X,Y] = ode45(@dy2, interval, y0); %Значения искомой функции находятся в первом столбце матрицы Y plot(X, Y(:,1), ‘:r’, ‘LineWidth’, 1.5) %изображение графика функции legend(‘Аналитическое решение’,’Метод Рунге-Кутта’); Решение краевой задачи также найдем аналитически через функцию dsolve() и с помощью методов bvp4c() и ode45(). Y = dsolve(‘D2y+2*Dy+y=1.5’, ‘y(0)= 1’, ‘Dy(5)=6.5’, ‘x’) y = ezplot(Y, [0,20]); %изображение графика символьного выражения set(y, ‘LineWidth’, 2); %установка толщины линии axis([0 20 -100 50]); %задание границ графика grid on; %создание сетки на графике hold on; %следующий график будет рисоваться в этом же окне
function res = boundCon( ya, yb ) %Функция, вычисляющая разность между значением в граничной точке % и точным значением %Задаем стартовые значения для поиска начальных условий solinit = bvpinit(linspace(0,5), [1 1]); %Нахождение значений y(x) и y'(x) на интервале [0;5] sol = bvp4c(@dy2, @boundCon, solinit); [X,Y] = ode45(@dy2, interval, y0); %Значения искомой функции находятся в первом столбце матрицы Y plot(X, Y(:,1), ‘:r’, ‘LineWidth’, 1.5) %изображение графика функции legend(‘Аналитическое решение’,’Метод Рунге-Кутта’); Графики решений полностью совпали. Изобразим фазовый портрет системы. Для этого решим ее с помощью функции ode45() при различных начальных условиях. %Интервал, на которм будет находится решение [X,Y] = ode45(@dy2, interval, y0); %Значения функции y(x) находятся в первом столбце %Значения производной y'(x) находятся во втором столбце 🌟 ВидеоЗадача Коши ➜ Частное решение линейного однородного дифференциального уравненияСкачать  Численное решение дифференциальных уравнений (задачи Коши)Скачать  Как в MATLAB Simulink моделировать уравнения (Структурная схема САУ)Скачать  Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентамиСкачать  Решение дифференциальных уравнений и систем. Урок 150Скачать  5 Численное решение дифференциальных уравнений Part 1Скачать  5 Численное решение дифференциальных уравнений Part 1Скачать  Метод ЭйлераСкачать  Методы решения нелинейных краевых задач для ОДУСкачать  Работа в MATLAB. МКР. Задача КошиСкачать  MatLab. 7.9. Системы дифференциальных уравненийСкачать  7. Линейные дифференциальные уравнения первого порядка. Метод Бернулли.Скачать  ТАУ. Matlab/SIMULINK Фазовые портреты систем нелинейных диф. уравненийСкачать  Решение систем Д/У: 2. Опции решателей odeXYСкачать  |

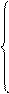
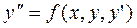
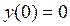
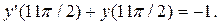

















 и
и  подставим начальные условия и решим систему:
подставим начальные условия и решим систему:








